Действия над матрицами (примеры). 1) Сумма (разность) матриц
 Скачать 96.42 Kb.
|
|
Действия над матрицами (примеры). 1) Сумма (разность) матриц: НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ. Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой! 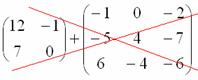 Пример: Сложить матрицы  и  Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:  Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов. Пример: Найти разность матриц 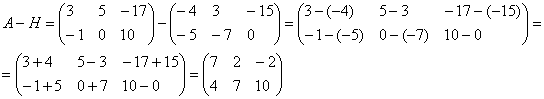 ,   2) Умножение матрицы на число. Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. Пример:   3) Транспонирование матрицы. Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы. Пример: Транспонировать матрицу  Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:  – транспонированная матрица.Транспонированная матрица обычно обозначается надстрочным индексом  . Пошаговый пример:Транспонировать матрицу 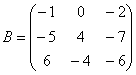 Сначала переписываем первую строку в первый столбец:  Потом переписываем вторую строку во второй столбец: 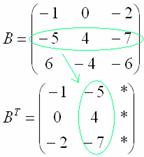 И, наконец, переписываем третью строку в третий столбец: 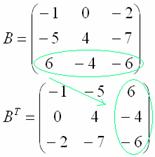 4) Умножение матриц. Какие матрицы можно умножать? Чтобы матрицу  можно было умножить на матрицу  нужно, чтобы число строк матрицы равнялось числу столбцов матрицы .Пример 1: Можно ли умножить матрицу  на матрицу  ?  , значит, умножать данные матрицы можно.А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!   , следовательно, выполнить умножение невозможно:  (Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.) Умножить матрицу  на матрицу  Пример 2: Умножить матрицу  на матрицу   В результате получена так называемая нулевая матрица. Попробуйте самостоятельно выполнить умножение  (правильный ответ  ).Обратите внимание, что  ! Это почти всегда так!Таким образом, при умножении переставлять матрицы нельзя! Если в задании предложено умножить матрицу  на матрицу  , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.Пример 3: Переходим к матрицам третьего порядка: Умножить 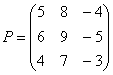матрицу  на матрицу 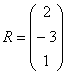  А теперь попробуйте самостоятельно разобраться в умножении следующих матриц: Пример 4: Умножьте матрицу 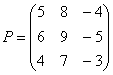на матрицу  Вот готовое решение, но постарайтесь сначала в него не заглядывать!  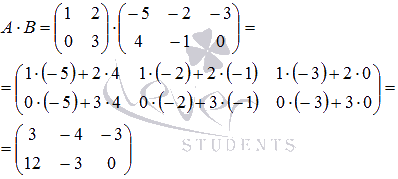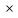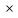Пример 5:  Пример 6: Так как порядок матрицы А равен 3  1, а матрицы В равен 1 3, то А В будет иметь порядок 3 на 3, а произведение матриц В A будет иметь порядок 1 на 1. 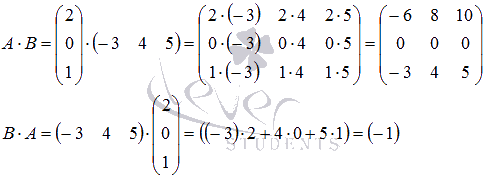Пример 7: Даны матрицы: 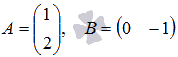 Выполните с заданными матрицами указанные действия:  Решение: Начинаем с умножения матрицы А на матрицу В: 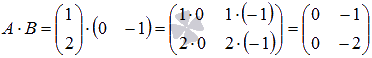 Теперь умножаем единичную матрицу второго порядка Е на два:  Складываем две полученные матрицы:  Осталось выполнить операцию умножения полученной матрицы на матрицу А: 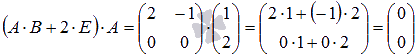 Пример 8: Даны матрицы:   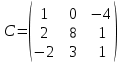 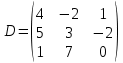 Вычислить  .Решение: Важно помнить про ПОРЯДОК ДЕЙСТВИЙ! 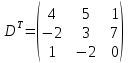 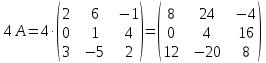    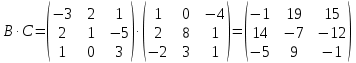   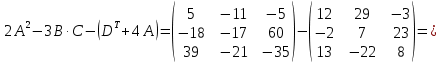  |