Кр. Курсовая работа. Департамент образования и науки города москвы государственное бюджетное профессиональное образовательное учреждение города Москвы
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
Нагрузки от действия центробежной силыЦентробежная сила элементарного участка лопатки протяженностью dr(рис. 3), выражается формулой: 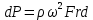 (1) (1)где ρ - плотность материала; ω - угловая скорость колеса; F - площадь поперечного сечения лопатки на радиусе r. 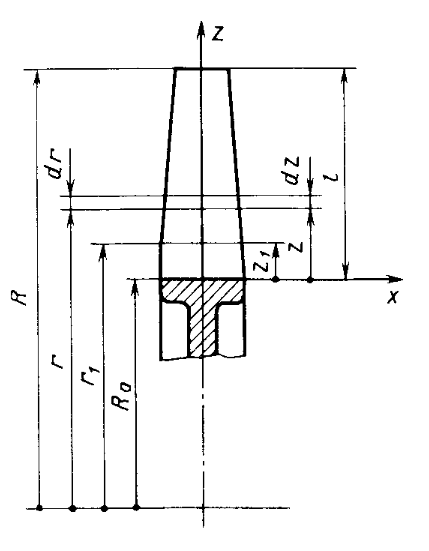 Рис. 3. К расчету лопатки на растяжение Центробежная сила, действующая в сечении на радиусе r1, равна интегралу: 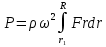 (2) (2)а напряжение растяжения: 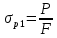 (3) (3) Площадь F поперечного сечения лопатки изменяется по ее длине по сложному закону. Формируя геометрию пера лопатки по выше перечисленным требованиям, невозможно и нет смысла вписать закон изменения площадей в какое-либо математическое выражение. Поэтому вычисление интеграла (2) и напряжения растяжения (3) производится численными методами. Для того чтобы оценить характер распределения напряжений растяжения по длине лопатки, можно принять некоторый осредненный закон распределения площадей. Площадь F поперечного сечения лопатки изменяется по ее длине по сложному закону. Формируя геометрию пера лопатки по вышеперечисленным требованиям, невозможно и нет смысла вписать закон изменения площадей в какое-либо математическое выражение. Поэтому вычисление интеграла (2) и напряжения растяжения (3) производится численными методами. Для того чтобы оценить характер распределения напряжений растяжения по длине лопатки, можно принять некоторый осредненный закон распределения площадей: 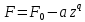 (4) (4)где F0 - площадь поперечного сечения лопатки в корневом сечении; q - показатель, определяющий степень изменения площадей по длине лопатки; a - коэффициент, зависящий от соотношения площадей на конце лопатки и в корневом сечении. Согласно формуле (4) он равен 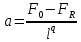 (5) (5)Для лопаток постоянного сечения a = 0 независимо от q. На рис. 4 показаны распределения площадей при различных значениях q. 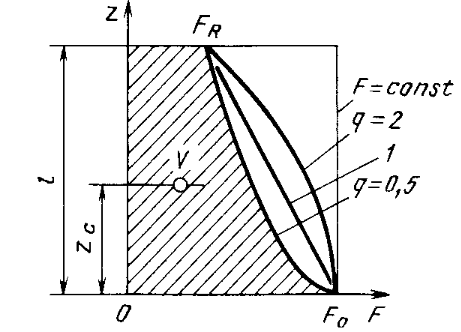 Рис. 4. Распределение площадей поперечных сечений вдоль пера При q > 0 поперечное сечение лопатки изменяется по параболическому закону, а при q < 0 - по гиперболическому. При q = 1 имеет линейный закон изменения площадей. Масса лопатки вычисляется по формуле: 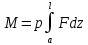 (6) (6)Нетрудно видеть, что площадь, лежащая слева от соответствующей кривой, представляет собой объем пера лопатки и пропорциональна его массе. Положение центра тяжести этой площади 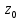 определяет положение центра массы лопатки относительно корневого сечения. определяет положение центра массы лопатки относительно корневого сечения.По рис. 4 видно, что наиболее легкой получается лопатка при 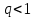 , а наиболее тяжелой при , а наиболее тяжелой при 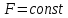 . .Подставив в формулу (6) формулу (4) и вычислив интеграл, можно получить оценку масс лопаток при различных 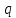 и и 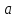 в сравнении с лопаткой постоянного сечения. в сравнении с лопаткой постоянного сечения.Получим формулу 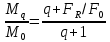 (7) (7)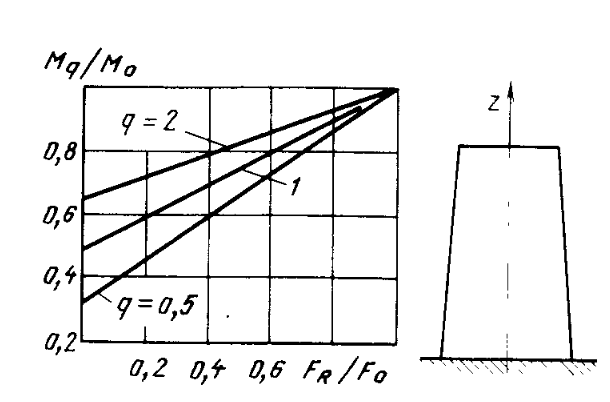 Рис. 5. Отношение массы пера к массе пера постоянного поперечного сечения На рис.5 показано соотношение масс лопаток, построенное по формуле (7). Оно показывает, что за счет профилирования сечений лопатки по ее длине масса уменьшается почти в два раза. Это позволяет уменьшить центробежную силу лопатки, напряжения растяжения и увеличить окружную скорость рабочего колеса. Формулу для расчета растягивающей инерционной силы, действующей в сечении лопатки с координатой 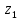 получим из (2), подставив в нее функцию площади (4) и заменив получим из (2), подставив в нее функцию площади (4) и заменив 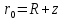 : :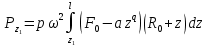 Интегрируя выражение, имеем 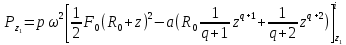 (8) (8)Напряжение растяжения в сечении будет равно 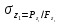 (9) (9)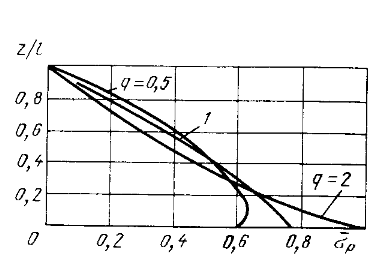 Рис. 6. Относительное распределение напряжений растяжения вдоль пера лопатки при различных законах профилирования пера Наиболее благоприятное распределение напряжений получается при 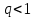 . Однако нецелесообразно занижать напряжения в корневом сечении и перемещать максимум в среднюю зону лопатки, особенно для турбинных лопаток, у которых температура корневой части лопатки ниже и прочность материала выше. Практически рационально профилировать лопатку по значениям . Однако нецелесообразно занижать напряжения в корневом сечении и перемещать максимум в среднюю зону лопатки, особенно для турбинных лопаток, у которых температура корневой части лопатки ниже и прочность материала выше. Практически рационально профилировать лопатку по значениям 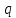 , лежащим в пределах 0,7…1,0. Профилированные по длине лопатки позволяют снизить напряжения растяжения в корневой части лопатки на 30…35% по сравнению с лопаткой постоянного сечения. , лежащим в пределах 0,7…1,0. Профилированные по длине лопатки позволяют снизить напряжения растяжения в корневой части лопатки на 30…35% по сравнению с лопаткой постоянного сечения.Если лопатки имеют бандажную полку, то напряжения растяжения, создаваемые бандажной полкой, складываются с напряжениями от собственной массы лопатки. Напряжения от бандажной полки определяются по формуле: 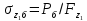 (10) (10)где 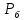 – центробежная сила бандажной полки – величина постоянная для всех сечений лопатки, лежащих ниже бандажной полки: – центробежная сила бандажной полки – величина постоянная для всех сечений лопатки, лежащих ниже бандажной полки: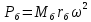 (11) (11)Здесь 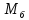 - масса бандажной полки; - масса бандажной полки; 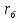 – радиус расположения ее центра инерции сечения. – радиус расположения ее центра инерции сечения.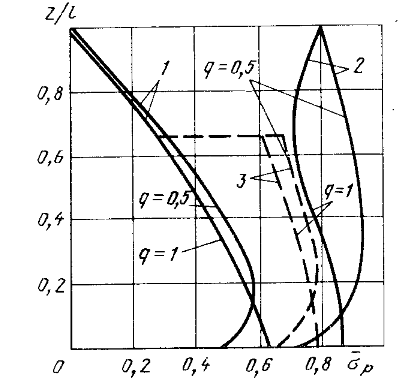 Рис. 7. Расположение напряжений в лопатках с бандажной полкой: 1 – напряжения при отсутствия бандажной полки (1) с концевой бандажной полкой (2) со срединной полкой (3) На рис. 7 показано распределение напряжений в лопатке с бандажной полкой и без нее при различных законах профилирования. Характеристики построены для 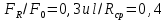 Ввиду того, что площади поперечного сечения лопатки в направлении от корневого сечения к ее концу уменьшаются, напряжения от действия бандажной полки растут. Это выравнивает напряжения, и наиболее рациональный закон профилирования лопатки становится близким к 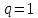 . .Напряжения растяжения для лопаток являются основными. Они составляют в среднем 50…70% общего напряжения. При этом, что очень важно, они действуют по всему сечению лопатки, но не в отдельных точках. Поэтому приближенная оценка лопатки часто производится по напряжениям растяжения, с последующим уточнением, полным расчетом. Величина напряжений растяжения в лопатках достигает следующих величин: для лопаток компрессоров из алюминиевого сплава – 150…200 МПа; титановых сплавов – 200…300 Мпа; стальных сплавов - 300…400 МПа. |
