Изгибающие моменты определяются на основании треугольника скоростей и статических давлений перед и за рабочим колесом в проекциях на координатные оси 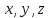 . . Примем правую систему осей координат (рис. 8).
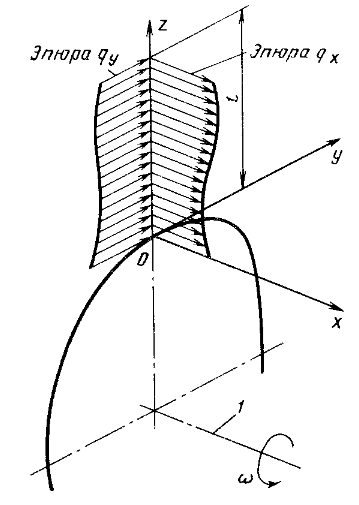 Рис.8. К расчету лопатки на изгиб: – ось ротора
Начало координат помещается в центр инерции корневого сечения. Ось x направлена параллельно оси ротора в сторону осевой скорости воздуха, ось y – в сторону, противоположную окружной скорости касательно к окружности корневых сечений лопаток. Ось z является радиальной осью. Методика определения изгибающих моментов является общей для компрессоров и турбин. В практических расчетах отличие состоит в знаках и величинах определяющих скоростей, давлений и получаемых моментов. Интенсивность давления на лопатку аэродинамических сил в проекциях на координатные плоскости обозначим 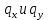 . Она определяется формулами . Она определяется формулами
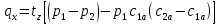 ; (12) ; (12) 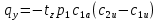 , (13) , (13)
где 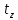 – шаг лопатки по окружности с координатой z, равный – шаг лопатки по окружности с координатой z, равный 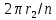 ; n – число лопаток; p, ; n – число лопаток; p, 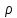 , , 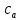 , , 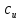 – статическое давление, плотность газа, осевые и окружные скорости за и перед рабочим колесом соответственно треугольникам скоростей; – статическое давление, плотность газа, осевые и окружные скорости за и перед рабочим колесом соответственно треугольникам скоростей; 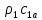 – массовый расход рабочего тела через лопаточную машину, отнесенную к единице проходного сечения. Первый член в формуле (12) представляет собой разность статических давлений на участок лопатки, разный единице. Второй член – сила реакции, равная изменению количества движения воздуха или газа под действием лопаток. В направлении оси – массовый расход рабочего тела через лопаточную машину, отнесенную к единице проходного сечения. Первый член в формуле (12) представляет собой разность статических давлений на участок лопатки, разный единице. Второй член – сила реакции, равная изменению количества движения воздуха или газа под действием лопаток. В направлении оси 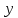 интенсивность интенсивность 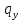 определяется только изменением количества движения. Для компрессора изменения осевых скоростей незначительно, поэтому интенсивность определяется только изменением количества движения. Для компрессора изменения осевых скоростей незначительно, поэтому интенсивность 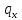 определяется разностью статических давлений и имеет отрицательный знак. Интенсивность определяется разностью статических давлений и имеет отрицательный знак. Интенсивность 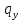 положительная, так как лопатки компрессора создают закрутку воздуху и положительная, так как лопатки компрессора создают закрутку воздуху и 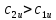 . Для турбины . Для турбины 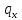 имеет положительный знак, так как имеет положительный знак, так как 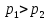 , а , а 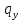 – отрицательный, так как – отрицательный, так как 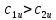 . . Выделим на лопатке элементарный участок протяженностью dz (рис. 9)
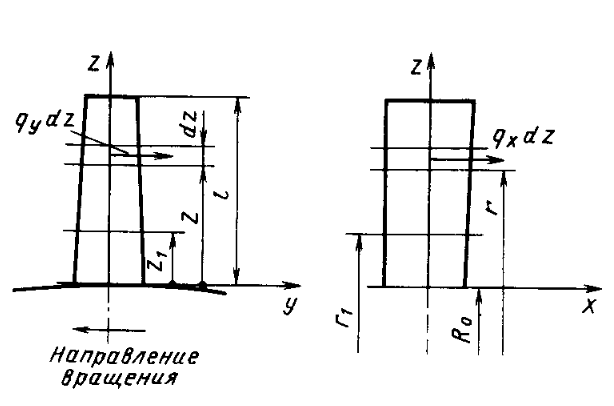
Рис. 9. К расчету лопатки на изгиб газодинамическими силами
Компоненты газодинамических сил, действующие на элементарный участок, равны 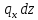 и и 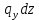 . Элементарные моменты, создаваемые этими силами в сечении с координатой . Элементарные моменты, создаваемые этими силами в сечении с координатой 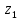 , определяются формулами , определяются формулами |
 Скачать 1.2 Mb.
Скачать 1.2 Mb.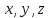 .
. 

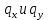 . Она определяется формулами
. Она определяется формулами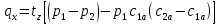
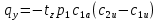
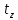 – шаг лопатки по окружности с координатой
– шаг лопатки по окружности с координатой 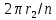 ;
; 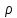 ,
, 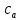 ,
, 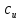
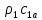 – массовый расход
– массовый расход 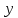 интенсивность
интенсивность 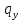 определяется только изменением количества движения. Для компрессора изменения осевых скоростей незначительно, поэтому интенсивность
определяется только изменением количества движения. Для компрессора изменения осевых скоростей незначительно, поэтому интенсивность 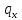 определяется разностью статических давлений и имеет отрицательный знак. Интенсивность
определяется разностью статических давлений и имеет отрицательный знак. Интенсивность 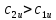 . Для турбины
. Для турбины 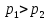 , а
, а 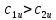 .
.
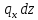 и
и 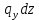 . Элементарные моменты, создаваемые этими силами в сечении с координатой
. Элементарные моменты, создаваемые этими силами в сечении с координатой 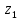 , определяются формулами
, определяются формулами