Кр. Курсовая работа. Департамент образования и науки города москвы государственное бюджетное профессиональное образовательное учреждение города Москвы
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
Колебания лопаток |
| z = |
| 0 |
| 6,9 ∙ 10-3 |
| 0,014 |
| 0,021 |
| 0,028 |
| 0,035 |
| 0,041 |
| 0,048 |
| 0,055 |
| 0,062 |
| 0,069 |
Площадь каждого поперечного сечения рассчитывается по следующей формуле:
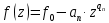 (2.2)
(2.2)Получим следующие площади для каждого поперечного сечения (табл. 2.2).
Табл. 2.2 – Площади поперечных сечений для каждой лопатки
| f1 (z) = | f2 (z) = | f3 (z) = | f4 (z) = |
| 1,31 ∙ 10-4 | 1,31 ∙ 10-4 | 1,31 ∙ 10-4 | 1,31 ∙ 10-4 |
| 9,422 ∙ 10-5 | 1,298 ∙ 10-4 | 1,194 ∙ 10-4 | 1,31 ∙ 10-4 |
| 7,899 ∙ 10-5 | 1,263 ∙ 10-4 | 1,077 ∙ 10-4 | 1,31 ∙ 10-4 |
| 6,73 ∙ 10-5 | 1,205 ∙ 10-4 | 9,611 ∙ 10-5 | 1,31 ∙ 10-4 |
| 5,745 ∙ 10-5 | 1,124 ∙ 10-4 | 8,448 ∙ 10-5 | 1,31 ∙ 10-4 |
| 4,876 ∙ 10-5 | 1,019 ∙ 10-4 | 7,285 ∙ 10-5 | 1,31 ∙ 10-4 |
| 4,091 ∙ 10-5 | 8,913 ∙ 10-5 | 6,122 ∙ 10-5 | 1,31 ∙ 10-4 |
| 3,37 ∙ 10-5 | 7,401 ∙ 10-5 | 4,959 ∙ 10-5 | 1,31 ∙ 10-4 |
| 2,698  10-5 10-5 | 5,657  10-5 10-5 | 3,796  10-5 10-5 | 1,31  10-4 10-4 |
| 2,067  10-5 10-5 | 3,68  10-5 10-5 | 2,633  10-5 10-5 | 1,31  10-4 10-4 |
| 1,47  10-5 10-5 | 1,47  10-5 10-5 | 1,47  10-5 10-5 | 1,31  10-4 10-4 |
Графики распределения площадей представлены на рис. 16 - 17.
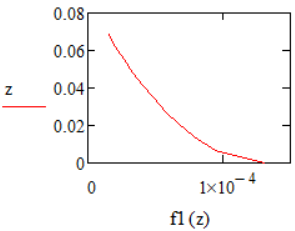 | 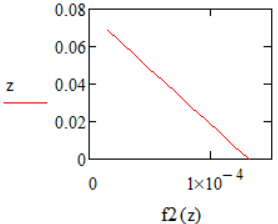 |
| Рис. 16 – График распределения площадей при q = 0,5 | Рис. 17 – График распределения площадей при q = 1 |
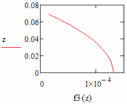 | 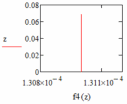 |
| Рис. 18 – График распределения площадей при q = 2 | Рис. 19 – График распределения площадей при a = 0 |
Объем лопатки численно равен площади фигуры под графиком распределения площадей по высоте и связан следующей зависимостью:
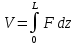 (2.3)
(2.3)Рассчитаем объем лопаток по данной формуле:
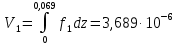 (м3) (объем лопатки с q = 0,5)
(м3) (объем лопатки с q = 0,5)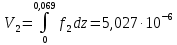 (м3) (объем лопатки с q = 1)
(м3) (объем лопатки с q = 1)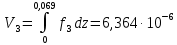 (м3) (объем лопатки с q = 2)
(м3) (объем лопатки с q = 2)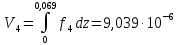 (м3) (объем лопатки с a = 0)
(м3) (объем лопатки с a = 0)Подсчитаем массы лопаток по следующей формуле:
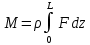 (2.4)
(2.4)Получим следующие массы:
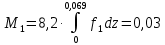 (кг) (масса лопатки с q = 0,5)
(кг) (масса лопатки с q = 0,5)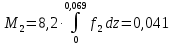 (кг) (масса лопатки с q = 1)
(кг) (масса лопатки с q = 1)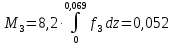 (кг) (масса лопатки с q = 2)
(кг) (масса лопатки с q = 2)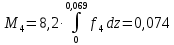 (кг) (масса лопатки с a = 0)
(кг) (масса лопатки с a = 0)Массы каждого участка лопатки представлены в табл. 2.3:
Табл. 2.3 – Массы каждого участка лопатки
| M1 = | M2 = | M3 = | M4 = |
| 0,03 | 0,052 | 0.041 | 0,074 |
| 0,024 | 0,045 | 0,034 | 0,067 |
| 0,019 | 0,038 | 0,028 | 0,059 |
| 0,015 | 0,031 | 0,022 | 0,052 |
| 0,012 | 0,024 | 0,017 | 0,044 |
| 8,701 ∙ 10-3 | 0,018 | 0,012 | 0,037 |
| 6,168 ∙ 10-3 | 0,012 | 8,591∙ 10-3 | 0,03 |
| 4,06 ∙ 10-3 | 7,825∙ 10-3 | 5,456∙ 10-3 | 0,022 |
| 2,345 ∙ 10-3 | 4,12 ∙ 10-3 | 2,98∙ 10-3 | 0,015 |
| 9,991 ∙ 10-4 | 1,468 ∙ 10-3 | 1,161∙ 10-3 | 7,412 ∙ 10-3 |
| 0 | 0 | 0 | 0 |
Формула для определения центробежной силы в каждом участке:
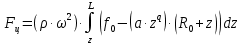 (2.5)
(2.5)Центробежная сила в каждом участке показана в табл. 2.4.
Таблица 2.4 – Центробежная сила в каждом участке лопатки
| Fц1 = | Fц2 = | Fц3 = | Fц4 = |
| 9,302 ∙ 103 | 1,033 ∙ 104 | 1,137 ∙ 104 | 1,352 ∙ 104 |
| 8,074 ∙ 103 | 9,007 ∙ 103 | 1,002 ∙ 104 | 1,217 ∙ 104 |
| 6,951 ∙ 103 | 7,744 ∙ 103 | 8,683 ∙ 103 | 1,082 ∙ 104 |
| 5,901 ∙ 103 | 6,543 ∙ 103 | 7,368 ∙ 103 | 9,466 ∙ 103 |
| 4,91 ∙ 103 | 5,405 ∙ 103 | 6,092 ∙ 103 | 8,114 ∙ 103 |
| 3,974 ∙ 103 | 4.332 ∙ 103 | 4,866 ∙ 103 | 6,762 ∙ 103 |
| 3,088 ∙ 103 | 3,326 ∙ 103 | 3,704 ∙ 103 | 5,409 ∙ 103 |
| 2,25 ∙ 103 | 2,388 ∙ 103 | 2,622 ∙ 103 | 4,057 ∙ 103 |
| 1,456 ∙ 103 | 1,52 ∙ 103 | 1,633 ∙ 103 | 2,705 ∙ 103 |
| 706,96 | 723,194 | 754,034 | 1,352 ∙ 103 |
| 0 | 0 | 0 | 0 |
На рисунках 20 – 23 показаны графики центробежной силы в каждом участке лопатки.
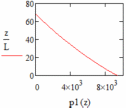 | 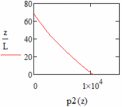 |
| Рис. 20 – График центробежной силы в каждом участке лопатки при q = 0,5 | Рис. 21 – График центробежной силы в каждом участке лопатки при q = 1 |
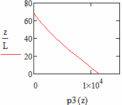 | 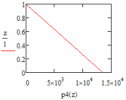 |
| Рис. 22 – График центробежной силы в каждом участке лопатки при q = 2 | Рис. 23 – График центробежной силы в каждом участке лопатки при a = 0 |
Формула напряжения в сечениях лопатки:
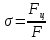 (2.6)
(2.6)Напряжения в сечениях лопатки показаны в табл. 2.5.
Таблица 2.5 – Напряжения в сечениях лопатки
| σ1 = | σ2 = | σ3 = | σ4 = |
| 7,101 ∙ 107 | 7,885 ∙ 107 | 8,68 ∙ 107 | 1,032 ∙ 108 |
| 8,569 ∙ 107 | 7,545 ∙ 107 | 7,718 ∙ 107 | 9,291 ∙ 107 |
| 8,8 ∙ 107 | 7,188 ∙ 107 | 6,872 ∙ 107 | 8,259 ∙ 107 |
| 8,768 ∙ 107 | 6,808 ∙ 107 | 6,113 ∙ 107 | 7,226 ∙ 107 |
| 8,548 ∙ 107 | 6,398 ∙ 107 | 5,42 ∙ 107 | 6,194 ∙ 107 |
| 8,15 ∙ 107 | 5,946 ∙ 107 | 4,774 ∙ 107 | 5,162 ∙ 107 |
| 7,548 ∙ 107 | 5,432 ∙ 107 | 4,156 ∙ 107 | 4,129 ∙ 107 |
| 6,677 ∙ 107 | 4,815 ∙ 107 | 3,542 ∙ 107 | 3,097 ∙ 107 |
| 5,399 ∙ 107 | 4,003 ∙ 107 | 2,887 ∙ 107 | 2,065 ∙ 107 |
| 3,421 ∙ 107 | 2,747 ∙ 107 | 2,049 ∙ 107 | 1,032 ∙ 107 |
| 0 | 0 | 0 | 0 |
На рисунках 24 – 27 показаны графики напряжения в сечениях лопатки.
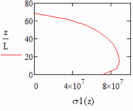 | 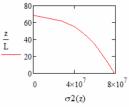 |
| Рис. 24 – График напряжения в сечениях лопатки при q = 0,5 | Рис. 25 – График напряжения в сечениях лопатки при q = 1 |
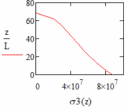 | 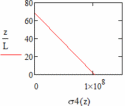 |
| Рис. 26 – График напряжения в сечениях лопатки при q = 2 | Рис. 27 – График напряжения в сечениях лопатки при a = 0 |
Как видно из графиков распределения напряжений самый оптимальный вариант — это лопатка с законом профилирования q = 0,5 (рис. 24) у этой лопатки в связи с небольшой массой получаются самые низкие напряжения в корневом сечении.
При этом максимум напряжений приходится не на корневое сечение, которое является самым опасным. Далее будет произведен расчет от действия газодинамической силы этой лопатки.

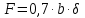 (м2)
(м2)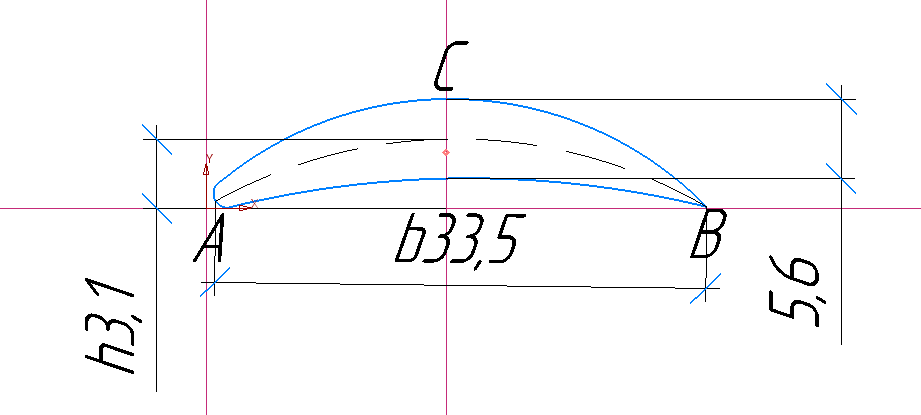
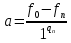 (2.1)
(2.1)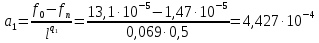 ;
;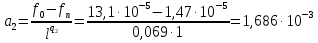 ;
;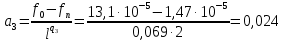 ;
;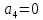 (для лопатки постоянного сечения)
(для лопатки постоянного сечения)