деревья и взвешенные графы. Деревья и взвешенные графы
 Скачать 276.07 Kb. Скачать 276.07 Kb.
|
|
Государственное бюджетное профессиональное образовательное учреждение Ленинградской области «Подпорожский политехнический техникум» Тема реферата: «Деревья и взвешенные графы» Гайнова Дарья Андреевна 230 группа Руководитель: Шмакова Елена Евгеньевна Город Подпорожье 2023г Содержание 1.1 Дерево это ……………………………………………………………3 1.2 Примеры задач с деревьями…………………………………………………………………4-6 2.1 Взвешенные графы………………………………………………….7 1.1 Дерево это Дерево — это связный граф без циклов. Оно состоит из вершин и ребер, каждое из которых соединяет две вершины. Каждая вершина имеет не более одного предка, кроме одной, которая является корнем дерева. Деревья имеют множество приложений в информатике и других областях науки. Например, они используются в алгоритмах поиска и сортировки данных, в криптографии, в теории кодирования и многих других областях. Так могут быть использованы для решения многих задач, таких как поиск в глубину и ширину, алгоритм Прима и Крускала, и алгоритм Дейкстры. Алгоритмы на основе деревьев используются в многих областях, таких как маршрутизация пакетов в компьютерных сетях и поиск кратчайшего пути в графах. 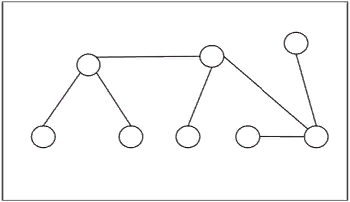 3 1.2 Примеры задач с деревьями Задачи № 1. Докажите, что граф, в котором любые две вершины соединены ровно одним простым путем, является деревом. Решение: Очевидно, что данный граф связен. Предположим теперь, что в нем есть цикл. Тогда любые две вершины этого цикла соединены по крайней мере двумя простыми путями. Получили противоречие, значит, наше предположение неверно. 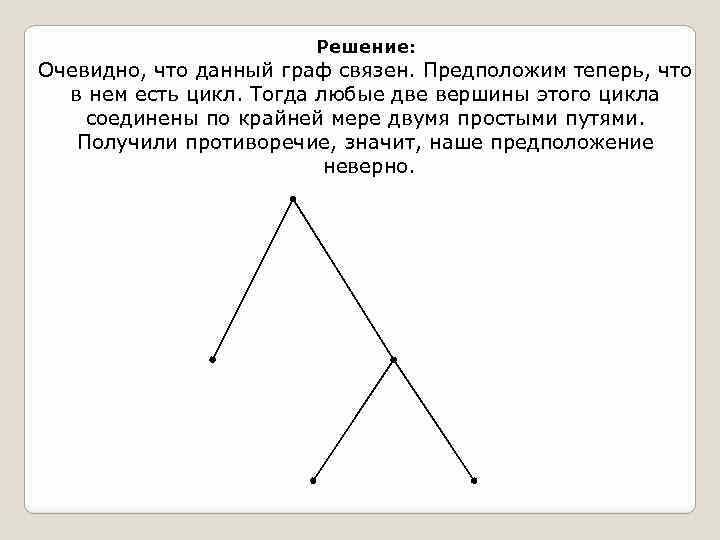 Задание № 2. Докажите, что при удалении любого ребра из дерева оно превращается в несвязный граф. Решение: Предположим, что концы удаленного ребра в новом графе соединены простым путем. Тогда этот путь вместе с удаленным ребром образует в исходном графе цикл. 4 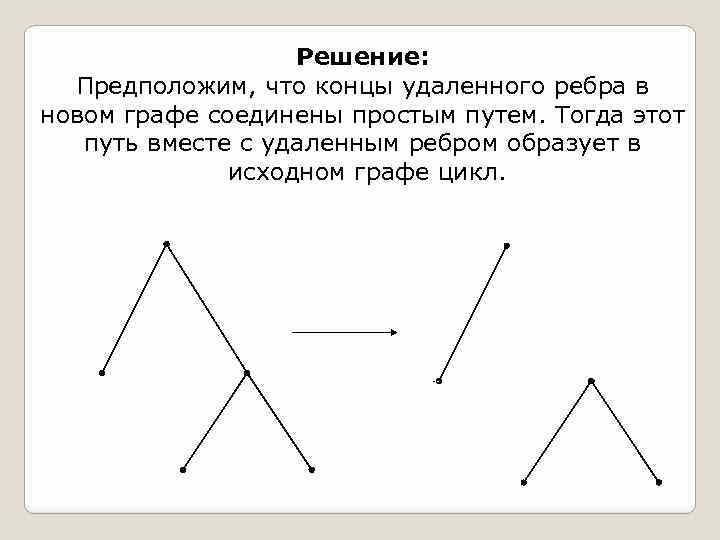 Задание №3 Докажите, что в дереве любые две вершины соединены ровно одним простым путем. Решение: Предположим, противное и рассмотрим те две вершины, которые соединены двумя разными простыми путями. На первый взгляд кажется, что пройдя от одной вершины к другой по первому пути, и вернувшись по второму, мы получим цикл. К сожалению, этой не совсем так. Дело в том, что первый и второй пути могут иметь общие вершины (кроме начала и конца), а по определению цикла вершины в нем не должны повторяться. Для того, чтобы выделить настоящий цикл из уже полученного нужно сделать 1) выбрать первую точку, в которой пути расходятся 2) за выбранной точкой на пути 1 найти первую точку, принадлежащую также и пути 2 5 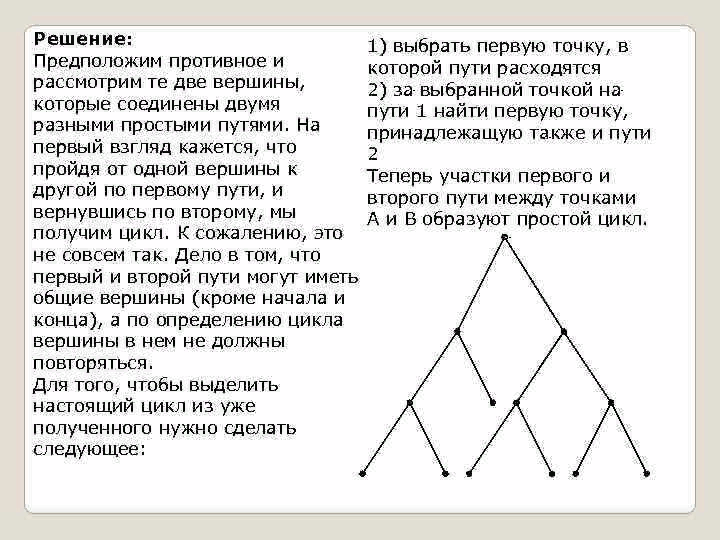 6 2.1 Взвешенные графы Взвешенный граф — это граф, в котором каждое ребро обозначается числом. Это число — его вес: 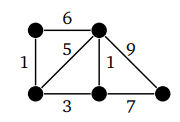 Вес — это стоимость использования данного ребра. Например, приведенный выше граф может представлять дорожную сеть, где вершины — это города, ребра — дороги между ними, а вес — стоимость строительства этих дорог. Существует несколько алгоритмов, чтобы найти минимальные прямые деревья. В этом уроке мы рассмотрим алгоритм Крускала. Алгоритм Крускала строит охватывающее дерево графа по одному ребру за раз. На каждом шаге алгоритма мы берем ребро с таким весом, чтобы добавление этого ребра в строящееся дерево не создавало цикла. 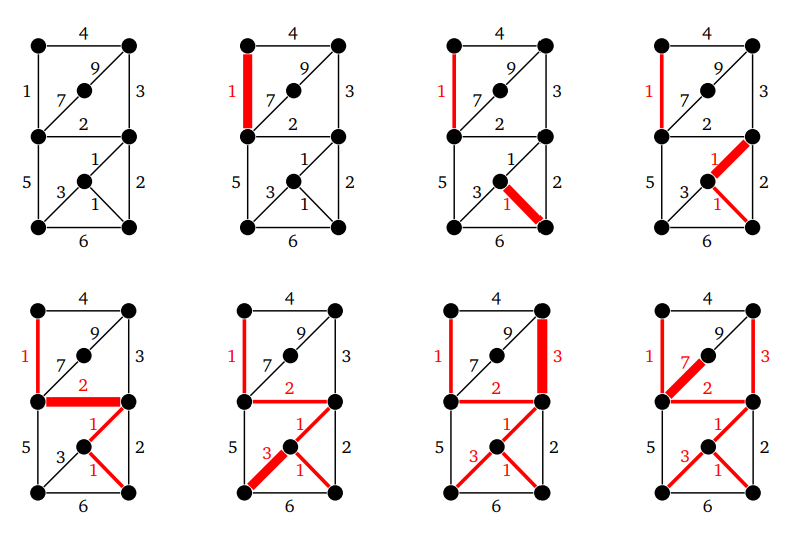 Так это выглядит (грани выделены в порядке их добавления) 7 |
