19 Неделя Лебедев Лев_. Дериватография. Применение дериватографии
 Скачать 165.25 Kb. Скачать 165.25 Kb.
|
|
Обработка дериватограмм Обработка полученных дериватограмм заключается в качественном и количественном анализе кривых Т, ТГ, ДТА и ДТГ. К изучению кинетики процессов термодеструкции по данным термогравиметрического анализа существует ряд подходов. Наиболее разработаны они для тех случаев, когда процесс проходит в одну стадию или стадии далеко разнесены по температурным интервалам и потому легко поддаются разделению на отдельные брутто-процессы. Как правило, предполагают протекание процесса по уравнению скорости реакции порядка х, подчиняющейся зависимости Аррениуса: 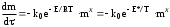 , ,где m — масса нелетучего вещества пробы в момент времени , Е — энергия активации, k0 — предэкспоненциальный множитель, R — универсальная газовая постоянная, Т — абсолютная температура, х — порядок реакции. Следует заметить, что в данном случае речь должна идти не о кинетических константах вполне определенных реакций индивидуальных веществ, а о некоторых параметрах суммарных процессов термического разложения, описывающих зависимость изменения общей массы образца при повышении его температуры с определенной скоростью. По этой причине часто невозможно использовать величины k0, Е и х, определенные в одних условиях термодеструкции, для описания термического разложения того же вещества, в других условиях, например, с другой скоростью подъема температуры. Часто для определения кинетических параметров реакции используют одну точку кривой ТГ с максимальной скоростью деструкции, и полученные результаты переносят на всю кривую в целом, что не всегда обоснованно. Тем более такой способ неприемлем при недостаточной определенности системы, включающей три неизвестных параметра. Например, сначала по степени превращения массы исходного вещества в точке перегиба оценивают порядок реакции деструкции, а затем, зная порядок, степень превращения и температуру в этой точке, определяют энергию активации и предэкспоненциальный множитель изучаемого процесса. Очевидно, что при таком подходе при расчете каждого следующего параметра ошибка его определения нарастает очень быстро. Правда, определенность системы можно повысить, приняв х=1, что для процессов деструкции часто является оправданным. Выбор первого порядка выгоден также тем, что размерность k0 включает тогда только время, и безразлично, в каких единицах измеряется количество вещества. Более перспективны методы, использующие для определения кинетических параметров процесса весь участок кривой ТГ, относящийся к одной брутто-стадии. Этот путь позволяет заметно повысить надежность их определения, хотя и требует большой вычислительной работы с применением ЭВМ. Рассмотрим один из таких методов. Пусть исходное вещество А последовательно разлагается, образуя промежуточный твердый продукт В и летучий продукт Р1. Затем В переходит в следующий промежуточный продукт С и выделяет летучий продукт Р2 и т.д.: 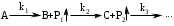 Скорость выделения летучих веществ на каждой стадии, как правило, можно описать уравнением реакции первого порядка с последующим определением констант скорости стадий. Процесс термической деструкции в целом будет отвечать схеме последовательных реакций первого порядка. Допустим, что за скоростью процесса следят по общему накоплению летучих веществ, т.е. измеряют их массу за определенный промежуток времени, а число стадий деструкции равно двум (рис. 4). Масса выделившихся летучих веществ при этом равна потере массы твердого образца. 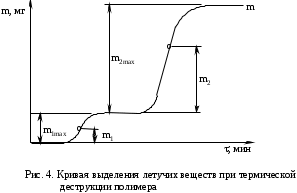 Как видно из рис. 4, кинетическая кривая выделения летучих веществ состоит из двух стадий, и каждая из стадий представлена S-образной линией. Такая форма объясняется тем, что сначала скорость реакции растет за счет увеличения константы скорости по уравнению Аррениуса, а затем скорость деструкции падает в связи с разложением реагента. Масса летучих веществ, выделяющихся на каждой стадии, различна, а число молей, участвующих в реакции, неизвестно. В связи с этим будем условно считать, что на каждой стадии разлагается одно и то же число молей реагента, равное числу молей исходного вещества nA,0. Максимальное число молей летучих продуктов, которое может выделиться на каждой стадии, также будет равно nA,0: nA,0 = nР1max = nР2max. Скорость выделения летучих веществ на некоторой стадии разложения будет определяться числом молей твердого исходного или промежуточного вещества. Тогда система уравнений, описывающих двухстадийный процесс термодеструкции твердой фазы, может быть представлена в виде: 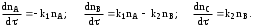 Скорости выделения летучих веществ: 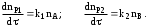 Из соотношений материального баланса: nA,0 = nA+nВ+nС; с другой стороны, nA,0 = nA+nР1, nС = nP2. Тогда nВ = nA,0—nА—nС или nВ = nР1—nР2, и система уравнений будет иметь вид: 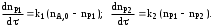 Текущая масса выделившихся на данной стадии летучих веществ mi пропорциональна текущему числу молей nPi (где i — номер стадии кинетической кривой выделения летучих веществ): 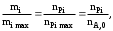 откуда следует, что 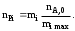 Подставив это выражение в систему уравнений, описывающих скорости выделения летучих веществ, получим: 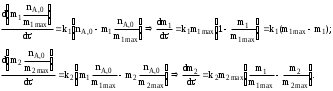 (1) (1)В нашем случае стадии разложения далеко разнесены во времени, поэтому к началу второй стадии выделение летучих веществ по первому уравнению уже прекратилось и m1=m1max. Тогда полученная система уравнений упрощается: 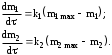 (2) (2)При этом первое уравнение остается без изменений, а второе получено за счет преобразования 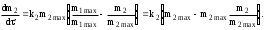 Общая потеря массы исходного вещества и скорость выделения летучих веществ: 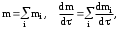 в частности, для нашего случая двух стадий деструкции: 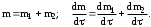 Изучаемый процесс протекает в неизотермических условиях, поэтому константы скорости k1 и k2 изменяются в ходе эксперимента в соответствии с уравнением Аррениуса. Как правило, процесс проводят таким образом, что температура образца линейно зависит от времени реакции, не меняясь по объему образца: Т = Т0+, где Т0 — начальная температура, К; — скорость подъема температуры, К/мин. Тогда аррениусовская зависимость констант на i-й стадии запишется как 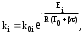 а уравнение скорости i-й стадии реакции первого порядка 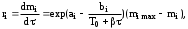 где ai=lnk0i; bi=Ei/R. Величины скорости изменения массы образца определяются экспериментально как тангенс угла наклона касательной к кривой в заданных точках. Подбор параметров ai=lnk0i и bi=Ei/R осуществляется путем линеаризации уравнения скорости соответствующей стадии: 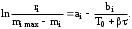 Это уравнение прямой линии в координатах 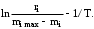 ai — отсекаемый отрезок ординаты, bi — тангенс угла наклона. В том случае, если зависимость оказывается нелинейной, следует уточнить величины mi max. Величины аi и bi должны быть постоянными при различных скоростях подъема температур в относительно небольшом интервале ( = 3÷15 К/мин), в противном случае предложенную кинетическую модель следует считать неадекватной эксперименту. Пример. Получена кривая термической деструкции твердого органического вещества, обнаруживающая две макростадии процесса. Из нее получены величины массы выделившихся летучих веществ, приведенные в табл. 1. Скорость подъема температуры составляет 5оС/мин, начальная температура образца 25оС. Максимальная потеря массы 500 мг. Определить активационные параметры процесса. Решение. Построим кривую массы выделившихся летучих веществ. Установим величины mi max по горизонтальным участкам кривой (m1max=150 мг, m2max=500—150=350 мг). Проведем касательные к кривой в точках, в которых скорость процесса заметно отличается от нуля, рассчитаем температуру по формуле t=25+5 и внесем данные в табл. 1. Таблица 1 Результаты обработки кинетической кривой термодеструкции органического вещества
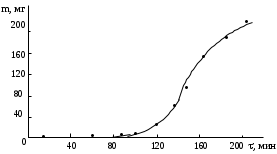
Построим зависимости -ln[ri/(mimax-mi)] от 103/Т (рис. 5). 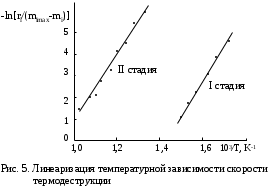 Обработка полученных прямых линий с помощью МНК дала следующие результаты: I стадия lnk0 = 22,41,3; E/R = (15600800) К II стадия lnk0 = 14,41,0; E/R = (15100900) К. Далее кинетические параметры следует уточнить с помощью численного интегрирования системы дифференциальных уравнений (1) или (2) и последующей минимизации остаточной суммы квадратов отклонений экспериментальных и расчетных значений потери массы Z2 при изменении параметров «a» и «b» в своих доверительных интервалах. Если форма кривой ТГ не позволяет достаточно точно установить величины mi max, то они также могут быть уточнены после интегрирования. Такой подход к обработке кривой ТГ может быть применен и для реакций термической деструкции с порядком, отличным от первого, а также в условиях неравномерного подъема температуры. В этом случае уравнение скорости реакции будет иметь вид: 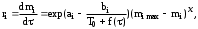 где f() — вид зависимости температуры образца от времени; х — порядок реакции. Рассмотрим ряд примеров обработки кривых потери массы ряда углеродсодержащих веществ. Термическая деструкция нефтяного пека Кривая ТГ нефтяного пека обнаруживает одну брутто-стадию термического разложения (рис. 6).
Величина m1max составляет 220 мг, скорость подъема температуры — 2,5 К/мин. Обработка кинетической кривой дифференциальным методом дала следующие значения активационных параметров а1=7,970,90, b1=7900600 K. Далее каждый доверительный интервал этих параметров разбили на равные отрезки (табл. 2) и произвели численное интегрирование дифференциального уравнения 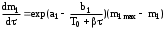 в узлах получившейся сетки. Величины Z2 (мг2), полученные в каждом расчете, приведены в табл. 2. Таблица 2 Остаточные суммы квадратов потери массы m1 при варьировании величин а и b в их доверительных интервалах
Как видно из табл. 2, минимум Z2 был получен на границе исследованной области. Проведение проверочного расчета при дальнейшем увеличении параметров показало возрастание этой суммы, поэтому в качестве значений lnk0 и E/R были приняты 8,87 и 8500 К соответственно. Расчетные значения нанесены на экспериментальную кривую (рис. 6). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||