|
|
математика краткая теория 2 курс. Дифференциальное исчисление функций нескольких переменных
Тема: «Дифференциальное исчисление
функций нескольких переменных»
Краткие теоретические сведения.
Частные производные первого порядка. Дана функция 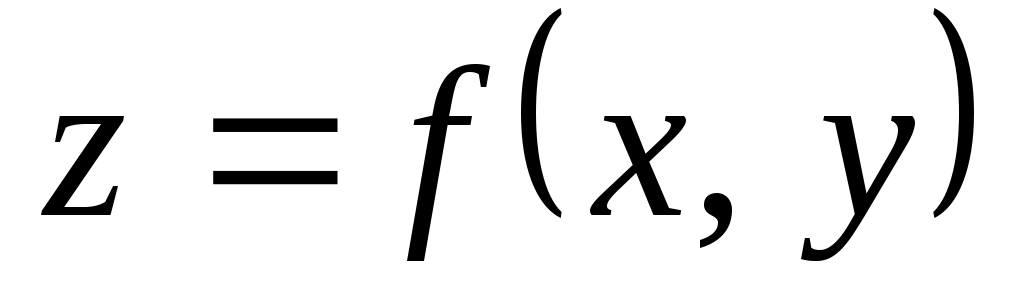 . .
При нахождении частной производной по одному аргументу второй аргумент считается постоянной величиной
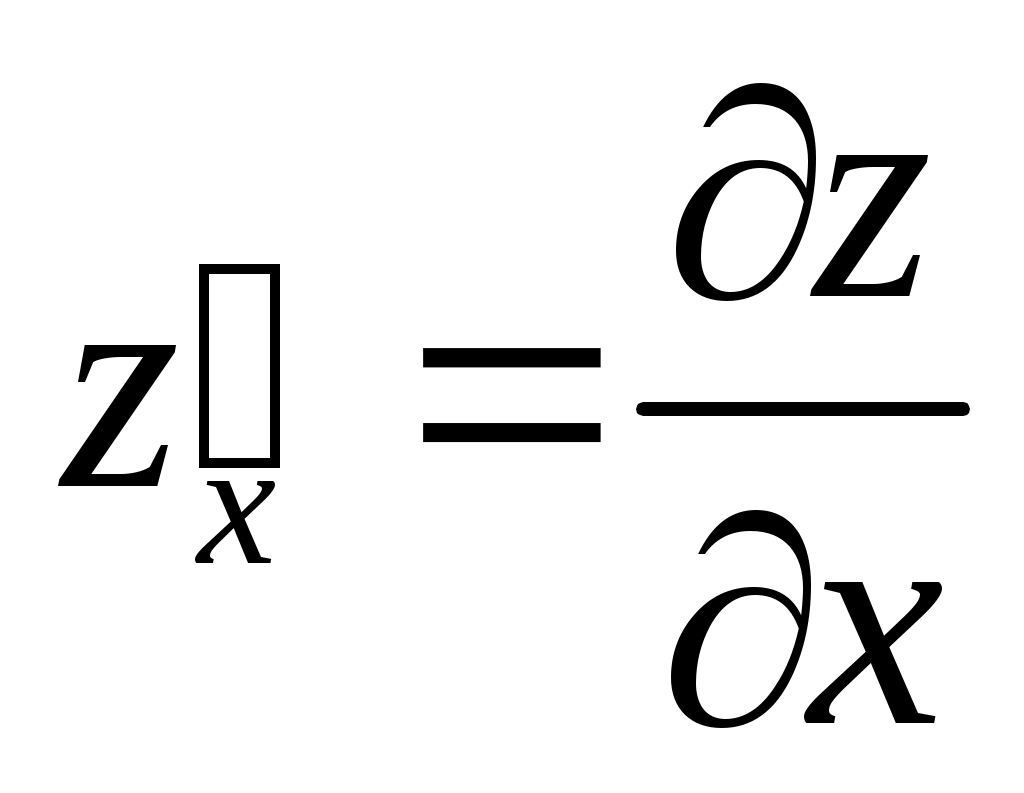 (аргумент у – постоянная величина); (аргумент у – постоянная величина); 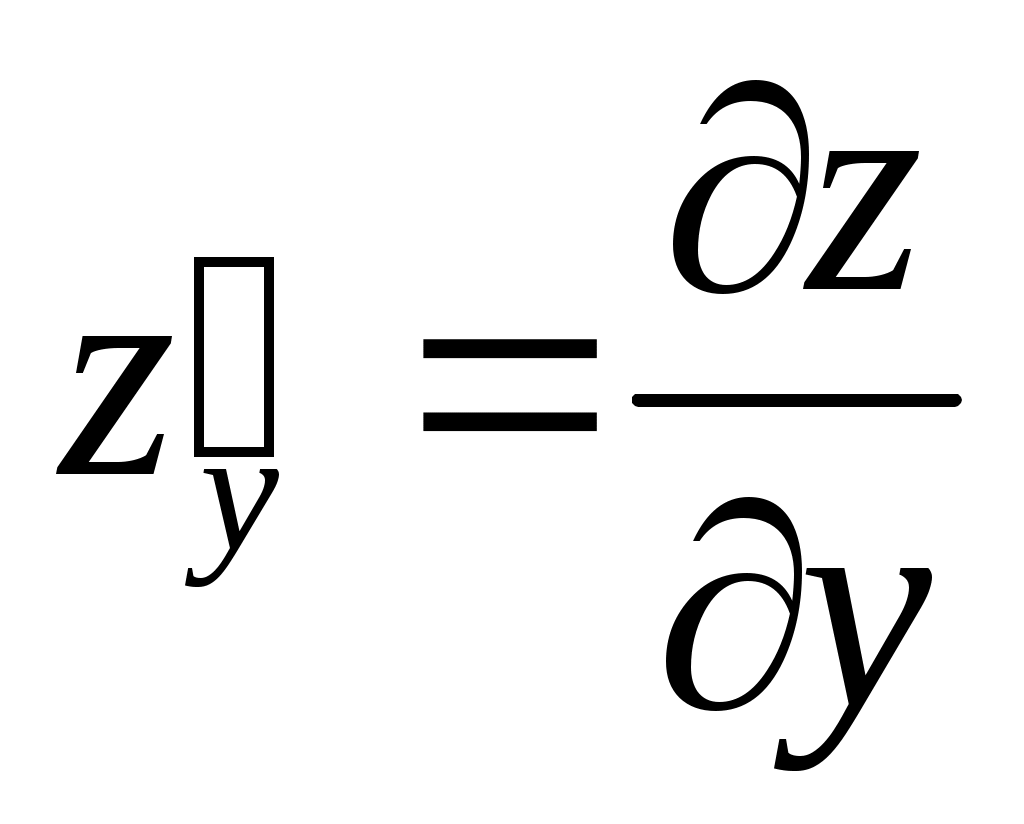 (аргумент х – постоянная величина) (аргумент х – постоянная величина)
Например: 1) 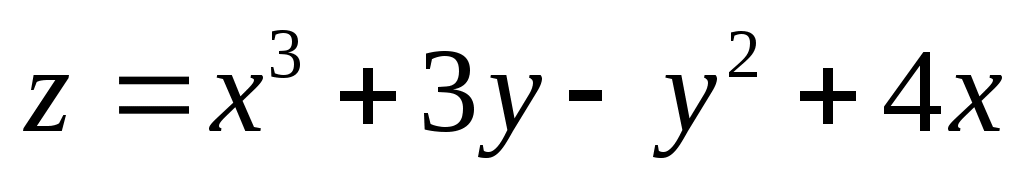 , , 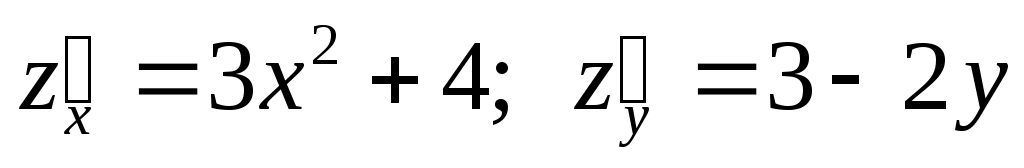 ; ;
2) 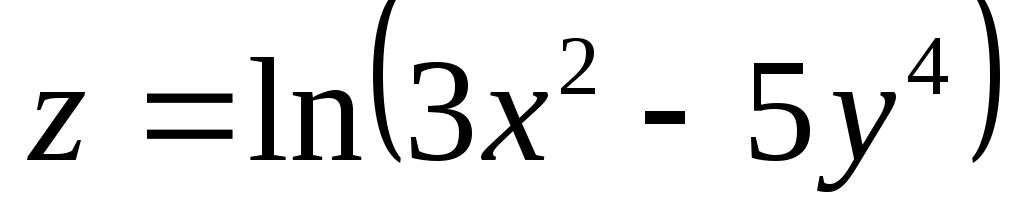 , , 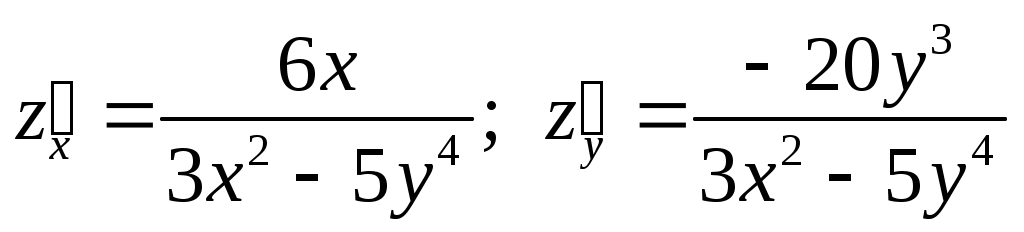 (используем формулу (используем формулу 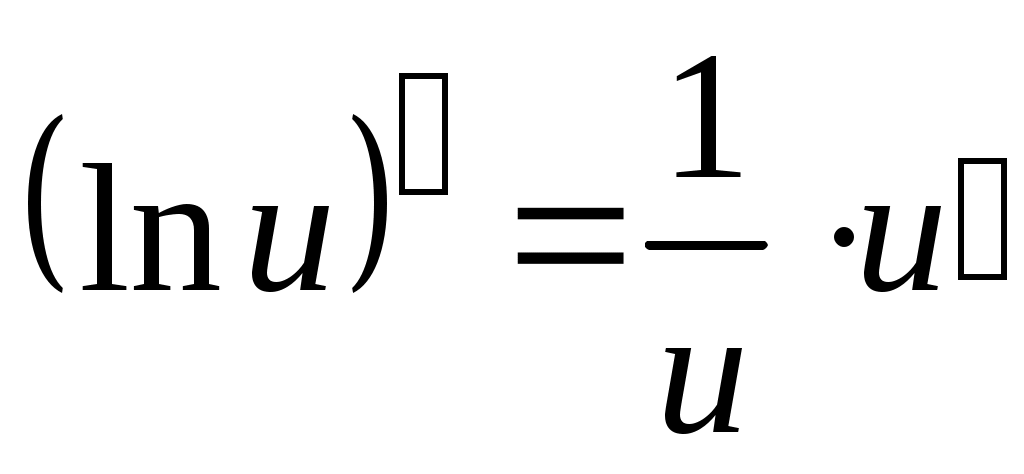 ). ).
Частные производные второго порядка находятся как производные от производных первого порядка.
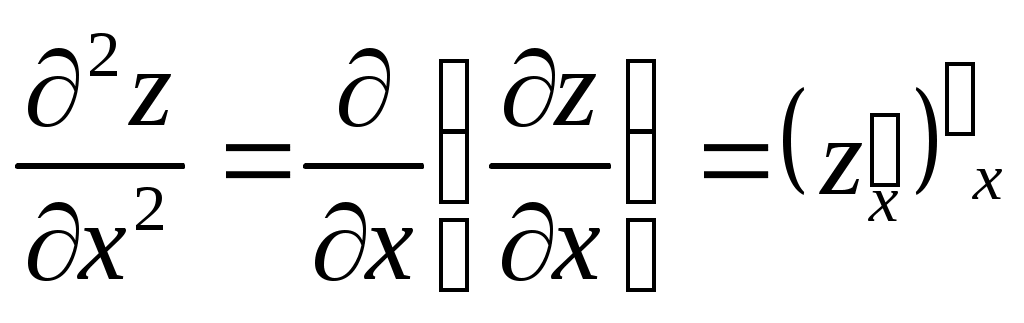 ; ; 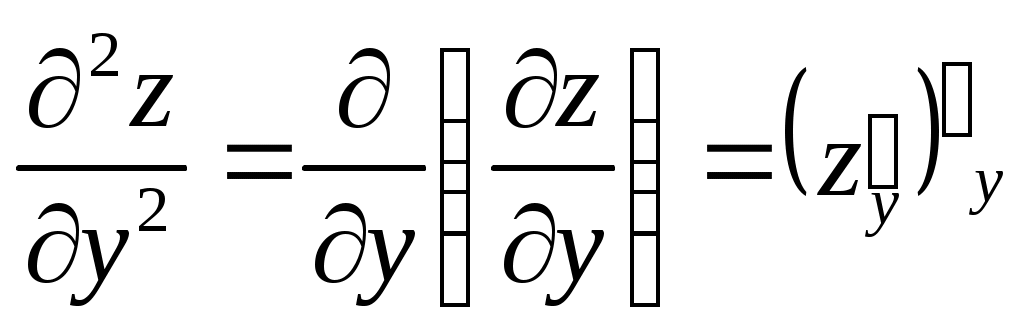 ; ; 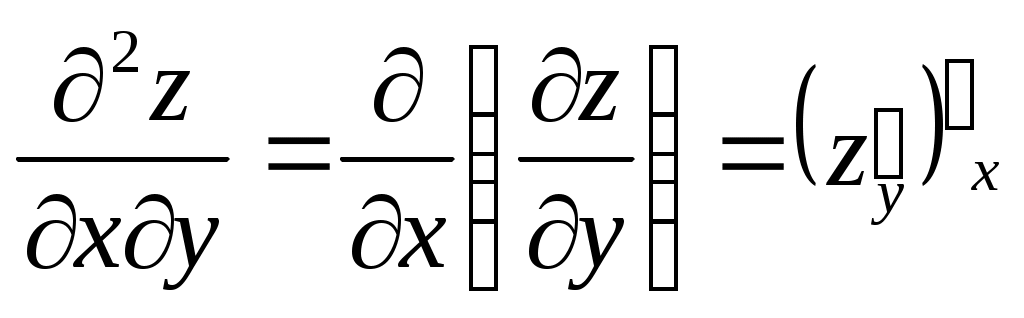 ; ; 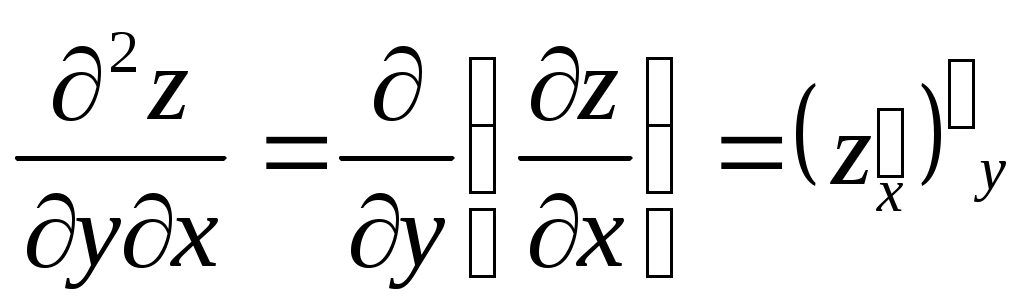 . .
Пример, 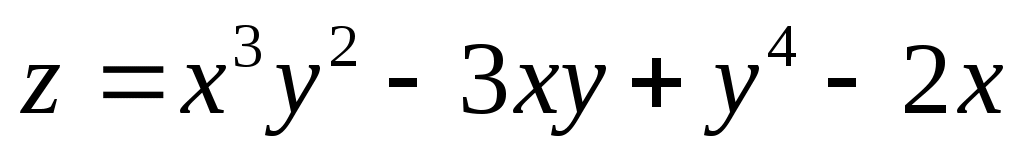 , ,
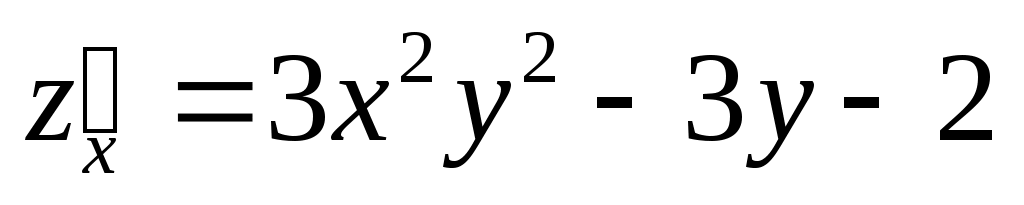 ; ; 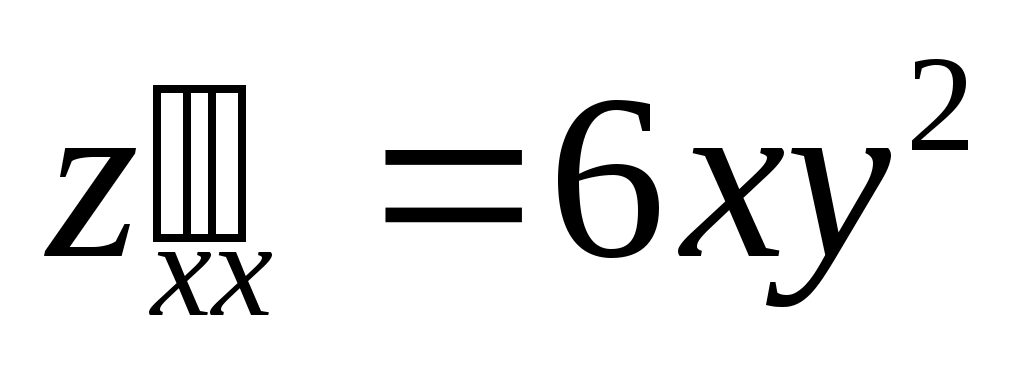 ; ; 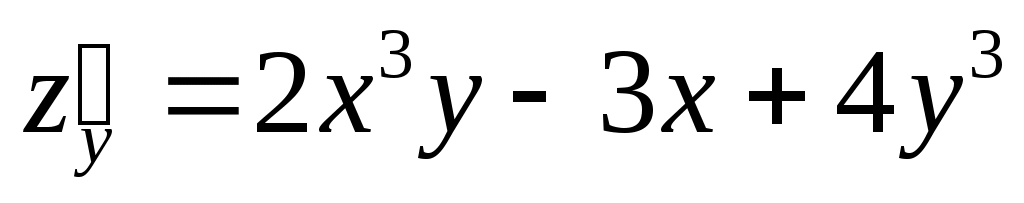 ; ; 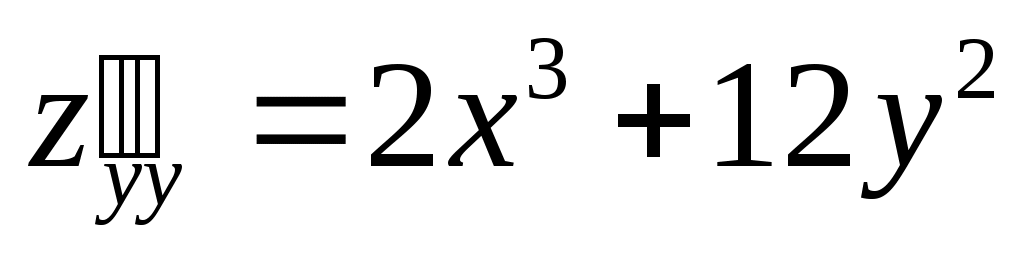
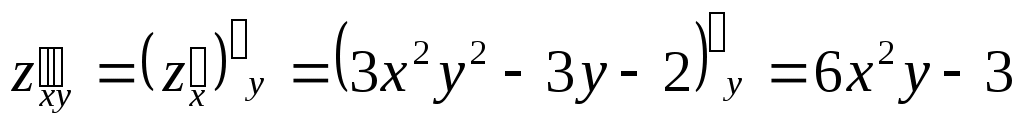 ; ; 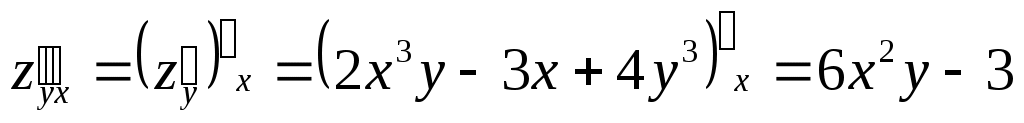 . . 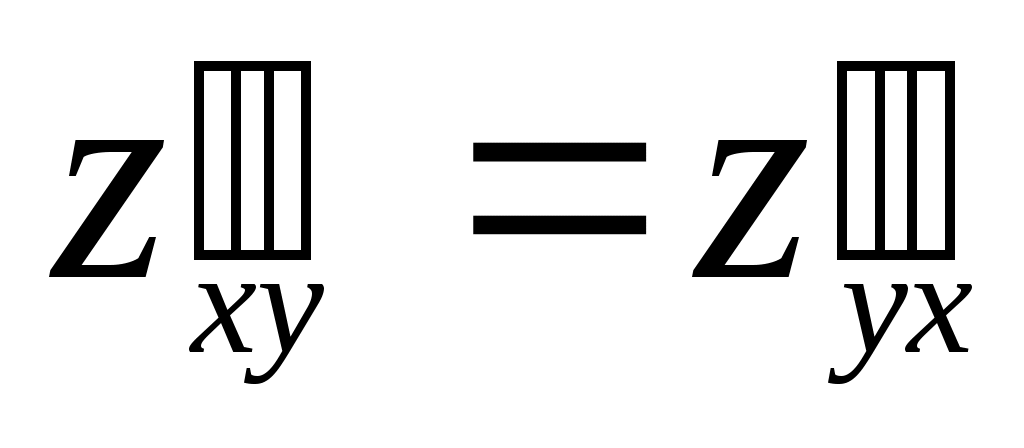 . .
Градиент скалярного поля 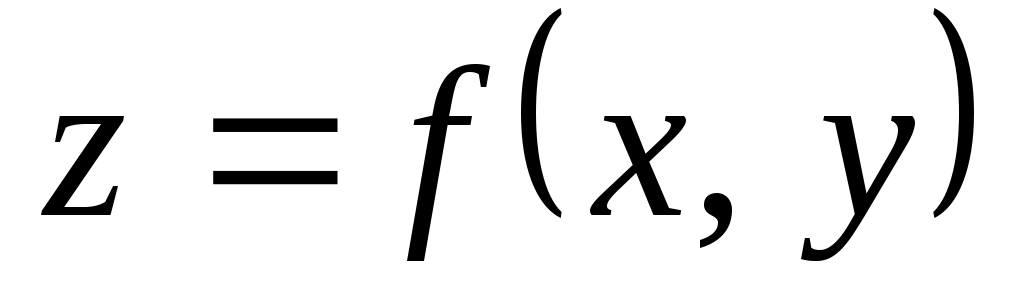 – вектор с координатами – вектор с координатами 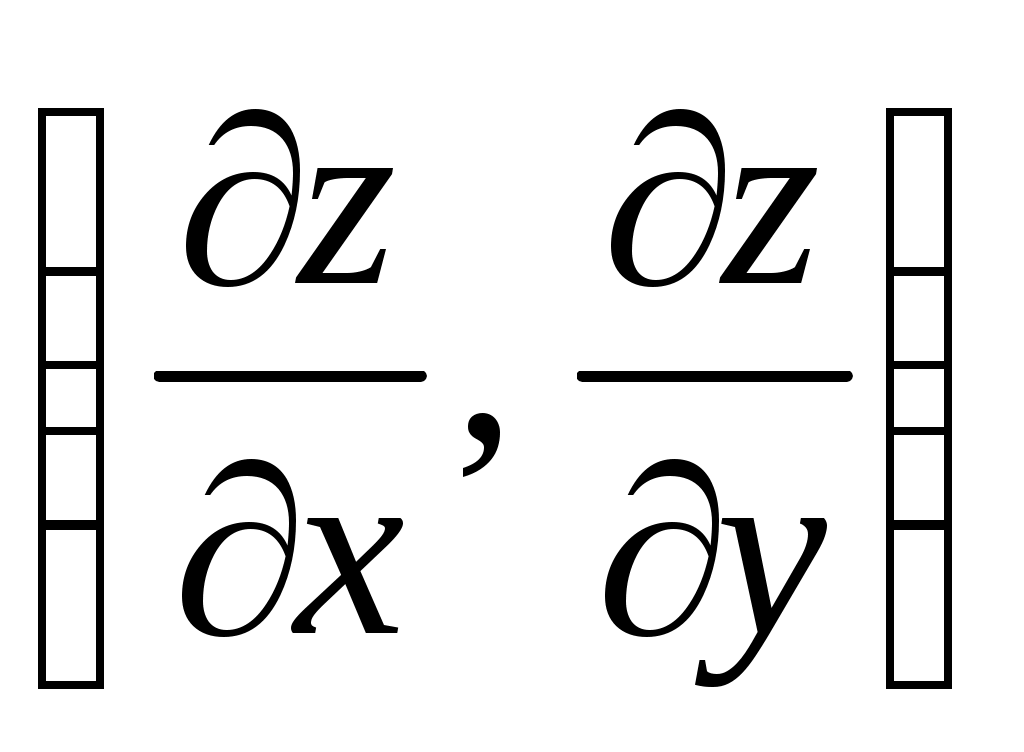 . Этот вектор направлен по нормали к линии уровня . Этот вектор направлен по нормали к линии уровня 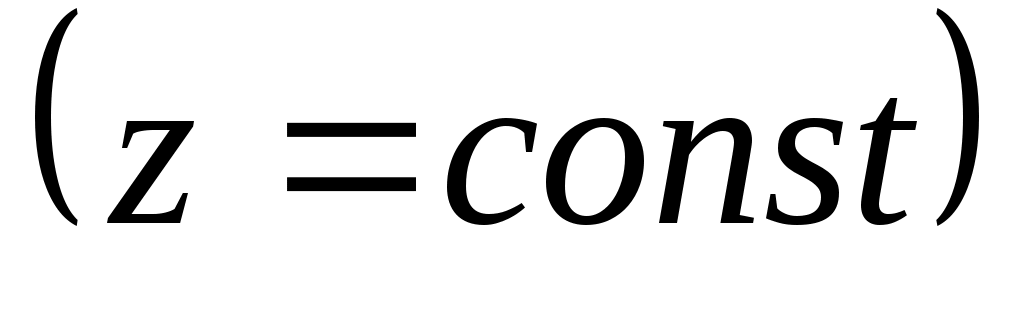 и характеризует направление наибольшего возрастания функции z. и характеризует направление наибольшего возрастания функции z.
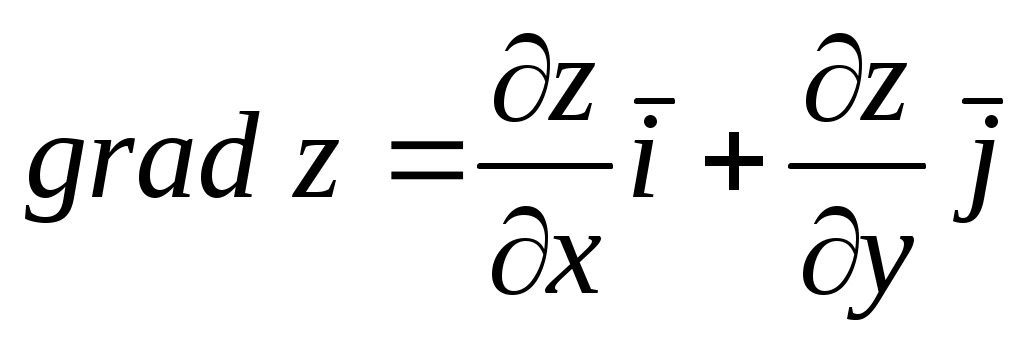 . .
Пример 2: Дана функция 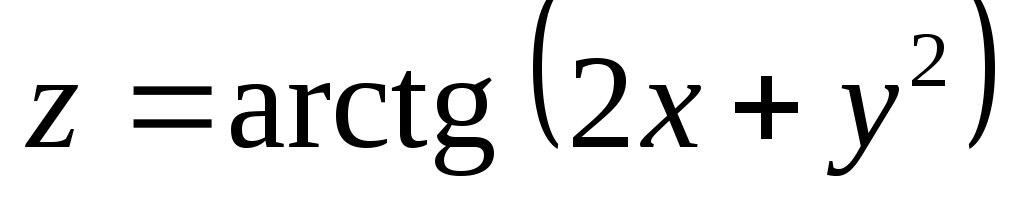 . Найти . Найти 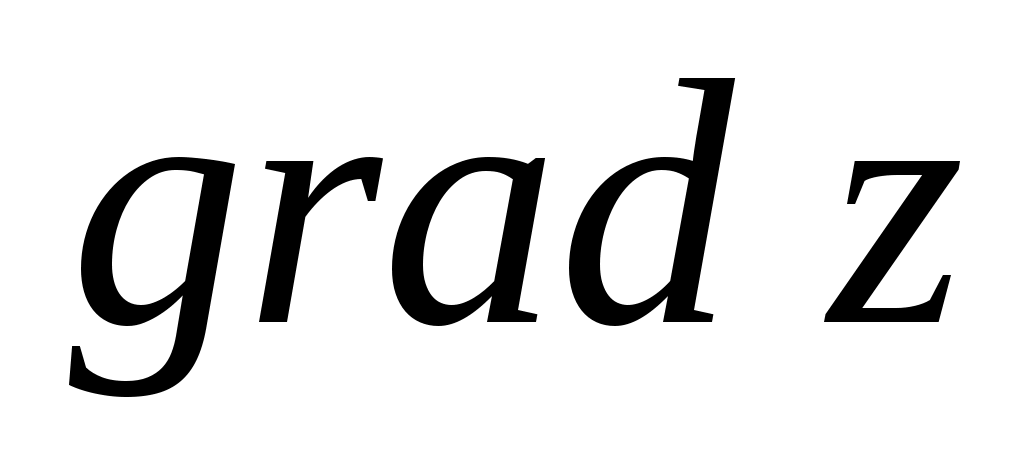 в точке в точке 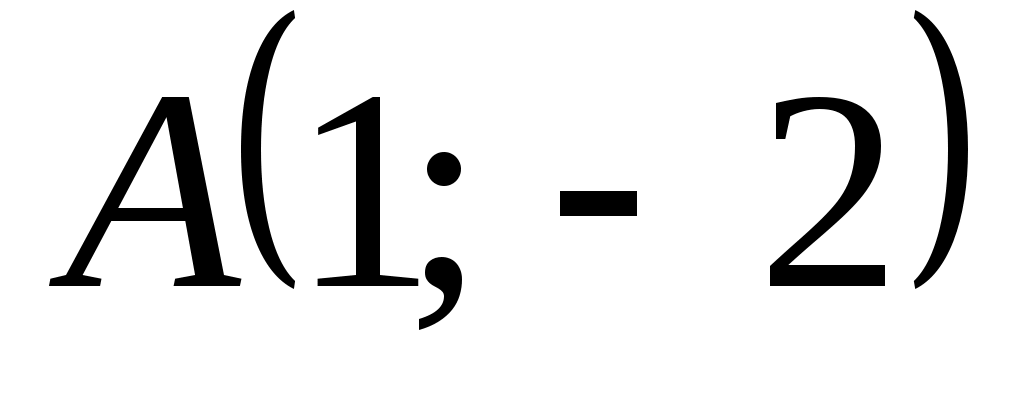 . .
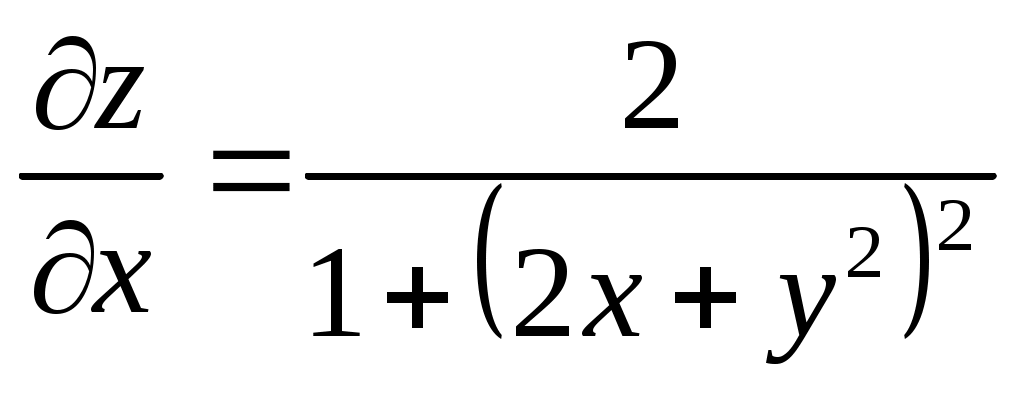 ; ; 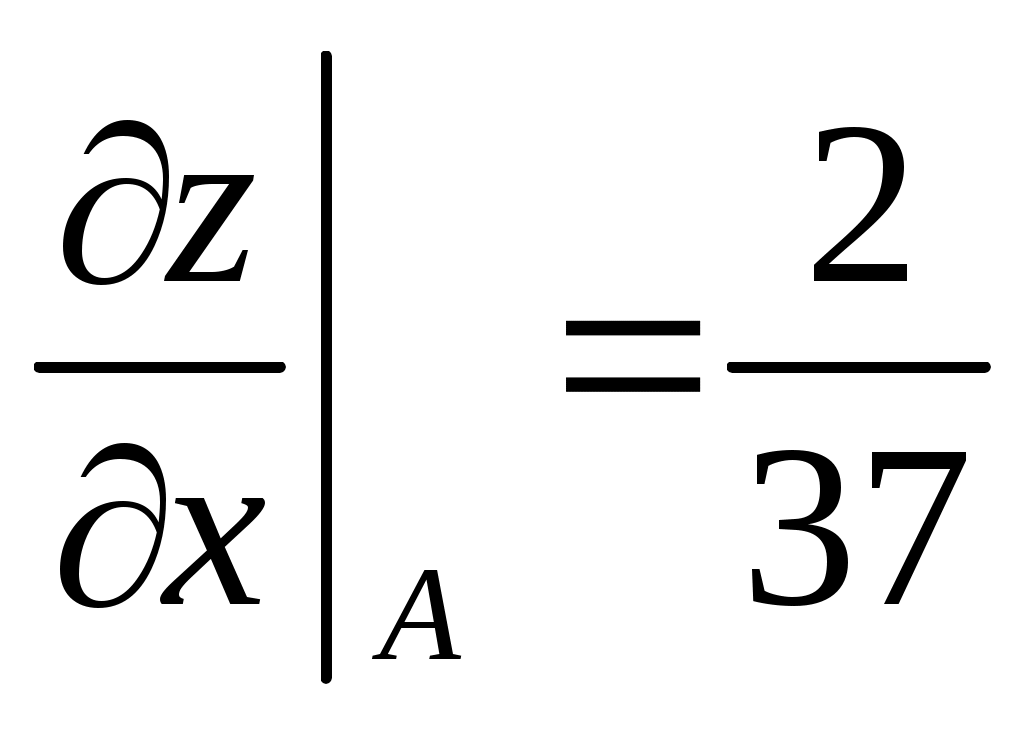 ; ; 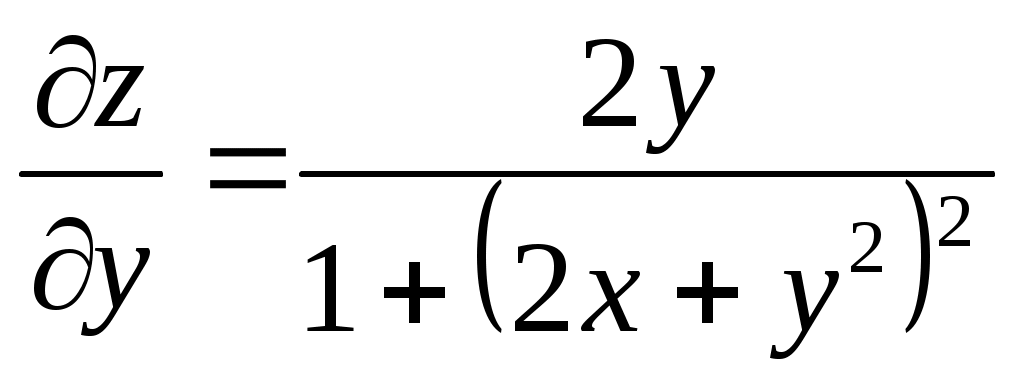 ; ; 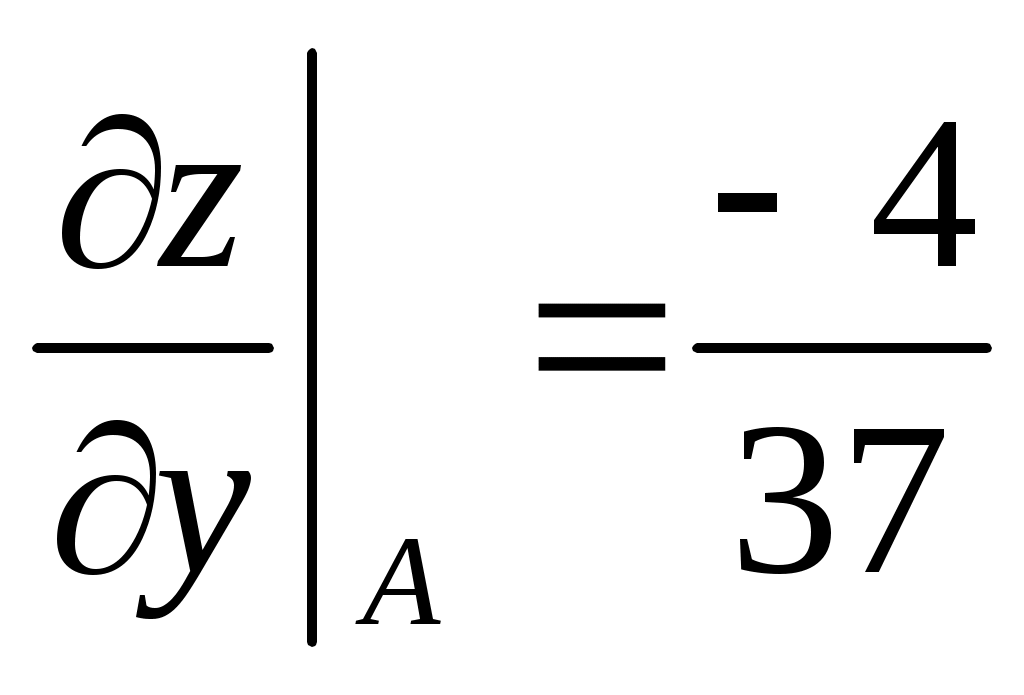 ; ;
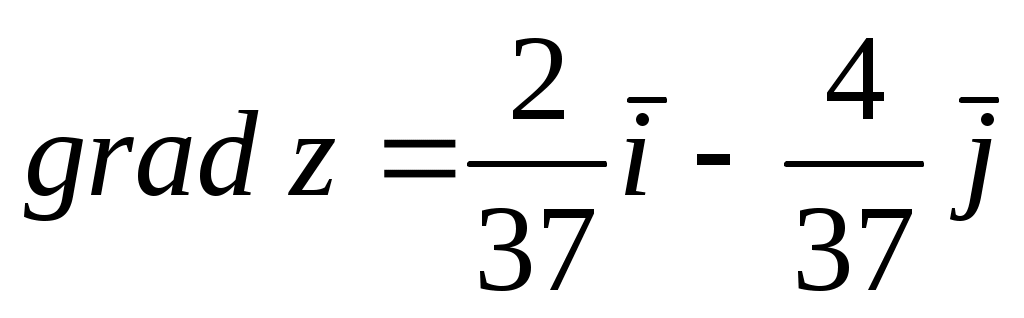 (использовалась формула (использовалась формула 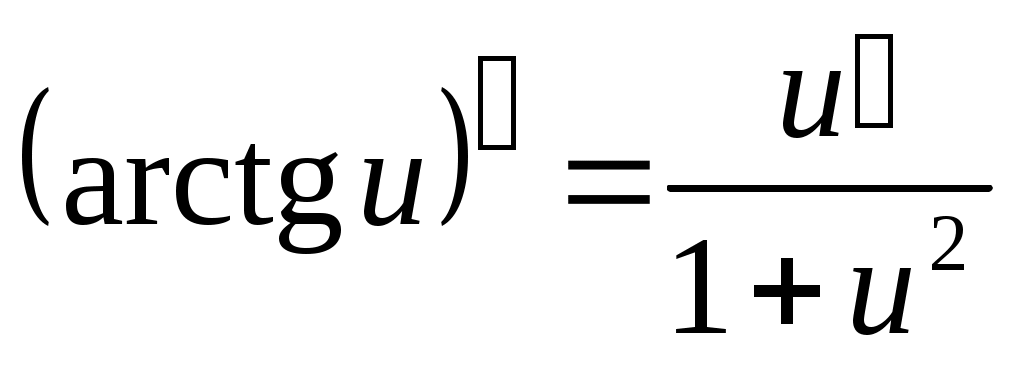 ). ).
Производная по заданному направлению вектора 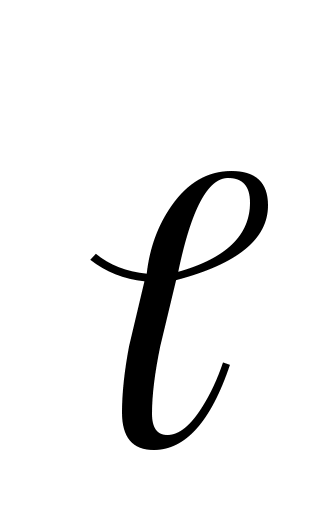 находятся по формуле находятся по формуле 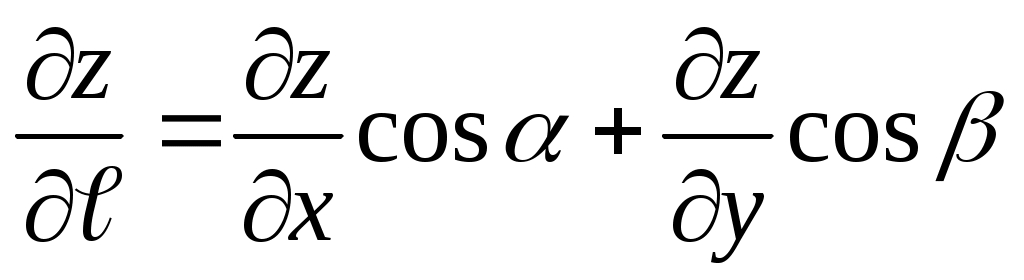 , где , где 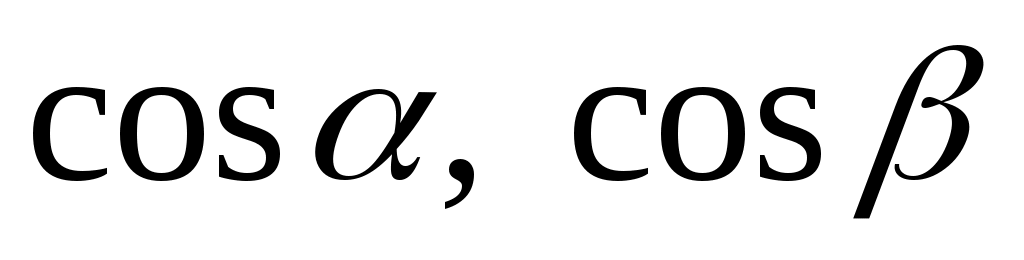 – направляющие косинусы вектора – направляющие косинусы вектора 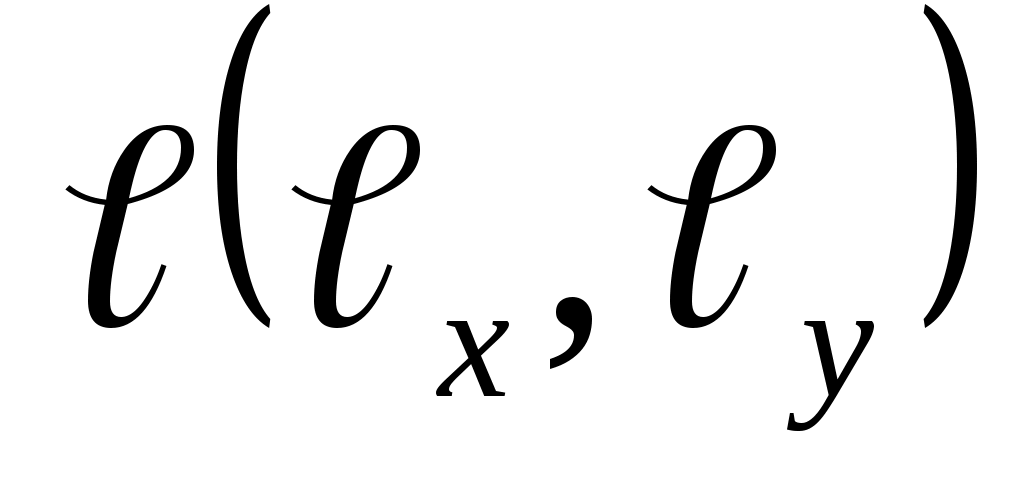 , , 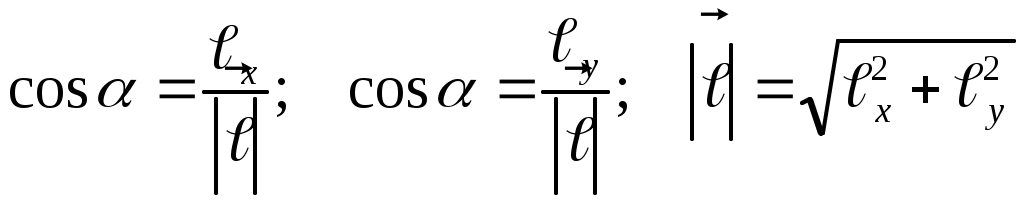 . .
Пример: Дана функция 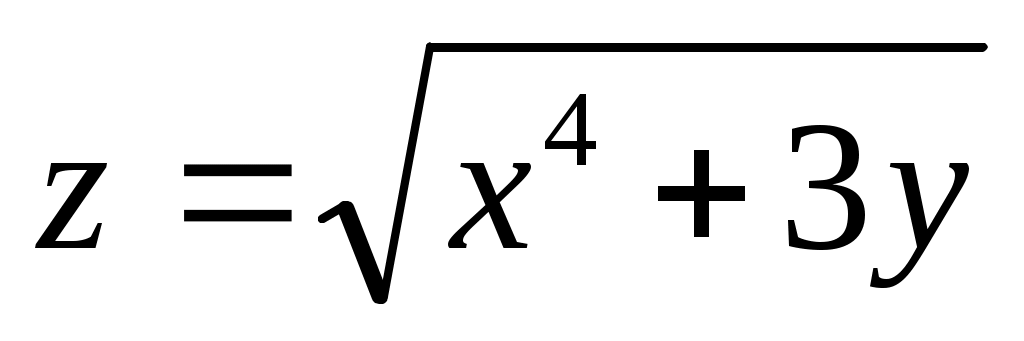 . Найти производную по направлению вектора . Найти производную по направлению вектора 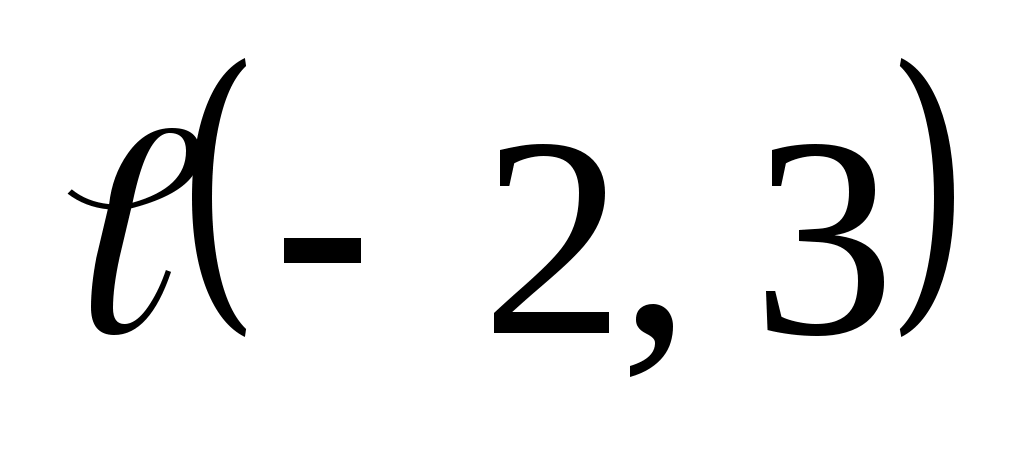 в точке в точке 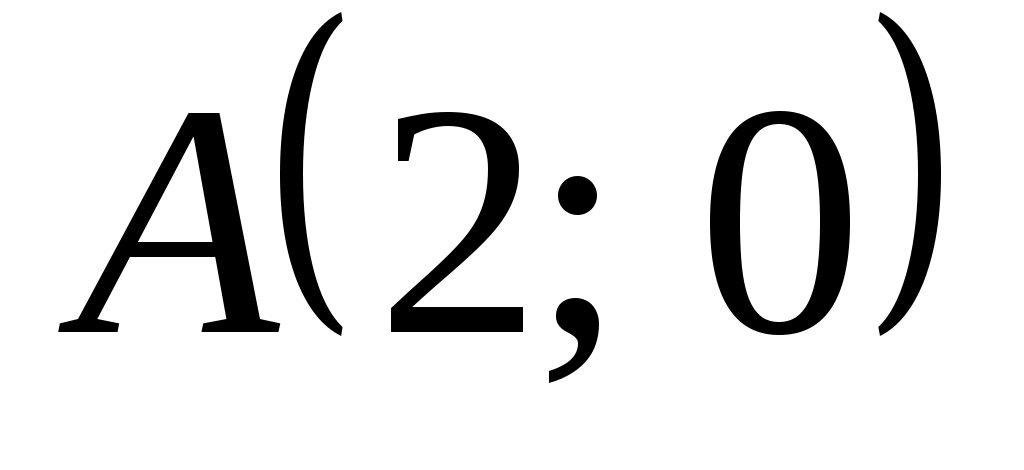 . .
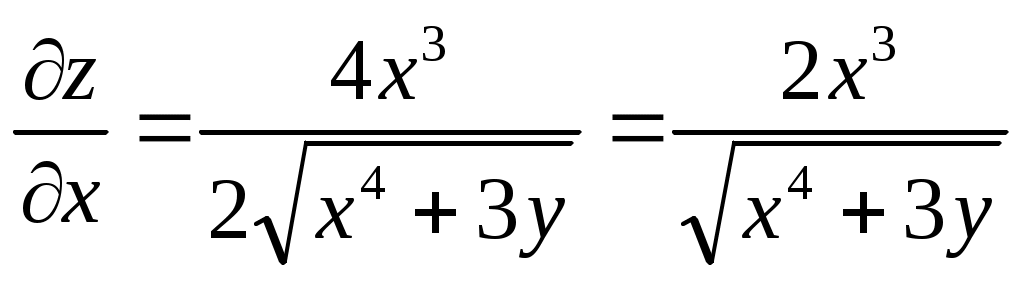 ; ; 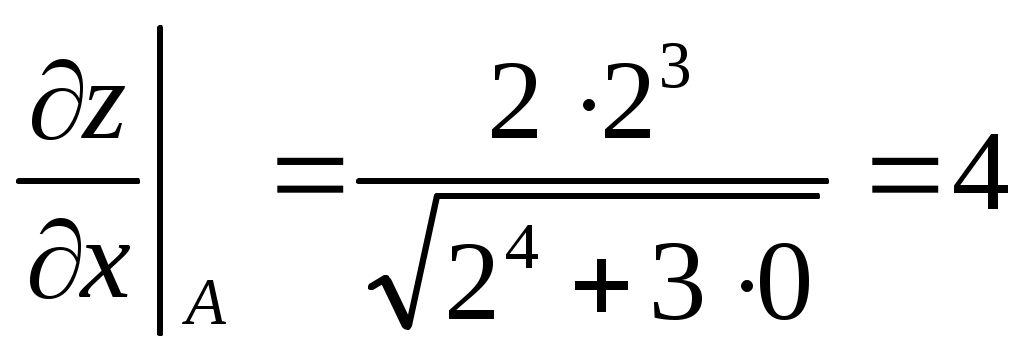 ; ;
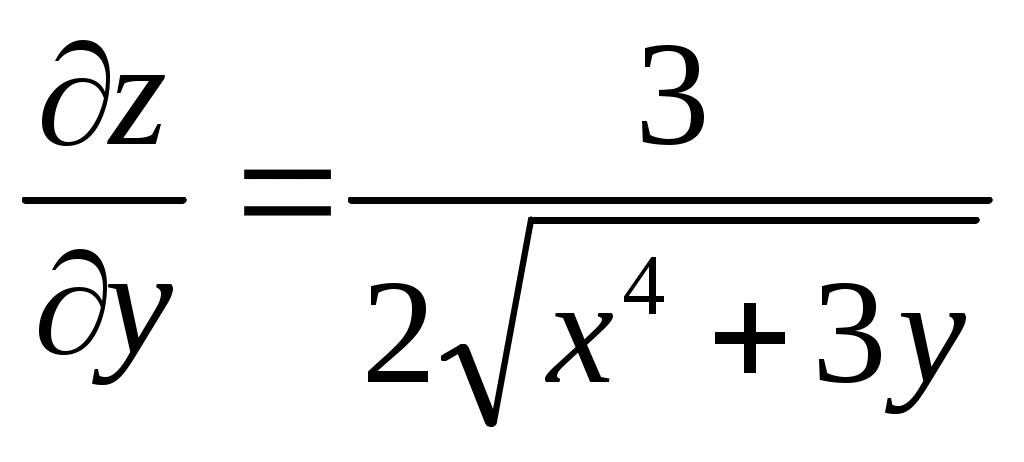 ; ; 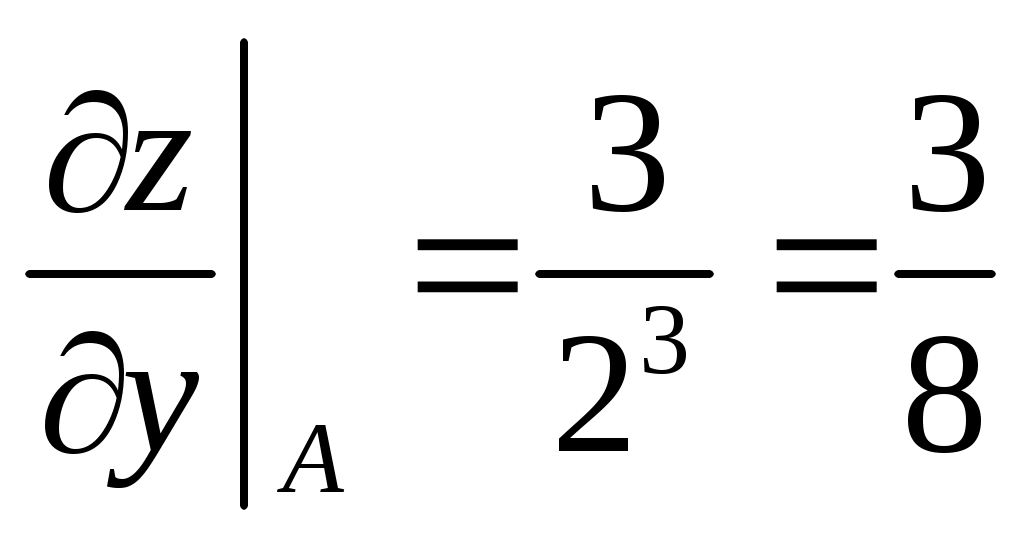 (использовалась формула (использовалась формула 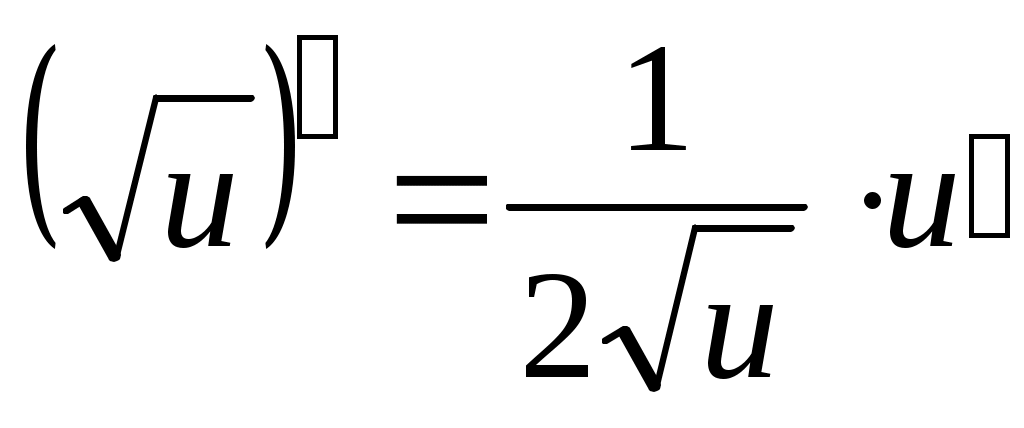 ). ).
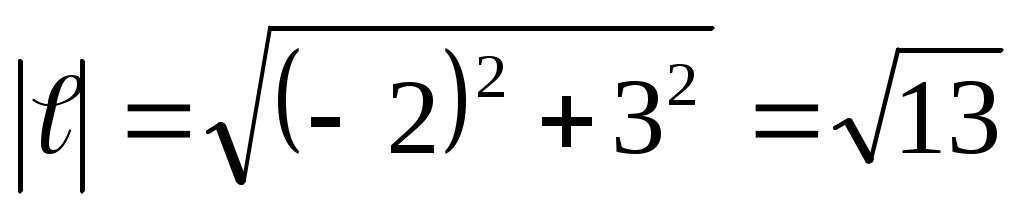 ; ; 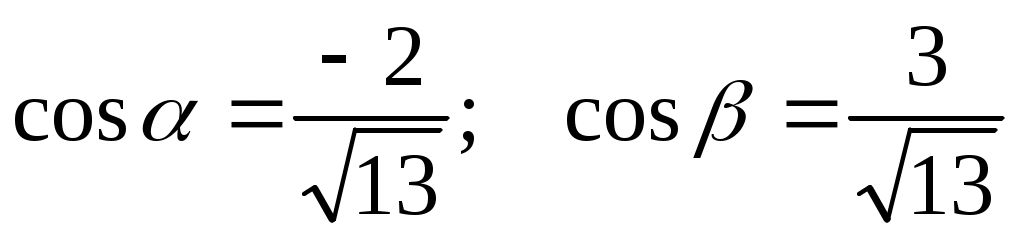 ; ;
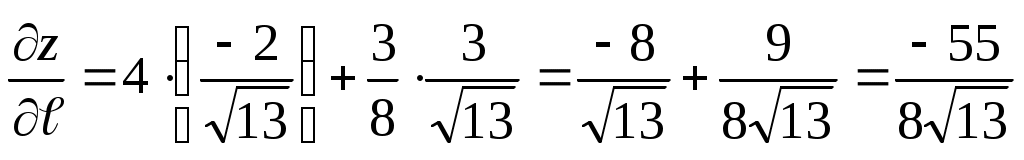 . .
ЗАДАНИЯ (только четные №)
Задание 1. Даны две функции 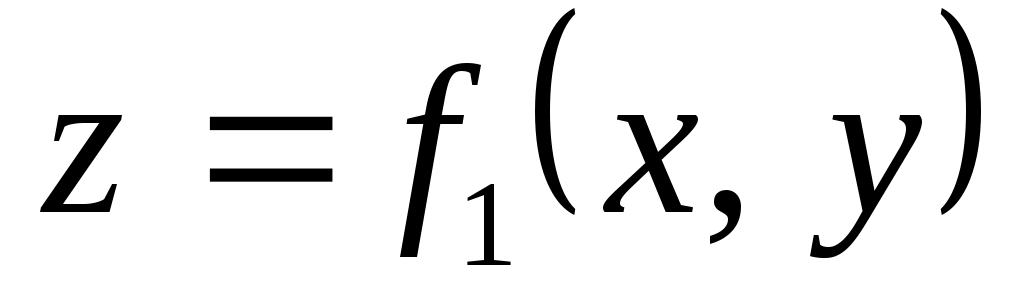 и и 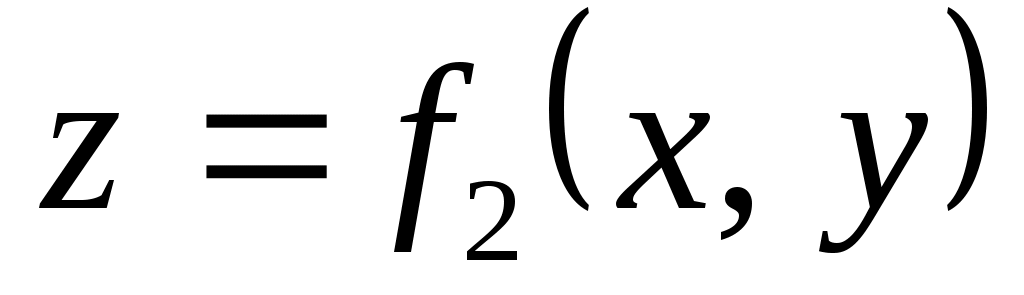 . Для каждой функции проверить равенство смешанных производных второго порядка . Для каждой функции проверить равенство смешанных производных второго порядка 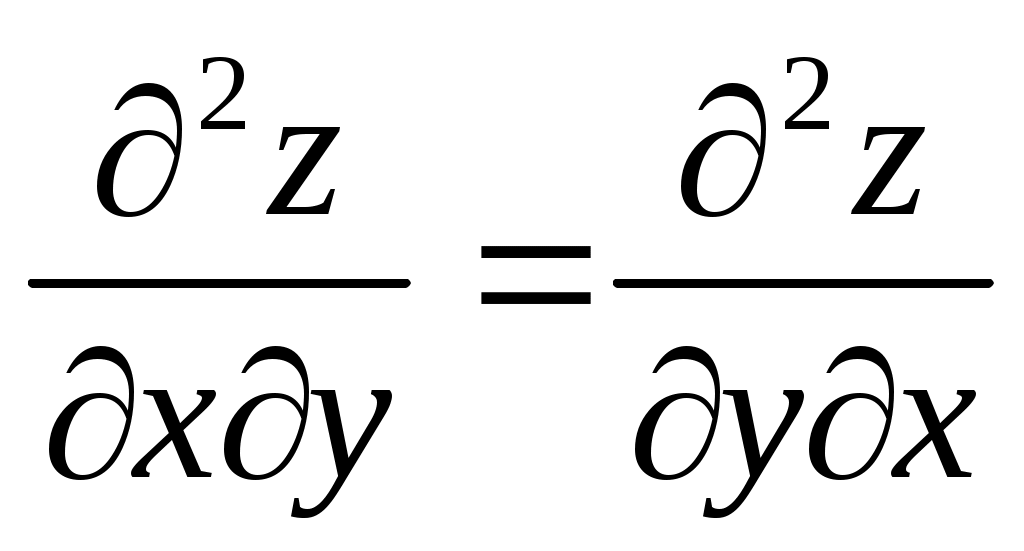 . .
Задание 2. Даны: функция 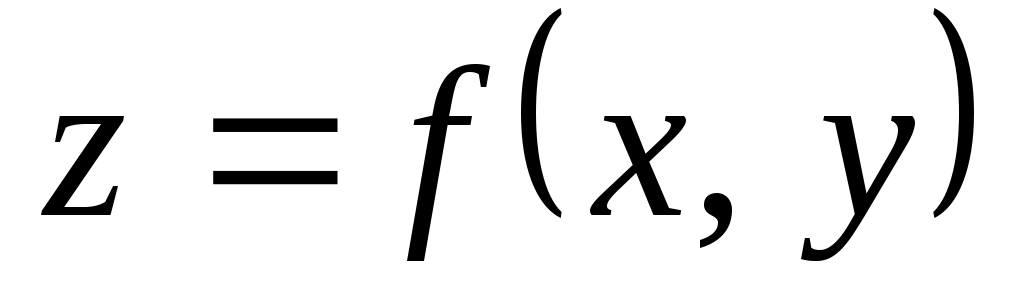 , точка , точка 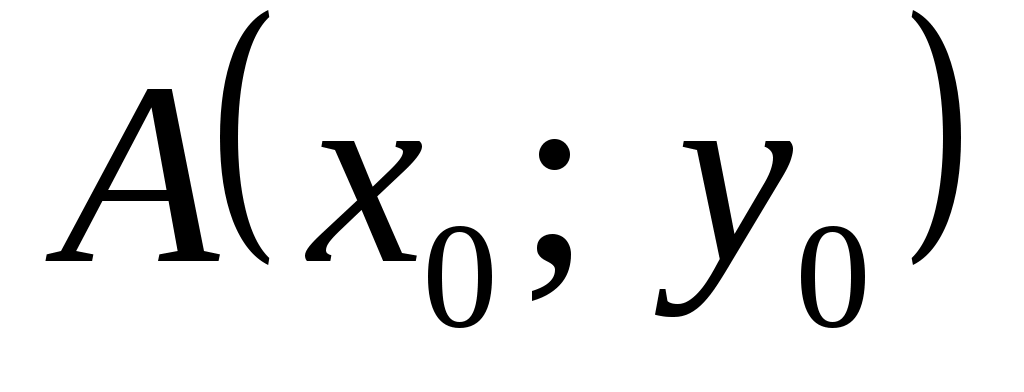 и вектор и вектор 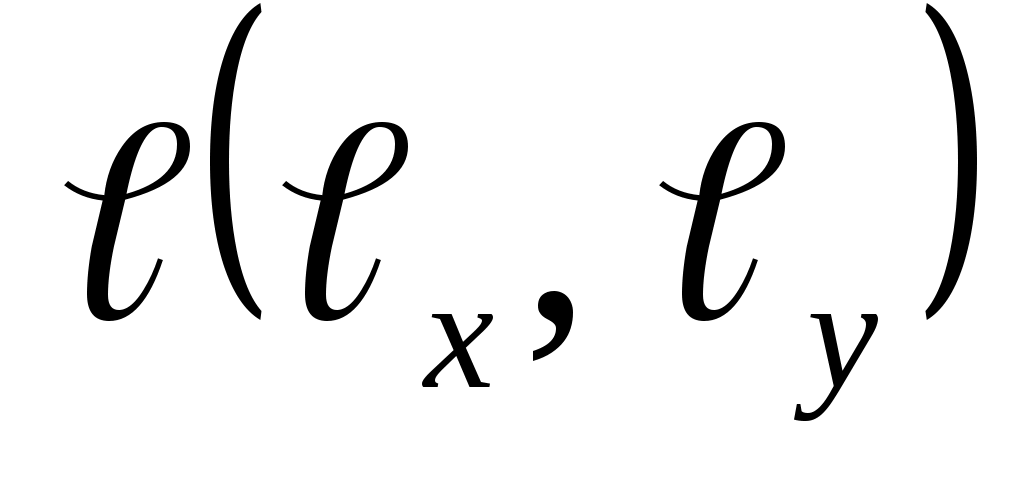 . Найти: 1) . Найти: 1) 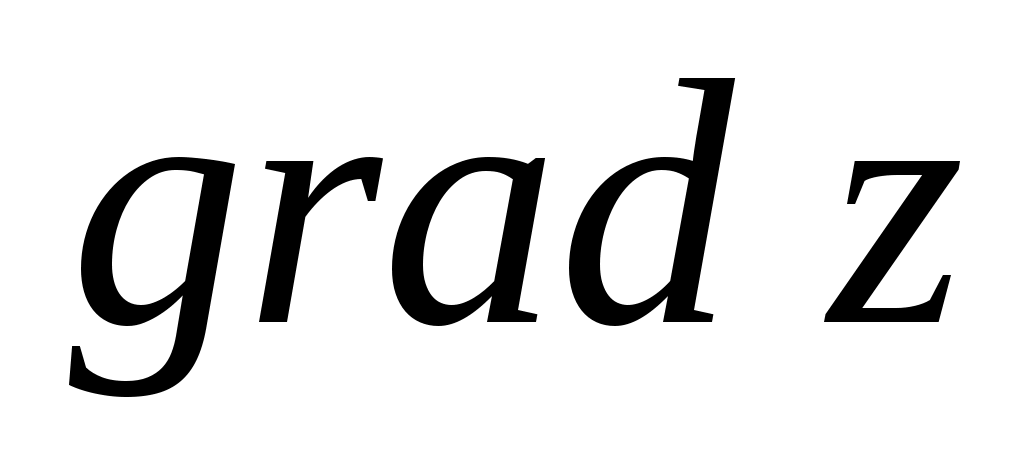 в точке А; 2) производную по направлению вектора в точке А; 2) производную по направлению вектора 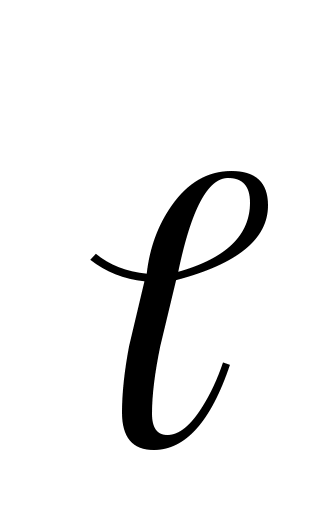 в точке А. в точке А.
№
вар-та
|
Задания
|
1
|
1) 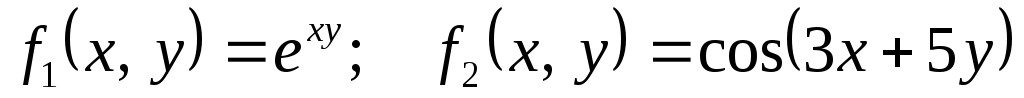 ; ;
2) 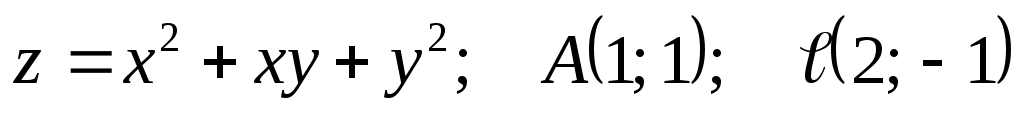 . .
|
2
|
1) 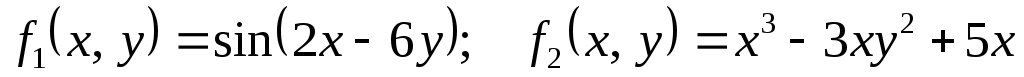 ; ;
2) 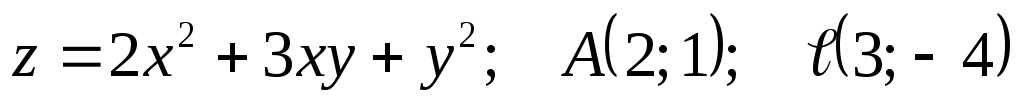 . .
|
3
|
1) 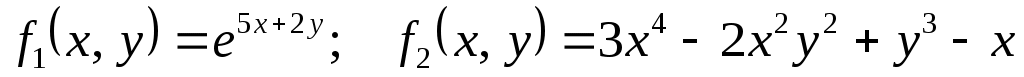 ; ;
2) 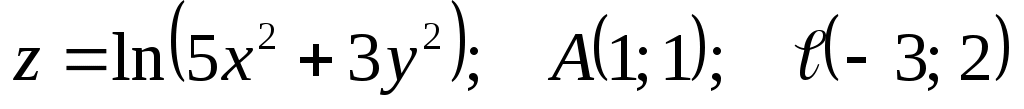 . .
|
4
|
1) 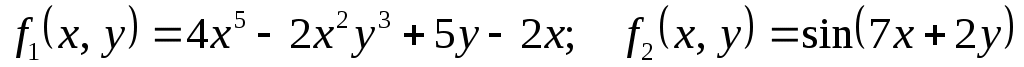 ; ;
2) 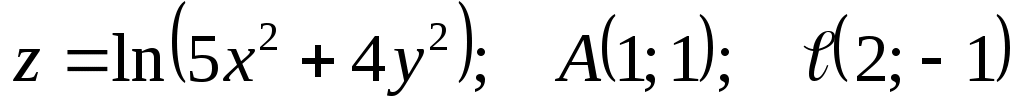 . .
|
5
|
1) 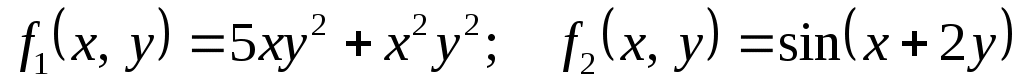 ; ;
2) 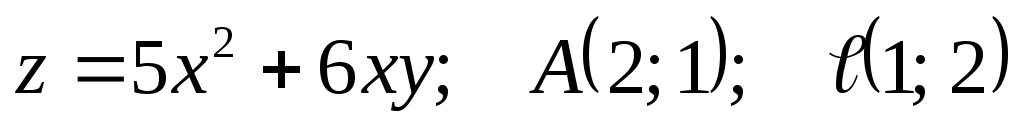 . .
|
6
|
1) 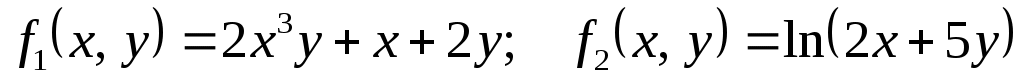 ; ;
2)  . .
|
7
|
1) 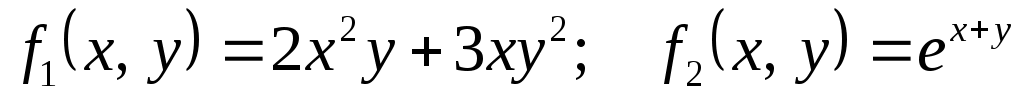 ; ;
2) 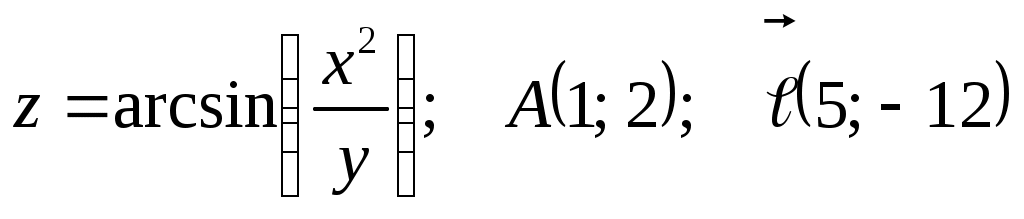 . .
|
8
|
1) 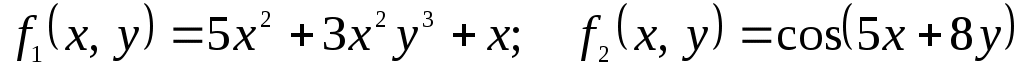 ; ;
2) 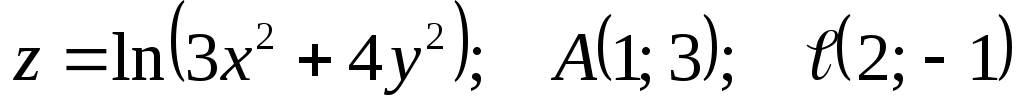 . .
|
9
|
1) 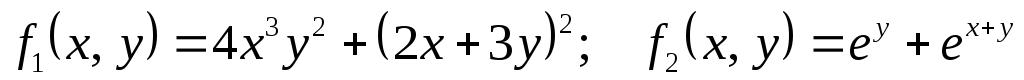 ; ;
2) 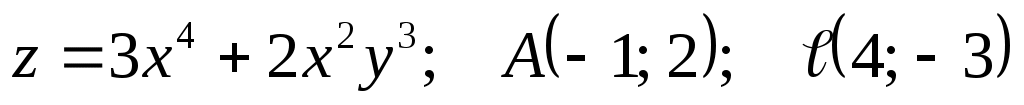 . .
|
10
|
1) 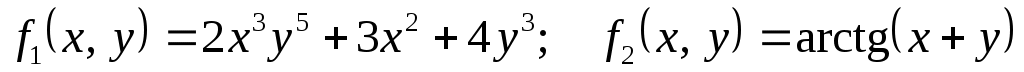 ; ;
2) 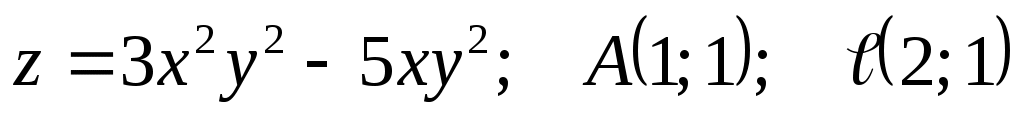 . .
|
Тема: «Дифференциальные уравнения»
Краткая теория и методические указания для решения:
Дифференциальные уравнения I порядка: 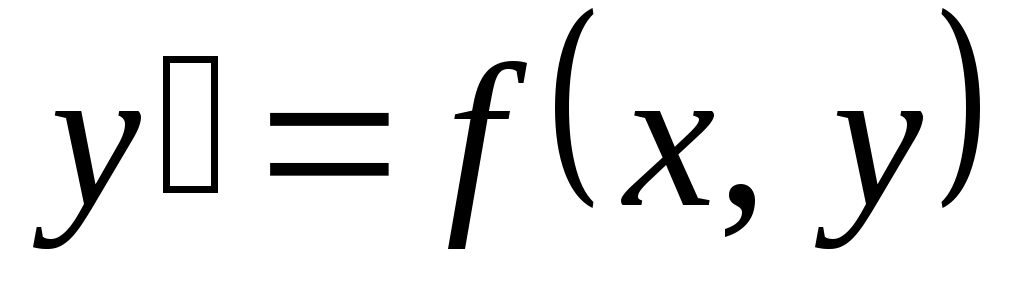 или или 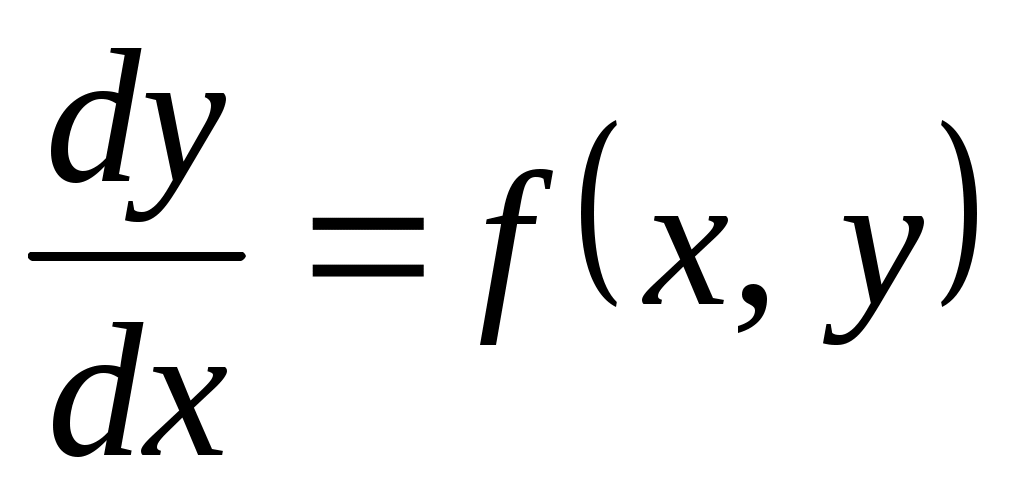 . Общее решение – это совокупность решений . Общее решение – это совокупность решений 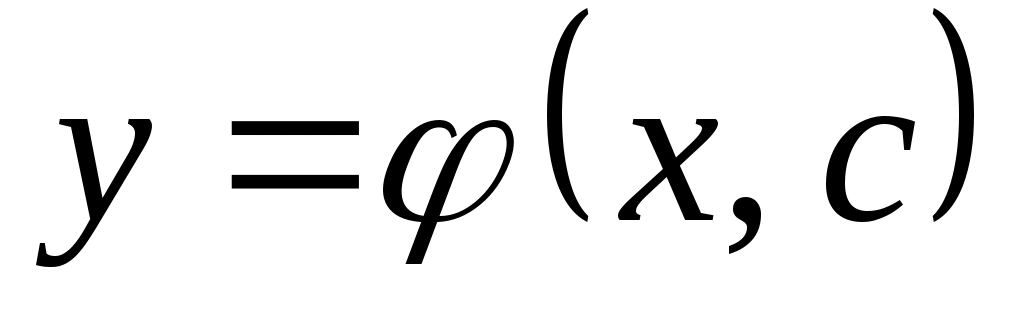 или или 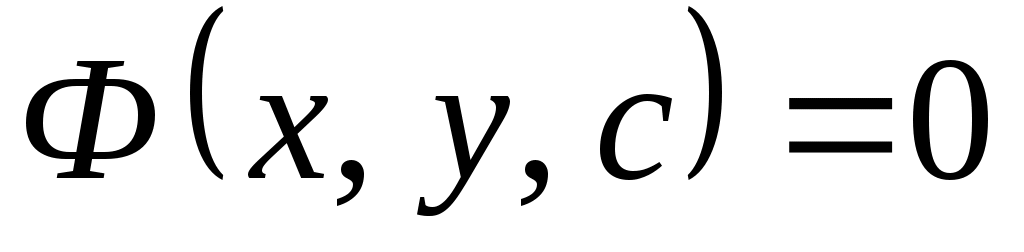 , зависящих от произвольной постоянной С. , зависящих от произвольной постоянной С.
Виды и методы решения некоторых дифференциальных уравнений I порядка:
Уравнения с разделяющимися переменными 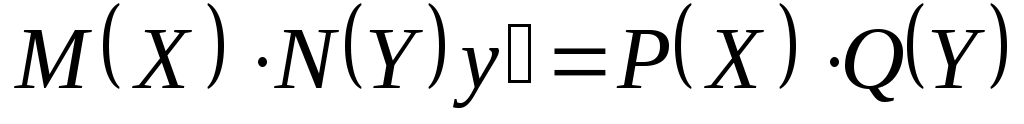
Алгоритм решения:
а) 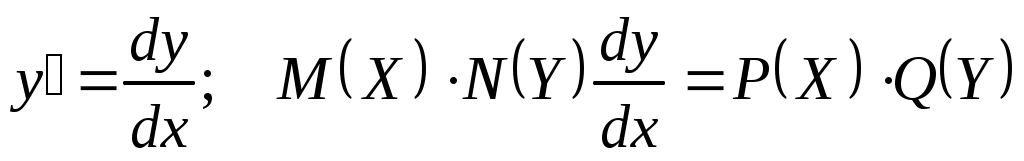 ; Умножим на ; Умножим на 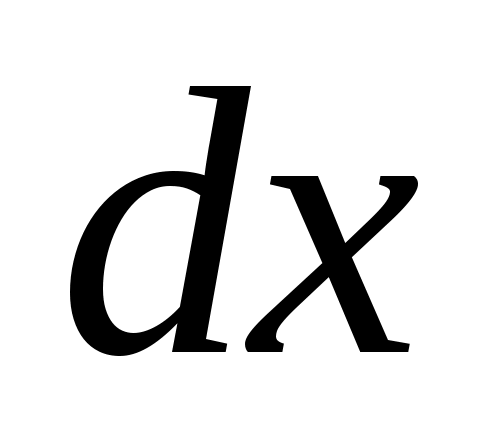 обе части уравнения. Получим б) обе части уравнения. Получим б) 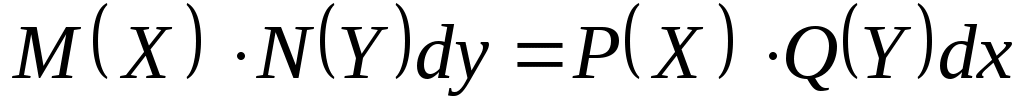 ; ;
в) Разделим переменные, чтобы слева были функции, зависящие от у, а справа – от х. Для этого разделим обе части уравнения на 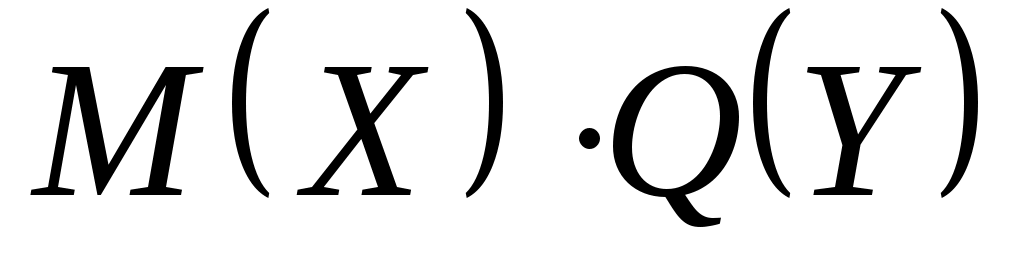 . Получим . Получим 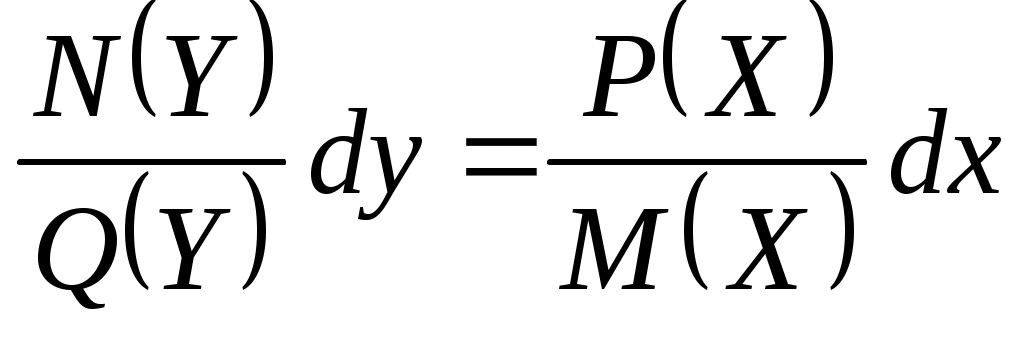 ; ;
г) Произведя интегрирование (слева по 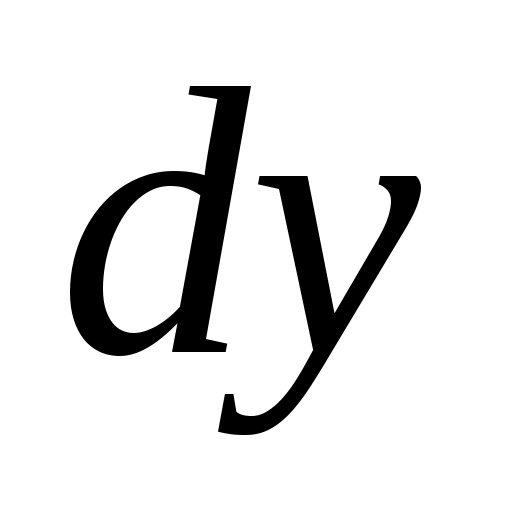 , справа по , справа по 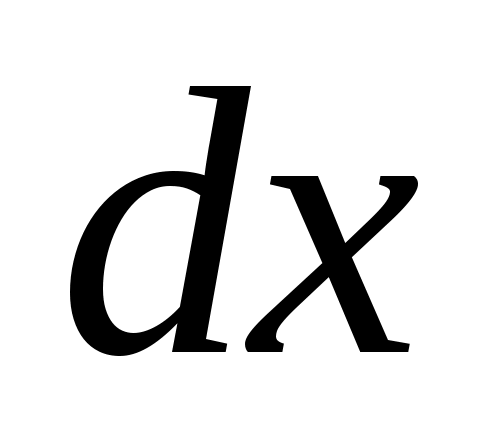 ) получим решение ) получим решение
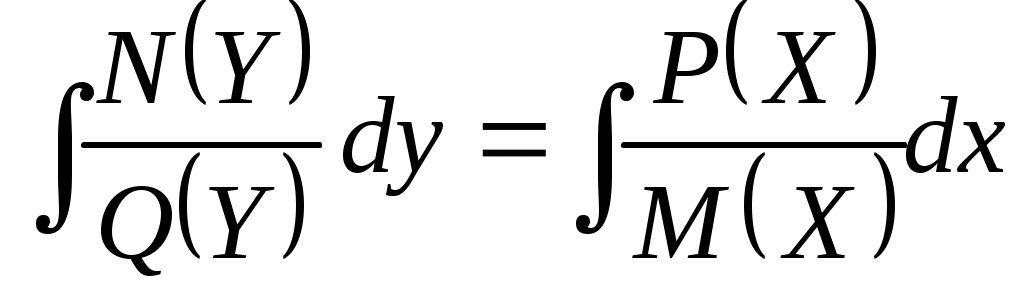 . .
Линейные дифференциальные уравнения I порядка 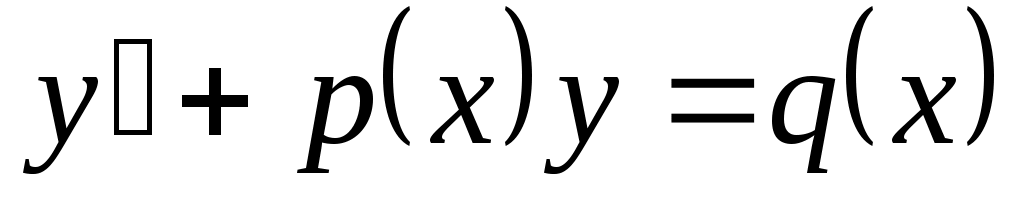 ( (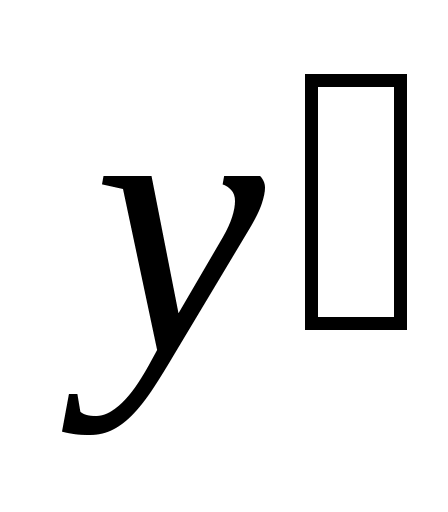 и у входят в первой степени). Методом Бернулли заменой и у входят в первой степени). Методом Бернулли заменой 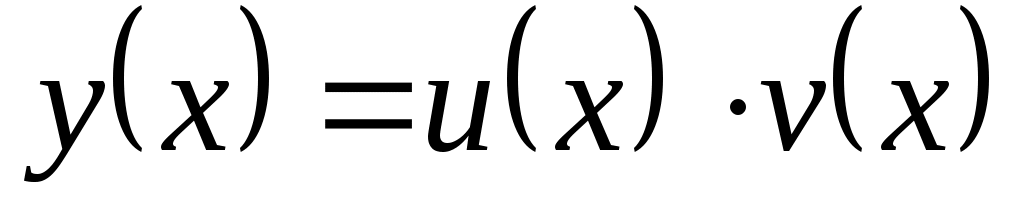 приводим к последовательному решению двух уравнений с разделяющимися переменными относительно приводим к последовательному решению двух уравнений с разделяющимися переменными относительно 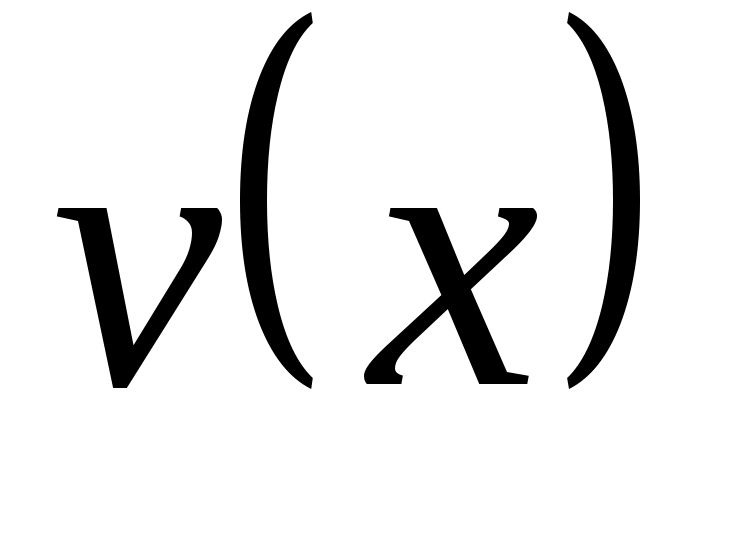 и затем и затем 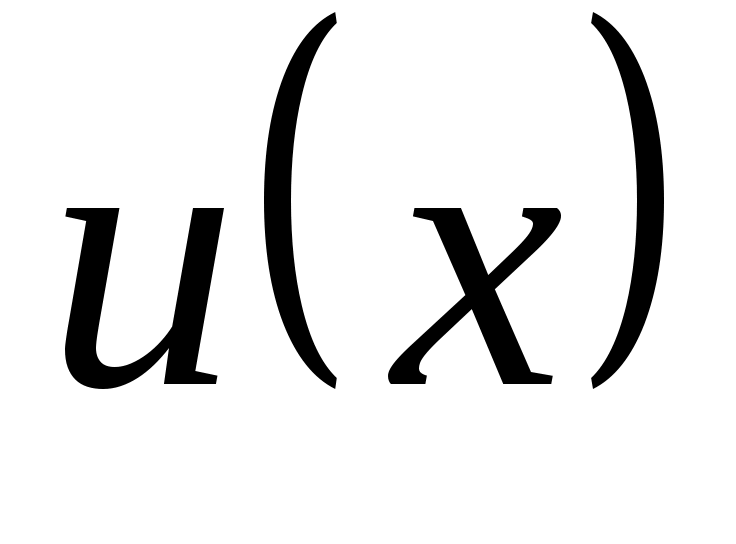 . . 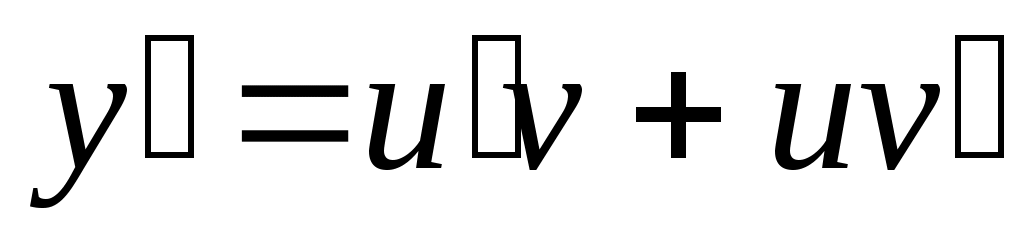 . Подставим в уравнение: . Подставим в уравнение: 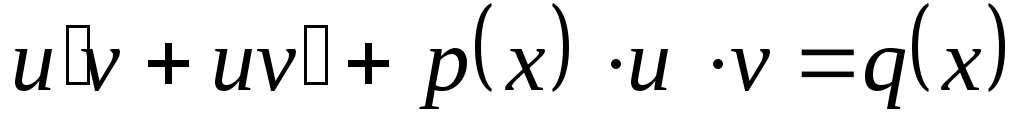 или или 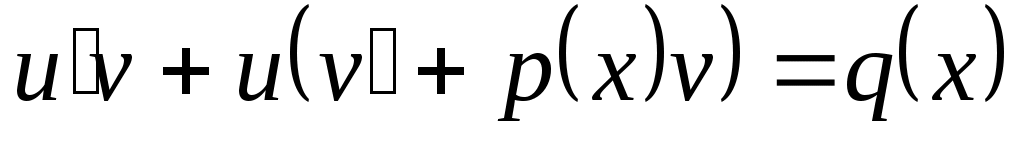 (1.2.1) . Определим (1.2.1) . Определим 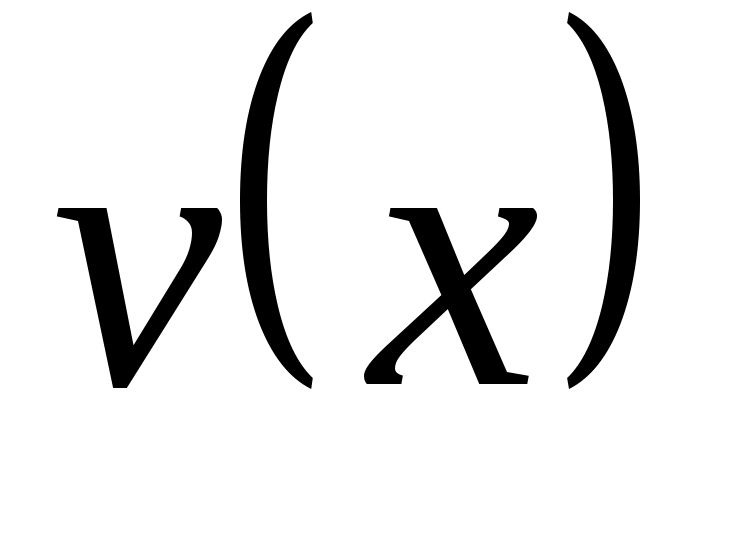 таким образом: таким образом: 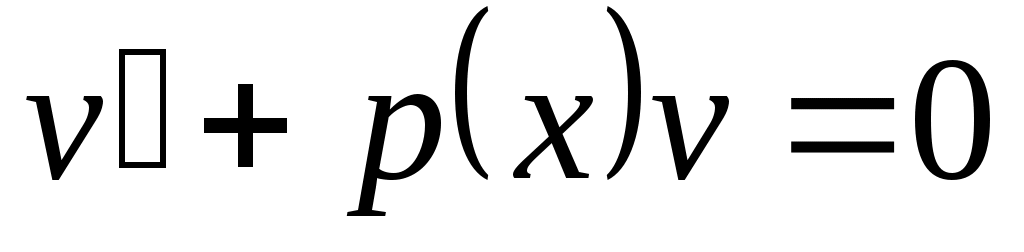 . Решив это уравнение, одно частное решение . Решив это уравнение, одно частное решение 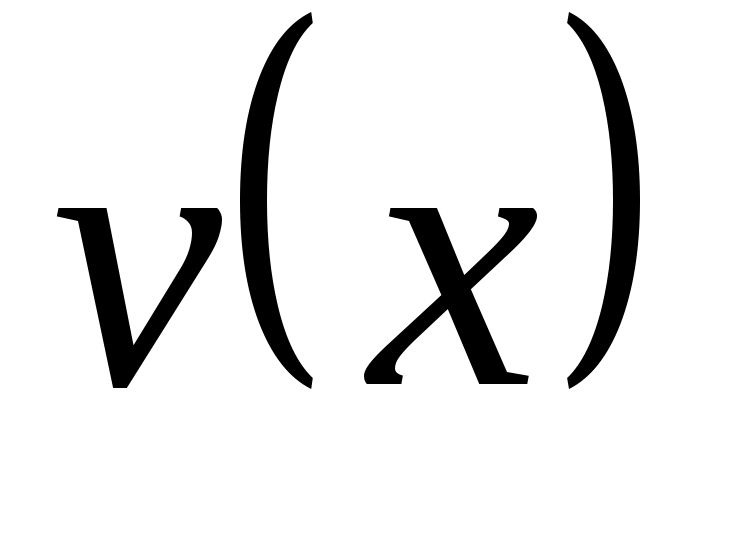 подставим в (1.2.1) . Получим уравнение относительно подставим в (1.2.1) . Получим уравнение относительно 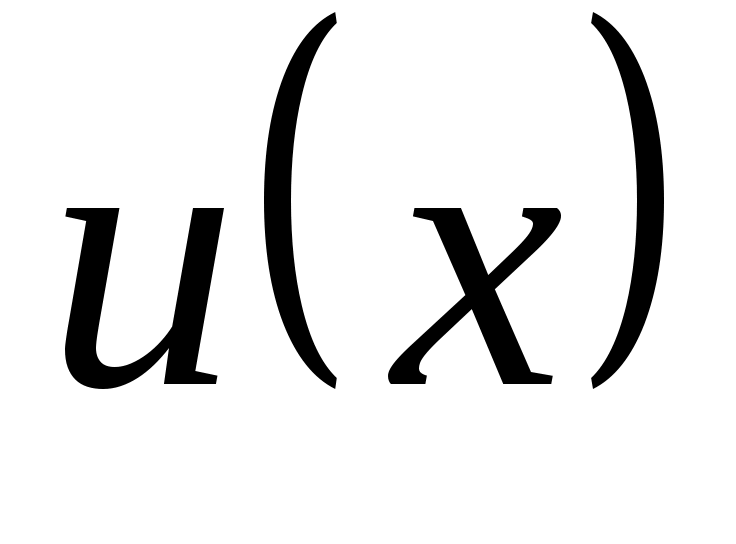 : : 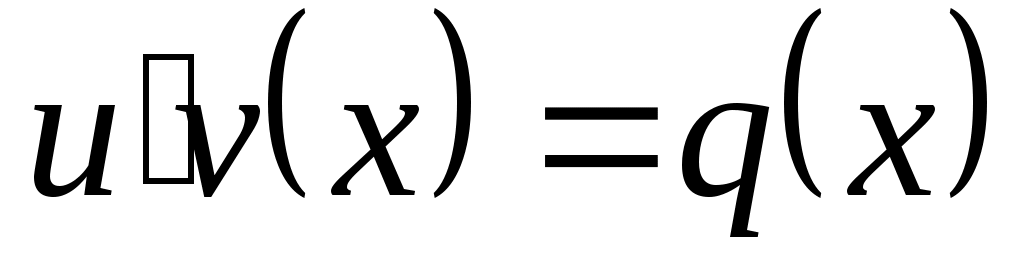 . Определим общее решение . Определим общее решение 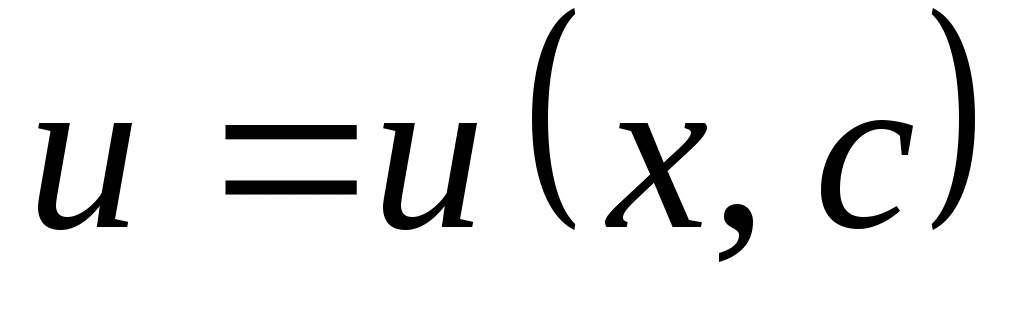 . Общее решение уравнения 1.2 есть . Общее решение уравнения 1.2 есть 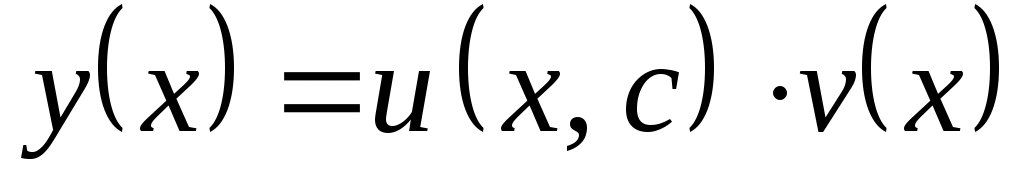 . .
Дифференциальные уравнения II порядка. 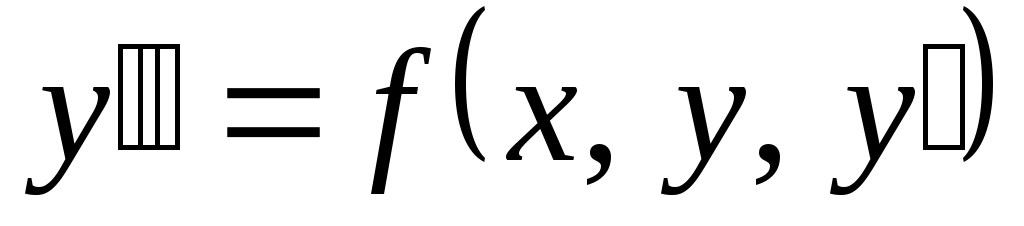 . Общее решение – это совокупность решений вида . Общее решение – это совокупность решений вида 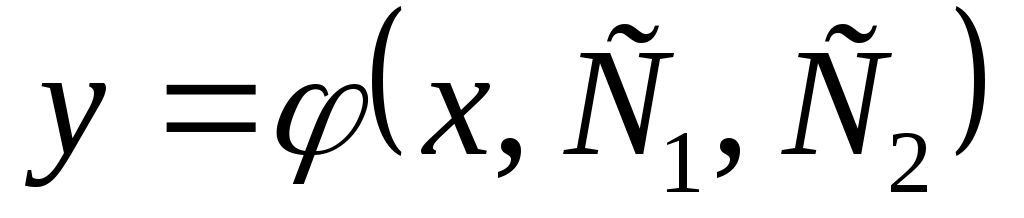 , где , где 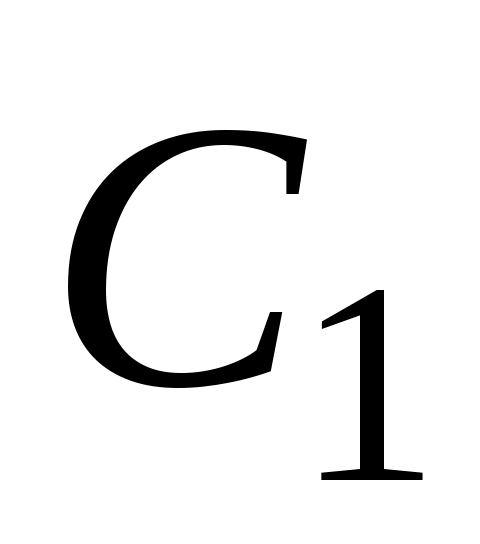 и и 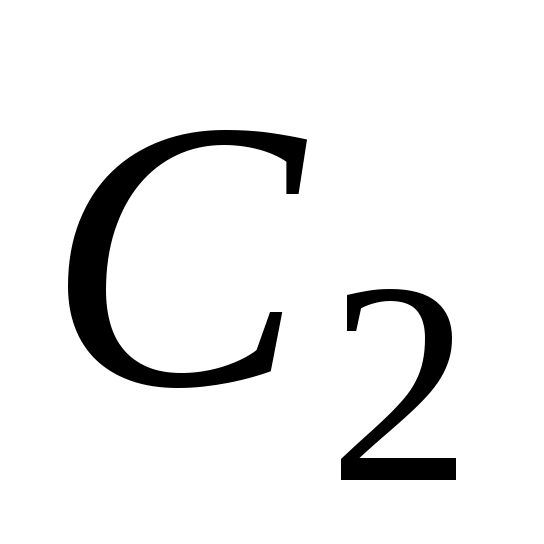 – произвольные постоянные. – произвольные постоянные.
2.1 Дифференциальные линейные уравнения II порядка с постоянными коэффициентами. 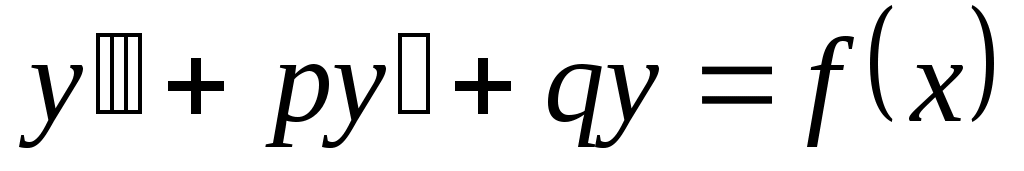 , , 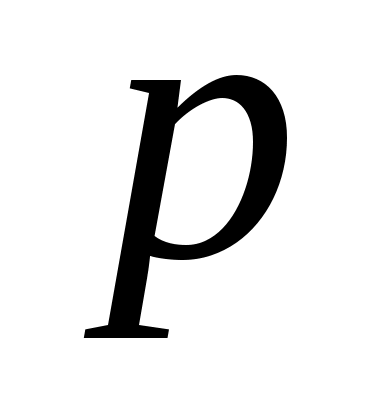 и и 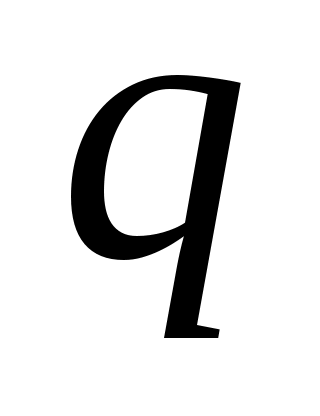 – постоянные числа. Если – постоянные числа. Если 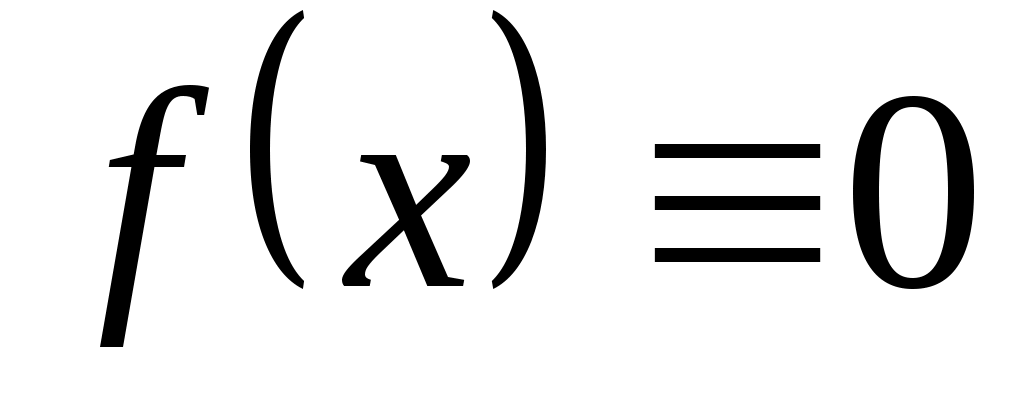 , то уравнение называется однородным, если , то уравнение называется однородным, если 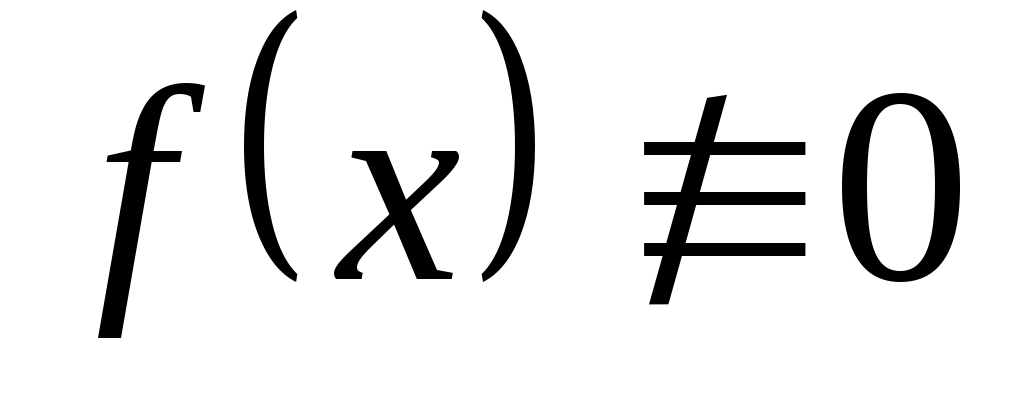 , то неоднородным. , то неоднородным.
Общее решение неоднородного уравнения 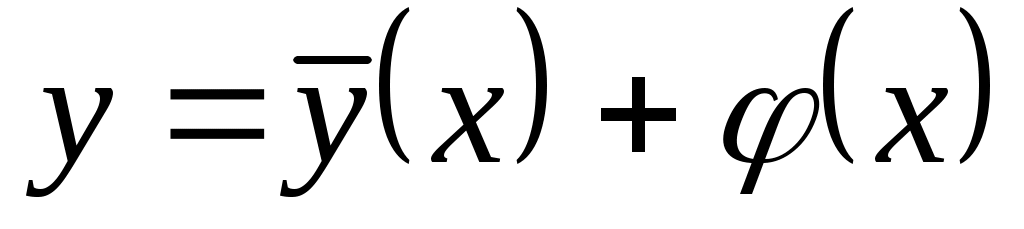 , где , где 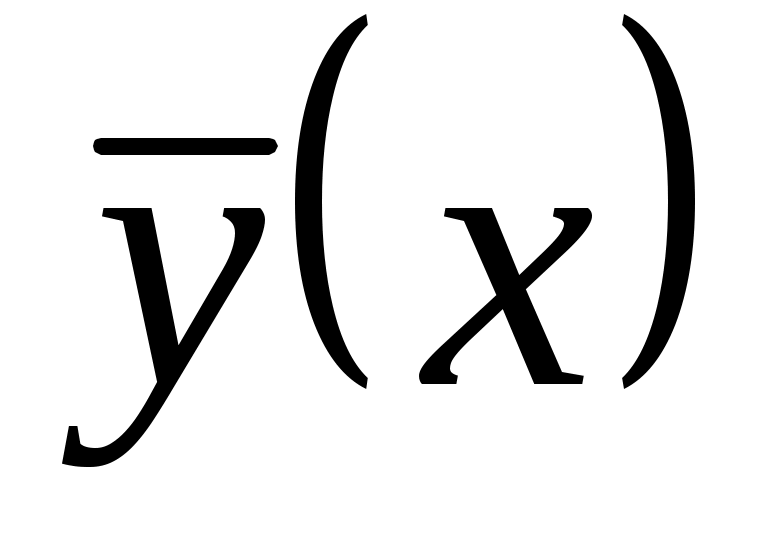 – общее решение однородного уравнения, – общее решение однородного уравнения, 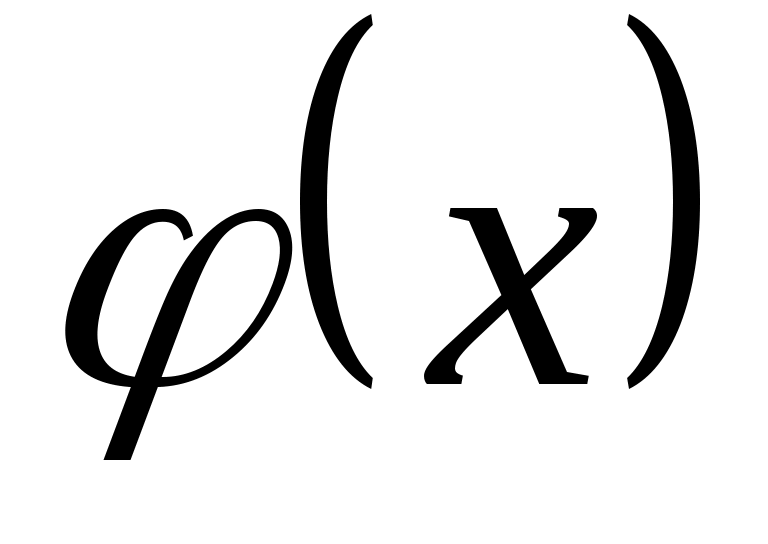 – какое-нибудь частное решение неоднородного уравнения. – какое-нибудь частное решение неоднородного уравнения.
2.1.1. Решение однородного линейного уравнения II порядка
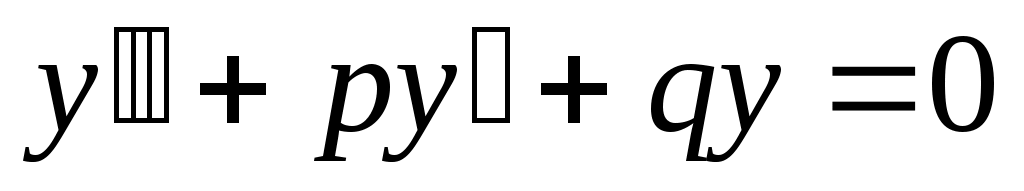
Составим и решим характеристическое уравнение 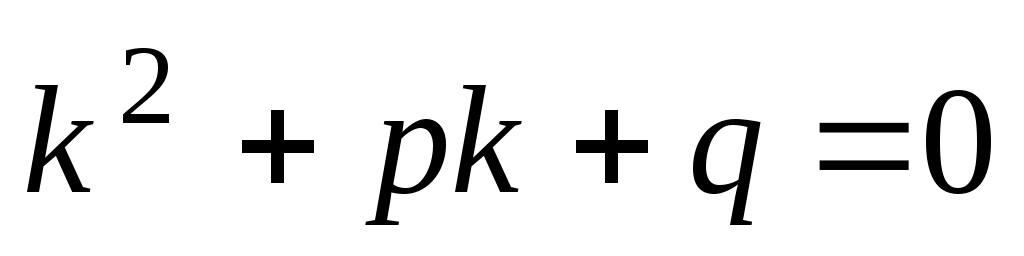 . .
Дискриминант 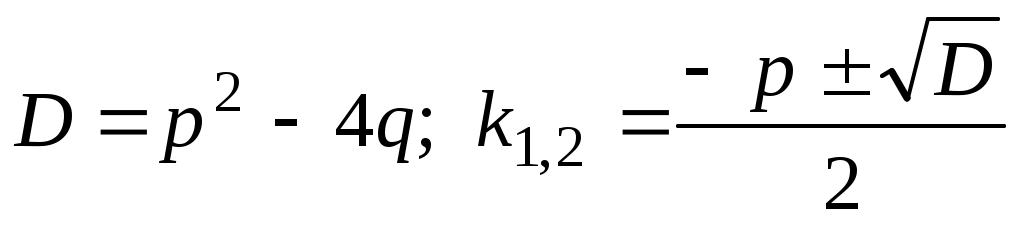 . .
Могут быть 3 случая:
а)  , два разных действительных корня , два разных действительных корня 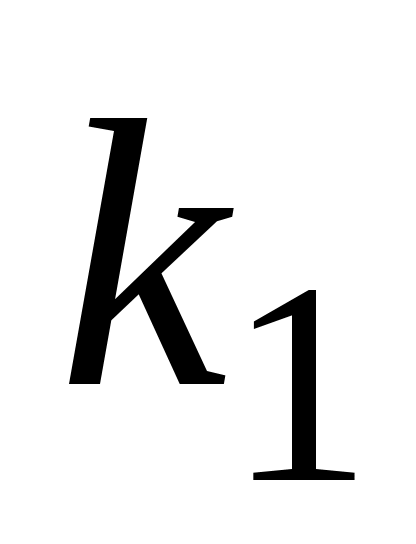 и и 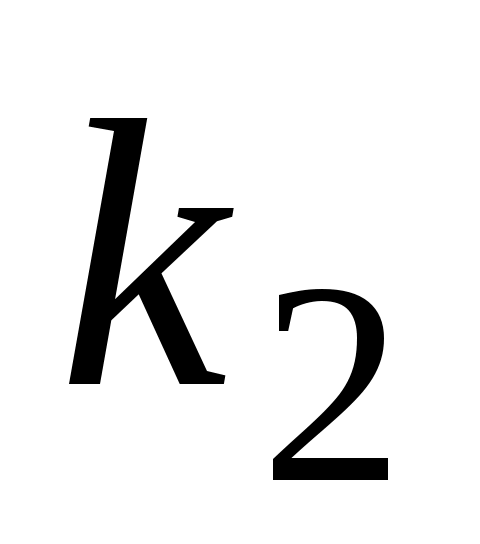 , , 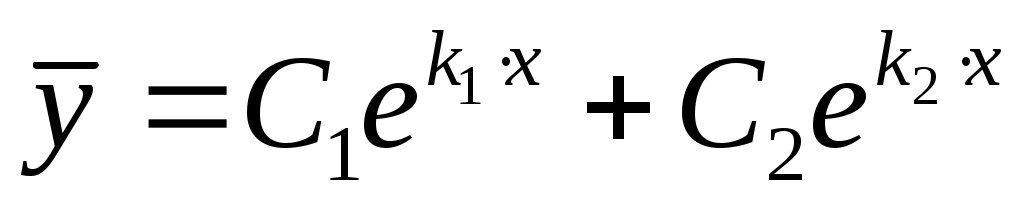 ; ;
б) 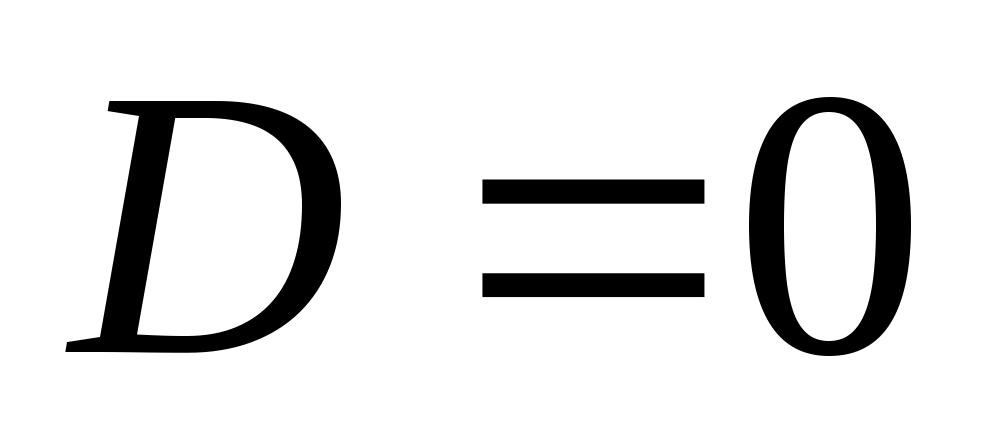 , два равных действительных корня: , два равных действительных корня: 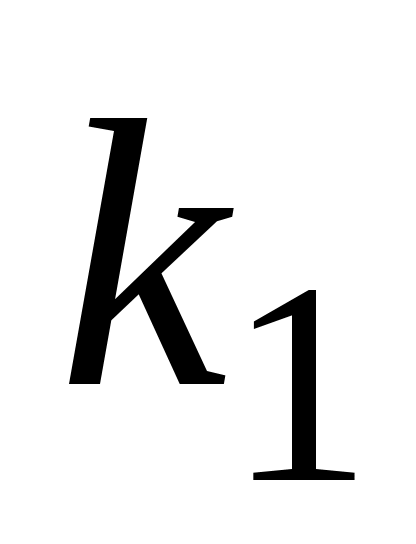 = = 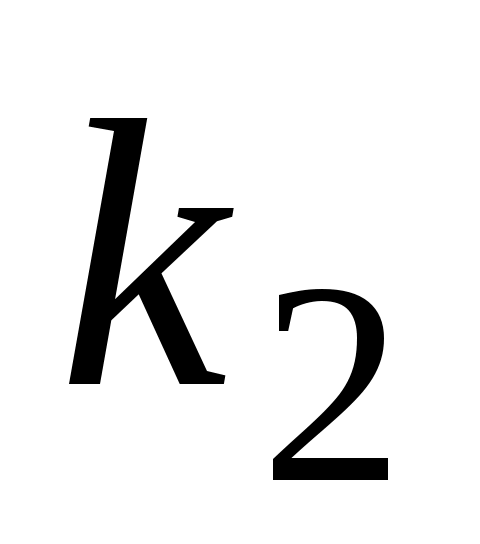 , , 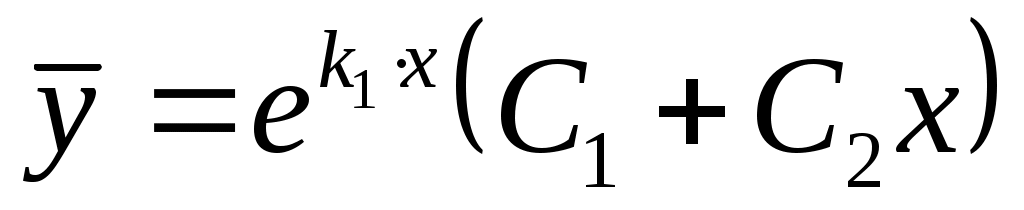 ; ;
в) 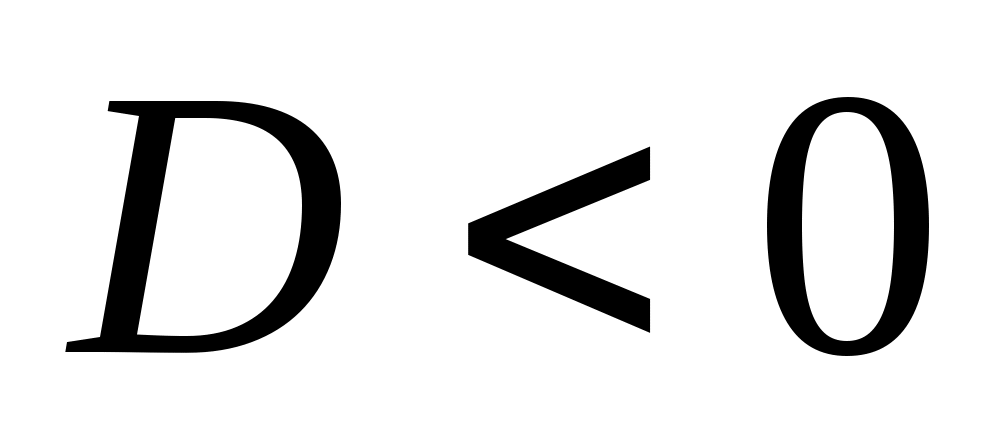 , два комплексных корня: , два комплексных корня: 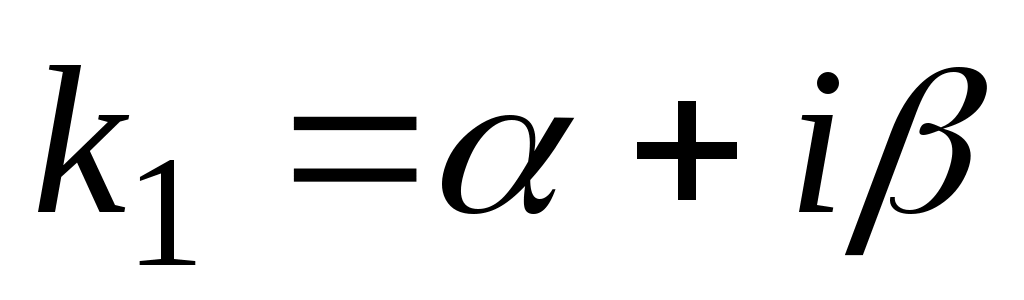 и и 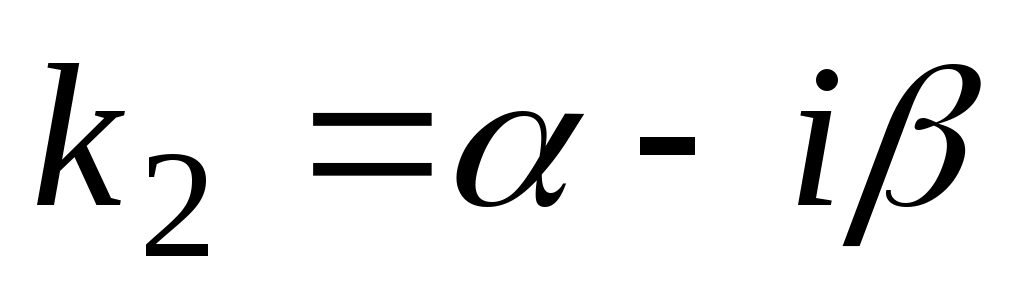 , , 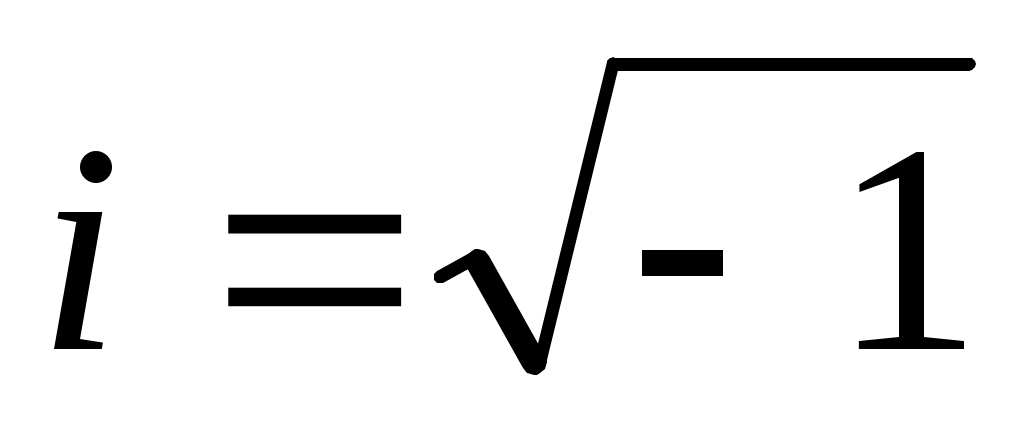 – мнимая единица, – мнимая единица, 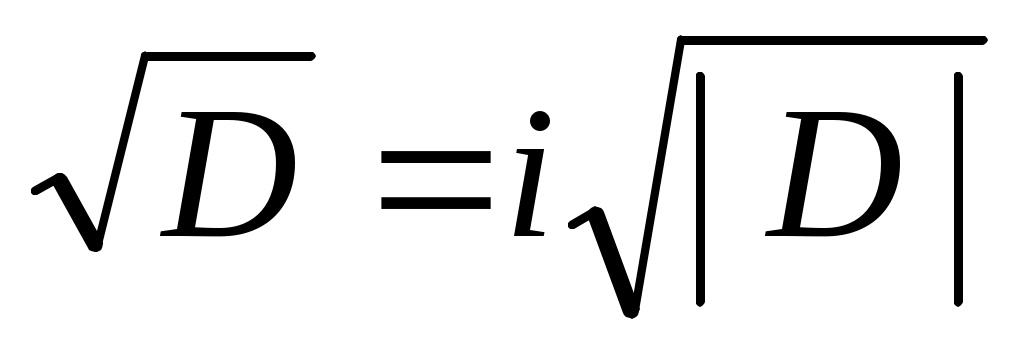 , ,  – действительная, – действительная, 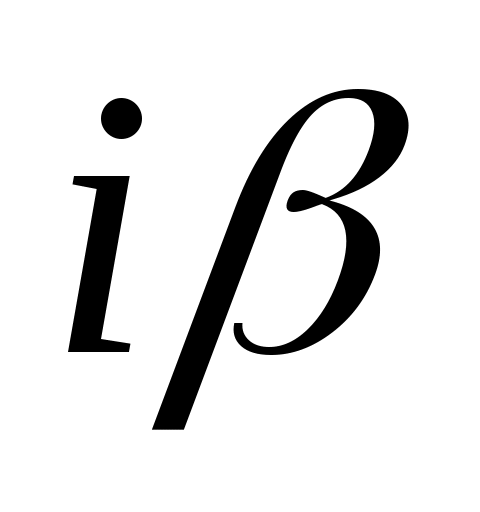 – мнимая часть комплексного числа; – мнимая часть комплексного числа; 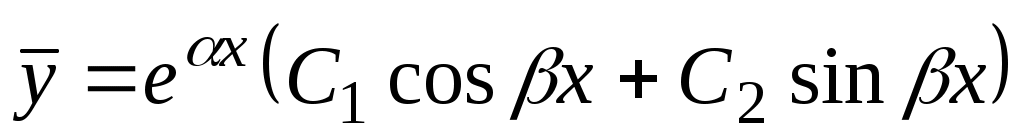 . Если . Если 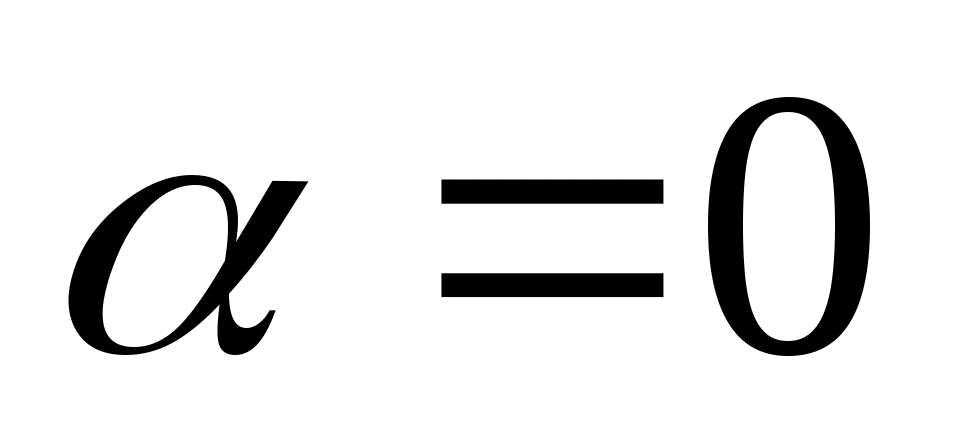 , , 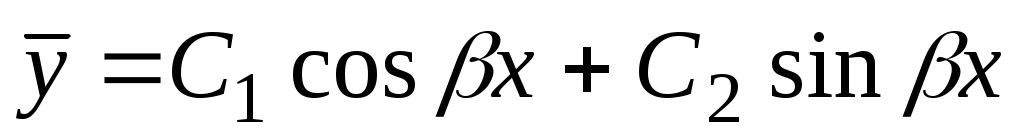 . .
2.1.2. Нахождение частного решения неоднородного уравнения 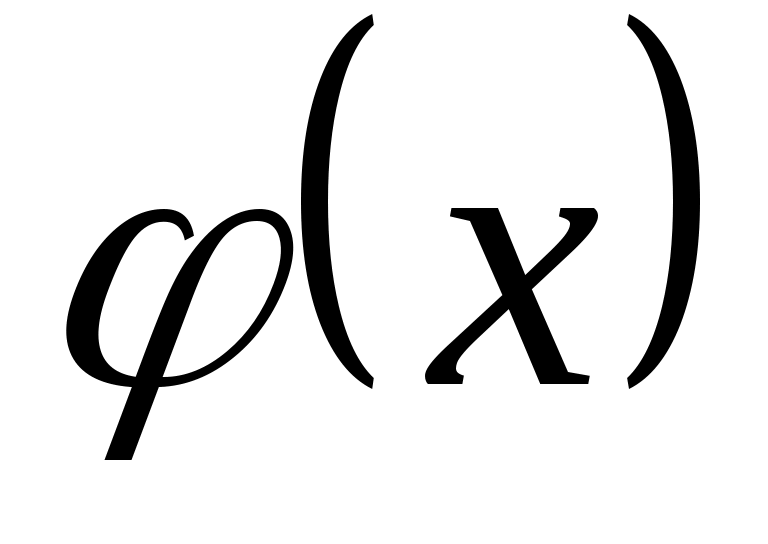 методом неопределённых коэффициентов в зависимости от вида правой части уравнения методом неопределённых коэффициентов в зависимости от вида правой части уравнения 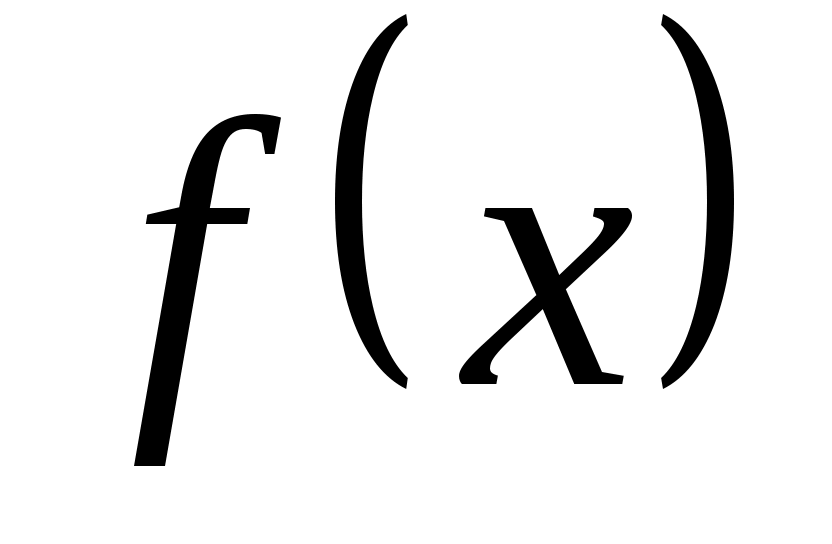 . .
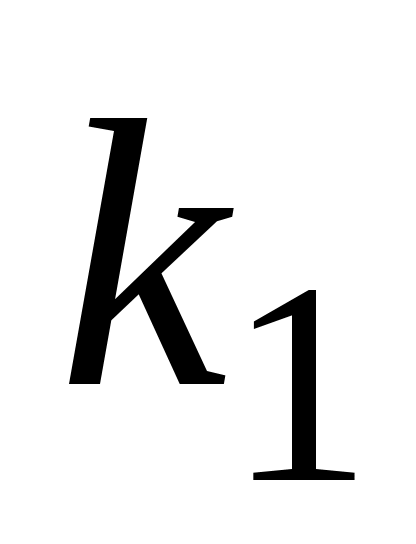 и и 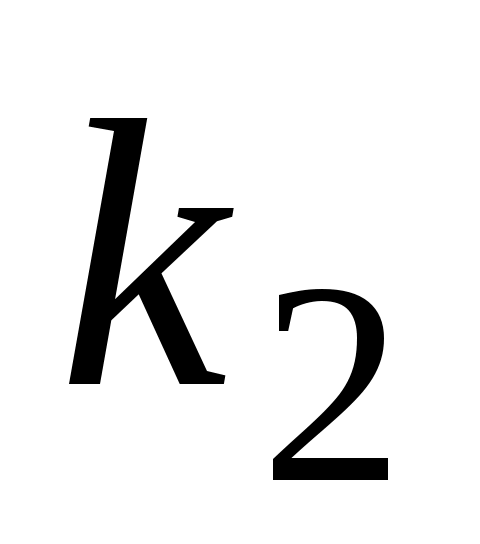 – корни характеристического уравнения. – корни характеристического уравнения.
2.1.2.1. 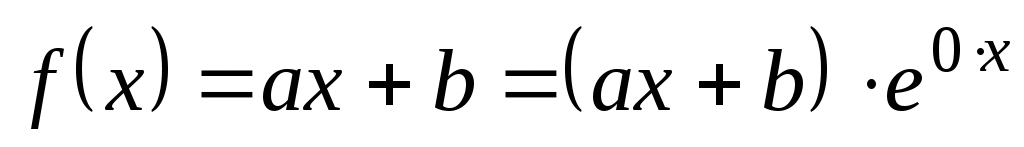 (а и (а и 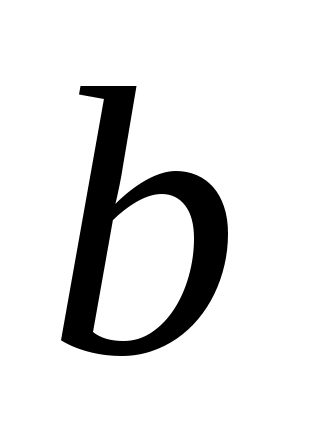 – данные числа) – данные числа)
а) 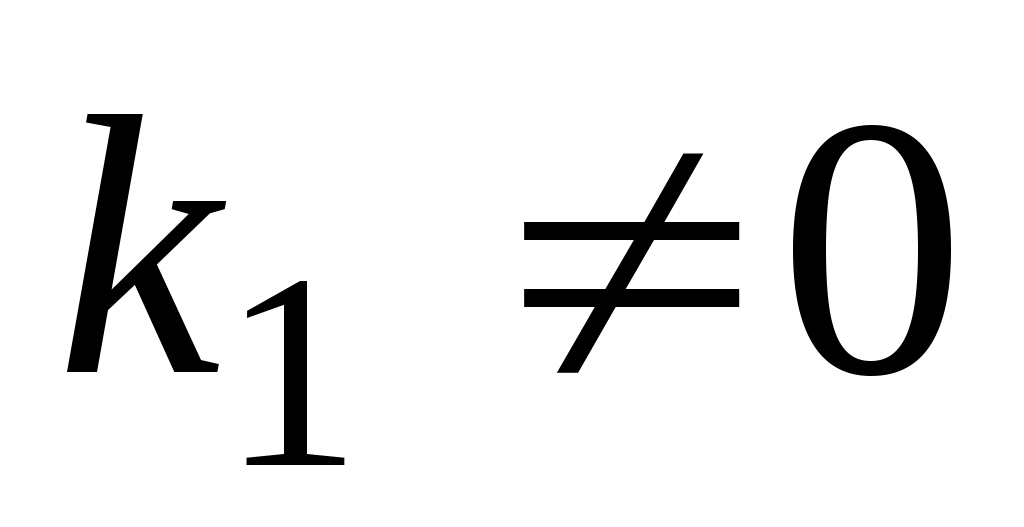 , , 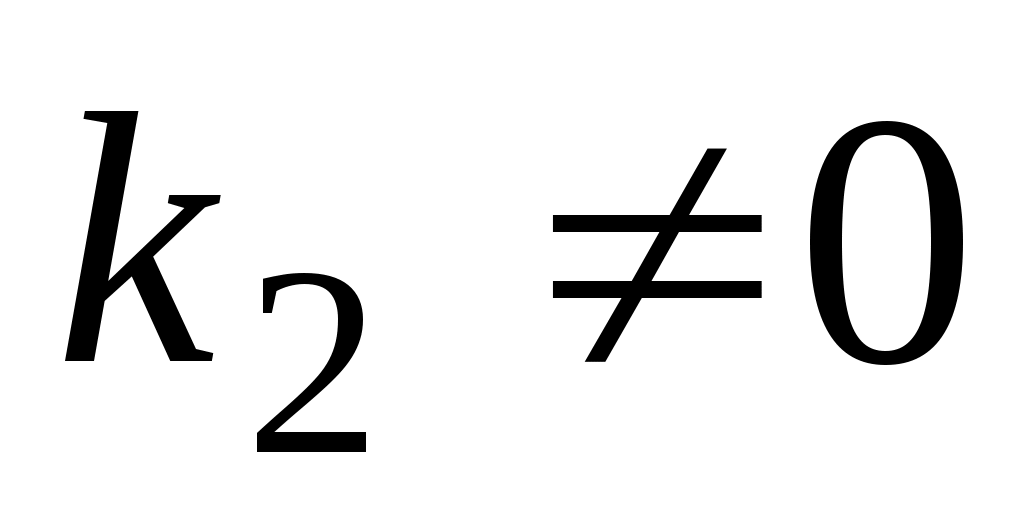 , , 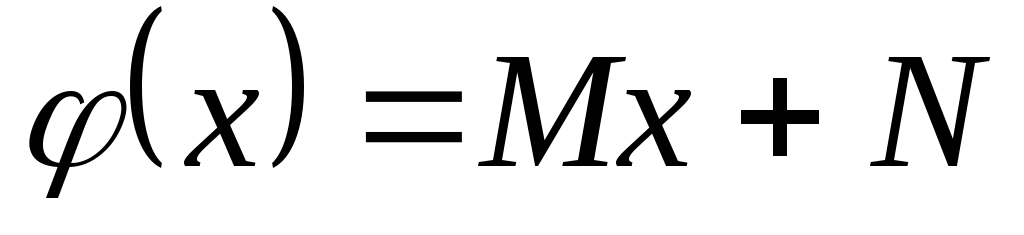 ; ;
б) 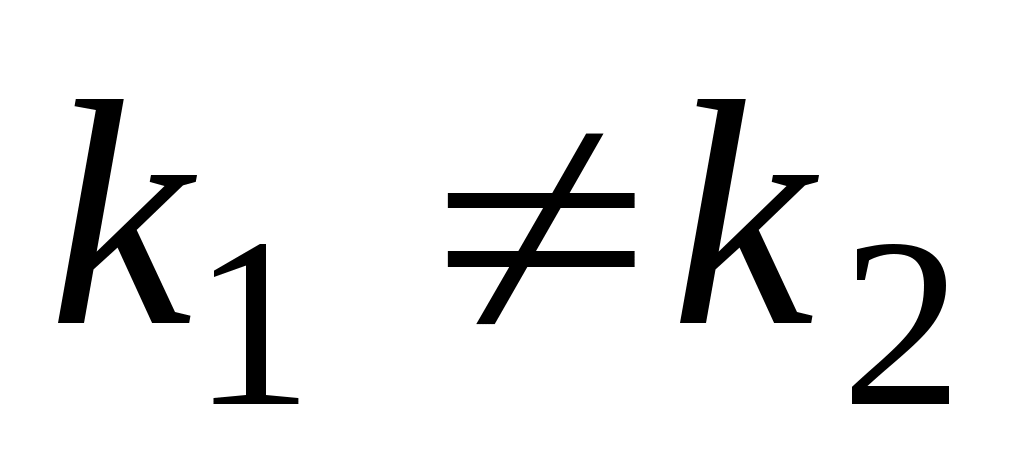 , , 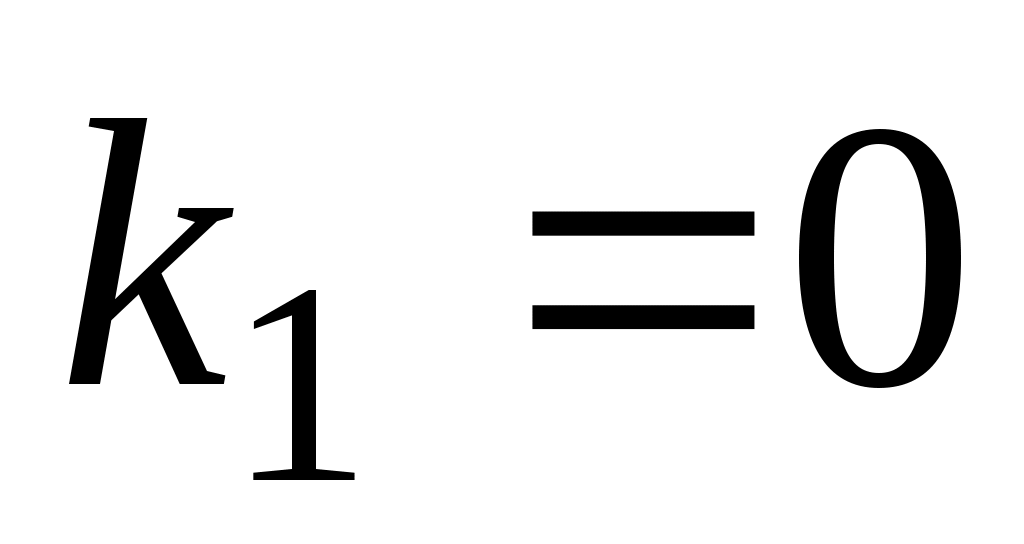 или или 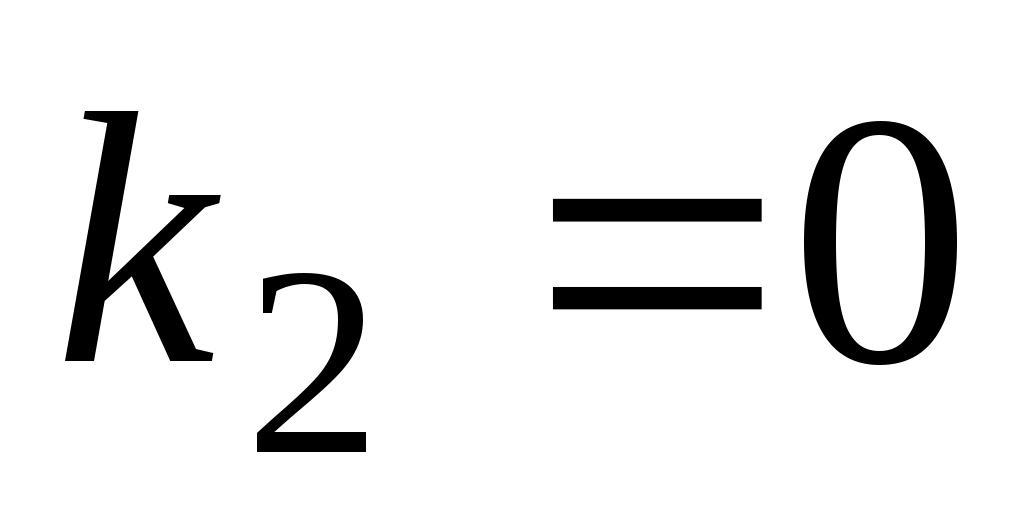  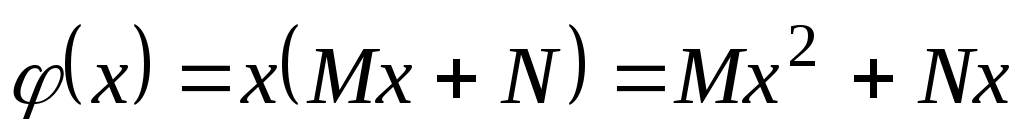 . .
2.1.2.2. 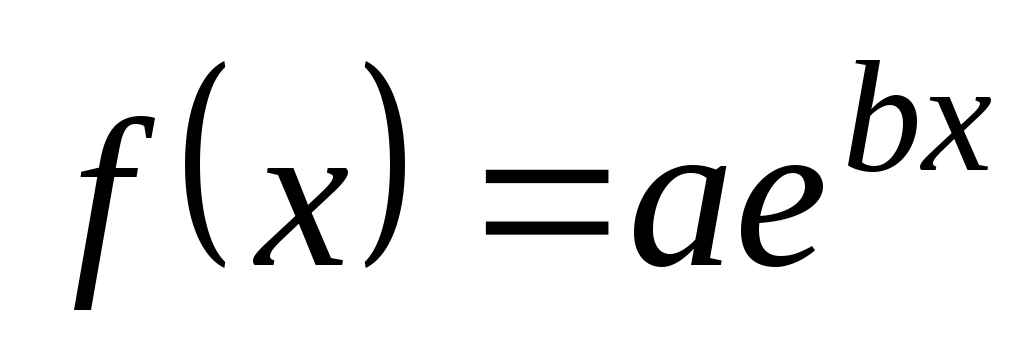
а) 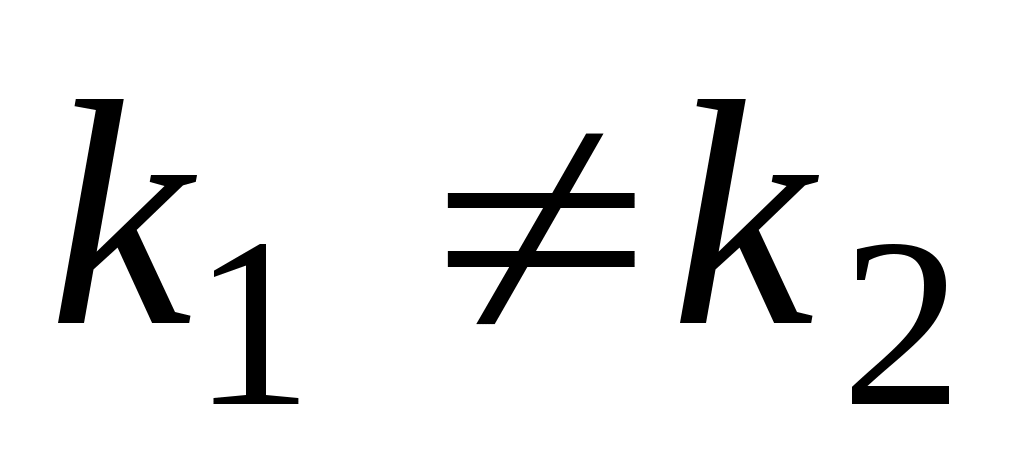 , , 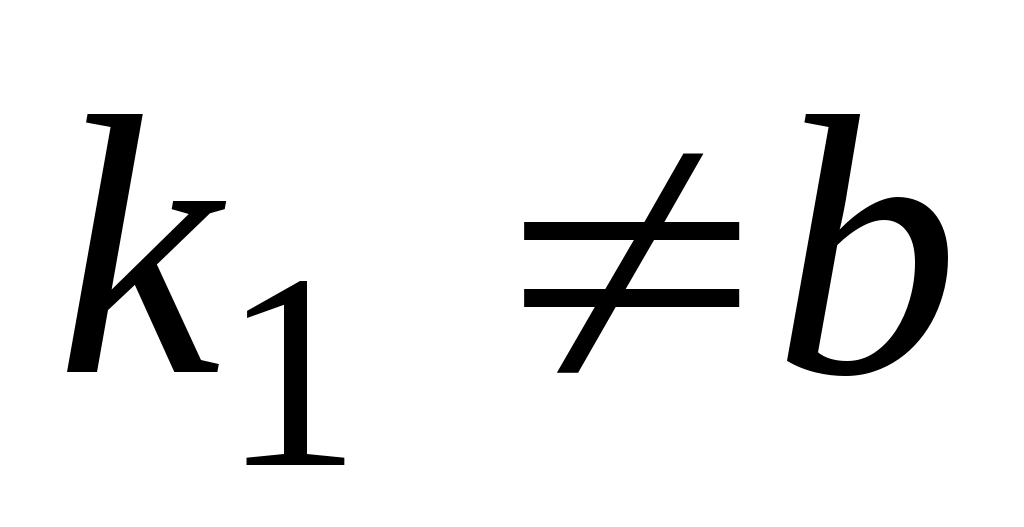 , , 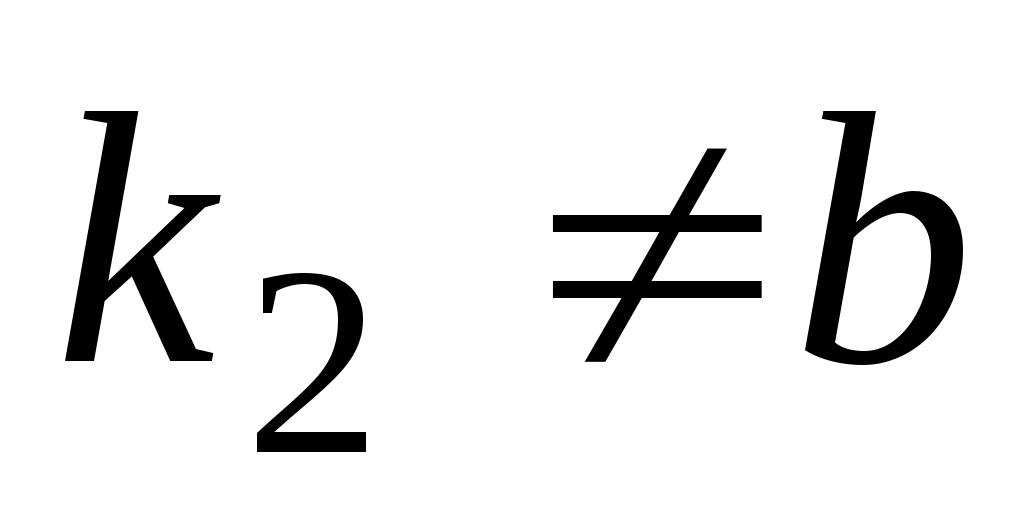  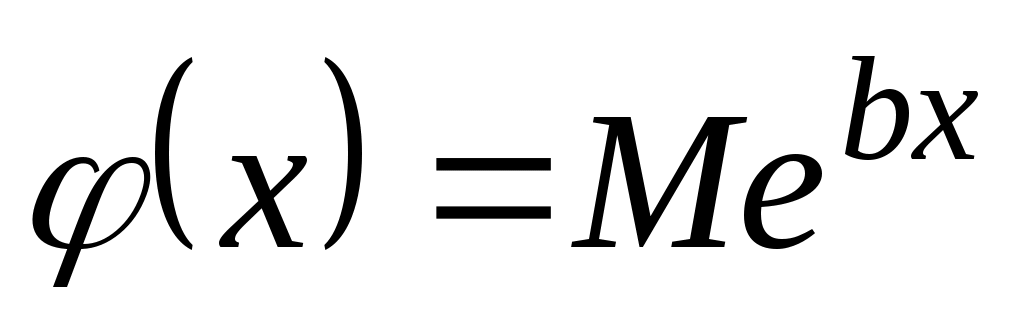 ; ;
б) 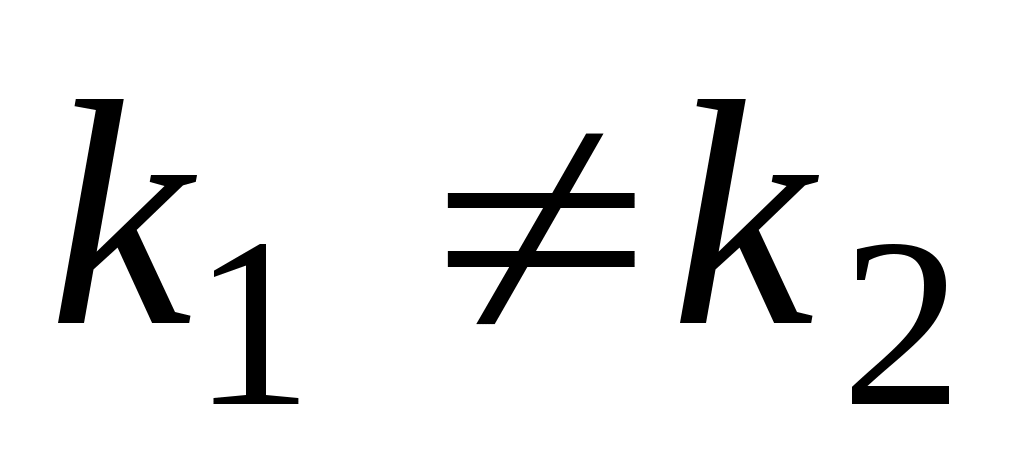 , , 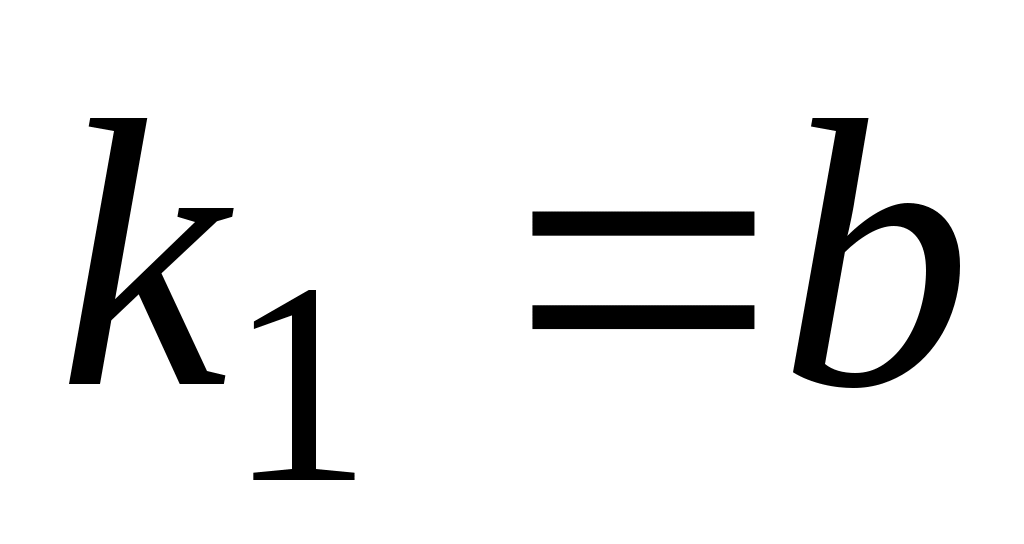 или или 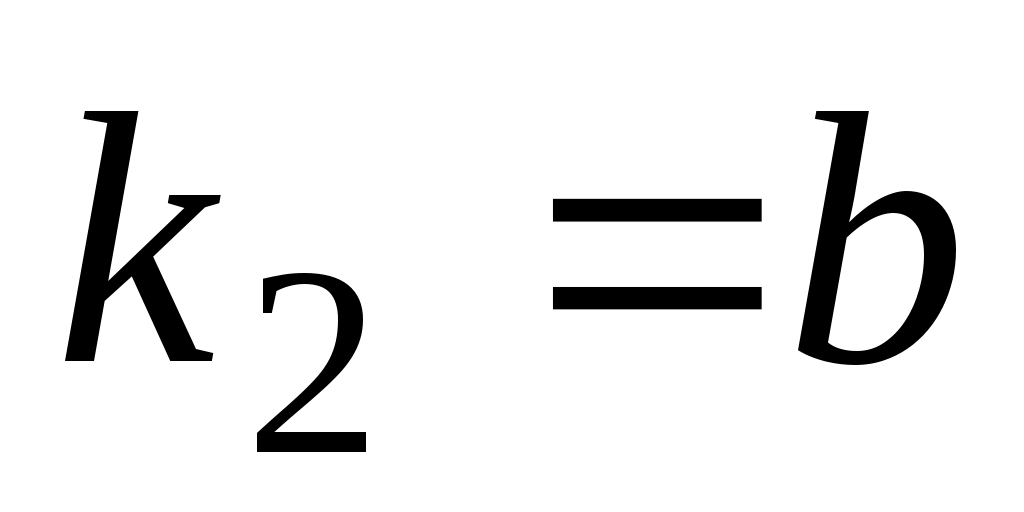  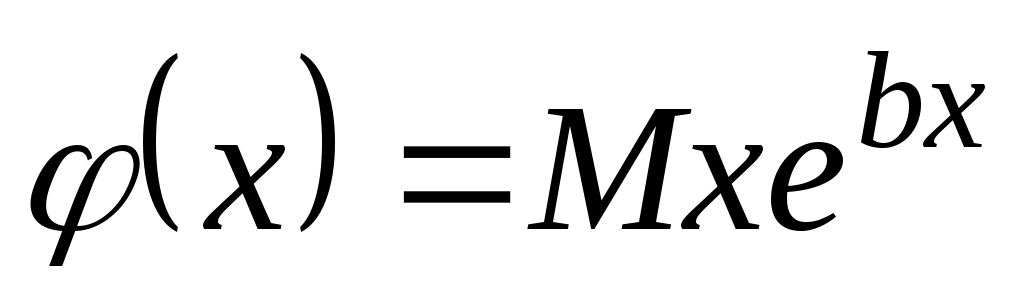 . .
в) 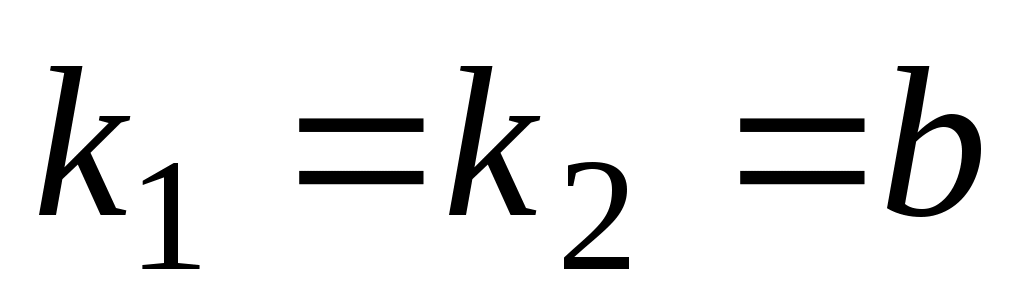  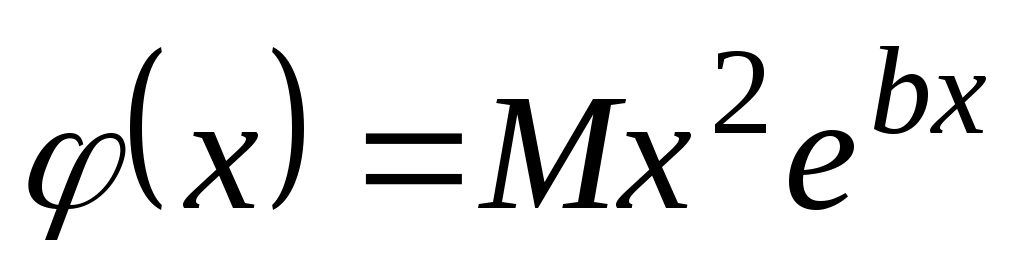 . .
2.1.2.3. 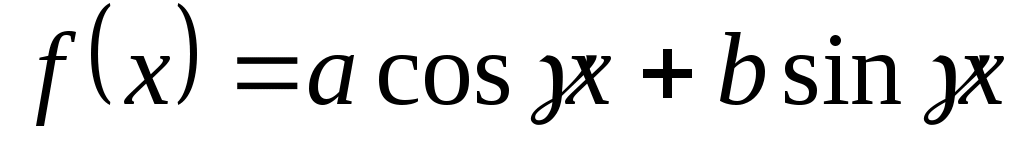 (а, (а, 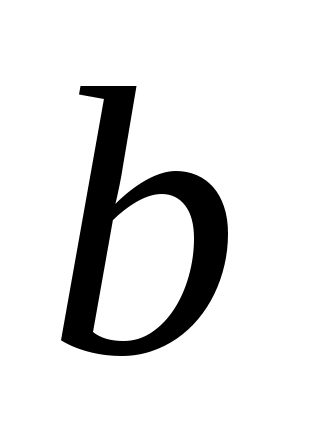 , , 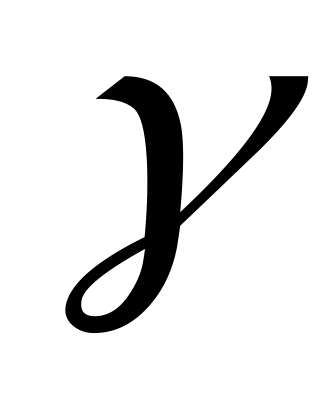 – данные числа, а или – данные числа, а или 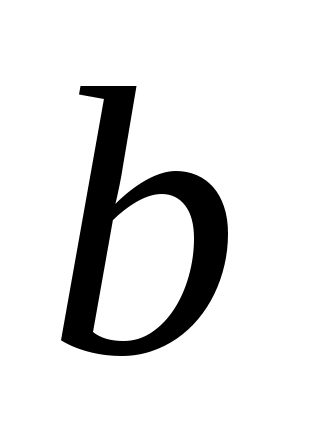 может быть равно 0). может быть равно 0).
а)  , , 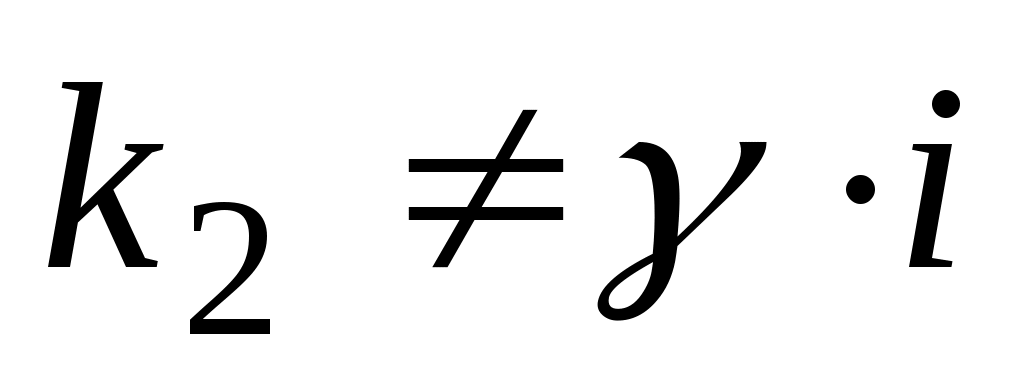 , ,  ; ;
б) 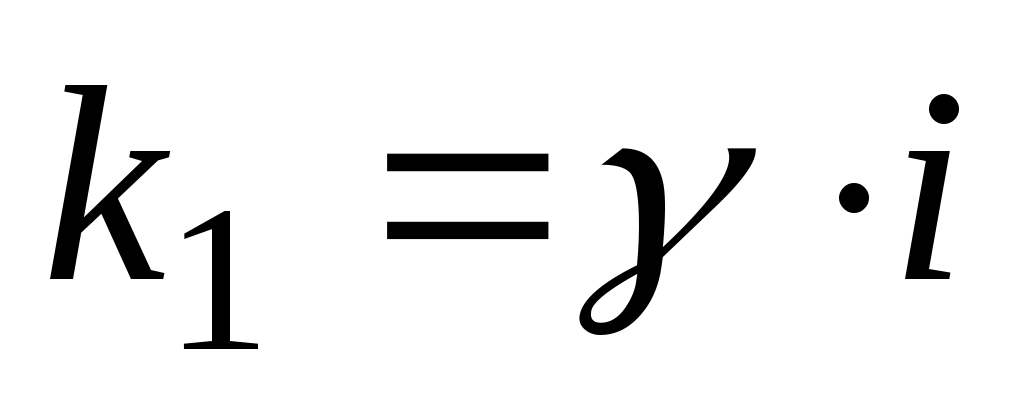 или или 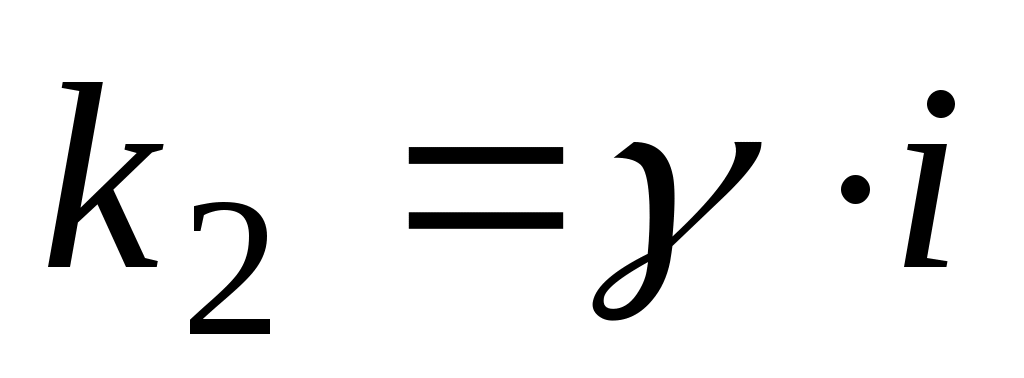  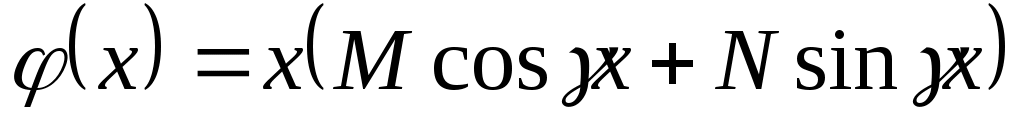 . .
Коэффициенты M и N находят методом неопределённых коэффициентов. Подставим 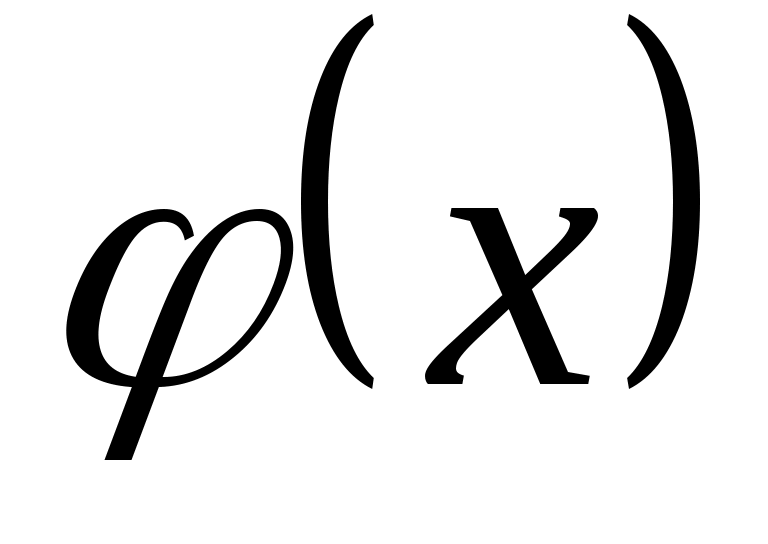 , , 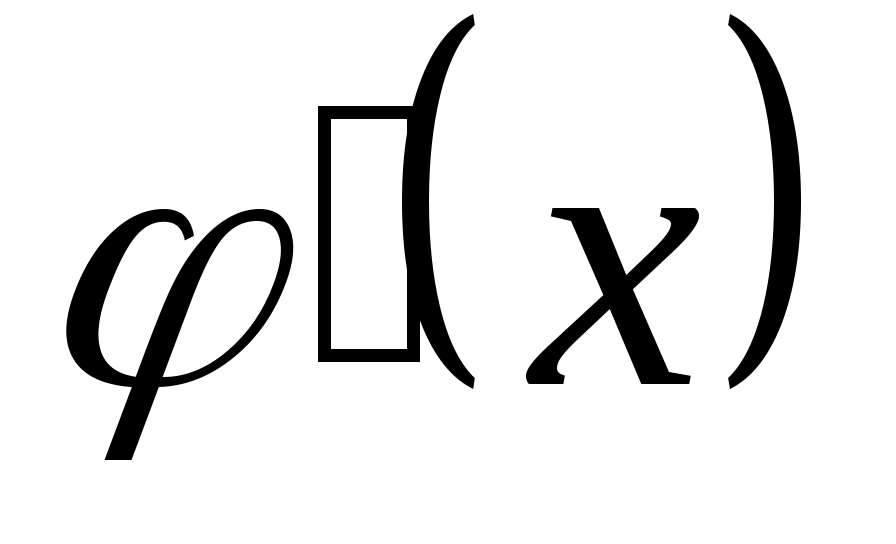 , , 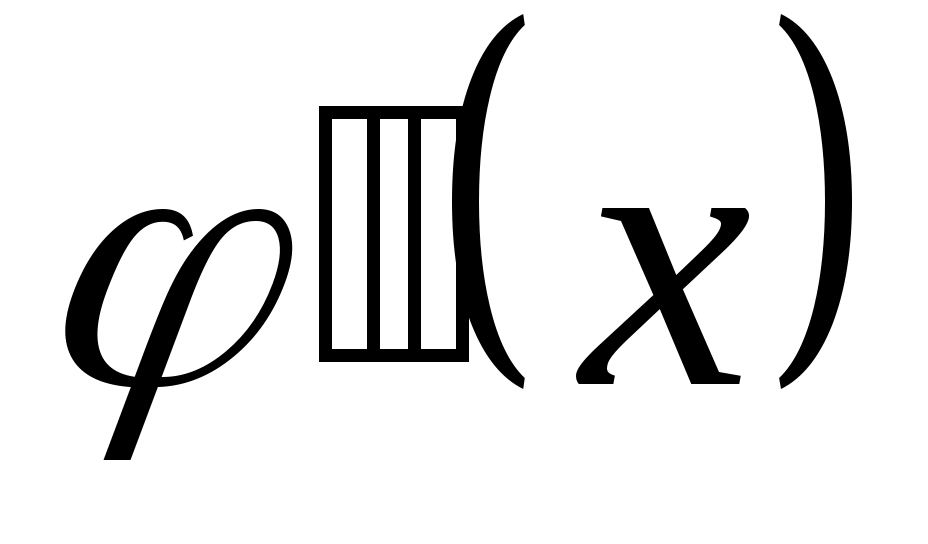 в уравнение 2.1. получим в уравнение 2.1. получим 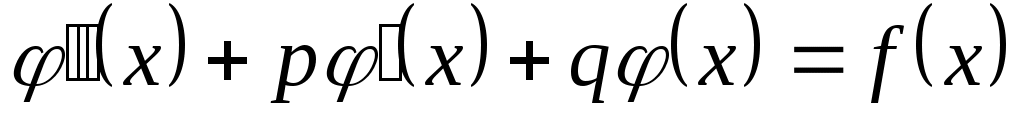 . Приравняем коэффициенты в левой и правой части при одинаковых степенях х, или при . Приравняем коэффициенты в левой и правой части при одинаковых степенях х, или при 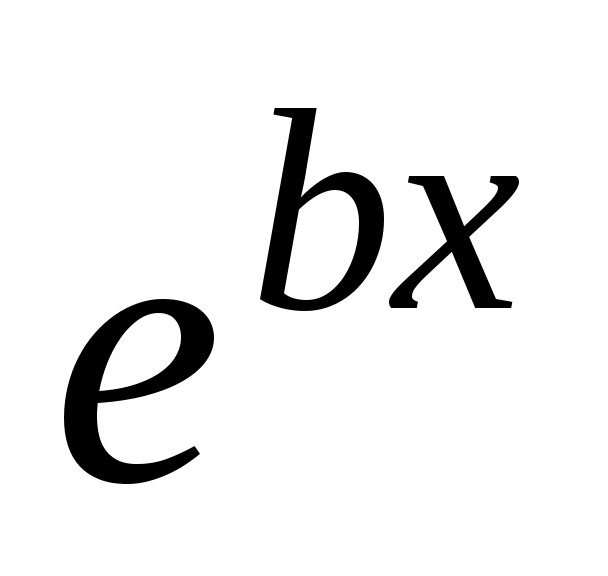 , или при , или при 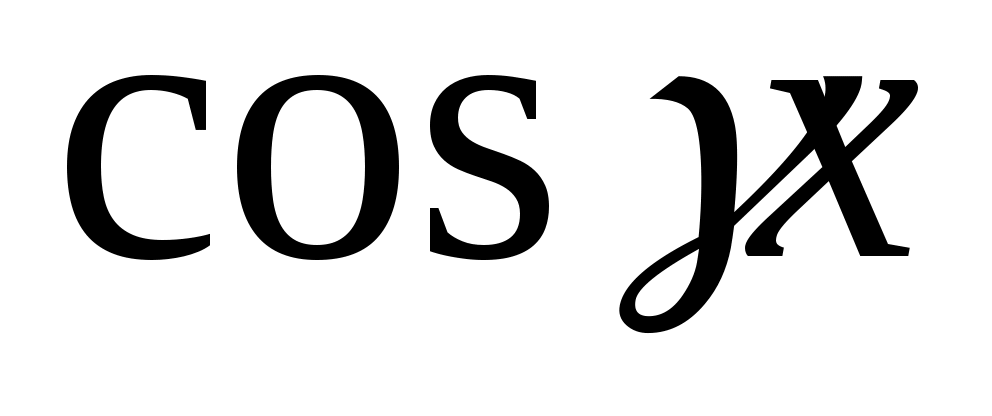 , или при , или при 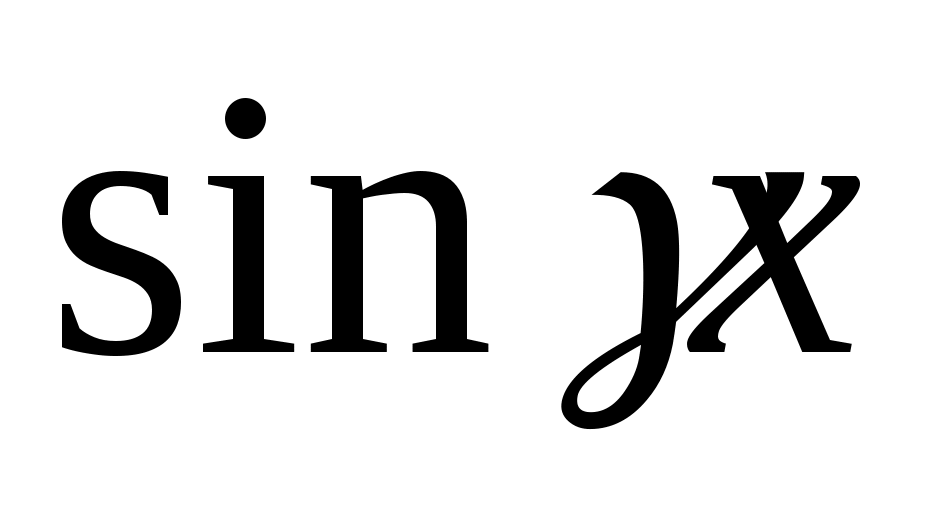 , или при , или при 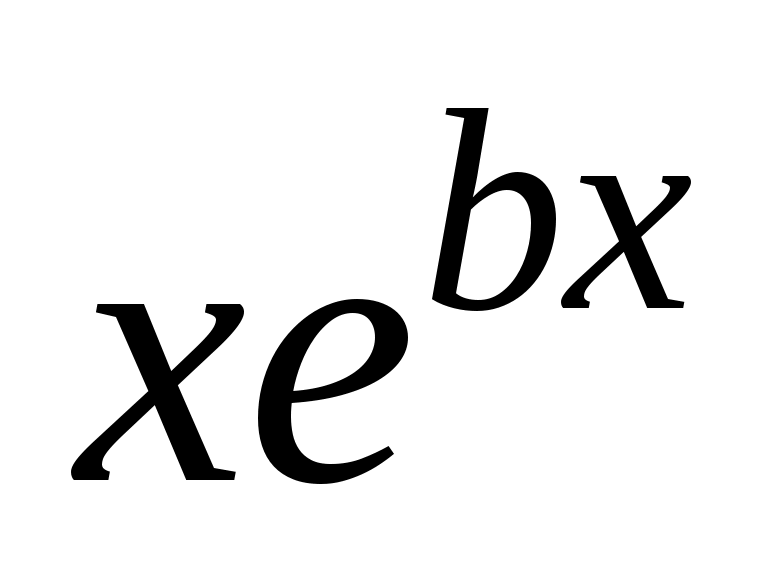 , или при , или при 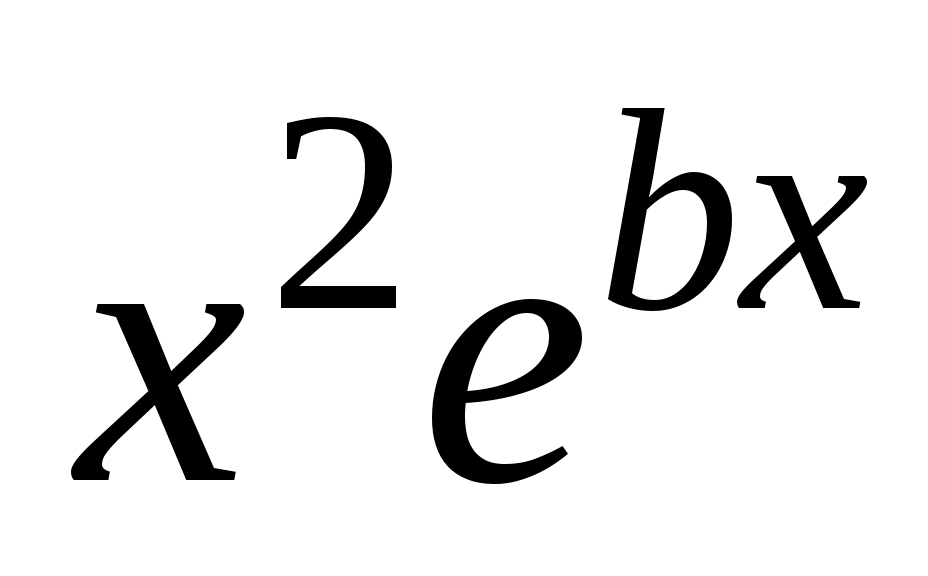 , или при , или при  и при и при 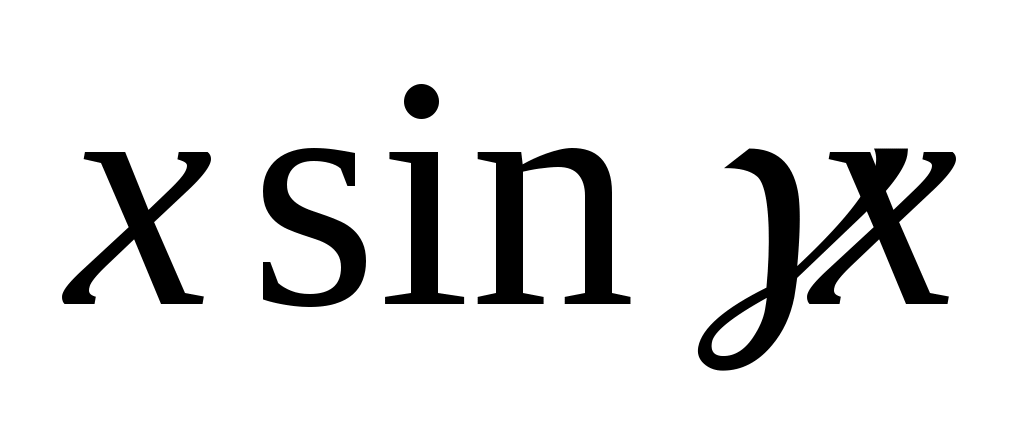 . .
2.1.3. Частное решение дифференциального уравнения при заданных начальных условиях 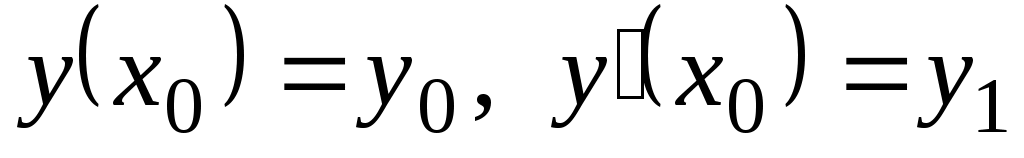 . Выпишем общее решение неоднородного уравнения: . Выпишем общее решение неоднородного уравнения: 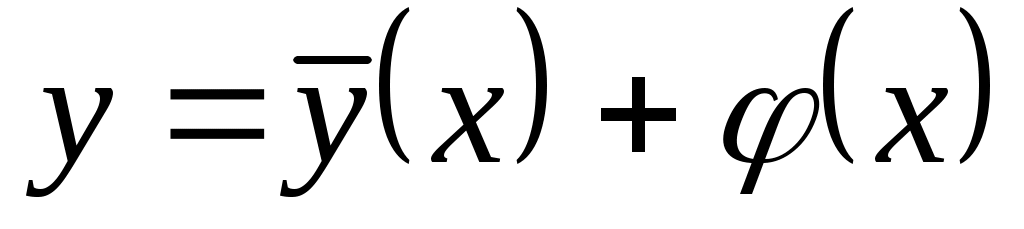 , найдем , найдем 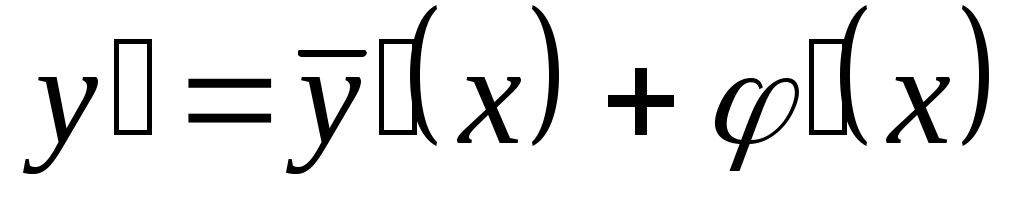 . Подставим начальные условия в выражение для . Подставим начальные условия в выражение для 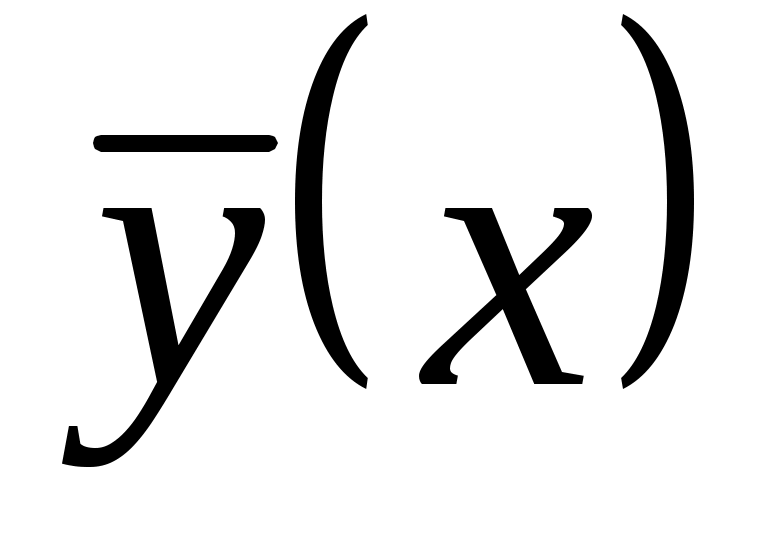 и и 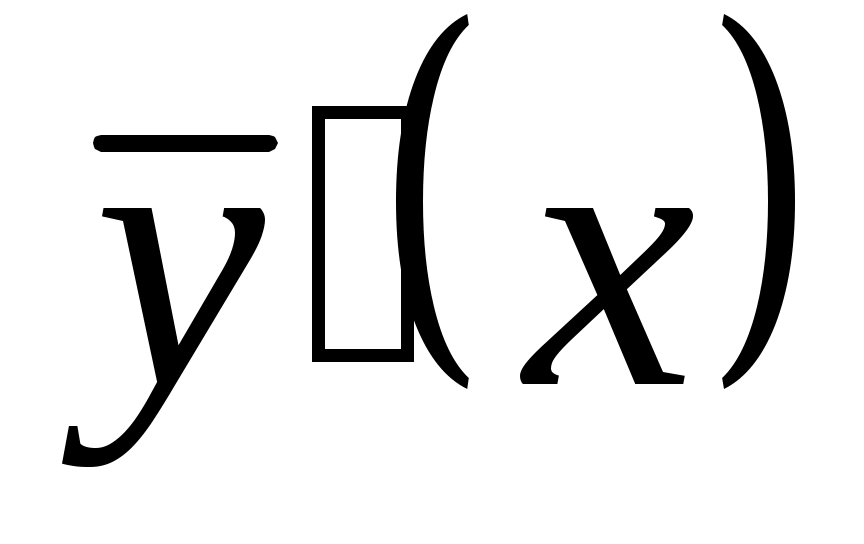 , получим систему двух уравнений относительно , получим систему двух уравнений относительно  и и 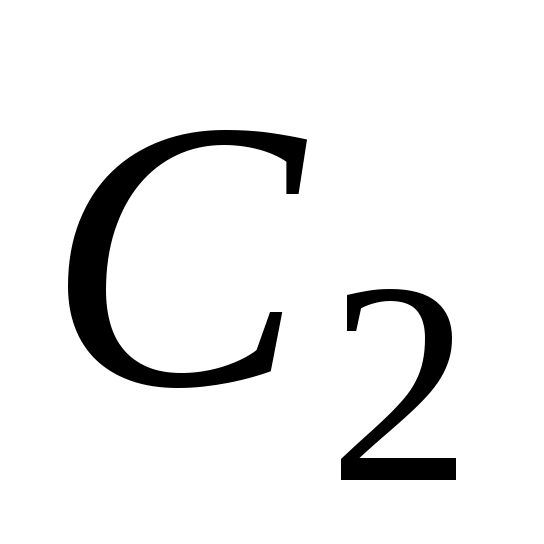 . Найдя . Найдя 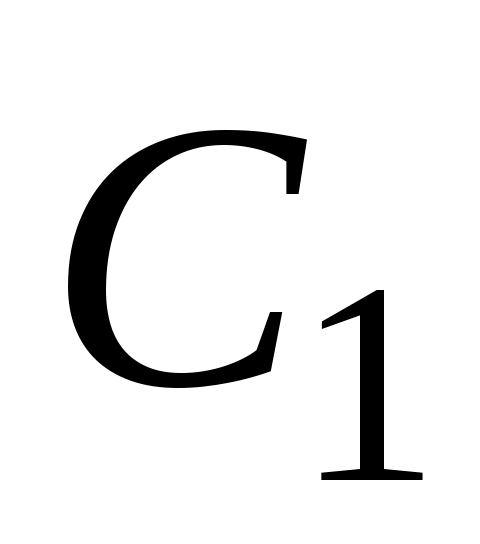 и и 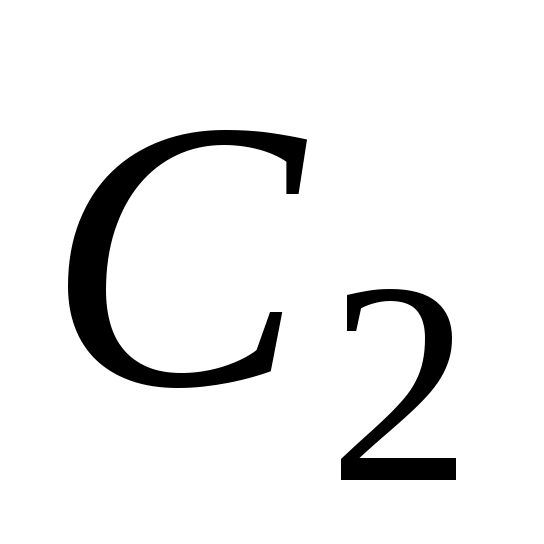 , подставим их значения в решение у. , подставим их значения в решение у.
|
|
|
 Скачать 1.36 Mb.
Скачать 1.36 Mb.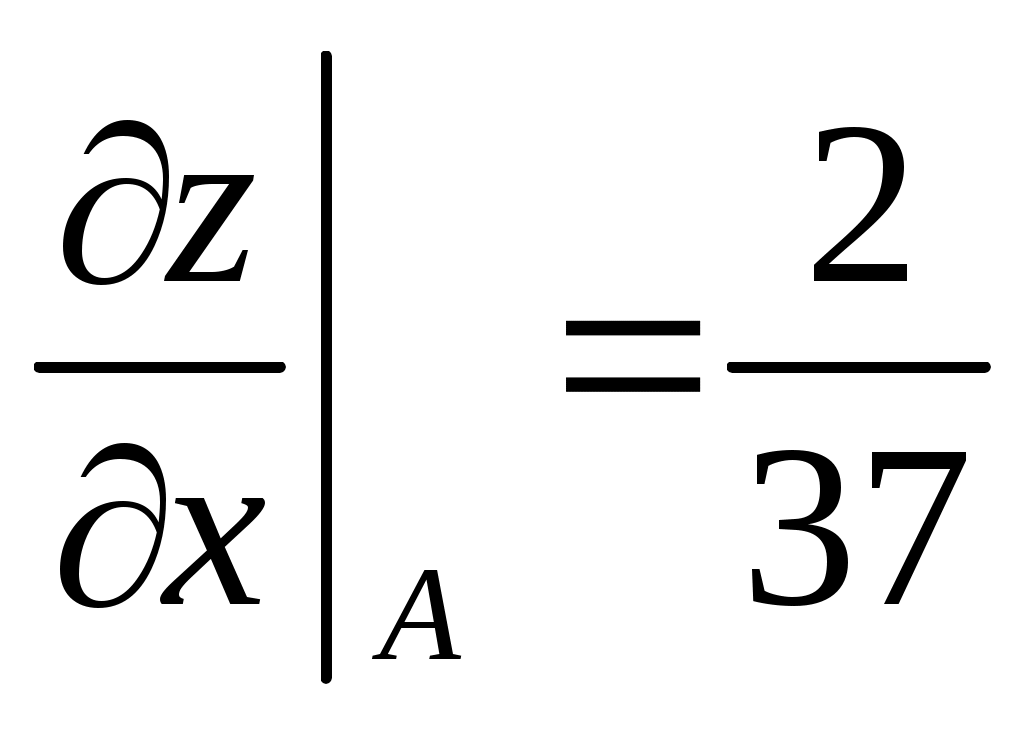 ;
; 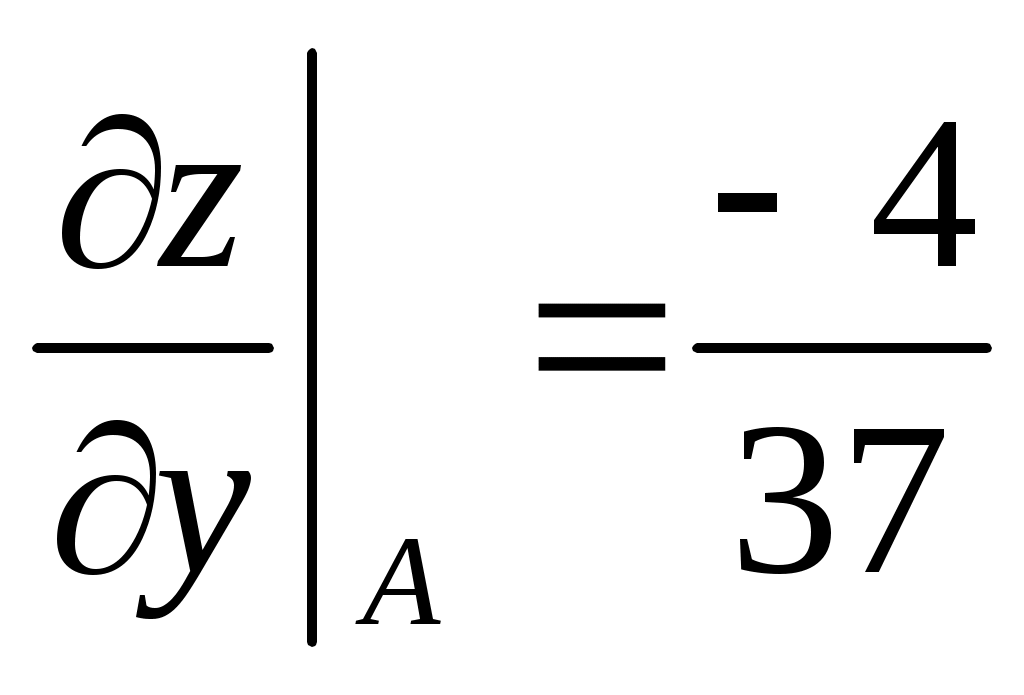 ;
;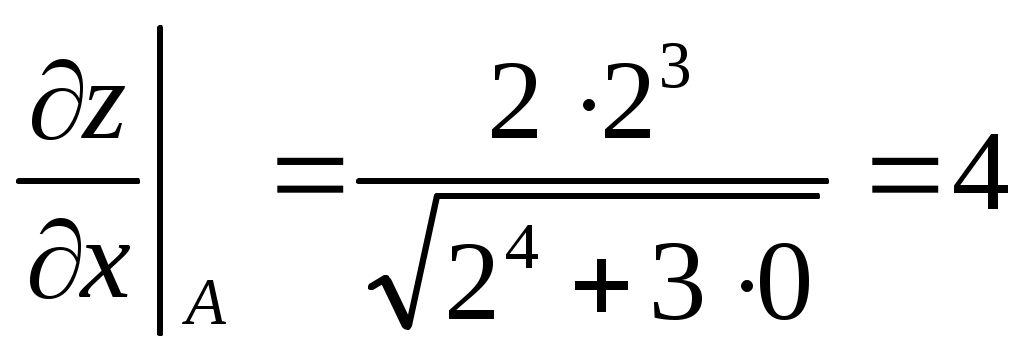 ;
;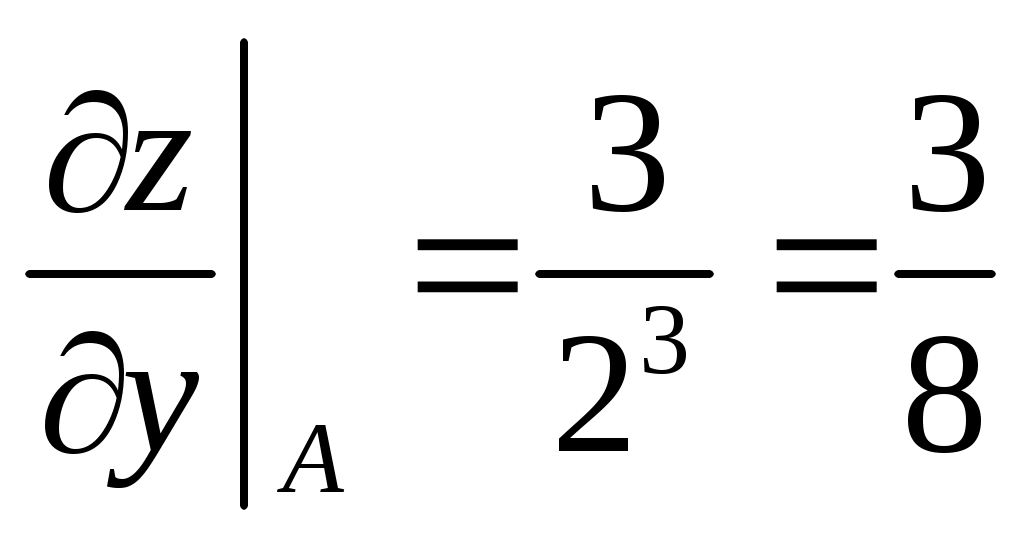 (использовалась формула
(использовалась формула 