математика краткая теория 2 курс. Дифференциальное исчисление функций нескольких переменных
 Скачать 1.36 Mb.
|
|
6. Пусть криволинейная трапеция, ограниченная прямыми линиями  ,  и частью графика кривой  , вращается вокруг оси  . Тогда объем полученного при этом тела вращения вычисляется по формуле . (5.14)Пример 1. Найти  .▲ Используя формулы (5.1), имеем  ▼Проверка.  Пример 2. Найти  .▲ Применяя (5.2), получим  . ▼Пример 3. Найти  .▲ Применяя формулу (5.3), имеем    . ▼Пример 4. Найти  .▲     . Перенося последний интеграл в левую часть равенства, получим  .Следовательно,  . ▼Пример 5. Найти  .▲ Рациональная подынтегральная дробь является правильной (см. методы интегрирования 4) и разлагается на простейшие дроби вида (5.4):  .Если привести дроби из данного разложения к общему знаменателю, то он совпадает со знаменателем исходной подынтегральной функции. Числители в левой и правой частях последнего равенства будут тождественно равными, т. е.  .Для нахождения неизвестного коэффициента A используем метод частных значений, т. е. подставим вместо переменной x ее частное значение, совпадающее с вещественным корнем знаменателя,  . Получим равенство  , откуда следует, что  .Для вычисления значений M, N используем метод неопределенных коэффициентов. Приравнивая коэффициенты при одинаковых степенях x в обеих частях полученного тождества, получаем систему уравнений   решение:  .Таким образом,    . ▼Пример 6. Найти  .▲   . ▼Пример 7. Вычислить несобственные интегралы или установить их расходимость: 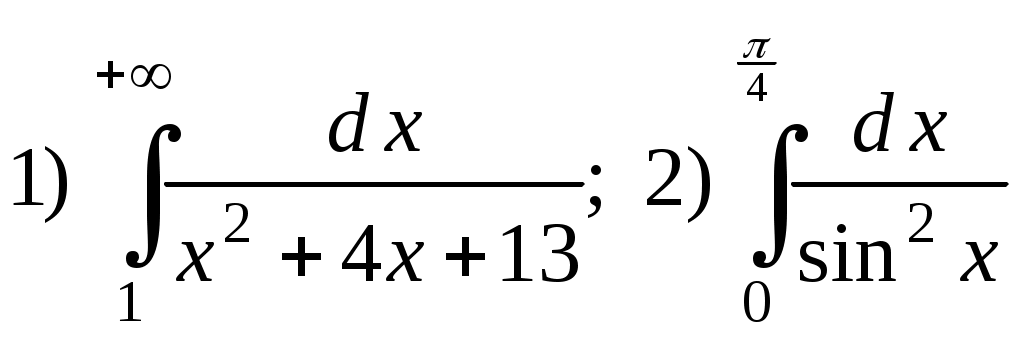 .▲ 1) Первый интеграл является несобственным интегралом с бесконечным верхним пределом интегрирования. Согласно определению (5.9), имеем   2) Второй интеграл является несобственным интегралом от неограниченной функции; функция 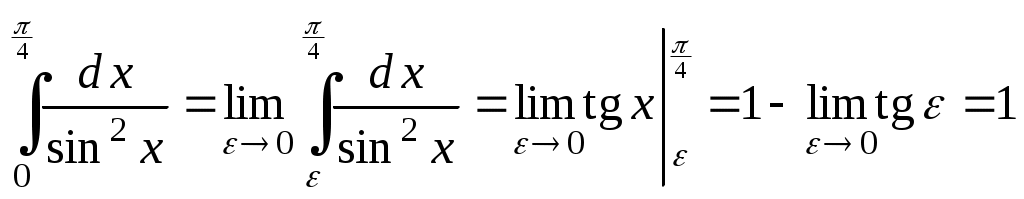 терпит бесконечный разрыв в нижнем пределе  . Согласно определению (5.10) получаем .Оба несобственных интеграла сходятся. ▼ Пример 8. Вычислить площадь фигуры, ограниченной линиями  и  .▲ Находим точки пересечения данных кривых (рис. 9): 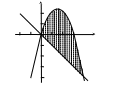  у  2–2 O 1 2 х –1 –4 Рис. 9 Следовательно, по формуле (5.8) имеем (см. рис. 8)   . ▼Пример 10. Вычислить объем тела, образованного вращением вокруг оси кривой  .▲ Объем полученного тела вращения найдем по формуле (5.14):  . ▼ЗАДАНИЯ Сдать 20.11.2020 до 15.00 №1. 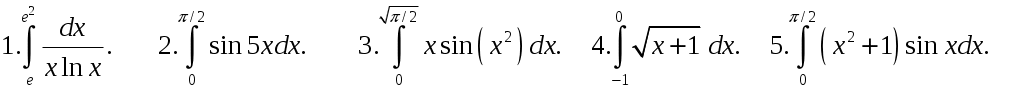 №2. 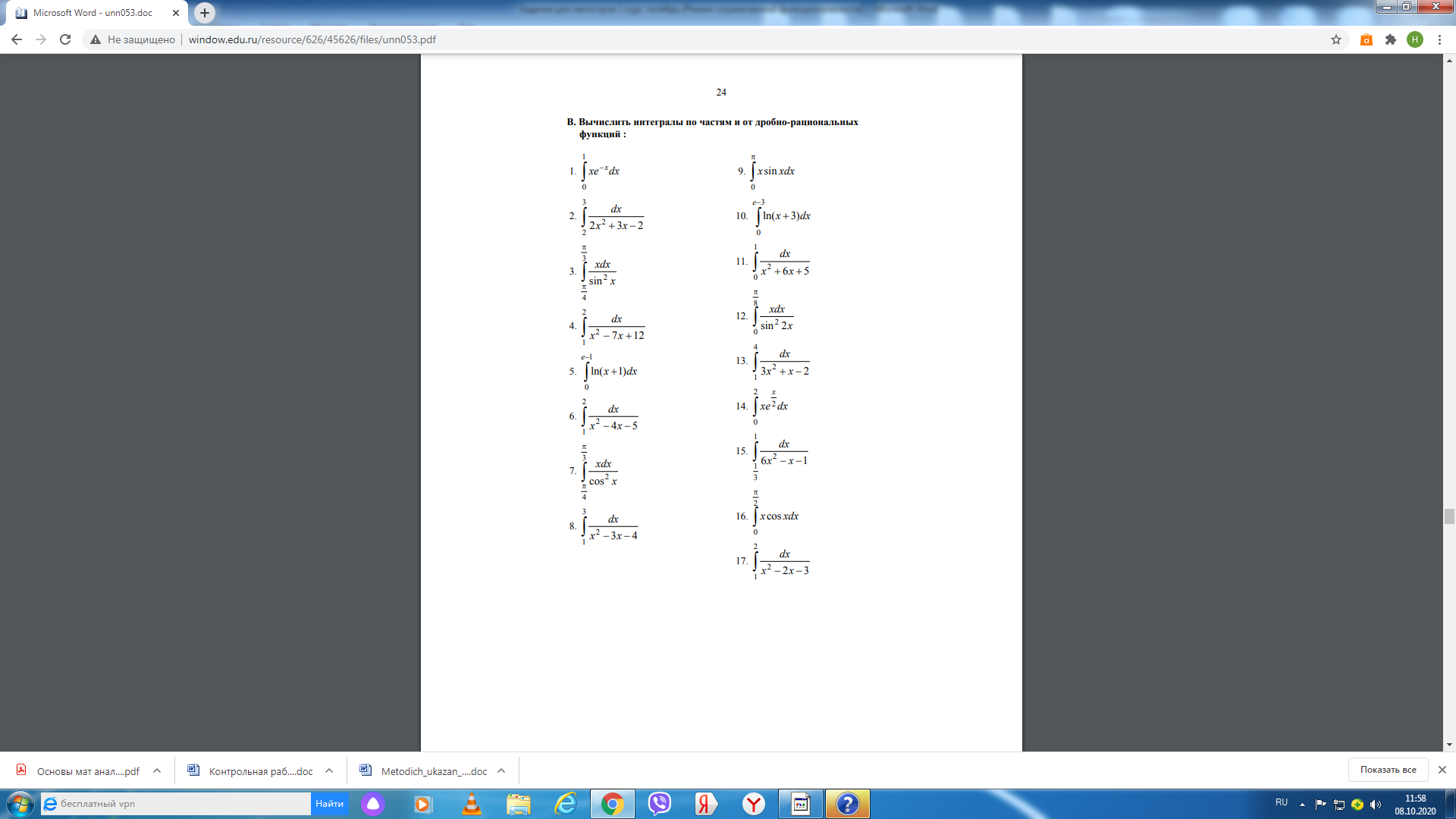 №3. 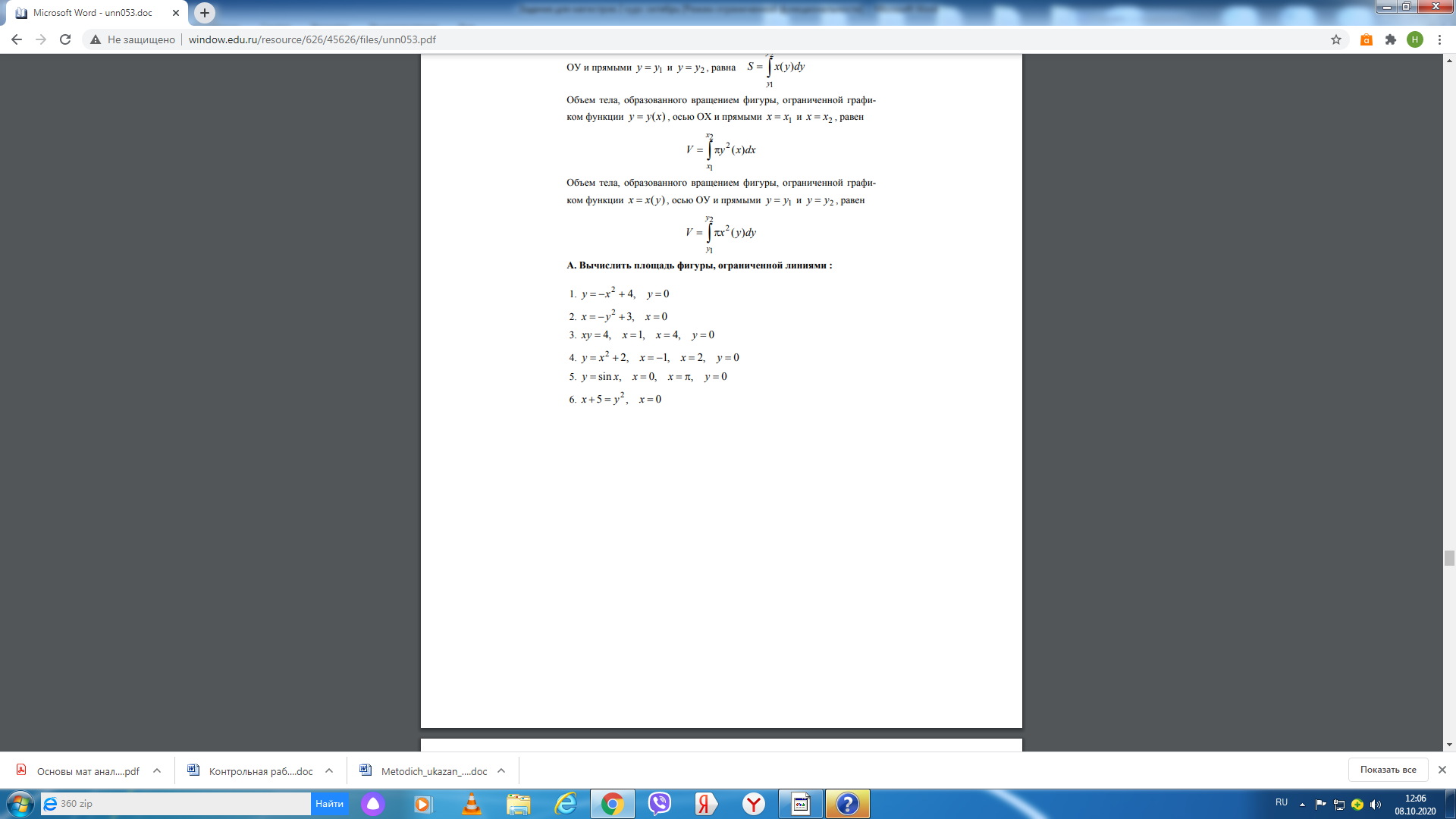 |