математика краткая теория 2 курс. Дифференциальное исчисление функций нескольких переменных
 Скачать 1.36 Mb. Скачать 1.36 Mb.
|
|
Примеры Найти общее решение дифференциального уравнения Это уравнение с разделяющимися переменными 1.1. а) Решение Найти общее решение дифференциального уравнения Это линейное уравнение I порядка 1.2. Замена Найти частное решение дифференциального уравнения Решение. а) Однородное уравнение б) Частное решение неоднородного уравнения (2.1.2) Ищем 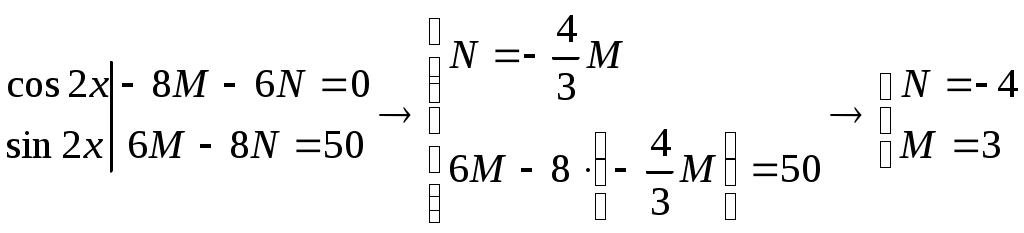 . Итак, . Итак, в) Общее решение: г) Найдём частное решение при начальных условиях (по 2.1.3): 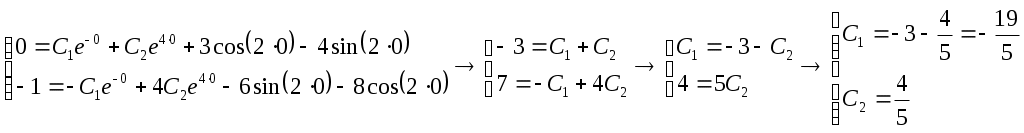 . Частное решение: при . Частное решение: при ЗАДАНИЯ (только четные №) Сдать 23.10.2020 до 15.00 Найти общее решение дифференциального уравнения I порядка. Найти частное решение дифференциального уравнения II порядка
Тема: «Теория вероятностей. Случайные величины» Краткая теория и методические указания. Случайные величины (СВ) Случайной величиной Х называется величина, которая случайно принимает какое-то значение из совокупности своих значений. Функция распределения 1.2.1 Вероятность того, что случайная величина Х примет значение в интервале Дискретные случайные величины (ДСВ). Значениями их являются только отдельные точки числовой оси. 1.3.1 Закон распределения ДСВ Х можно задать в виде ряда распределений
В первой строке таблицы указаны все значения х ДСВ Х, а во второй строке – вероятности 1.3.2 Функция распределения ДСВ Х выражается формулой 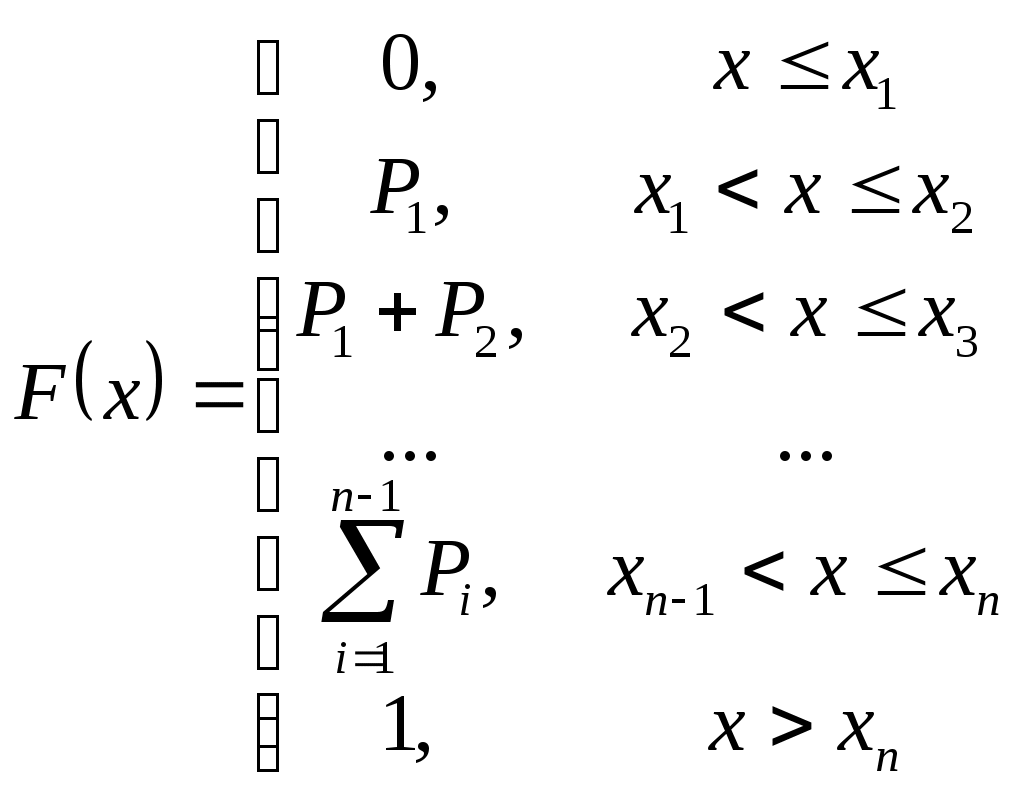 . .График Непрерывные случайные величины (НСВ). Значениями НСВ могут быть любые точки какого-то интервала на числовой оси. 1.4.1 Закон распределения НСВ задаётся функцией плотности распределения 1.4.2 Функция распределения НСВ вычисляется по формуле 1.4.3 Площадь под графиком 1.4.4 Вероятность того, что НСВ Х примет значения в интервале 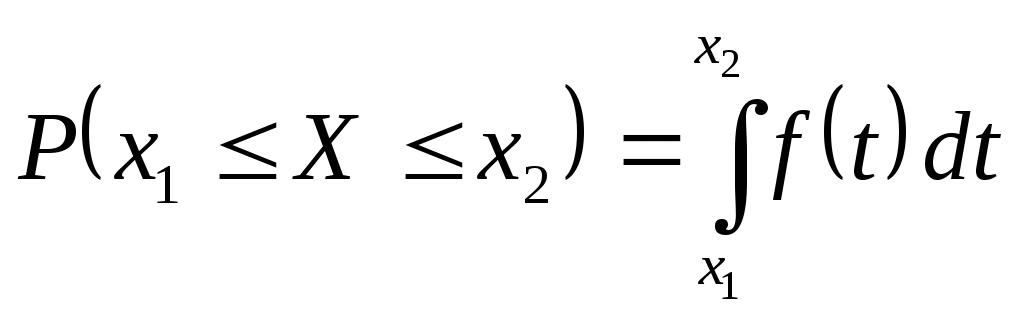 . При . При Числовые характеристики случайных величин Математическое ожидание Для ДСВ Дисперсия Для ДСВ: Среднее квадратическое отклонение Нормальное распределение Обозначается Функция плотности вероятностей 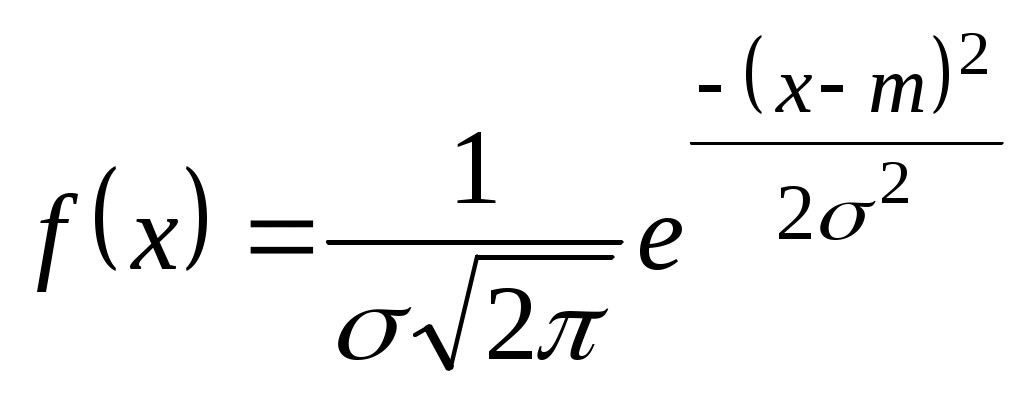 . . Математическое ожидание Функция распределения 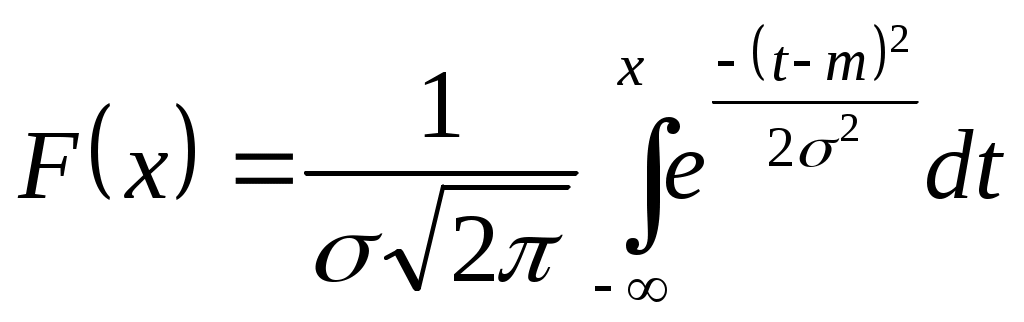 . .Нормированное нормальное распределение Вероятность того, что Примеры решения заданий Задание 1. Дискретная случайная величина Х задана рядом распределения.
Найти функцию распределения Решение: Найдём функцию распределения 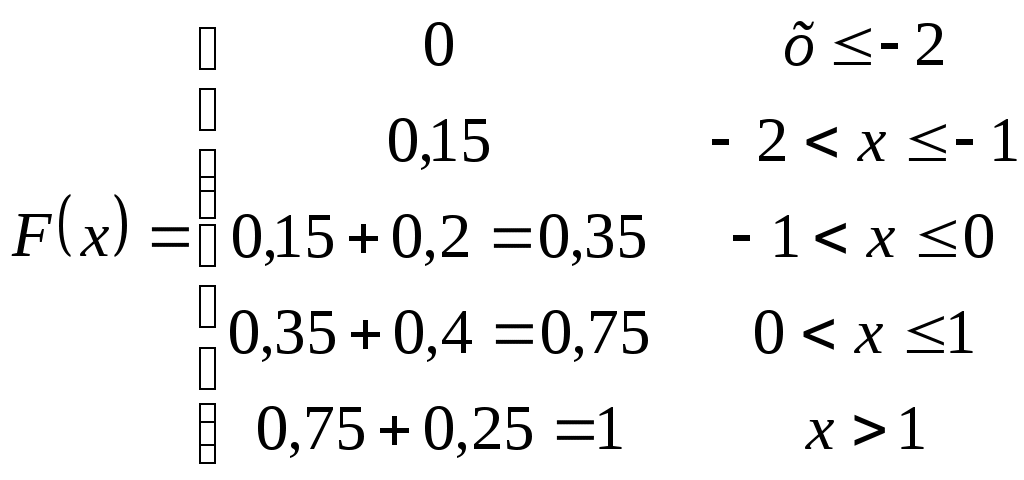 по (2.2.1) М График  атематическое ожидание по (3.1) . атематическое ожидание по (3.1) .    1   ; ; Д 0,5 исперсия по (3.2)       x . С 1 -1 -2 реднее квадратическое отклонение (по 3.3) Задание 2. Непрерывная случайная величина Х задана функцией плотности вероятностей. 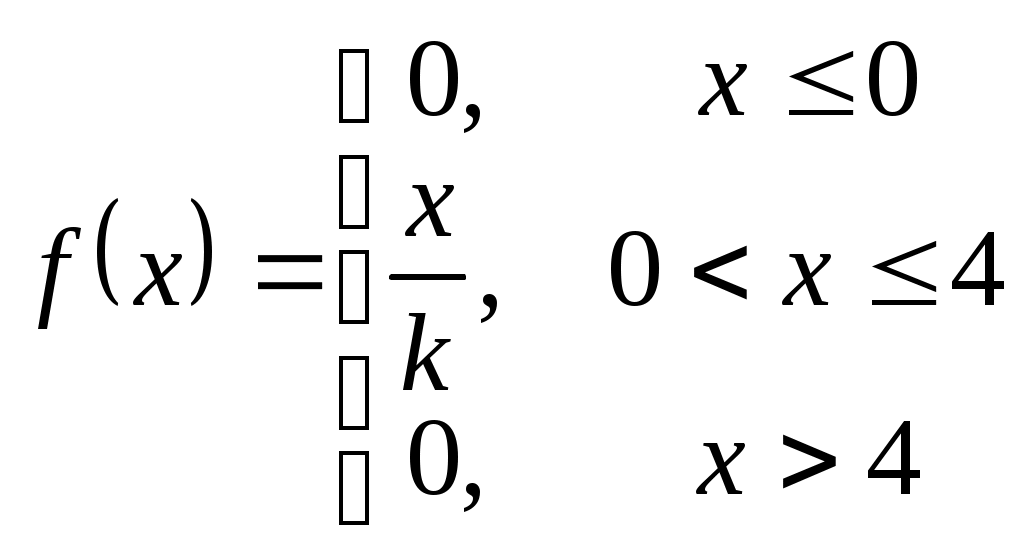 . Найти число k, функцию распределения . Найти число k, функцию распределения Решение: Найдем число 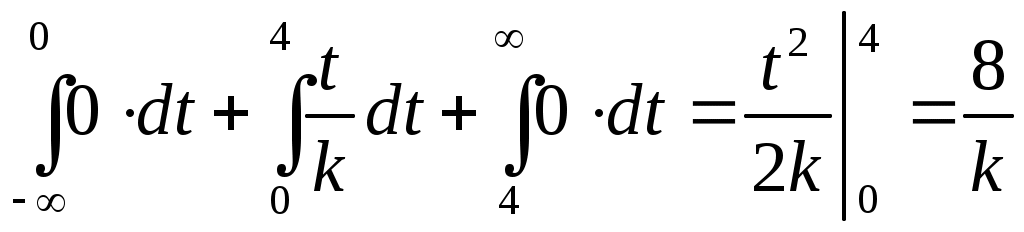 ; ; 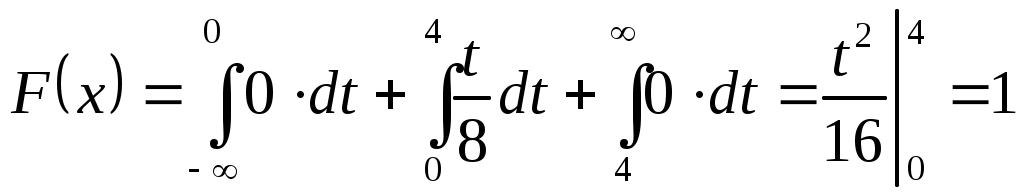 . .Г 1 4 х  рафики рафики            х 4   Математическое ожидание по (3.1) 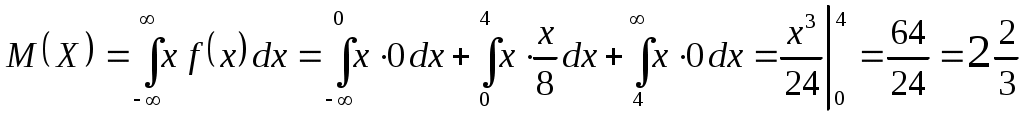 . . 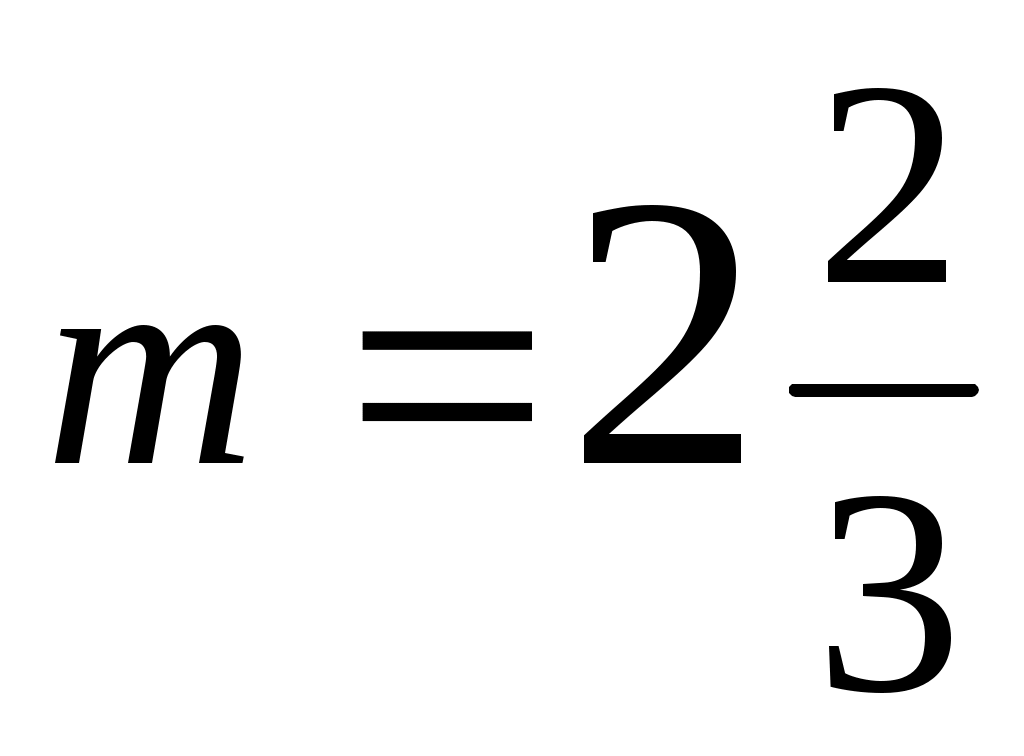 . .Дисперсия по (3.2) 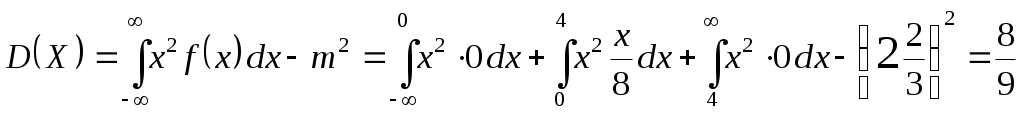 . .Задание 3. Дана нормальная случайная величина Решение: Вероятность попадания случайной величины 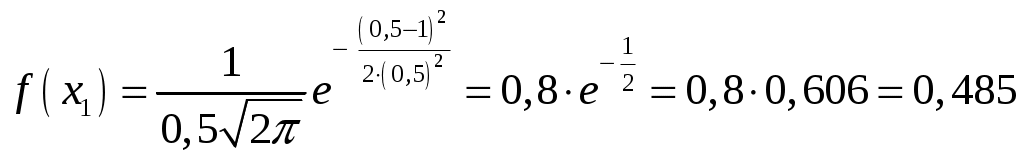 . . 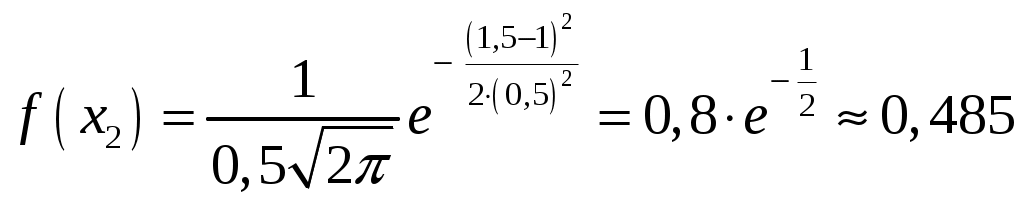 . .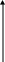 f(x) f(x)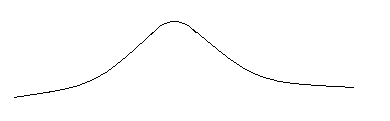 1       0,5 1 1,5 ЗАДАНИЯ (Каждая выбирает свой вариант по номеру в журнальном списке) Сдать 06.11.2020 до 15.00 Задание 1. Дискретная случайная величина Х задана рядом распределения
Найти функцию распределения Задание 2. Непрерывная случайная величина Х задана функцией плотности вероятностей 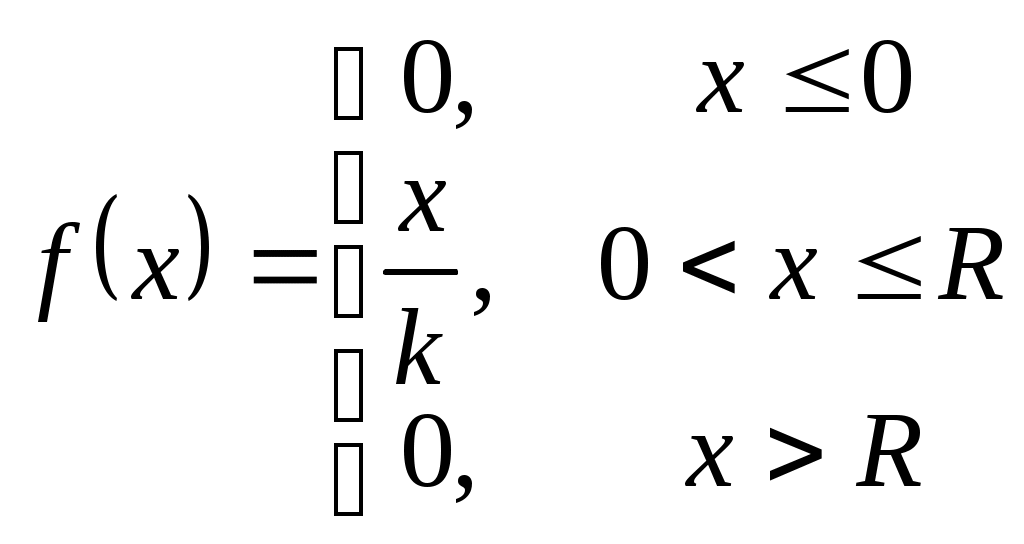 . Найти число k, функцию распределения . Найти число k, функцию распределения Задание 3. Дана нормальная случайная величина Варианты значений параметров контрольных заданий
Тема: «Неопределенный интеграл. Определенный интеграл» Основные теоретические сведения |
