математика краткая теория 2 курс. Дифференциальное исчисление функций нескольких переменных
 Скачать 1.36 Mb.
|
|
1. Определение первообразной функции (первообразной) и неопределенного интеграла. Пусть на интервале  задана функция  .Функция  называется первообразной для функции  на промежутке , если  .Теорема 1. Если  − две любые первообразные для функции на , то  .Следствие. Если − одна из первообразных для функции на , то любая другая первообразная  для функции на промежутке имеет вид  , где C − некоторая постоянная.Совокупность всех первообразных для функции на промежутке  называется неопределенным интегралом от функции на промежутке и обозначается  .В силу следствия из теоремы 1  ,где − одна из первообразных для , C − некоторая постоянная.2. Основные свойства неопределенного интеграла 1.  .2.  .3. Линейность интеграла. Если существуют первообразные функции  и  , а  − любые вещественные числа, то существует первообразная функция для функции  , причем .3. При интегрировании наиболее часто используется следующие методы. 1. Если  , то ,(5.1)  где a и b некоторые постоянные. 2. Простейшие приемы интегрирования, основанные на алгебраических преобразованиях подынтегральных функций. 3. Подведение под знак дифференциала  , (5.2)так как  .4. Формула интегрирования по частям:  . (5.3)Обычно выражение  выбирается так, чтобы его интегрирование не вызывало особых трудностей. За u, как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемых по частям, относятся, в частности, функции вида  : ,где  многочлен от x.Указания 1. Правило выбора частей: Если тригонометрическая или показательная функция, то следует положить  .Если логарифмическая или обратная тригонометрическая функция, то  .2. Интегрирование по частям можно применять несколько раз подряд. 3. Интегрирование по частям  и некоторых других интегралов можно привести к линейному уравнению относительно этих интегралов после двукратного применения формулы (5.3).5. Интегрирование рациональных дробей, т. е. отношений двух много членов  (соответственно m-й и n-й степени):  , сводится к интегрированию правильных дробей. Если  , то R(x) называется правильной дробью, если  неправильной дробью.Всякую неправильную дробь путем деления числителя на знаменатель можно представить в виде суммы некоторого многочлена и правильной дроби:  , где  многочлены;  правильная дробь  .Например,  неправильная дробь. Разделив ее числитель на знаменатель (по правилу деления многочленов «уголком», см. пример 1 ”Дифференциальное исчисление“), получим  .Интегрирование правильных дробей сводится к разложению подынтегральной функции  на простейшие, всегда интегрируемые дроби, вида , (5.4)где  постоянные числа; k целое положительное число, а трехчлен  не имеет вещественных корней.6. Интегрирование методом замены переменной (способ подстановки) является одним из эффективных приемов интегрирования. Его сущность состоит в переходе от переменной x к новой переменной  .При выборе подстановки оправдан был бы выбор по принципу “что хуже, сложнее − принять за новую переменную t”. Два способа замены переменной Переменную интегрирования в неопределенном интеграле можно заменить любой непрерывной функцией:  . (5.5)Формула (5.5) определяет собой два способа замены переменной. При чтении формулы слева направо получается способ I:  . Если  будет проще, чем интеграл , то эта замена переменной целесообразна. При чтении справа налево получается способ II: .Если последний интеграл проще первого, то замена переменной целесообразна Наиболее целесообразная для данного интеграла замена переменной, т. е. выбор функции  , не всегда очевидна. Однако для некоторых часто встречающихся классов функций можно указать такие стандартные подстановки, как ; ,где R символ рациональной функции. 2. Вычисление определенного интеграла. Определенный интеграл вычисляется по формуле Ньютона-Лейбница:  , (5.6)если  и первообразная функция  непрерывна на отрезке  .Определенный интеграл численно равен площади криволинейной трапеции, ограниченной прямыми линиями  и частью графика функции  , взятой со знаком плюс, если  , и со знаком минус, если  .Замена переменной в определенном интеграле осуществляется по тем же правилам, что и в неопределенном интеграле, только нет обратного перехода к исходной переменной, и есть новая операция − замена пределов интегрирования (новые пределы интегрирования вычисляются по старым пределам через замену). Самое главное при замене переменной не забывать заменять пределы интегрирования. Интегрирование по частям определенного интеграла. Для интегралов вида 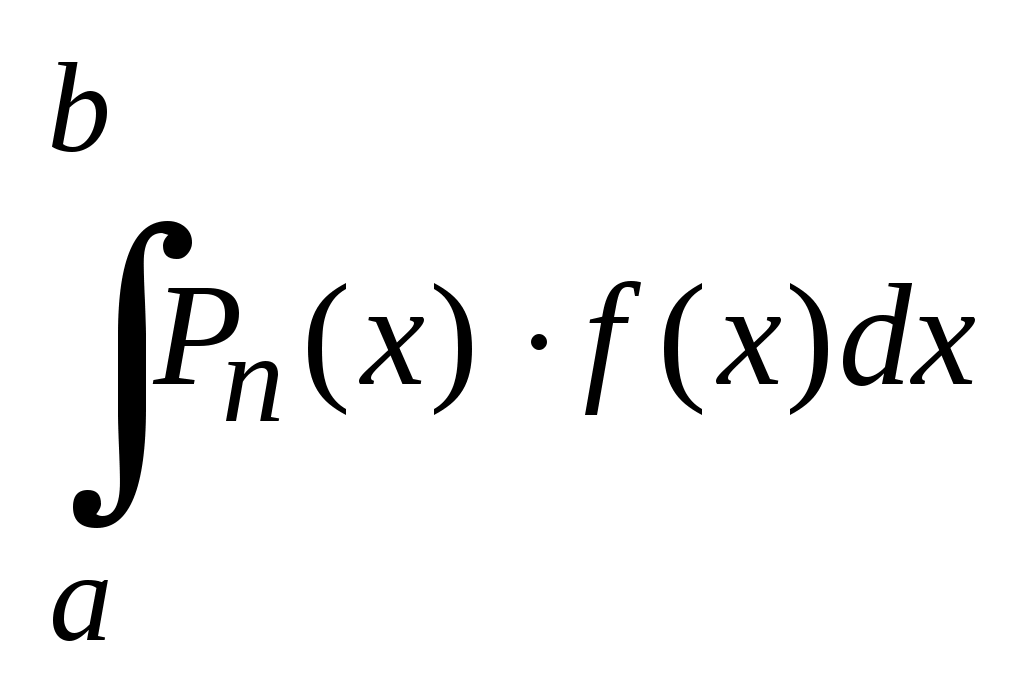 , где  − многочлен, а − основная элементарная функция, применяется формула интегрирования по частям: . (5.7)Отличие от аналогичной формулы для неопределенного интеграла только в расстановке пределов. Вычисление определенных интегралов с симметричными пределами. Если, пределы интегрирования симметричны относительно нуля, то 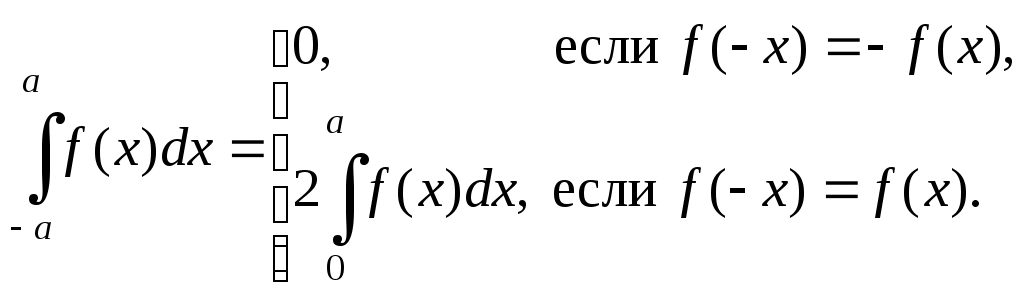 (5.8)5. Если интервал интегрирования 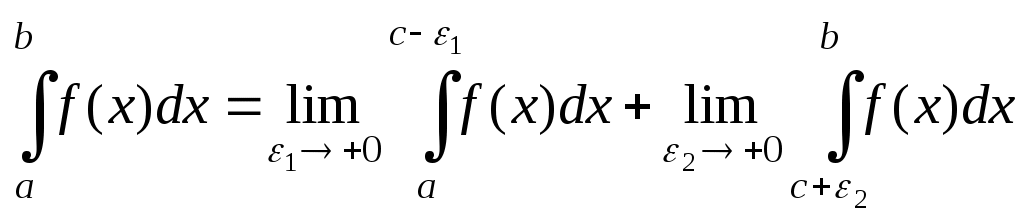 не ограничен  или функция не ограничена в окрестности одного из пределов интегрирования  , то по определению полагают , (5.9) . .Интегралы в левых частях равенств (5.9) и (5.10) называются несобственными интегралами. Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенств (5.9) и (5.10). Если же предел не существует, то несобственный интеграл называется расходящимся. 6. Вычисление площадей плоских фигур. Область называется правильной относительно оси  , если любая горизонтальная (вертикальная) прямая пересекает границу области не более чем в двух точках. Если область правильная относительно осей Ox и Oy, то она просто называется правильной областью. Области на рис. 7 правильные относительно оси  , на рис. 8 относительно оси  .   уy        d   c   О a b xOx Рис. 7. Рис. 8. Условимся дальше области, правильные относительно оси  , штриховать линиями, параллельными оси  .Если область G, правильная относительно оси , проектируется на ось Ox в отрезок , то ее граница разбивается на две линии: нижнюю границу области, задаваемую уравнением  , и верхнюю, задаваемую уравнением  . Тогда область G определяется системой неравенств а площадь фигуры, заключенной между кривыми и , на отрезке вычисляется по формуле . (5.11)Если область G, правильная относительно оси Ox, проектируется на ось Oy в отрезок  , то ее граница разбивается на две линии: левую границу области, задаваемую уравнением  , и правую, задаваемую уравнением  . В этом случае область G определяется системой неравенств а площадь фигуры, заключенной между кривыми и , на отрезке  вычисляется по формуле . (5.12)Если кривая, ограничивающая криволинейную трапецию, задана параметрическими уравнениями  , то площадь криволинейной трапеции ; (5.13)где и определяются из уравнений  и  . |