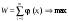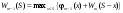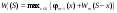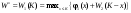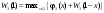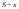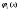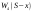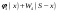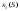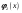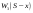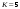Динамическое программирование. Динамическое программирование
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
Задача о распределении ресурсовПостановка задачиПусть имеется запас ресурсов  который нужно распределить между предприятиями который нужно распределить между предприятиями 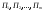 . Каждое из предприятий . Каждое из предприятий 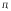 при вложении в него средств при вложении в него средств  приносит доход приносит доход 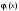 . Следует так распределить средства . Следует так распределить средства  между предприятиями, чтобы получить наибольший доход. между предприятиями, чтобы получить наибольший доход.Здесь задача не разделяется естественным образом на последовательно выполняемые шаги, поэтому введем такое разделение искусственно. Алгоритм решения задачиБудем считать первым шагом процесса вложение средств в 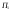 , вторым – в , вторым – в 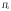 и т.д. и т.д.Управляемая система в данном случае – средства, которые распределяются. Состояние системы перед каждым шагом характеризуется одним числом  – наличным запасом еще не вложенных средств. Шаговыми управлениями являются средства – наличным запасом еще не вложенных средств. Шаговыми управлениями являются средства 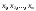 , выделяемые предприятиям. Требуется найти оптимальное управление, т.е. совокупность чисел , выделяемые предприятиям. Требуется найти оптимальное управление, т.е. совокупность чисел 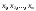 , при которой суммарный доход максимален , при которой суммарный доход максимален
Найдем для каждого  -го шага условный оптимальный выигрыш (от этого шага и до конца), если в начале -го шага условный оптимальный выигрыш (от этого шага и до конца), если в начале  -го шага был запас средств -го шага был запас средств  . Обозначим условный оптимальный выигрыш . Обозначим условный оптимальный выигрыш 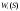 , а соответствующее ему условное оптимальное управление, то есть средства, вкладываемые в , а соответствующее ему условное оптимальное управление, то есть средства, вкладываемые в  -е предприятие, -е предприятие, 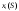 . .На последнем  -м шаге -м шаге 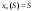 . Т.е. все оставшиеся нераспределенными средства вкладываются в последнее предприятие. Условный оптимальный выигрыш равен просто прибыли, получаемой последним предприятием . Т.е. все оставшиеся нераспределенными средства вкладываются в последнее предприятие. Условный оптимальный выигрыш равен просто прибыли, получаемой последним предприятием 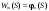 . .Перейдем к предпоследнему, 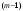 -му шагу. Пусть мы подошли к нему с запасом средств -му шагу. Пусть мы подошли к нему с запасом средств  . Обозначим . Обозначим 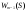 условный оптимальный выигрыш на двух последних шагах: условный оптимальный выигрыш на двух последних шагах: 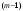 -м и -м и  -м. Если на -м. Если на 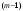 -м шаге -м шаге 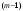 -му предприятию будут выделены средствах, то на последний шаг останется -му предприятию будут выделены средствах, то на последний шаг останется 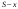 . Выигрыш на двух последних шагах составит . Выигрыш на двух последних шагах составит 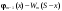 Нужно найти такое  , при котором этот выигрыш максимален , при котором этот выигрыш максимален
Далее оптимизируем 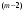 -й, -й, 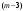 -й и т.д. шаги. Для любого -й и т.д. шаги. Для любого  -го шага будем находить условный оптимальный выигрыш за все шага с этого шага и до конца по формуле -го шага будем находить условный оптимальный выигрыш за все шага с этого шага и до конца по формуле
и соответствующее ему оптимальное управление 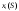 – то значение – то значение  , при котором этот максимум достигается. Уравнение (1.3) выражает принцип оптимальности Беллмана. , при котором этот максимум достигается. Уравнение (1.3) выражает принцип оптимальности Беллмана.Продолжая анализ шагов таким образом, дойдем до первого предприятия 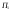 . Здесь нам не нужно варьировать значения . Здесь нам не нужно варьировать значения  , эта величина задана и равна , эта величина задана и равна  . Оптимальный выигрыш составит . Оптимальный выигрыш составит
То значение  , при котором достигается максимум (1.4), и есть оптимальное управление , при котором достигается максимум (1.4), и есть оптимальное управление 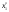 на первом шаге. После вложения средств на первом шаге. После вложения средств 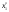 в первое предприятие их останется в первое предприятие их останется 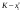 . Используя найденную ранее зависимость условно оптимального управления для второго шага . Используя найденную ранее зависимость условно оптимального управления для второго шага 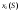 , находим безусловное оптимальное управление для второго шагa, , находим безусловное оптимальное управление для второго шагa, 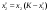 , затем, аналогично, для третьего шага , затем, аналогично, для третьего шага 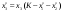 , и т.д. , и т.д.Пример 1.3. Пусть исходный запас средств 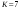 и требуется его распределить между четырьмя предприятиями и требуется его распределить между четырьмя предприятиями 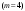 . Количество средств, которое можно вложить в каждое предприятие кратно . Количество средств, которое можно вложить в каждое предприятие кратно 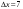 , то есть можно вложить только целое количество средств, кроме того объем средств, вкладываемых в каждое предприятие не должен превышать , то есть можно вложить только целое количество средств, кроме того объем средств, вкладываемых в каждое предприятие не должен превышать 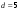 единиц. Функции дохода заданы в таблице 1.2 единиц. Функции дохода заданы в таблице 1.2Таблица 1.2
Математическая модель задачи Требуется найти такие объемы средств, выделяемые предприятиям 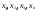 чтобы весь запас средств был распределен: чтобы весь запас средств был распределен: 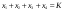 , а общий выигрыш был максимален , а общий выигрыш был максимален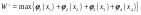 Построение условно оптимальных решений Проведем условную оптимизацию, начиная с последнего 4-го шага. Надо рассмотреть все возможные значения  и найти соответствующие и найти соответствующие 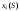 и и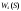 . К последнему шагу мы должны подойти с запасом средств . К последнему шагу мы должны подойти с запасом средств 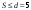 . Па последнем шаге все средства выделяются четвертому предприятию, поэтому . Па последнем шаге все средства выделяются четвертому предприятию, поэтому 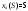 , ,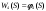 , то есть условный оптимальный выигрыш на 4-м шаге равен доходу 4-го предприятия от вложенных в него средств. , то есть условный оптимальный выигрыш на 4-м шаге равен доходу 4-го предприятия от вложенных в него средств.Рассмотрим третий шаг. Пусть объем распределяемых средств на третьем шаге 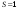 . Количество средств . Количество средств  , вкладываемых в третье предприятие, может иметь значения 0 и 1. Согласно (1.2) , вкладываемых в третье предприятие, может иметь значения 0 и 1. Согласно (1.2)
Вычислим значения выражения в фигурных скобках: при 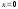 , , 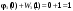 и при и при 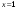 , , 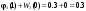 Отсюда видно, что правая часть (1.5) максимальна при 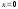 , Значит , Значит 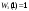 , , 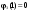 . Для построения условного оптимального решения на третьем шаге следует рассмотреть все возможные значения для . Для построения условного оптимального решения на третьем шаге следует рассмотреть все возможные значения для  , то есть , то есть 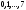 . Соответствующие расчеты разместим в табл. 1.3. . Соответствующие расчеты разместим в табл. 1.3.Таблица 1.3. Условно оптимальные решения для третьего шага.
Поиск условно оптимальных решений состоит в нахождении максимального значения в столбце 6 табл.1.2 для каждого  . Эти максимальные значения выделены, выделены также и соответствующие им значения . Эти максимальные значения выделены, выделены также и соответствующие им значения  . Найденные условно оптимальные решения выписаны в столбцах 7 и 8. . Найденные условно оптимальные решения выписаны в столбцах 7 и 8.Отметим, что в некоторых случаях максимум достигается при нескольких значениях  , однако для динамического программирования это не является большой проблемой, так как важно лишь значение максимума. , однако для динамического программирования это не является большой проблемой, так как важно лишь значение максимума.При построении условно оптимальных решений для 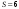 и 7 учитываем ограничение, что объем ресурсов, выделяемых одному предприятию, не превышает и 7 учитываем ограничение, что объем ресурсов, выделяемых одному предприятию, не превышает 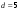 . Это значит, что . Это значит, что 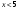 и и 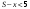 Вычисления по нахождению условно оптимального решения на втором шаге поместим в табл.1.4. Значения выигрыша на втором шаге берем из исходной табл.1.2, а условно оптимальный выигрыш на третьем шаге 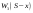 из табл. 1.3. из табл. 1.3.Таблица 1.4.Условно оптимальные решения для второго шага
При построении условного оптимального управления на первом шаге рассматриваем только один случай 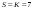 . . Таблица 1.5. Результаты условной оптимизации. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | 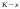 | 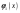 | 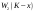 | 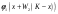 | 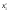 | 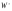 |
| 0 | 7 | 0 | 3.6 | 3.6 | 5 | 4.1 |
| 1 | 6 | 0.1 | 3.4 | 3.5 | | |
| 2 | 5 | 0.5 | 2.9 | 3.4 | | |
| 3 | 4 | 1.2 | 2.4 | 3.6 | | |
| 4 | 3 | 1.8 | 2.1 | 3.9 | | |
| 5 | 2 | 2.5 | 1.6 | 4.1 | | |
Нахождение безусловного оптимального управления
Результаты оптимизации по всем шагам сведем в табл.1.6.
Таблица 1.6. Результаты условной оптимизации 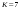
 |  |  |  |  | |||||
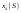 | 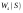 | 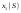 | 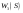 | 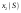 | 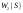 | 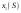 | 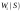 | ||
| 1 | 1 | 1.0 | 0 | 1.0 | 0 | 1.0 | | | |
| 2 | 2 | 1.2 | 1 | 1.3 | 1 | 1.6 | | | |
| 3 | 3 | 1.3 | 2 | 1.6 | 2 | 2.1 | | | |
| 4 | 4 | 1.3 | 3 | 2.3 | 2 | 2.4 | | | |
| 5 | 5 | 1.3 | 3 | 2.5 | 1 | 2.9 | | | |
| 6 | | | 3, 4 | 2.6 | 2 | 3.4 | | | |
| 7 | | | 4, 5 | 2.7 | 2 | 3.6 | 5 | 4.1 | |
В табл.1.6 S означает запас ресурсов, с которым мы приходим к очередному шагу. Из таблицы видно, что безусловный оптимальный выигрыш есть
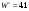 , при этом первому предприятию следует выделить 5 единиц ресурсов из 7. Значит, в началt второго шага мы будем иметь 7-5 = 2 единицы ресурсов. Из строки таблицы для
, при этом первому предприятию следует выделить 5 единиц ресурсов из 7. Значит, в началt второго шага мы будем иметь 7-5 = 2 единицы ресурсов. Из строки таблицы для 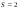
 находим, что второму предприятию следует выделить 1 единицу. К началу третьего шага останется 2-1 = 1 единица ресурсов. При
находим, что второму предприятию следует выделить 1 единицу. К началу третьего шага останется 2-1 = 1 единица ресурсов. При 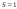 третье предприятие не получает ничего. К началу четвертого шага остается 1 единица ресурсов, которая выделяется четвертому предприятию.
третье предприятие не получает ничего. К началу четвертого шага остается 1 единица ресурсов, которая выделяется четвертому предприятию.Итак, оптимальное управление есть
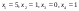 .
.В табл.1.6 эти управления выделены подчеркиванием.