Динамическое программирование. Динамическое программирование
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
1. 2. Задачи, решаемые методом динамического программированияЗадача определения кратчайшего расстоянияПостановка задачи.Пусть задана достаточно связная сеть, на которой каждому звену  поставлено в соответствие некоторое неотрицательное число поставлено в соответствие некоторое неотрицательное число 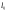 - его длина. Необходимо найти кратчайшие расстояния по сети от каждой точки до всех остальных и соответствующие пути по которым они проходят. - его длина. Необходимо найти кратчайшие расстояния по сети от каждой точки до всех остальных и соответствующие пути по которым они проходят.Пронумеруем точки сети в любом порядке (слева направо, сверху вниз) и укажем длину каждого звена. Две точки назовем соседними, если они непосредственно соединены связью. Это, например, точки 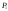 и и 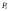 P2, P2, 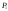 и и 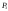 и т.д. и т.д. Для решения задачи используется метод динамического программирования. Разобьем процесс на n этапов. На каждом этапе отыскиваем кратчайшее расстояние не от фиксированной точки до всех остальных, а расстояние от всех остальных до фиксированной через соседние точки. Связь, через – которую проходит кратчайшее расстояние, после каждого шага отмечаем стрелкой. Для удобства точки сети обозначим кружками. Алгоритм решения задачи о нахождении кратчайшего пути.Шаг 1. Фиксируем точку 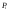 , до которой необходимо рассчитать кратчайшее расстояние от всех остальных, и в кружке обозначим эту точку, записываем нуль, так как расстояние от точки , до которой необходимо рассчитать кратчайшее расстояние от всех остальных, и в кружке обозначим эту точку, записываем нуль, так как расстояние от точки 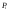 до нее самой равно нулю. Это число, которое для других точек отлично от нуля, назовем характеристикой точки. до нее самой равно нулю. Это число, которое для других точек отлично от нуля, назовем характеристикой точки.Шаг 2. Определяем соседние точки по отношению к фиксированной. В кружках, обозначающих эти точки. Записываем их характеристики  Cij=0+lij и на связях ставим стрелки, направленные в сторону точки Cij=0+lij и на связях ставим стрелки, направленные в сторону точки 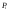 . .Шаг 3. Отмечаем точку 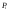 символом V, обозначающим, что операции над ней закончены. символом V, обозначающим, что операции над ней закончены.Шаг 4. Переходим к любой соседней с 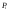 точке, для которой характеристики уже найдены. Пусть это точка точке, для которой характеристики уже найдены. Пусть это точка 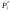 . Определяем соседние с ней точки и рассчитываем для них характеристики как сумму . Определяем соседние с ней точки и рассчитываем для них характеристики как сумму 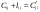 . .Шаг 5. Точку 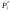 отмечаем знаком V и переходим к шагу 4 алгоритма. отмечаем знаком V и переходим к шагу 4 алгоритма.Шаг 6. При определении 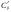 для соседних точек для соседних точек 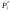 может оказаться, что для некоторых из них может оказаться, что для некоторых из них 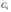 уже рассчитаны. В этом случае уже рассчитаны. В этом случае 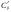 сравниваем с сравниваем с 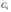 . .Если 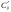   для всех таких точек, то для всех таких точек, то  остаются без изменения; точку остаются без изменения; точку 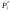 отмечаем знаком V и переходим к Ш.4 алгоритма. Если отмечаем знаком V и переходим к Ш.4 алгоритма. Если 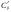 < <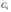 , то , то 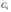 заменяем на заменяем на 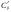 , соответственно изменяется связь, через которую проходит кратчайшее расстояние. Точку , соответственно изменяется связь, через которую проходит кратчайшее расстояние. Точку 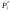 отмечаем знаком V только в том случае, если точка, у которой изменилась характеристика, не была ранее отмечена. отмечаем знаком V только в том случае, если точка, у которой изменилась характеристика, не была ранее отмечена.Шаг 7. Если изменилась характеристика отмеченной точки, то пересчитываем характеристики точек, соседней с ней, а затем отмечаем точку 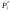 и переходим к Ш.4 алгоритма. и переходим к Ш.4 алгоритма.Шаг 8. Процесс продолжаем до тех пор, пока не будут отмечены все точки. После этого выписываем кратчайшие расстояния (характеристики точек) и маршруты, по которым они проходят. На этом первый этап заканчивается. Шаг 9. Переходим к следующему этапу, начиная с Ш.1 алгоритма. Расчет продолжаем до тех пор, пока не будут определены кратчайшие расстояния от всех точек до каждой из них. Пример 1.1. Определить кратчайшее расстояние от всех точек до точки 8, изображенному на рисунке 1.1. Где кружки означают точки; цифры стоящие в кружках – их номера; прямолинейные отрезки – связи; числа, стоящие над связями, - их длину; числа, стоящие возле точек, - их характеристики, а стрелки указывают маршрут, по которому проходит кратчайшее расстояние. Решение. Записываем возле точки 8 характеристику – нуль. Определим характеристики точек 4, 6 и 7, соседних с ней, и стрелкой возле каждой точки указываем направление кратчайшей связи. Точку 8 отмечаем знаком V. Рассмотрим точку 7. Определим характеристики точек 5, 6 и 8, соседней с ней. Характеристику точки 5, равную 39, запишем около нее и укажем стрелкой направление. Для точек 6 и 8 новые характеристики соответственно равны 39 > 18, 54 > 0. Следовательно, ранее определенные для них характеристики оставляем без изменения. Точку 7 отмечаем знаком V. Рассмотрим точку 6. Соседними являются точки 2, 4, 5, 7 и 8. Характеристику точки 2, равную 23, запишем около нее и укажем направление. Для точки 4 новая характеристика 26 > 9, для точки 5 характеристика 26 < 39. Поэтому запишем новую характеристику и изменим направление кратчайшей связи. Для точек 7 и 8 новые характеристики соответственно равны 30 > 27 и 36 > 0, т.е. характеристики оставим без изменения. Точку 6 отмечаем знаком V. Рассмотрим точку 4 и ее соседние точки 1, 6 и 8. Характеристику точки 1, равную 11, запишем около нее и укажем направление. Для точки 6 новая характеристика 17 < 18. Изменяем характеристику и направление для точки 6. 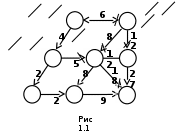 Так как точка 6 отмечена знаком V, то пересчитываем характеристики точек 2, 5, 7, 8, соседних с ней, и в случае необходимости изменяем направление. Для точки 2 новая характеристика 22 < 23, следовательно, изменяем характеристику; характеристика точки 5, 25 < 26 – изменяем характеристику; для точек 7 и 8 соответственно имеем: 29 > 27 и 35 > 0 –характеристики не меняем. Точку 4 отмечаем знаком V. Рассмотрим точку 5 и соседние точки 3, 6 и 7. Характеристику точки 3, равную 31, запишем около нее и укажем направление. Характеристики точек 6 и 7 остаются без изменения. Точку 5 отмечаем знаком V. Характеристики точки 3 и соседних точек 2 и 5 остаются без изменения. Отмечаем точку 3 знаком V. Рассмотрим точку 2 и соседние с ней точки 1, 3 и 6. Характеристики точек 1 и 6 остаются без изменения. Для точки 3 характеристика 26 < 31, следовательно, изменяем характеристику и направление, а так как эта точка уже отмечена, то пересчитываем характеристику соседней с ней точки 5. Характеристика точки 5 осталась без изменения. Отмечаем точку 2 знаком V. Рассмотрим точку 1 и соседние точки 2 и 4. Для точки 2 новая характеристика 13 < 22 – изменяем характеристику и направление. Точка 2 ранее отмечена, поэтому пересчитываем характеристики соседней с ней точек 3 и 6. Для точки 3 новая характеристика 17 < 26 – изменяем характеристику и пересчитываем характеристику точки 5. Так как новая характеристика этой точки 23 < 25, то изменяем характеристику и направление точки и пересчитываем характеристики точек 6 и 7. Они остались без изменения. Характеристика точки 6 остается без изменения и при пересчете ее со стороны точки 2. Для точки 4 характеристика не изменяется. Точку 1 отмечаем знаком V. Все точки отмечены, поэтому первый этап закончен. Получено оптимальное решение: величина окончательной характеристики соответствует кратчайшему расстоянию до точки 8, стрелка указывает соседнюю точку, через которую это расстояние проходит. Таблица 1.1
Записываем оптимальное решение в таблицу 8 и переходим к очередному этапу. Процесс продолжается до тех пор, пока не будут рассчитаны кратчайшие расстояния от всех точек до каждой из них. Замечание. Необходимо отметить, что числа lij можно интерпретировать по-разному. Они могут означать расстояние, стоимость, себестоимость, время и т.д. |
