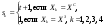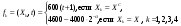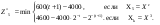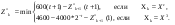Динамическое программирование. Динамическое программирование
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
Задача о замене оборудованияПостановка задачиЗамена оборудования – важная экономическая проблема. Задача состоит в определении оптимальных сроков замены старого оборудования (станков, производственных зданий и т. п.). Старение оборудования включает его физический и моральный износ, в результате чего растут производственные затраты, затраты на ремонт и обслуживание, снижаются производительность труда, ликвидная стоимость. Критерием оптимальности являются, как правило, либо прибыль от эксплуатации оборудования (задача максимизации), либо суммарные затраты на эксплуатацию в течениепланируемого периода (задача минимизации). При построении модели задачи принято считать, что решение о замене выносится в начале каждого промежутка эксплуатации (например, в начале года) и что в принципе оборудование можно использовать неограниченно долго. Основная характеристика оборудования – параметр состояния – его возраст  . .При составлении динамической модели замены процесс замены рассматривают как  -шаговый, разбивая весь период эксплуатации на -шаговый, разбивая весь период эксплуатации на  шагов. Возможное управление на каждом шаге характеризуется качественными признаками, например, шагов. Возможное управление на каждом шаге характеризуется качественными признаками, например, 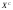 (сохранить оборудование), (сохранить оборудование), 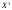 (заменить) и (заменить) и 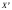 (сделать ремонт). (сделать ремонт). Пример. Оборудование эксплуатируется в течение 5 лет, после этого продается. В начале каждого года можно принять решение сохранить оборудование или заменить его новым. Стоимость нового оборудования 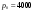 руб. После руб. После  лет эксплуатции лет эксплуатции 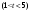 оборудование можно продать за оборудование можно продать за 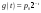 рублей (ликвидная стоимость). Затраты на содержание в течение года зависят от возраста рублей (ликвидная стоимость). Затраты на содержание в течение года зависят от возраста  оборудования и равны оборудования и равны 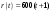 (все цены условные). Определить оптимальную стратегию эксплуатации оборудования, чтобы суммарные затраты с учетом начальной покупки и заключительной продажи были минмальны. (все цены условные). Определить оптимальную стратегию эксплуатации оборудования, чтобы суммарные затраты с учетом начальной покупки и заключительной продажи были минмальны. Решение. Способ деления управления на шаги естественный, по годам, 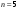 . Параметр состояния – возраст машины . Параметр состояния – возраст машины 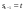 , , 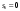 – машина новая в начале первого года эксплуатации. Управление на каждом шаге зависит от двух переменных – машина новая в начале первого года эксплуатации. Управление на каждом шаге зависит от двух переменных 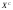 и и 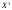 . Уравнения состояний зависят от управления: . Уравнения состояний зависят от управления:
В самом деле, если к 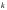 -му шагу -му шагу 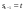 , то при сохранении машины , то при сохранении машины 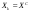 через год возраст машины увеличится на 1. Если машина заменяется новой через год возраст машины увеличится на 1. Если машина заменяется новой 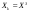 , то это означает, что к началу , то это означает, что к началу 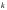 -ro шага ее возраст -ro шага ее возраст 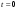 , а после года эксплуатации , а после года эксплуатации 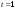 , т.е. , т.е.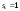 . .Показатель эффективности 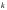 -го шага: -го шага:
(При 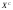 затраты только на эксплуатацию машины возраста затраты только на эксплуатацию машины возраста  , при , при 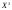 машина продается ( машина продается (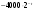 ), покупается новая ( ), покупается новая (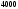 ) и эксплуатируется в течение первого года ( ) и эксплуатируется в течение первого года (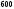 ), общие затраты равны ( ), общие затраты равны (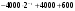 )). )).Пусть 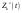 – условные оптимальные затраты на эксплуатацию машины, начиная с – условные оптимальные затраты на эксплуатацию машины, начиная с 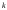 -го шага до конца, при условии, что к началу -го шага до конца, при условии, что к началу 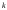 -го шага машина имеет возраст -го шага машина имеет возраст  лет. Запишем для функций лет. Запишем для функций 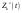 уравнение Беллмана (1.3), заменив задачу максимизации на задачу минимизации: уравнение Беллмана (1.3), заменив задачу максимизации на задачу минимизации:
Величина 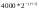 – стоимость машины возраста – стоимость машины возраста  лет (по условию машина после 5 лет эксплуатации продается). лет (по условию машина после 5 лет эксплуатации продается).
Из определения функций 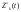 следует следует 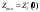 Дадим геометрическое решение этой задачи. На оси абсцисс будем откладывать номер шага 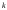 , на оси ординат – возраст , на оси ординат – возраст  машины. Точка машины. Точка 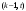 на плоскости соответствует началу на плоскости соответствует началу 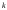 -то года эксплуатации машины возраста -то года эксплуатации машины возраста  лет. Перемещение на графике в зависимости от принятого управления на лет. Перемещение на графике в зависимости от принятого управления на 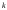 -м шаге показано на рис. 1.6. -м шаге показано на рис. 1.6.Состояние начала эксплуатации машины соответствует точке 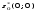 , конец – точкам , конец – точкам 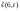 . Любая траектория, переводящая точку . Любая траектория, переводящая точку 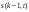 из из 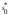 в в 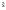 , состоит из отрезков – шагов, соответствующих годам эксплуатации. Надо выбрать такую траекторию, при которой затраты на эксплуатацию машины окажутся минимальными. , состоит из отрезков – шагов, соответствующих годам эксплуатации. Надо выбрать такую траекторию, при которой затраты на эксплуатацию машины окажутся минимальными. Рис. 1.6. Перемещение на графике в зависимости от решения, принятого на k-ом шаге 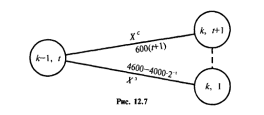 Над каждым отрезком, соединяющим точки 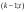 и и 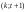 , запишем соответствующие управлению , запишем соответствующие управлению 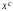 затраты, найденные из (1.7): затраты, найденные из (1.7): 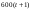 , а над отрезком, соединяющим точки , а над отрезком, соединяющим точки 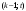 и и 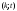 , запишем затраты, соответствующие управлению , запишем затраты, соответствующие управлению 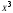 , т.е. , т.е. 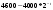 . Таким образом мы разметим все отрезки, соединяющие точки на графике, соответствующие переходам из любого состояния . Таким образом мы разметим все отрезки, соединяющие точки на графике, соответствующие переходам из любого состояния 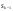 в состояние в состояние 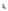 (рис. 1.7). Например, над отрезками, соединяющими точки (рис. 1.7). Например, над отрезками, соединяющими точки 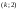 и и 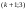 , стоит число , стоит число 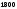 , что соответствует затратам на эксплуатацию в течение каждого года машины возраста , что соответствует затратам на эксплуатацию в течение каждого года машины возраста 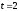 лет, а над отрезками, соединяющими лет, а над отрезками, соединяющими 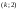 и и 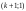 , стоит число 3600 – это сумма затрат на покупку машины и эксплуатацию новой машины в течение года без "затрат" (выручки) за проданную машину возраста t лет. Следует учесть, что , стоит число 3600 – это сумма затрат на покупку машины и эксплуатацию новой машины в течение года без "затрат" (выручки) за проданную машину возраста t лет. Следует учесть, что 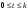 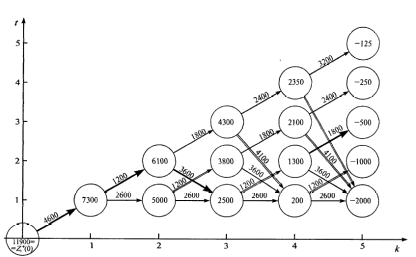  Рис. 1.7. График переходов из одного состояния в другое Проведем на размеченном графе состояний (см. рис. 1.7) условную оптимизацию. V шаг. Начальные состояния – точки 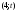 , конечные , конечные 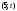 . В состояниях . В состояниях 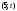 машина продается, условный оптимальный доход от продажи равен машина продается, условный оптимальный доход от продажи равен 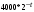 , но поскольку целевая функция связана с затратами, то в кружках точек , но поскольку целевая функция связана с затратами, то в кружках точек 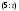 поставим величину дохода со знаком минус. поставим величину дохода со знаком минус.Анализируем, как можно попасть из каждого начального состояния в конечное на V шаге. Состояние 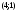 Из него можно попасть в состояние Из него можно попасть в состояние 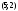 , затратив на эксплуатацию машины 1200 и выручив затем от продажи 1000, т.е. суммарные затраты равны 200, и в состояние , затратив на эксплуатацию машины 1200 и выручив затем от продажи 1000, т.е. суммарные затраты равны 200, и в состояние 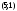 с затратами с затратами 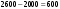 . Значит, если к последнему шагу система находилась в точке . Значит, если к последнему шагу система находилась в точке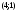 , то следует идти в точку (5; 2) (укажем это направление двойной стрелкой), а неизбежные минимальные затраты, соответствующие этому переходу, равны 200 (поместим эту величину , то следует идти в точку (5; 2) (укажем это направление двойной стрелкой), а неизбежные минимальные затраты, соответствующие этому переходу, равны 200 (поместим эту величину 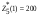 в кружке точки в кружке точки 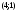 . Состояние . Состояние 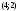 . Из него можно попасть в точку . Из него можно попасть в точку 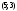 с затратами 1800-500=1300 и в точку с затратами 1800-500=1300 и в точку 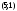 с затратами 3600-2000=1600. Выбираем первое управление, отмечаем его двойной стрелкой, а с затратами 3600-2000=1600. Выбираем первое управление, отмечаем его двойной стрелкой, а 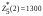 проставляем в кружке точки проставляем в кружке точки 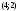 . Рассуждая таким же образом для каждой точки предпоследнего шага, мы найдем для любого исхода IV шага оптимальное управление на V шаге, отметим его на рис. 1.7 двойной стрелкой. Далее планируем IV шаг, анализируя каждое состояние, в котором может оказаться система в конце III шага с учетом оптимального продолжения до конца процесса, т.е. решаем для всех . Рассуждая таким же образом для каждой точки предпоследнего шага, мы найдем для любого исхода IV шага оптимальное управление на V шаге, отметим его на рис. 1.7 двойной стрелкой. Далее планируем IV шаг, анализируя каждое состояние, в котором может оказаться система в конце III шага с учетом оптимального продолжения до конца процесса, т.е. решаем для всех 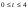 при при  уравнения (1.6). Например, если начало IV шага соответствует состоянию (3; 1), то при управлении уравнения (1.6). Например, если начало IV шага соответствует состоянию (3; 1), то при управлении 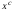 система переходит в точку система переходит в точку 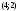 , затраты на этом шаге 1200, а суммарные затраты за два последних шага равны 1200+1300=2500. При управлении , затраты на этом шаге 1200, а суммарные затраты за два последних шага равны 1200+1300=2500. При управлении 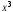 затраты за два шага равны 2600+200=2800. Выбираем минимальные затраты 2500, ставим их в кружок точки (3; 1), а соответствующие управления на этом шаге помечаем двойной стрелкой, ведущей из состояния (3; 1), в состояние (4; 2). Так поступаем для каждого состояния затраты за два шага равны 2600+200=2800. Выбираем минимальные затраты 2500, ставим их в кружок точки (3; 1), а соответствующие управления на этом шаге помечаем двойной стрелкой, ведущей из состояния (3; 1), в состояние (4; 2). Так поступаем для каждого состояния 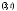 (см. рис. 1.7). (см. рис. 1.7).Продолжая условную оптимизацию III, II и I шагов, мы получим на рис. 1.7 следующую ситуацию: из каждой точки (состояния) выходит стрелка, указывающая, куда следует перемещаться в данном шаге, если система оказалась в этой точке, а в кружках записаны минимальные затраты на переход из этой точки в конечное состояние. На каждом шаге графически решались уравнения (1.6). После проведения условной оптимизации получим в точке (0; 0) минимальные затраты на эксплуатацию машины в течение 5 лет с последующей продажей: 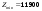 . Далее строим оптимальную траекторию, перемещаясь из точки ,$0(0; 0) по двойным стрелкам в s Получаем набор точек: . Далее строим оптимальную траекторию, перемещаясь из точки ,$0(0; 0) по двойным стрелкам в s Получаем набор точек: 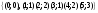 , который соответствует оптимальному управлению , который соответствует оптимальному управлению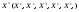 . Оптимальный режим эксплуатации состоит в том, чтобы заменить машину новой в начале 3-го года. . Оптимальный режим эксплуатации состоит в том, чтобы заменить машину новой в начале 3-го года.Таким образом, размеченный график (сеть) позволяет наглядно интерпретировать расчетную схему и решить задачу методом ДП. Как уже отмечалось, модели и вычислительная схема ДП очень гибки в смысле возможностей включения в модель различных модификаций задачи. Например, аналогичная задача может быть рассмотрена для большого числа вариантов управления, "ремонт", "капитальный ремонт" и т. д. Можно рассматривать замену оборудования новым с учетом технического прогресса, можно учесть изменения в затратах на эксплуатацию оборудования после его ремонта, в зависимости от года эксплуатации (дороже, дешевле). Все эти факторы можно учитывать вычислительной схемой ДП. |