Динамика систем
 Скачать 2.39 Mb. Скачать 2.39 Mb.
|
Определение собственных значений и собственных векторов матрицы коэффициентов системы ДУОпределяем собственные значения и собственные вектора матрицы коэффициентов системы ДУ (таблица 4.2), используя имеющуюся на кафедре «Электропоезда и локомотивы» программу на языке Pascal, реализующую QR-алгоритмы. Полученные значения приведены в таблицах 5.1 и 5.2. Собственные значения матрицы коэффициентов системы д.у. Таблица 5.1
Из таблицы 5.1 видно, что собственные значения являются комплексным числом. Действительная часть этого числа – степень затухания α, а мнимая–собственная круговая частота колебаний малодемпфированной системы ω𝑐 . Знак «–» у степени затухания свидетельствует о том, что колебания исследуемой системы устойчивы. Из сравнения собственных и парциальных частот колебаний по координатам  , видно, что они практические совпадают. Это объясняется принятым при исследовании малым значением относительного коэффициента затухания n = 0,05. , видно, что они практические совпадают. Это объясняется принятым при исследовании малым значением относительного коэффициента затухания n = 0,05.Собственные вектора матрицы коэффициентов системы д.у. Таблица 5.2
Исследование собственных колебаний модели с помощью собственных значений и собственных векторов матрицы коэффициентов системы ДУ. Для исследования свободных колебаний вторым методом необходимо, используя полученные значения собственных векторов, рассчитать коэффициент распределения амплитуд обобщённых координат и сдвиги по фазе между ними. Для этого необходимо от алгебраической формы представления комплексных чисел перейти к показательной:  Амплитуда А и фазу  комплексного числа можно определить по следующей формуле: комплексного числа можно определить по следующей формуле: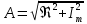  Определим в начале амплитуду комплексных чисел. Значения будем округлять до третьего знака после запятой. Амплитуды собственных векторов матрицы коэффициентов системы д.у. Таблица 6.1
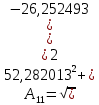 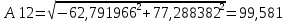      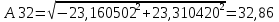 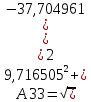 Заполним таблицу 6.1 полученными значениями амплитуд и сведем её в таблицу 6.2. Значения амплитуд собственных векторов матрицы коэффициентов системы д.у. Таблица 6.2
Пронормируем значения Аik по столбцам в матрице, для этого необходимо значения Аik каждого столбца поделить на максимальное значение в этом столбце. Получим матрицу распределения μik. Матрица коэффициентов распределения амплитуд. Таблица 6.3
Заполним матрицу коэффициентов распределения амплитуд. Значения матрицы коэффициентов распределения амплитуд. Таблица 6.4
Как видно из этой матрицы, влияние колебаний по координатам, 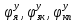 составляет: составляет: — на 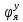 , координату крутильных колебаний якоря: , координату крутильных колебаний якоря:координата крутильных колебаний зубчатого колеса 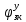 на 11,1% на 11,1% координата крутильных колебаний колесной пары 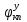 на 18%; на 18%; координату крутильных колебаний якоря 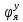 на 100%. на 100%.— на 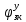 , координата крутильных колебаний зубчатого колеса: , координата крутильных колебаний зубчатого колеса:координата крутильных колебаний зубчатого колеса 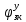 на 100%; на 100%;координата крутильных колебаний колесной пары 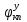 на 12,5%; на 12,5%;координату крутильных колебаний якоря 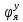 на 14,8%. на 14,8%.— на 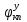 , координату крутильных колебаний якоря: , координату крутильных колебаний якоря:координата крутильных колебаний зубчатого колеса 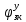 на 41,6%; на 41,6%;координата крутильных колебаний колесной пары 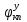 на 33%; на 33%;координату крутильных колебаний якоря 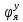 на 100%. на 100%.Далее найдем сдвиги по фазе φiт между этими координатами (Таблица6.5). Матрица фазовых сдвигов. Таблица 6.5
Определим фазовую характеристику φiт по формуле : 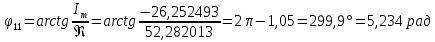  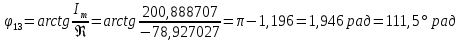 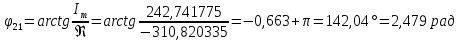      Значения фазовых сдвигов. Таблица 6.6
При выполнении исследований свободных колебаний вторым методом, используя полученные  , ,  , ,  , ,  , с помощью принципа суперпозиции вычисляются зависимости координат от времени , с помощью принципа суперпозиции вычисляются зависимости координат от времени  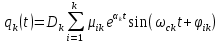 где  – произвольная постоянная – произвольная постоянная k = 3 Для каждого из видов колебаний запишем: 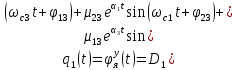      Округлив ωcт, αт до третьего знака, будем иметь следующие выражения:     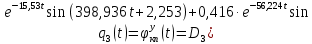 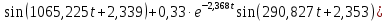 Произвольные постоянные 𝐷1, 𝐷2 и 𝐷3 определяем из условий: 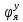 (0) = 0,01 (0) = 0,01 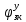 (0) = 0,01 (0) = 0,01 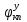 (0) = 0,01 (0) = 0,01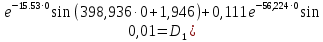       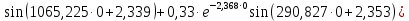 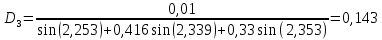 В окончательном виде записываем выражения:     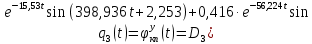 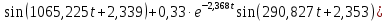 Графики этих зависимостей приведены на рисунках 6.1-6.3:     T  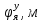  Рис.6.1 Реализация процесса крутильных колебаний якоря при задании начальных условий на его вертикальное перемещение 0,01м  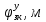 Начальная амплитуда равна 0.01. Т = 0,017 с, тогда f =58,82 Гц      T2 T1   Рис.6.2 Реализация процесса крутильных колебаний зубчатого колеса при задании начальных условий на его вертикальное перемещение 0,01м Начальная амплитуда равна 0.01. Т1 = 0,0061 с, тогда f1 = 163,93 Гц Т2 = 0,018 с, тогда f2 = 55,55 Гц     T  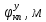  Рис.6.3 Реализация процесса крутильных колебаний колесной пары при задании начальных условий на его вертикальное перемещение 0,01м Начальная амплитуда равна 0.01. Т = 0,019 с, тогда f = 52,63 Гц Получившееся собственные частоты колебаний близки к парциальным частотам, полученным в пункте 2. Таким образом, нарушений в работе QR-алгоритма не наблюдается. Файлы с результатами расчёта QR-алгоритма и результаты расчёта зависимостей обобщённых координат от времени  приведены в приложении Б. приведены в приложении Б.Анализ результатов выполненных исследований. В курсовой работе проводили исследование двумя различными способами, в результате которых делаем следующий вывод: На основании построения графиков зависимостей по методу Рунге-Кутта IV порядка можно сделать вывод, что крутильные колебания якоря , зубчатого колеса и колесной пары в той или иной мере взаимосвязаны. Матрица коэффициентов распределения амплитуд μik , основанная на результатах расчётов по QR-алгоритму также подтверждает это. |