Динамика систем
 Скачать 2.39 Mb. Скачать 2.39 Mb.
|
|
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА» (РУТ(МИИТ))  Кафедра «Электропоезда и локомотивы» КУРСОВАЯ РАБОТА Исследование свободных колебаний упрощенных моделей э.п.с. «ДИНАМИКА СИСТЕМ» Выполнил: Студент группы ТПЭ-312 Кудрявцев В. А. «____» _______________ 2021 г. Принял: Доц. Васильев А.П. «____» _______________ 2021 г. Москва 2021 СодержаниеВведение……………………………………………………………………4 Цель работы……………………………………………………………….6 1.Кинематическая схема и дифференциальные уравнения свободных колебаний исследуемой модели. 7 1.1 Определение величин коэффициентов затухания 9 2.Приведение системы уравнений к форме Коши и понижение порядка системы 10 3. Исследование свободных колебаний модели путём решения системы ДУ методом Рунге-Кутта IV порядка в пакете Mathcad. 13 4. Составление матрицы коэффициентов системы ДУ 20 5.Определение собственных значений и собственных векторов матрицы коэффициентов системы ДУ 22 6.Исследование собственных колебаний модели с помощью собственных значений и собственных векторов матрицы коэффициентов системы ДУ. 24 7.Анализ результатов выполненных исследований. 32 В курсовой работе проводили исследование двумя различными способами, в результате которых делаем следующий вывод: 32 На основании построения графиков зависимостей по методу Рунге-Кутта IV порядка можно сделать вывод, что крутильные колебания якоря , зубчатого колеса и колесной пары в той или иной мере взаимосвязаны. Матрица коэффициентов распределения амплитуд μik , основанная на результатах расчётов по QR-алгоритму также подтверждает это. 32 Вывод 33  Введение При движении железнодорожного экипажа (локомотива, вагона) по рельсовому пути из-за неровностей на поверхности катания рельсов и бандажей, переменности параметров пути, возникают колебания экипажа, которые сопровождаются динамическими явлениями, ухудшающими работоспособность системы «экипаж – путь». При проектировании экипажей, стремиться снизить уровень колебаний, обеспечивая выполнение требований к показателям динамических качеств. Определение характеристик колебательных процессов, возникающих в экипаже при движении по рельсовому пути, на основе которых могут быть решены задачи по созданию системы, удовлетворяющей необходимым качественным критериям, производится путем теоретического решения задачи о колебаниях механической системы «экипаж-путь». Для составления уравнений колебаний удобно использовать общее уравнение динамики системы в обобщенных силах или уравнение Лагранжа второго рода. Силой инерции называют силу, дополнительно прилагаемую к материальной точке, равную произведению её массы на ускорение и направленную в противоположную сторону. В соответствии с принципом Даламбера после приложения сил инерции система находится в равновесии. Согласно общему уравнению динамики, сумма обобщённых активных сил и обобщённых сил инерции равна нулю. Уравнение колебаний рельсовых экипажей удобно составлять, используя формулу Лагранжа только для вычисления обобщённых сил инерции, а упругую и диссипативную части обобщенной активной силы лучше находить исходя из определения обобщённой силы на основе понятия возможной мощности. При этом отпадет необходимость использования квадратов малых отклонений обобщенных координат, входящий в выражение потенциальной энергии системы. Цель работы: Исследование свободных колебаний и взаимодействия элементов кинематических схем упрощенной модели э.п.с. Кинематическая схема и дифференциальные уравнения свободных колебаний исследуемой модели.Схема исследуемой модели представлена на рисунке 1.1: 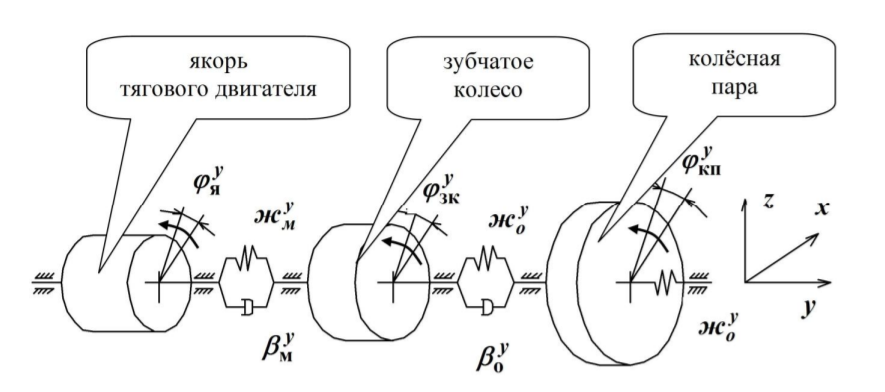 Рисунок 1.1. Модель подвижного состава для исследования крутильных колебаний системы колёсная пара – зубчатое колесо – якорь тягового двигателя В соответствии с таблицей 3.6 запишем исходные данные: Вариант №14 (РА-1) 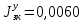 т*м2 т*м2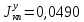 т*м2 т*м2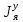 = 0,0032 т*м2 = 0,0032 т*м2 = 460 кН/м = 460 кН/м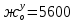 кН/м кН/мНа рис.1.1 приведены следующие обозначения: 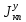 – момент инерции колесной пары относительно оси у, т*м2 – момент инерции колесной пары относительно оси у, т*м2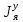 – момент инерции якоря тэд относительно оси у, т*м2 – момент инерции якоря тэд относительно оси у, т*м2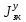 – момент инерции зубчатого колеса относительно оси у, т*м2 – момент инерции зубчатого колеса относительно оси у, т*м2 – угловая жесткость муфты , кН*м/рад – угловая жесткость муфты , кН*м/рад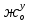 – угловая жесткость оси колесной пары, кН*м/рад – угловая жесткость оси колесной пары, кН*м/рад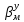 – коэффициент затухания муфты при ее угловой деформации, кН*с*м/рад – коэффициент затухания муфты при ее угловой деформации, кН*с*м/рад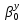 – коэффициент затухания оси колесной пары при ее угловой деформации, кН*с*м/рад – коэффициент затухания оси колесной пары при ее угловой деформации, кН*с*м/рад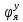 – координата углового колебания якоря, рад – координата углового колебания якоря, рад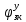 – координата углового колебания зубчатого колеса, рад – координата углового колебания зубчатого колеса, рад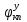 – координата угловых колебаний колесной пары, рад – координата угловых колебаний колесной пары, рад |
