Динамика систем
 Скачать 2.39 Mb. Скачать 2.39 Mb.
|
1.1 Определение величин коэффициентов затуханияОпределим коэффициенты затухания гасителей колебаний для схемы 3.6: n=0,05 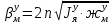 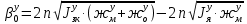 Кинематическая схема на рис.1.1.1 имеет три обобщённые координаты: q1= 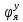 ; q2 = ; q2 = 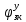 ; q3= ; q3= 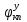 Значит составим 3 уравнения колебания. Для этого составим схему сил для рис.1.1: 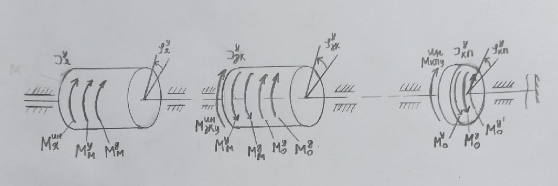 Рисунок 1.2. Силовая схема исследуемой модели Модули моментов сил инерции: 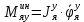 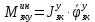 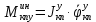 Моменты упругих и диссипативных сил: 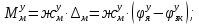 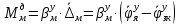 ; ;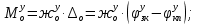 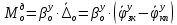 ; ;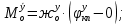 Запишем уравнение крутильных колебаний якоря зубчатого колеса и колесной пары. Так как система находится в равновесии, то сумма моментов всех сил равна 0. Уравнения крутильных колебаний якоря: 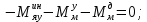 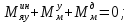 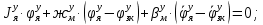 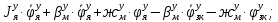 Уравнения колебаний зубчатого колеса: 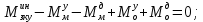 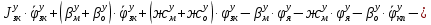 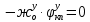 Уравнения крутильных колебаний колесной пары: 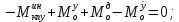 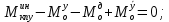 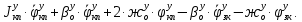 Сведем все уравнения в систему: 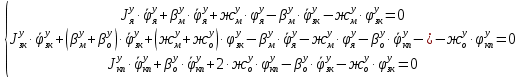 Приведение системы уравнений к форме Коши и понижение порядка системыПриведем полученную систему уравнений к форме Коши. Введем обозначения коэффициентов этой системы уравнений. Для начала оставим член со второй производной в левой части уравнений, а все остальные перенесем в правую часть и разделим правую часть дифференциальных уравнений на коэффициент при второй производной: Уравнение крутильных колебаний якоря: 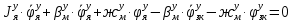 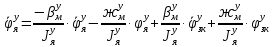 Введём обозначение коэффициентов: 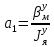 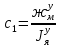 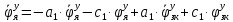 Уравнение крутильных колебаний зубчатого колеса: 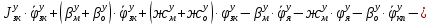 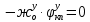 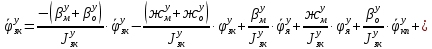 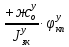 Введём обозначение коэффициентов: 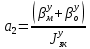 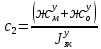 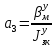 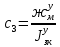 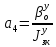 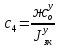 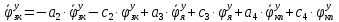 Уравнение крутильных колебаний колесной пары: 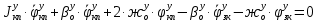 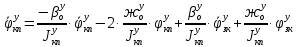 Введём обозначение коэффициентов: 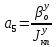 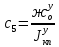 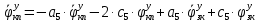 Понизим порядок системы уравнений, введя новое обозначение: 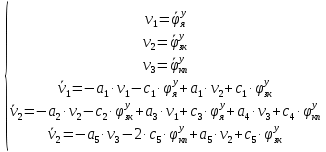 Парциальные частоты колебаний тележки: 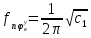 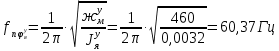 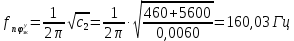 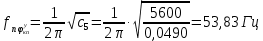 3. Исследование свободных колебаний модели путём решения системы ДУ методом Рунге-Кутта IV порядка в пакете Mathcad. Исследование свободных колебаний заданной системы производим в пакете Mathcad путём интегрирования полученной системы ДУ во временной области методом Рунге-Кутта 4 порядка. Для решения системы дифференциальных уравнений необходимо задаться временем расчета tk, длинной реализации N и по ним определить шаг расчета Δt. Время расчета обычно определяется в зависимости от меньшей частоты процесса колебаний 𝒇𝒎𝒊𝒏. В нашей схеме частот колебаний три. Меньшей является собственная частота крутильных колебани йколесной пары, которую в первом приближении можно принять равной парциальной частоте: 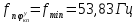 Период колебаний будет равен: 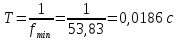 Обычно время расчета принимают равным: 𝑡𝑘 = 5 ∙ Т = 5 ∙ 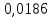 = 0,093 с = 0,093 с Длину реализации – N = 4096 точек = 212 точек Тогда 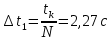 Для исследования задаем начальные условия на 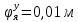 Графики этих зависимостей приведены на рисунках 3.1-3.9 (расположены на последующих страницах). Программа расчета колебаний и все результаты расчетов приведены в Приложении А.  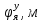 Начальные условия: 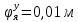      T1 T2 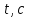 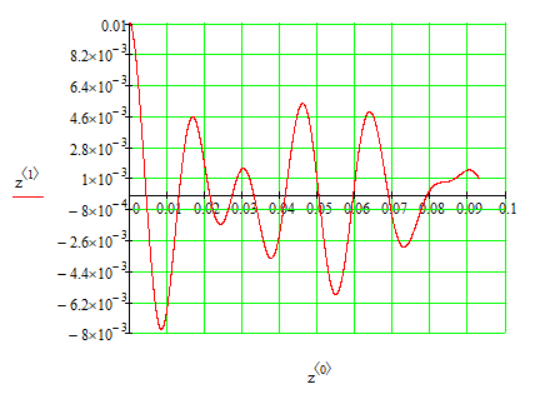 Рис.3.1. График зависимости крутильных колебаний якоря от времени Начальная амплитуда равна 0.01. Т1 = 0,0155 с, тогда f1 =64,51 Гц Т2=0,0195 с, тогда f2=51,28  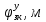      T1 T2   Рис.3.2. График зависимости крутильных колебаний зубчатого колеса от времени Начальная амплитуда равна 0.0012. Т1=0,008 с, тогда f1 =125 Гц. Т2=0,022, тогда f =45,45Гц       T2 T1 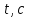 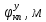 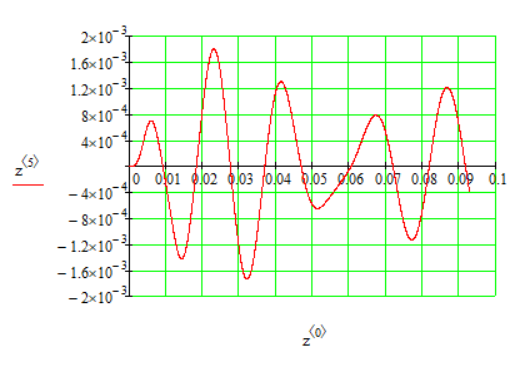 Рис.3.3. График зависимости крутильных колебаний колесной пары от времени Начальная амплитуда равна 0.00032. Т1 = 0,018 с, тогда f1 = 55,55 Гц Т2 = 0,028 с, тогда f2 = 35,71 Гц  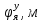 Начальные условия: 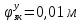      T1 T2  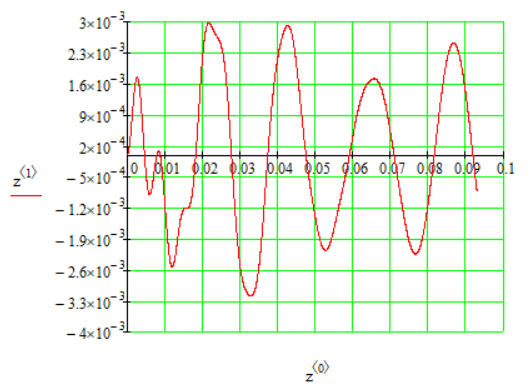 Рис.3.4. График зависимости крутильных колебаний якоря от времени Начальная амплитуда равна 0.00174. Т1 = 0,0085 с, тогда f1 = 117,65 Гц Т2 =0,022 с, тогда f2 = 45,45Гц       T2 T1   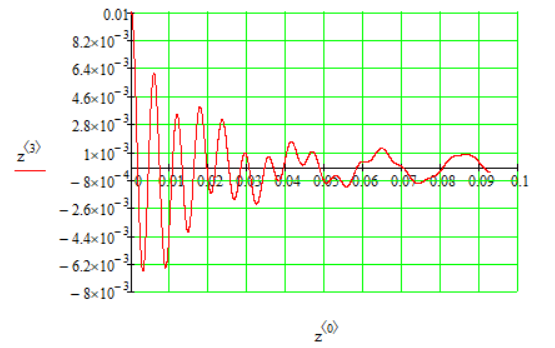 Рис.3.5. График зависимости крутильных колебаний зубчатого колеса от времени Начальная амплитуда равна 0.001. Т1 = 0,006 с, тогда f1 = 166,66 Гц Т2 = 0,0185 с, тогда f2 = 54,05 Гц  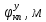      T2 T1 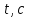 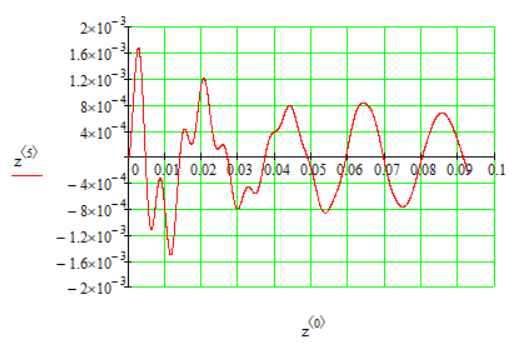 Рис.3.6. График зависимости крутильных колебаний колесной пары от времени Начальная амплитуда равна 0.00168. Т1 = 0,009 с, тогда f1 = 111,1 Гц Т2 = 0,02 с, тогда f2 = 50 Гц  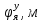 Начальные условия: 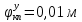      T2 T1 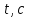 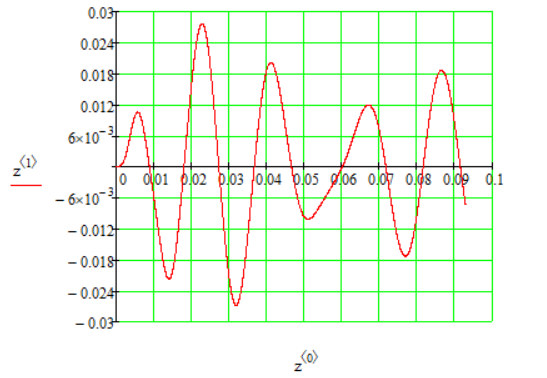 Рис.3.7. График зависимости крутильных колебаний якоря от времени Начальная амплитуда равна 0.01. Т1 = 0,0175 с, тогда f1 = 57,14 Гц Т2 = 0,022 с, тогда f2 = 45,45 Гц        T1 T2  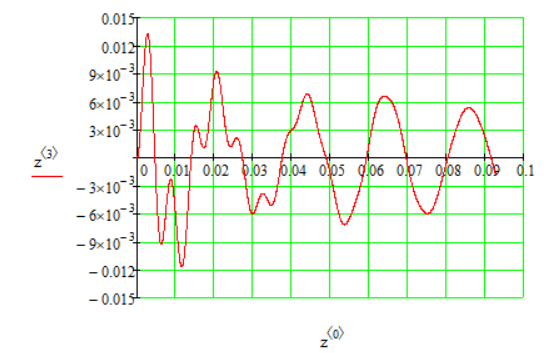 Рис.3.8. График зависимости крутильных колебаний зубчатого колеса от времени Начальная амплитуда равна 0.00168. Т1 = 0,009 с, тогда f1 = 111,11 Гц Т2 = 0,02 с, тогда f2 = 50 Гц       T2 T1  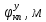 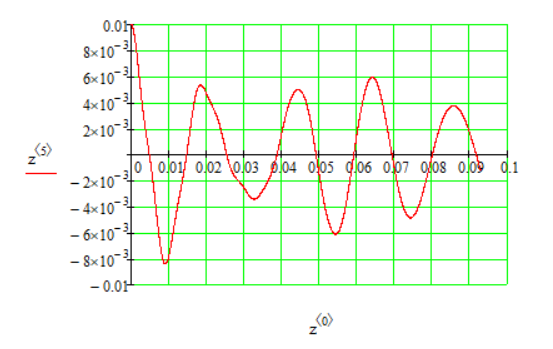 Рис.3.9. График зависимости крутильных колебаний колесной пары от времени Начальная амплитуда равна 0.01. Т1 = 0,0235 с, тогда f1 = 42,55 Гц Т2 = 0,02 с, тогда f2 = 50 Гц На графиках с заданными начальными условиями, собственные частоты колебаний схожи с парциальными частотами якоря, зубчатого колеса и колесной пары. Это значит, что графики построены верно. |
