Диплом 2010 по математике Математика 57 pag

• Название: Диплом 2010 по математике Математика 57 pag
• Дата: 06.04.2022
• Размер: 3.48 Mb.
• Имя файла: docsity-zhivaya-geometriya.docx
• Тип: Диплом; #447844
• страница: 3 из 7

1.3 Сущность геометрических построений

Развитие статических и динамических представлений детей относятся к числу важнейших задач обучения в школе. Сознавая это, учитель старается использовать богатые возможности курса черчения для постановки и решения различных пространственных задач в процессе графической подготовки учащихся. Немаловажную роль в расширении и продуктивном развитии пространственных представлений играют геометрические построения [8;12].

Деление окружности на равные части, достаточно распространенное геометрическое построение, основывается на законах симметрии, а именно является примером поворотной симметрии [1;7].

Деление окружности на восемь равных частей.

Деление окружности на восемь равных частей производится в следующей последовательности (рис.8):

Проводят две перпендикулярные оси, которые пересекая окружность в точках 1, 2, 3, 4 делят ее на четыре равные части;



Рисунок 8. Деление окружности на восемь равных частей.

Применяя известный прием деления прямого угла на две равные части при помощи циркуля или угольника строят биссектрисы прямых углов, которые, пересекаясь с окружностью в точках 5, 6, 7, и 8 делят каждую четвертую часть окружности пополам.

Деление окружности на три, шесть и двенадцать равных частей.

Деление окружности на три, шесть и двенадцать равных частей выполняется в следующей последовательности (рис.9):

Выбираем в качестве точки 1, точку пересечения осевой линии с окружностью.



Рисунок 9. Деление окружности на равные части, число которых кратно трем.

Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3; Точки 1, 2 и 3 делят окружность на три равные части;

Из точки 1 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 5 и 6;

Точки 1 - 6 делят окружность на шесть равных частей;

Дуги радиусом R, проведенные из точек 7 и 8 пересекут окружность в точках 9, 10, 11 и 12;

Точки 1 - 12 делят окружность на двенадцать равных частей.

Деление окружности на пять равных частей.

Деление окружности на пять равных частей выполняется в следующей последовательности (рис.10):

Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В; Из точки В опускают перпендикуляр на горизонтальную осевую линию;



Рисунок 10. Деление окружности на пять равных частей.

Из основания перпендикуляра - точки С, радиусом равным С1, проводят дугу окружности, которая пересечет горизонтальную осевую линию в точке D;

Из точки 1 радиусом равным D1, проводят дугу до пересечения с окружностью в точке 2, дуга 12 равна 1/5 длины окружности;

Точки 3, 4 и 5 находят откладывая циркулем по данной окружности хорды, равные D1.

Деление окружности на семь равных частей.

Деление окружности на семь равных частей выполняется в следующей последовательности (рис.11):

Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В; Из точки В опускают перпендикуляр на горизонтальную осевую линию;

Длину перпендикуляра ВС откладывают от точки 1 по окружности семь раз и получают искомые точки 1 - 7.



Рисунок 11. Деление окружности на семь равных частей.

Деление окружности на любое количество равных частей [23]

Для деления окружности на любое количество равных частей можно воспользоваться коэффициентами (см. таблицу 1.). Зная, на какое число n следует разделить окружность, находят коэффициент k. При умножении коэффициента k на диаметр D этой окружности, получают длину хорды, которую циркулем откладывают на заданной окружности n раз.

Таблица 1.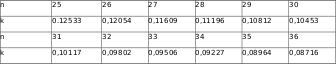



Циклоида - траектория (путь) точка А, лежащая на окружности, которая катится без скольжения по прямой АА12 (рис.12).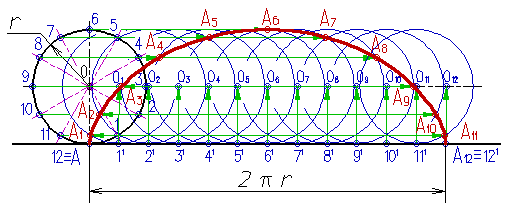



Рисунок 12. Циклоида.

Построение циклоиды производится в следующей последовательности

[12]:

На направляющей горизонтальной прямой откладывают отрезок АА12, равный длине производящей окружности радиуса r, (2pr); Строят производящую окружность радиуса r, так чтобы направляющая прямая была касательной к неё в точке А; Окружность и отрезок АА12 делят на несколько равных частей, например на 12; Из точек делений 11, 21, ...121 восстанавливают перпендикуляры до пересечения с продолжением горизонтальной оси окружности в точках 01, 02, ...012; Из точек деления окружности 1, 2, ...12 проводят горизонтальные прямые, на которых делают засечки дугами окружности радиуса r; Полученные точки А1, А2, ...А12 принадлежат циклоиде.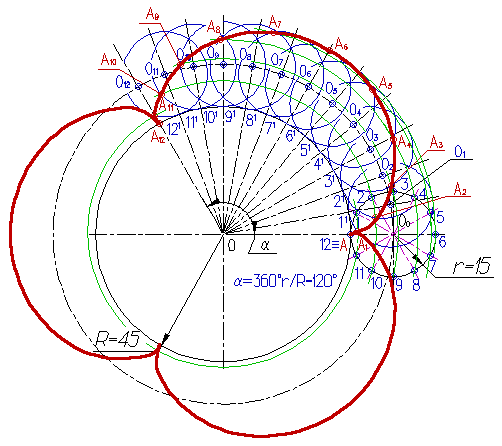



Рисунок 13. Эпициклоида.

Эпициклоида - траектория точки А, лежащей на окружности диаметра

D, которая катится без скольжения по направляющей окружности радиуса R (касание внешнее) (рис. 13).

Построение эпициклоиды выполняется в следующей последовательности [12]:

Производящую окружность радиуса r и направляющую окружность радиуса R проводят так, чтобы они касались в точке А; Производящую окружность делят на 12 равных частей, получают точки 1, 2, ... 12; Из центра 0 проводят вспомогательную дугу радиусом равным 000=R+r; Центральный угол a определяют по формуле a =360r/R. Делят дугу направляющей окружности, ограниченную углом a, на 12 равных частей, получают точки 11, 21, ...121; Из центра 0 через точки 11, 21, ...121 проводят прямые до пересечения с вспомогательной дугой в точках 01, 02, ...012;

Из центра 0 проводят вспомогательные дуги через точки деления 1, 2, ... 12 производящей окружности; Из точек 01, 02, ...012, как из центров, проводят окружности радиуса r до пересечения с вспомогательными дугами в точках А1, А2, ... А12, которые принадлежат эпициклоиде.

Гипоциклоида (рис.14) - траектория точки А, лежащей на окружности диаметра D, которая катится без скольжения по направляющей окружности радиуса R (касание внутреннее).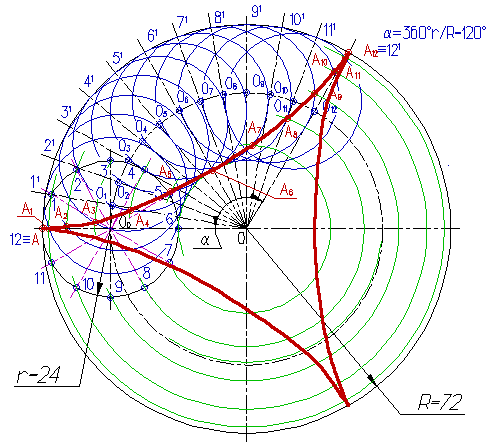

Рисунок 14. Гипоциклоида.

Построение гипоциклоиды выполняется в следующей последовательности [12]:

Производящую окружность радиуса r и направляющую окружность радиуса R проводят так, чтобы они касались в точке А; Производящую окружность делят на 12 равных частей, получают точки 1, 2, ... 12; Из центра 0 проводят вспомогательную дугу радиусом равным 000=R-r; Центральный угол a определяют по формуле a =360r/R. Делят дугу направляющей окружности, ограниченную углом a, на 12 равных частей, получают точки 11, 21, ...121; Из центра 0 через точки 11, 21, ...121 проводят прямые до пересечения с вспомогательной дугой в точках 01, 02, ...012; Из центра 0 проводят вспомогательные дуги через точки деления 1, 2, ... 12 производящей окружности; Из точек 01, 02, ...012, как из центров, проводят окружности радиуса r до пересечения с вспомогательными дугами в точках А1, А2, ... А12, которые принадлежат гипоциклоиде.

Спираль Архимеда (рис.15) - плоская кривая, которую описывает точка, движущаяся равномерно-поступательно от центра 0 по равномерновращающемуся радиусу.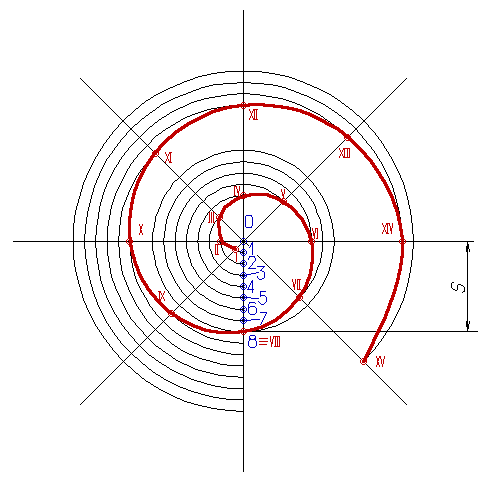



Рисунок 15. Построение спирали Архимеда.

Построение архимедовой спирали заданным шагом S - расстояние от центра 0 до точки VIII, выполняется в следующей последовательности [12]:

Из центра 0 проводят окружность радиусом, равным шагу S спирали и делят шаг и окружность на несколько равных частей Точки деления нумеруют;

Из центра 0 радиусами 01, 02, 03, ... проводят дуги до пересечения с соответствующими радиусами в точках I, II, III, ...; Полученные точки принадлежат спирали Архимеда с заданным шагом S и центром 0.

ГЛАВА 2. ИЗ ИСТОРИИ