Диплом 2010 по математике Математика 57 pag

• Название: Диплом 2010 по математике Математика 57 pag
• Дата: 06.04.2022
• Размер: 3.48 Mb.
• Имя файла: docsity-zhivaya-geometriya.docx
• Тип: Диплом; #447844
• страница: 7 из 7

3.2 Выбор практических заданий

Предлагаемые практические задания предназначены для обучения учащихся геометрическим построениям на плоских поверхностях в курсе технической графики и дизайна [2;4;6;13;14;18;22;24;26].

На основе общего содержания программы «Черчение» для средней школы разработаны задания, которые делятся на следующие разделы:

1. 
   Деление окружности на равные части;
   
2. 
   Сопряжение двух прямых; 3. Спиралевидные закономерности;
   

4. Циклические закономерности.

Внутри каждого из этих разделов предполагается деление на подразделы:

1. 
   Определение содержания геометрических построений и их применение в различных областях;
   
2. 
   Определение методов построения изображения.
   

При выполнении этого изображения у ребенка соединяется образовательная подготовка с творческой.

Опираясь на знания детей, учитывая их возрастные особенности и технические возможности, учитель должен в доступной форме донести до учащихся смысл задания, придерживаясь в получении знаний и умений принцип построения от легкого к трудному, от простого к сложному.

В чем состоит смысл предлагаемых заданий? В том, чтобы объяснить детям сущность геометрических построений, применяемых в той или иной области декоративного искусства, архитектуры, на примере природных явлений.

Предлагаемые интегрированные задания позволяют развить творческие способности и технические навыки на основе имеющихся знаний, получая при этом новый результат. Интегрированные задания очень эффективны на итоговых занятиях по теме, где можно проверить возможности применения знаний, приобретенных на одном предмете (например, геометрии или биологии) в творческих заданиях по другому предмету (например, черчении). Такие задания проверяют возможности ребенка и будут развивать его творческий потенциал [18].

3.4 Содержание практической работы

Практическая часть нашей работы представлена пятью заданиями.

Лист 1. Паук.

На листе представлена половина изображения паука и половина чертежа паука. Для соединения этих двух изображений использован принцип билатеральной симметрии.

По имеющемуся изображению (рисунку, фотографии) учащиеся должны выделить виды геометрических построений, присутствующих у данного организма. Так как паук имеет восемь лап, то ведущим построением будет деление окружности на 8 равных частей.

Лист 2. Подсолнух.

На листе представлена половина изображения цветка и половина его чертежа.

По имеющемуся изображению (рисунку, фотографии) учащиеся должны выделить виды геометрических построений, присутствующих у этого цветка.

В результате исследований было установлено, что семена подсолнуха расположены в цветке по принципу спирали Архимеда. А чтобы построить лепестки, надо разделить окружность на равные части. Значит, чертеж будет содержать два вида геометрических построений: деление окружности на 12 (в нашем случае) равных частей, и построение спирали Архимеда.

Лист 3. Морская звезда.

На листе представлена половина изображения морской звезды и половина ее чертежа.

По имеющемуся изображению (рисунку, фотографии) учащиеся должны выделить виды геометрических построений, присутствующих у этого морского организма.

Рассмотрев фотографию морской звезды, мы видим, что она имеет пять лучей. Значит построение чертежа будет основано на делении окружности на пять равных частей. Кроме того, морская звезда имеет плавные переходы между лучами, поэтому мы будем использовать сопряжение двух прямых. Также, следует отметить, что лучи морской звезды расположены по принципу поворотной симметрии пятого порядка, которая встречается в живой природе очень редко.

Лист 4. Ракушка.

На листе представлена половина изображения раковины моллюска и половина чертежа его раковины.

По имеющемуся изображению (рисунку, фотографии) учащиеся должны выделить виды геометрических построений, присутствующих у раковины моллюска.

Рассмотрев раковину моллюска типа Наутилус, можно с уверенностью сказать, что она имеет спиральную зависимость. Значит чертеж раковины будет выполнен на основе спирали Архимеда.

Лист 5. Орхидея.

На листе представлена половина изображения цветка и половина его чертежа.

По имеющемуся изображению (рисунку, фотографии) учащиеся должны выделить виды геометрических построений, присутствующих у этого цветка.

Цветок имеет ярко выраженную циклическую закономерность, поэтому чертеж выполняется на основе эпициклоиды. Сложность данного задания состоит в том, что в общем курсе черчения и графики построение эпициклоиды не рассматривается.

Заключение

Графические средства отображения информации широко используются во всех сферах жизни общества. Графические изображения характеризуются образностью, символичностью, компактностью, относительной легкостью прочтения. Именно эти качества графических изображений обусловливают их расширенное использование. Прогнозируется, что около 60—70% информации будет иметь графическую форму предъявления. Учитывая мировую тенденцию развития, общее среднее образование должно предусмотреть формирование знаний о методах графического предъявления и восприятия информации, что обеспечит условия и возможность ориентации социума в обществе [28].

Реализация принципа культуросообразности содержания общего среднего образования невозможна без ознакомления школьников с огромным пластом графической культуры. За многовековую историю в ее недрах был выработан графический язык делового общения. Изучение графического языка как синтетического, имеющего свою семантическую основу, является необходимым, поскольку он общепризнан в качестве международного языка общения. Знание его может стать одной из преимущественных характеристик для получения работы, а также продолжения образования.

Большое значение графический язык приобретает в рамках национальной доктрины образования Российской Федерации, стратегические цели которого тесно связаны с задачами экономического развития страны и утверждением ее статуса как мировой державы в сфере культуры, науки, высоких технологий. Решить поставленные задачи невозможно, если школьное образование не обеспечит должный уровень графической подготовки ее выпускников.

Предмет «Черчение» наиболее эффективно и целенаправленно развивает наглядно-образное мышление, имеющее очень важное место в любом творческом процессе, поскольку новое решение предстает перед мысленным взором в виде картин, схем, моделей.

Кроме того, в процессе овладения данной дисциплиной совершенствуется репродуктивное и продуктивное воображение, проявляющееся в создании объемных образов реального мира и построении новых (конструирование, переконструирование, совершенствование, преобразование и т. д.). Перечисленные интеллектуальные операции, задействованные в названных процессах, носят универсальный характер и могут быть применены в других формах и видах деятельности. Этот предмет способствует созданию пространственных представлений большей или меньшей степени обобщенности и схематичности. Развитие пространственных представлений позволяет сформировать у школьников эффективные способы переработки информации — визуализации, что способствует огромной экономии времени. При таком способе работы информация практически одномоментно трансформируется в некоторую обобщенную модель, содержащую необходимые и достаточные элементы для понимания формы, ситуации, явления и др. Данный учебный предмет активно развивает сенсорные способности человека [28].

Сказанное позволяет увидеть уникальность и универсальность учебной дисциплины для развития познавательных способностей человека, расширения круга используемых мыслительных средств и умственных операций, что, в свою очередь, повышает адаптивные возможности человека.

Все перечисленное показывает необходимость рассматривать графическое образование как необходимую составляющую содержания общего образования, отвечающую принципам гуманизации, гуманитаризации, культуросообразности, обеспечивающих коммуникативное и технологическое образование учащихся.

Исходя из вышесказанного, можно сделать следующие выводы:

1. 
   Использование интегрированных заданий в курсе «Черчение» положительно влияет на мотивацию школьников к учебным предметам, способствует лучшему усвоению знаний, и более качественному формированию умений и навыков геометрических построений.
   
2. 
   Геометрические построения являются интегрированными умениями, необходимыми в различных школьных предметах.
   
3. 
   Формирование навыков геометрических построений способствует развитию наглядно-образного мышления, репродуктивного и продуктивного воображения, пространственных представлений, а значит способности эффективной обработки информации.
   

Данная работа может применяться на уроках черчения (с использование компьютерной техники), а также на факультативных и пропедевтических курсах по технической графике, основам дизайна и т.д.

В дальнейшем, работа над этой темой может быть продолжена. Можно разработать учебно-методический комплект для факультативных занятий учащихся 7-х классов, в основу заданий которого будет положен принцип геометрических построений.

Литература

1. 
   Атанасян Л.С., Базылев В.Т. Геометрия. Часть первая. М.:
   

Просвещение, 1986. – 268 с.

2. 
   Аргунов Б.М., Балк М.Б. Элементарная геометрия. М.: Просвещение,
   

1986. – 422 с.

3. 
   Бахман Ф.М. Построение геометрии на основе понятия симметрии. М.: Просвещение, 1969. – 356 с.
   
4. 
   Беккер Б.М., Некрасов В.Б. Применение векторов к решению задач. СПб.: Питер, 1997. – 188 с.
   
5. 
   Беляев М.И. Природные механизмы законов сохранения. Симметрия и асимметрия. М.: Наука, 2007. -126 с
   
6. 
   Берман Г.Н. Циклоида. Об одной замечательной кривой линии и некоторых других, с ней связанных. 3-е изд. М.: Наука, 1980. – 112 с.
   
7. 
   Боголюбов С.К. Задания по курсу черчения (в двух книгах): Учеб. пособие для техникумов. – Книга первая: Основы черчения и начертательной геометрии. М.: Высш. школа, 1978. – 168 с.
   
8. 
   Ботвинников А.Д. Об актуальных вопросах методики обучения черчению. Пособие для учителя. М.: Просвещение, 1977. – 191 с.: ил.
   
9. 
   Вигнер Ю. Симметрия и законы сохранения. М.: Наука, 1963. – 122 с.
   
10. 
    Вигнер Ю. Роль принципов инвариантности в натуральной философии.
    

М.: Наука, 1964. – 162 с.

3. 
   Виленкин Н.Я. Функции в природе и технике: Кн. для внеклас. чтения IX-X кл. – 2-е изд., испр. – М.: Просвещение, 1985. – 192 с. – (Мир знаний). 12. Вольхин К.А.. Астахова Т.А. Геометрические основы построения чертежа. Геометрическое черчение. Электронное учебное пособие. Новосибирск, 2004
   

13. 
    Воротников И.А. Занимательное черчение. 2-е изд., доп. М.:
    

Просвещение, 1969. – 149 с.: ил.

13. 
    Гервер В.А. Творчество на уроках черчения: Книга для учителя. – М.: Гуманит. изд. Центр ВЛАДОС, 1998. – 144 с.: ил.
    
14. 
    Глейзер Г.И. История математики в школе: IX-X кл. Пособие для учителей. – М.: Просвещение, 1983. – 351 с.: ил.
    
15. 
    Дадаян А.А. Основы черчения и инженерной графики. Геометрические построения на плоскости и в пространстве. М.: Изд-во Форум, 2007. – 464 с.:
    

ил.

13. 
    Емельянов А.Е. Универсальная геометрия в природе и архитектуре. (Симметрия, гармония, абсолютные системы отсчета). Донбасс, 1990.
    
14. 
    Козлова Н.В. Принцип интегрирования в обучении черчению учащихся 7-го класса. Методические рекомендации для учителей черчения и студентов художественно-графического факультета педагогического института. Нижний Тагил: НТГПИ, 1997. – 40 с.
    
15. 
    Мандельброт Бенуа. Фрактальная геометрия природы. М.: Институт компьютерных исследований, 2002. – 660 с.: ил.
    
16. 
    Маркушевич А.И. Замечательные кривые. М.: Наука, 1978. – 48 с.: ил.
    
17. 
    Монж Г. Начертательная геометрия./ Комментарии и редакция Д.И. Каргина.- М.: АН СССР, 1974. – 291 с.
    
18. 
    Пантуев А.В.. Виртуальные лаборатории и активизация работы школьников. Сб. Стимулирование познавательной деятельности студентов и школьников, М: МГПУ, 2002. С. 30-33.
    
19. 
    Покровский, В.Г. Геометрические построения на плоскости: учебное пособие / В.Г. Покровский – М.: МЦНМО, 2002.– 98 с.
    
20. 
    Потоцкий М.В. Что изучает проективная геометрия? М.: Просвещение, 1982. – 342 с.
    
21. 
    Пидоу Д. Геометрия и искусство. Пер. с англ. Ю.А. Данилова под ред. и с предисл. И.М. Яглома. – М.: Мир, 1979. – 332 с.: ил. (В мире науки и техники).
    
22. 
    Репникова Г.Г. Геометрические преобразования пространства.
    

Ставрополь, 1992. – 168 с.

13. 
    Сонин А.С. Постижение совершенства. М.: Высш. школа, 1987. – 324 с.
    
14. 
    Степакова В.В. Методическое пособие по черчению. Графические работы: Книга для учителя/ В.В. Степакова. – М.: Просвещение, 2001. – 93 с.: ил.
    
15. 
    Тарасов Л.В. Симметрия в окружающем мире/Л.В. Тарасов. – М.: ООО «Издательский дом «ОНИКС 21 век!»: ООО «Издательство «Мир и
    

Образование», 2005. – 256 с.: ил.

13. 
    Узоры симметрии /Под ред. М. Сенешаль, Дж. Флека. М.: Наука, 1977. – 254 с.
    
14. 
    Цейтен Г.Г. История математики в древности и средние века. ГТТИ, 1932. – 402 с.
    
15. 
    Шарыгин И.А., Ерганжиева Л.Н. Наглядная геометрия. М.:
    

Просвещение, 1995. – 378 с.

13. 
    Шафрановский И.И. Симметрия в природе. – 2-е изд., перераб. – Л.:
    

Недра, 1985. – 168 с.: ил.

Практическая часть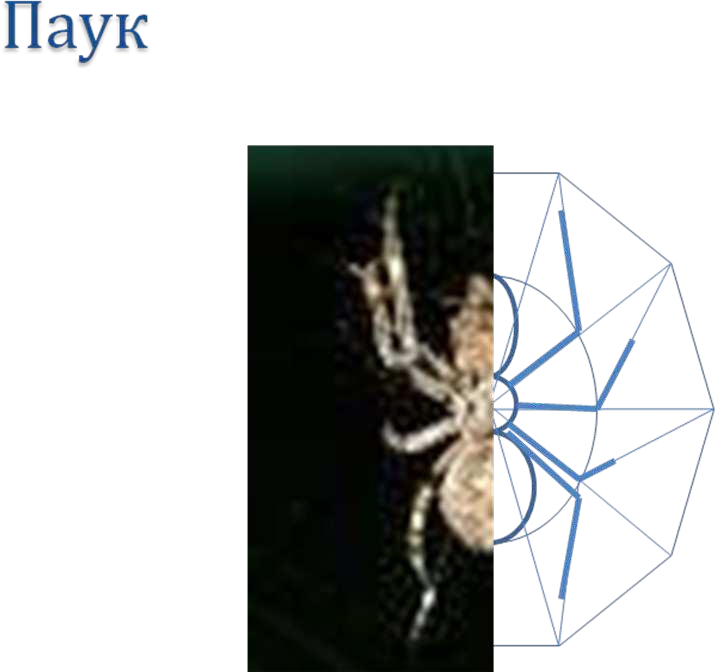

Downloaded by: Alexxx05 ([e-mail])