Диплом 2010 по математике Математика 57 pag
 Скачать 3.48 Mb. Скачать 3.48 Mb.
|
2.2 Открытие некоторых геометрических построений"Золотым веком" греческой геометрии называют эпоху, когда жили и творили математики Архимед (287-195 гг. до н.э.), Эрастофен (275-195гг. до н.э.), Аполлоний Пергский (250-190гг. до н.э.). Измерение криволинейных образов связано с именем Архимеда. Он указал методы измерения длины окружности, площади круга, сегмента параболы и спирали, объемов и поверхностей шара, других тел вращения и др [31]. К началу XVII века математики знали такие кривые линии, как эллипс, гиперболу, параболу и т.д. однако в то время еще не было общего метода изучения линий, и потому исследование каждой кривой превращалось в сложную научную работу. Открытия Декарта и Ферма доли в руки математиков метод для получения и изучения новых кривых – надо было написать уравнение кривой и сделать выводы, исследуя это уравнение. Сам Декарт в 1638 году придумал новую кривую, уравнение которой имеет вид x3+y3-3axy=0, a>0 (рис. 20). 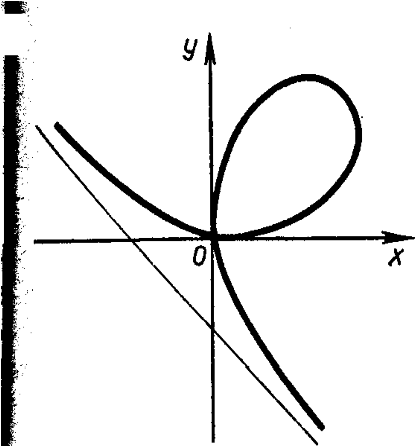 Рисунок 20. Декартов лист. Ее сейчас называют декартовым листом. Любопытно, что хотя Декарт применял уже в своей алгебре не только отрицательные, но даже мнимые числа, он не рассматривал отрицательных значений координат. Первоначально декартов лист считали симметричным относительно осей координат (рис. 21). 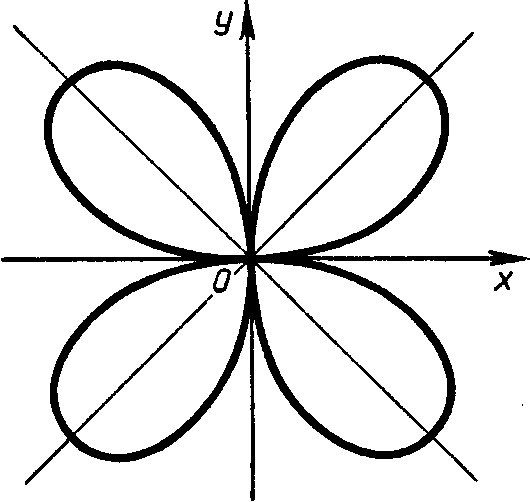 Рисунок 21. Симметричность Декартова листа. Окончательно форма кривой была установлена лишь через полстолетия Х.Гюйгенсом (1629-1695) и Иоганном Бернулли (1667-1748). Декартов лист, эллипс, гипербола, парабола являются алгебраическими кривыми. Так называют кривые, уравнение которых имеет вид Р (х,у)=0, где Р(х,у) – многочлен от х и у. но уже Галилей и Декарт изучали циклоиду – кривую, описываемую точкой обода колеса, катящегося без скольжения по прямой дороге. Можно доказать, что уравнение одной арки циклоиды имеет вид x=r arcos * (r-y)/r - √2ry-y2. Так как в это уравнение входит обратная тригонометрическая функция, циклоида не является алгебраической кривой. К неалгебраическим кривым нельзя было применять алгебраические методы, разработанные Декартом, поэтому их назвали трансцендентными кривыми (от латинского «трансценденс» - выходящий за пределы). Некоторые трансцендентные кривые были известны еще древнегреческим математикам. Например, в связи с задачей о спрямлении окружности (построении отрезка, длина которого равна длине этой окружности) Архимед построил особую спираль, определив ее на языке механики как траекторию точки, совершающей равномерное и поступательное движение по лучу, который в это же время равномерно вращается вокруг своего начала. После того, как были открыты логарифмы, стали изучать свойства графиков логарифмической и показательной зависимостей. Задачи механики требования отыскивания формы провисшего каната (так называемой цепной линии). Поиски кривой, длина дуги которой пропорциональна разности длин векторов, проведенных в ее концы, привели к открытию логарифмической спирали [11]. В течение XVII столетия было открыто больше кривых, чем за всю предшествующую историю математики, и понадобились общие понятия, которые позволили бы единым образом трактовать и изучать как алгебраические, так и трансцендентные кривые, как тригонометрические, так и логарифмические зависимости. Творцом ортогональных проекций и основоположником начертательной геометрии является французский геометр Гаспар Монж (1746-1818гг.). Знания, накопленные по теории и практике изображения пространственных предметов на плоскости, он систематизировал и обобщил, поднял начертательную геометрию на уровень научной дисциплины. "… Нужно научить пользоваться начертательной геометрией" - говорил Г. Монж [21]. В работе Г. Монжа "Начертательная геометрия" ("Geometric Descriptive"), изданной в 1798г., решались задачи: Применение теории геометрических преобразований. Рассмотрение некоторых вопросов теории проекций с числовымиотметками. Подробное исследование кривых линий и поверхностей, в частностиприменение вспомогательных плоскостей и сфер при построении линии пересечения поверхностей. Появление начертательной геометрии было вызвано возраставшими потребностями в теории изображений. Дальнейшее развитие начертательная геометрия получила в трудах многих ученых [21;32]. Глава 3. Практическая часть |
