!Конспект лекций Теоретичекая и прикладная механика. Лекция 1 Предмет теоретической механики. Кинематика точки

• Название: Лекция 1 Предмет теоретической механики. Кинематика точки
• Дата: 17.10.2022
• Размер: 3.52 Mb.
• Имя файла: !Конспект лекций Теоретичекая и прикладная механика.doc
• Тип: Лекция; #738124
• страница: 1 из 10

Лекция 1 –«Предмет теоретической механики. Кинематика точки»

Цель лекции – показать место курса теоретической механики в учебном процессе и ее связь с другими дисциплинами, изучаемыми в ВУЗе; изложить кинематику точки.

План лекции

1. 
   История развития теоретической механики
   
2. 
   Введение в кинематику. Основная задача кинематики. Кинематика точки
   
3. 
   Векторный способ задания движения точки
   
4. 
   Координатный способ задания движения точки в декартовых координатах
   
5. 
   Естественный способ задания движения точки
   

КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ

Рассмотрим историю науки применительно к теоретической механике. Раскроем смысл самого понятия «теоретическая механика». Название это наука получила от греческого слова «машина». В связи с этим, вплоть до начала 19 века механика определялась как наука о машинах. В общем комплексе наук о машинах механика, которая называется теперь теоретической, занимает первое место. Она изучает общие свойства машин, которые характеризуют все действующие машины, независимо от их специального назначения. В каждой работающей машине имеются движущие ее части – так называемые детали, причем они давят друг друга, толкают и вообще производят некоторые силовые воздействия. Таким образом, общими свойствами машин являются движение и сила; теоретическую механику можно было бы определить как науку о движениях и силах. В связи с этим определением появилось и деление теоретической механики на СТАТИКУ, которая рассматривает силы сами по себе, когда они не производят движения, т.е. находятся в равновесии, КИНЕМАТИКУ, которая изучает движение, без учета сил и ДИНАМИКУ, в которой исследуются оба основных элемента работы – движение и сила в их взаимодействии.

Теоретическая механика определяется как наука о механическом движении. Тело движется, если оно с течением времени изменяет свое положение относительно некоторой системы отсчета.

В этом определении подчеркивается, во-первых, относительность движения и, во-вторых, элемент времени; этим механическое движение отличается от простого перемещения, рассматриваемого в геометрии без учета времени.

Кинематика делится на кинематику точки и кинематику твердого тела. В кинематике время t принимается за независимое переменное, а все другие кинематические характеристики (расстояние, скорость, ускорение и т.п.) рассматриваются как функции времени.

Основной задачей кинематики является определение всех кинематических величин, характеризующих движение, как отдельной точки, так и тела в целом. Эта задача может быть решена путем применения различных способов кинематического задания движения точки.

Векторный способ задания движения точки. Движение точки можно задать, если выразить ее радиус-вектор в некоторой системе отсчета в виде функции времени

. (1)

Функция для определенности дальнейших рассуждений предполагается непрерывной, дважды дифференцируемой. Такое задание радиус-вектора точки предполагает наличие системы отсчета, но не конкретизирует ее. В данном случае траекторию точки можно определить как годограф ее радиус-вектора, т.е. геометрическое место концов радиус-вектора , изменяющегося во времени согласно зависимости (1).

Скорость точки при векторном способе задания движения есть векторная величина, равная первой производной по времени от радиус-вектора точки:

. (2)

Скорость всегда направлена по касательной к траектории в сторону движения точки, а ее численное значение определяется модулем 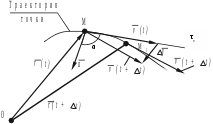. Единица измерения скорости в СИ – м/c.


Рис. 1

Ускорение точки по своему физическому смыслу есть изменение скорости, и определяется как первая производная по времени от скорости точки или как вторая производная от радиус-вектора точки:

(3)

Численное значение ускорения определяется модулем 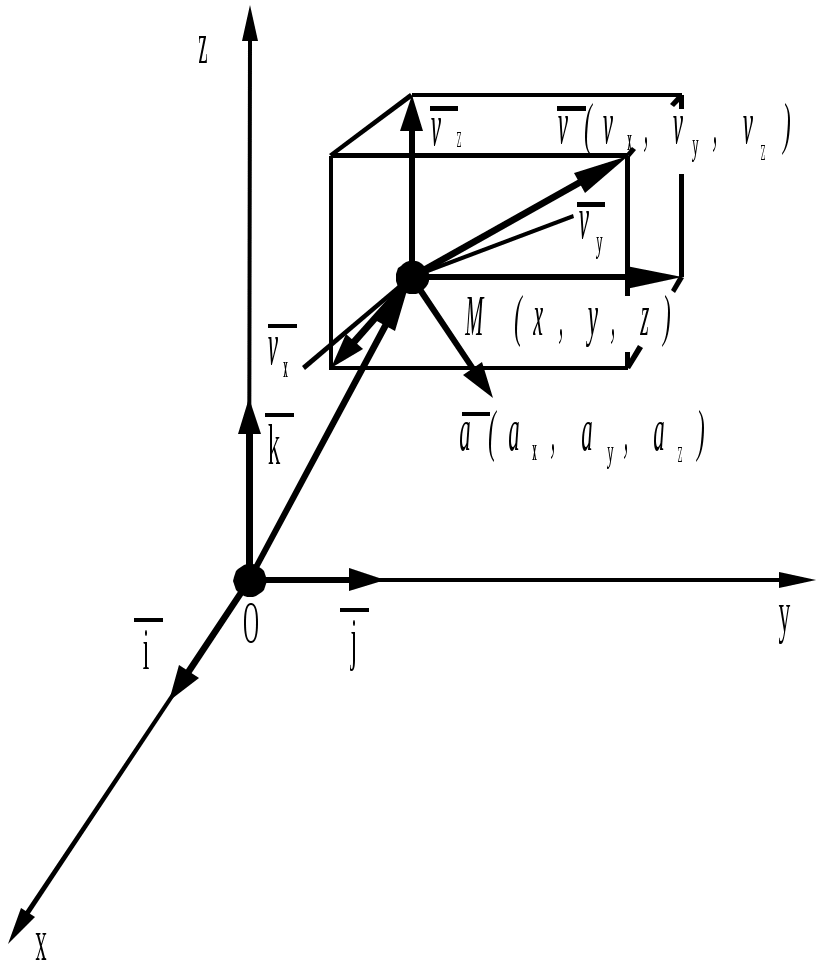; единица измерения ускорения в СИ – м/c².

Координатный способ задания движения точки. Прямоугольная декартова система координат с началом в точке О показана на рис.2. Положение точки М в пространстве с использованием данной системы координат задается ее координатами x,y,z. Чтобы знать положение точки в пространстве в любой момент времени необходимо иметь уравнения движения точки в виде

(4)

Эти выражения представляют собой уравнения движения точки в декартовой системе координат и одновременно являются уравнениями траектории точки, записанными в параметрической форме.


Рис. 2


Чтобы найти уравнение траектории в форме непосредственной зависимости между координатами x,y,z, из системы уравнений (4) необходимо исключить время.

С учетом уравнений (4) радиус-вектор точки М (см. рис. 2) будет иметь вид

. (5)

На основании (2) и (5), будем иметь

. (6)

Таким образом, в раасматриваемом случае скорость точки представляет собой сумму следующих векторов, параллельных ося декартовой системе координат:

, (7)

а ее численное значение (модуль) определится по формуле

(8)

Формула для расчета ускорения примет вид

, (9)

а численное значение ускорения будет равно модулю вектора :

(10)

Естественный способ задания движения точки. Если траектория точки известна, то зачки можно естественным способом. Для этого необходимо: зафиксировать на траектории точку начала отсчета, выбрать положительное и отрицательное направления движения и указать закон движения точки по траектории в виде

(11)

Всего этого в совокупности достаточно для однозначного определения положения точки в пространстве в любой момент времени (рис.3)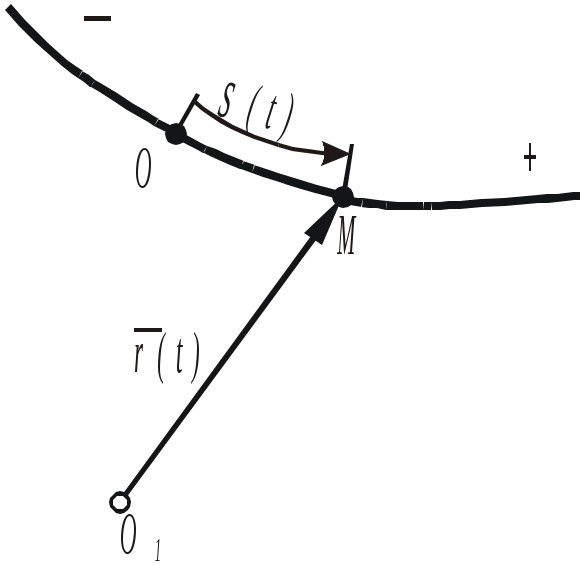


Рис. 3


Согласно основному определению скорости (1): или, с учетом определения единичного вектора ,

. (12)

Из (12) следует, что проекция скорости точки на ось, касательную к траектории точки, равна

.

Эту производную иногда называют алгебраической скоростью.

Для ускорения имеем

где .

Таким образом,

(13)

ил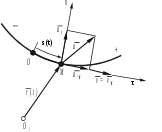и

. (14)

П оследние соотношения представляют собой сумму касательной и нормальной составляющих (рис.4): .

Проекции ускорения на оси естественной системы координат (касательную, нормаль и бинормаль) равны




Рис. 4




(15)
Очевидно, что и модуль ускорения

(16)

Характер движения точки по траектории можно определить, исходя из знака произведения скорости и ускорения: в случае - движение точки ускоренное, в случае - движение точки замедленное .При движение точки равномерное , в этом случае при движении по криволинейной траектории и .
ГЛОССАРИЙ

Теориялық механика	Теоретическая механика	Classical mechanics
Механикалық қозғалыс	Механическое движение	Mechanical motion
Материялық нүкте	Материальная точка	Particle
Санақ жүйе	Система отсчета	Frame of reference
Кинематика	Кинематика	Kinematics
Нүктенің траекториясы	Траектория точки	Trajectory of particle
Жылдамдық	Скорость	Velocity
Үдеу	Ускорение	Acceleration
Табиғи үшжақтық өстері	Оси естественного трехгранника	Axes of a natural trihedral
Жанама үдеу	Касательное ускорение	Tangential acceleration
Нормаль үдеу	Номальное ускорение	Normal acceleration

Домашнее залание - рассмотреть самостоятельно естественный трехгранник (оси естественной системы координат).
Cм. Курс теоретической механики (под ред. академика К.С.Колесникова ),

Москва, издательство МГТУ имени Н.Э.Баумана,2000- 62-64с.

Лекция 2. «Кинематика простейших движений твердого тела»
Цель лекции – рассмотреть простейшие движения твердого тела,установить кинематические характеристики всего тела, а затем изучить движение каждой из его точек в отдельности.
План лекции

1. 
   Кинематика твердого тела. Виды движения
   
2. 
   Поступательное движение твердого тела. Теорема о скоростях и ускорениях точек тела при поступательном движении
   
3. 
   Вращение тела вокруг неподвижной оси. Угловая скорость и угловое ускорение тела.
   
4. 
   Скорости и ускорения точек тела, вращающегося вокруг неподвижной оси.
   

КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ

Далеко не во всех задачах кинематики можно пренебрегать размерами движущегося тела и принимать его за точку. Для тех случаев, когда расстояния между частицами тела не изменяются, но по условиям задачи приходится учитывать движения его различных частиц, разработан раздел кинематики, называемый кинематикой твердого тела.

Если закрепить две точки твердого тела, то оно сможет поворачиваться вокруг прямой, проходящей через две эти точки. Если закрепить еще и третью точку, не лежащую на той же прямой, то тело окажется закрепленным. Таким образом, положение твердого тела определяется положением трех его точек, не лежащих на одной прямой, а движение тела – движением трех его точек.

Поступательным движением твердого тела называют такое движение, при котором любая прямая, взятая в теле, остается параллельной своему начальному направлению.

Свойства поступательного движения: 1) траектории всех точек тела, совершающего поступательное движение, конгруэнтны, т.е. одинаковы; 2) скорости всех точек тела одинаковы; 3) ускорения всех точек теда одинаковы.

Эти выводы можно подтвердить на основании следующего анализа. Для двух любых точек А и В тела, совершающего поступательное движение (рис.1), можно записать соотношение



где 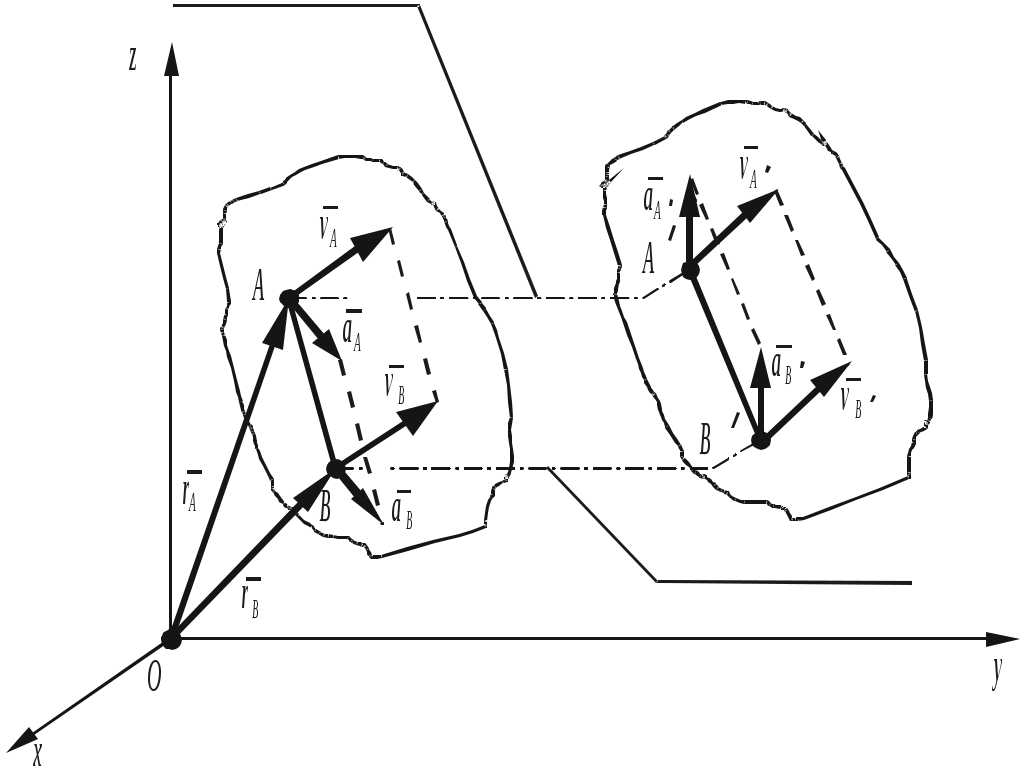- вектор, имеющий постояный модуль и направление во время движения (рис.1)



Рис.1

Дифференцируя левую и правую части приведенного выше векторного соотношения и учитывая, что , получаем или Дифференцируя по времени левую иправую части полученного соотношения для скоростей находим или

Вращением твердого тела вокруг неподвижной оси назывется такое движение тела , при котором в теле найдутся по крайней мере две точки, которые все время движения будут оставаться неподвижными. Прямая, проведенная через эти точки называется осью вращения твердого тела.

Вращательное движение твердого тела определено, если задан как функция времени угол, на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела:



где - непрерывная дважды дифференцируемая функция времени.

Алгебраическая угловая скорость вращения тела

.

Угловую скорость можно определить и как вектор, расположенный на оси вращения и равный , где - единичный вектор, задающий положительное направление оси вращения. Численное значение угловой скорости равно модулю вектора :

.

Единица измерения в СИ - рад/с.

Изменение угловой скорости тела во времени характеризуется угловым ускорением.

Алгебраическим угловым ускорением тела называется первая производная от алгебраической угловой скорости или вторая производная по времени от угла поворота вокруг неподвижной оси:

.

Как векторную величину угловое ускорение можно определить так:

.

Проекция углового ускорения на ось вращения

,

т.е. она равна алгебраическому угловому ускорению тела, если положительные направления отсчета угла и оси соответствуют правой декартовой системе координат. Значение (модуль) углового ускорения

.

Единица измерения углового ускорения в СИ - рад/с².

Векторы и являются скользящими векторами, расположеными на оси вращения тела. Вращательное движение называется ускоренным, если и замедленным, если , при тело вращается равномерно, в этом случае .


Скорость точки А определим в виде 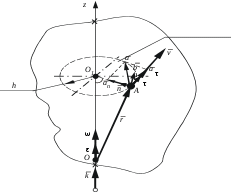(рис.2). В данном случае , так что поскольку , то В итоге получаем

,

которая называется векторной формулой Эйлера.

Модуль скорости точки определятся как Скорости точек при вращении вокруг неподвижной оси направлены по касательной к окружности радиусом в соответствии с направлением угловой скорости тела.

Ускорение точки А тела Здесь

следовательно

Рис.2

Слагаемые в правой части представляют собой касательную и нормальную составляющие ускорения точки.

Молуль касательного ускорения равен



Вектор всегда направлен по нормали к траектории точки в сторону ее вогнутости (к оси вращения тела). Модуль нормального ускорения точки



Полное ускорение точки тела, вращающегося вокруг неподвижной оси,

.

Его численное значение (модуль) определяется по формуле:



Таким образом, модули скоростей и ускорений точек тела, вращающегося вокруг неподвижной оси, прямопропорциональны кратчайшему расстоянию от них до оси вращения, причем, чем дальше находится точка от оси вращения, тем больше ее скорость иускорение.