!Конспект лекций Теоретичекая и прикладная механика. Лекция 1 Предмет теоретической механики. Кинематика точки
 Скачать 3.52 Mb.
|
|
ГЛОССАРИЙ
Домашнее задание – рассмотреть самостоятельно преобразование простейших движений (передаточные механизмы). Cм. Курс теоретической механики (под ред. академика К.С.Колесникова ), Москва, издательство МГТУ имени Н.Э.Баумана,2000- 82-84с. М.И Бать, Г.Ю.Джанелидзе, А.С.Кельзон Теоретическая механика в примерах и задачах, 1 часть,Москва,1975 – 286-300с. Лекция 3. Плоское движение твердого тела Цель лекции – изложить плоское движение твердого тела с выводом теорем о скоростях и ускорениях точек плоской фигуры на основе анализа движения плоской фигуры в ее плоскости. План лекции Плоское движение твердого тела. Разложение плоского движения на простейшие движения. Независимость вращательного движения плоской фигуры от выбора полюса. Теорема о скоростях точек плоской фигуры. Теорема об ускорениях точек плоской фигуры. КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Плоским движением твердого тела называется такое движение, при котором все его точки движутся в плоскостях, параллельных данной неподвижной плоскости. Плоское движение часто встречается в технике. Большинство современных механизмов имеет звенья, совершающие плоские движения. Такие механизмы называются плоскими. Плоское движение твердого тела иногда называют плоско-параллельным движением. Если тело, находящееся в состоянии плоского движения, пересечь плоскостью, в которой лежит траектория какой-нибудь из его точек, то плоская фигура, получившаяся от пересечения тела во время движения тела, будет передвигаться в этой плоскости. Движения точек тела, лежащих на перпендикуляре, восстановленном к плоскости фигуры, совершенно одинаковы, а потому движение тела может быть охарактеризовано движением фигуры в ее плоскости, и для исследования плоского движения твердого тела достаточно исследовать движение плоской фигуры. Перемещение фигуры из одного положения в другое можно разложить на поступательное движение вместе с произвольной ее точкой, называемой полюсом, и вращение плоской фигуры вокруг оси, проходящей через выбранный полюс. В самом деле, выберем за полюс, например, точку А (рис.1). Тогда при поступательном движении фигуры отрезок АВ, перемещаясь параллельно самому себе, займет положение А1В*1. Повернув отрезок на угол  , совместим его с отрезком А1В1 плоской фигуры в новом положении, обеспечив тем самым рассматриваемое движение плоской фигуры. Аналогичный результат получается, если выбрать за полюс точку В.Важно отметить, что тогда как поступательная составляющая плоского движения тела в общем случае различна для разных точек тела, величина и направление угла поворота плоской фигуры всегда одни и те же, т.е. они не зависят от выбора полюса. 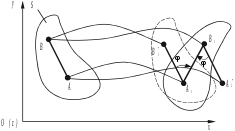 Рис.1 Уравнения  определяющие положение и движение плоской фигуры в неподвижной плоскости Oxy, называютсяуравнениями плоского движения твердого тела. Введем понятия алгебраической угловой скорости  и алгебраического углового ускорения  плоского движения твердого тела: .Представим положение плоской фигуры и ее отрезка АВ в неподвижной системе координат Oxyz(рис.2). Для произвольного момента времени запишем векторное равенство 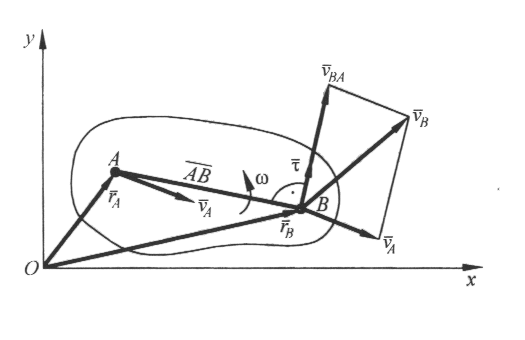  Рис. 2 При движении плоской фигуры векторы  и  изменяются и по модулю, и по направлению, вектор же  изменяется только по направлению, так как его модуль равен постоянному для твердого тела растоянию между точками А и В. Запишем производную по времени от обеих частей векторного равенства:  Обозначив  и назвав скоростью точки В тела при вращении вокруг полюса А, получим  Рассмотрим вектор  . где , направленный в сторону возрастания угла поворота  . Тогда вектор лежит в плоскости движущейся фигуры и  . Модуль вектора  . Обозначив  , запишем:  . Применим формулу Эйлера:  .Окончательно имеем:  . Таким образом, скорость какой-либо точки фигуры при ее плоском движении равнв векторной сумме скорости полюса и скорости этой точки при вражении фигуры вокруг полюса. Перейдем к определению ускорений точек плоской фигуры. Продифференцировав выражение, полученное для скорости, по времени, получим  Здесь   - ускорения точек В и А относительно неподвижной системы координат;  - ускорение точки В при вращательном движении плоской фигуры вокруг подвижной оси, проходящей через полюс А. Таким образом,  , т.е. ускорение какой-либо точки плоской фигурыпри плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении плоской фигуры вокруг полюса.Учитывая, что  найдем:  , где  - угловое ускорение тела при плоском движении. Слагаемые вектора  есть касательная и нормальная составляющие: модули которых  .  , вектор  направлен от В к полюсу А. Таким образом, Обозначив угол между ускорением 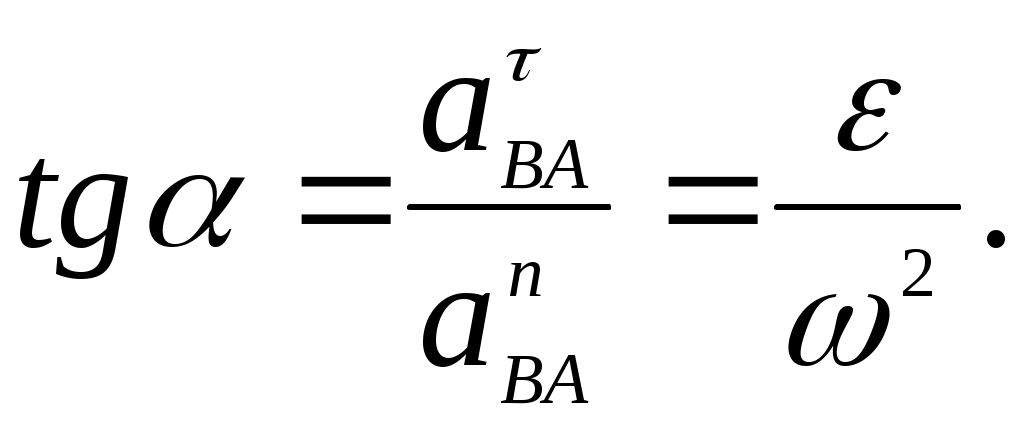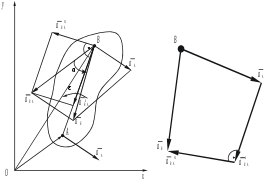и отрезком АВ через  , найдем   Рис.3 ГЛОССАРИЙ
Домашнее задание - самостоятельно изучить: 1) теорему о равенстве проекций скоростей (основную теорему кинематики); 2) мгновенный центр скоростей (МЦС) и рассмотреть различные случаи определения положения МЦС. Cм. Курс теоретической механики (под ред. академика К.С.Колесникова ), Москва, издательство МГТУ имени Н.Э.Баумана,2000- 72-73с; 90-94с. Лекция 4. «Сложное движение точки» Цель лекции – изложить сложное движение точки с доказательством теоремы Кориолиса. План лекции Введение в кинематику сложного движения точки. Теорема сложения скоростей Теорема сложения ускорений (теорема Кориолиса). Свойства ускорения Кориолиса. Правило Н.Е.Жуковского КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Механическое движение выражается в изменении с течением времени взаимных положений тел.Такое изменение можно отметить только относительно других тел. В ряде задач механики оказывается целесообразным рассмотрение движения точки одновременно в нескольких системах координат, одна из которых принимается за неподвижную. Движение точки, исследуемое одновременно по отношению к основной и подвижной системам отсчета, называют сложным. Введем следующие определения. Движение точки по отношению к подвижной системе отсчет называется относительным. Кинематические характеристики этого движения называются соответственно относительной скоростью  и относительным ускорением  .Движение, совершаемое подвижной системой отсчета и всеми неизменно связанными с нею точками пространства по отношению неподвижной системе называется переносным, соответственно и характеристики движения будут называться переносной скоростью  и переносным ускорением  .Зависимость между абсолютной  , относительной и переносной скоростями точки в сложном ее движении устанавливает теорема о сложении скоростей.Теорема. Абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей. Доказательство. Действительно, поскольку для любого момента времени (рис.1)  ,т 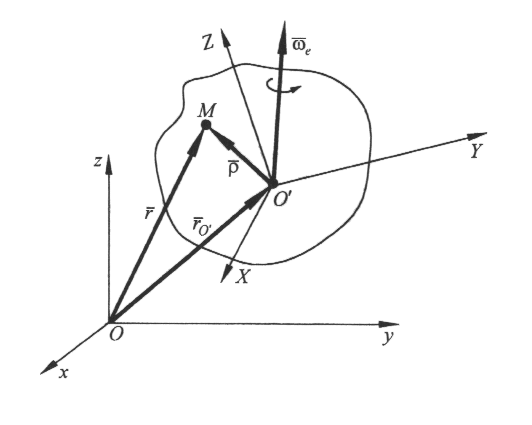 о, продифференцировав по времени это векторное уравнение, получим г Рис.1 де  и  - полные производные, причем  есть абсолютная скорость точки М;  скорость точки О/. Согласно формуле Бура, З Рис.1 Рис.1 десь  представляет собой относительную скорость точки М. Таким образом,  Поскольку  вектор переносной скорости точки М, то, следовательно, Найдем зависимость между абсолютным, относительным и переносным ускорениями точки. С учетом последнего соотношения абсолютное ускорение точки  , здесь  и  - полные производные векторов  и  , записанные для неподвижной системы координат. Воспользовавшись формулой Бура, имеем 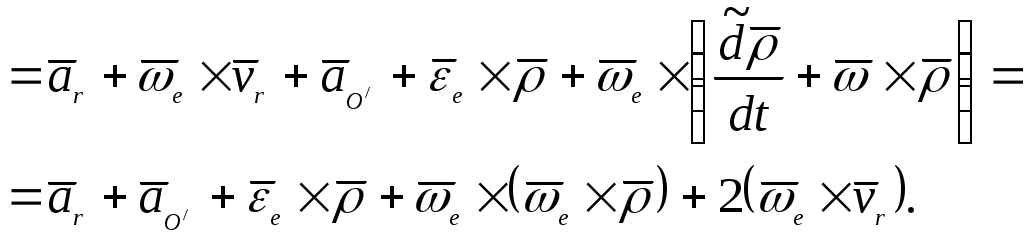  Так как  , получаем:  , или  , где  есть ускорение Кориолиса.Предпоследняя формула выражает теорему о сложении ускорений, или кинематическую теорему Кориолиса: абсолютное ускорение точки является векторной суммой трех ускорений: относительного, переносного и ускорения Кориолиса. Модуль ускорения Кориолиса, если угол между векторами  и обозначить  , будет равен Направление вектора  определяется правилом векторного умножениялибо правилом Жуковского, согласно которого следуетспроектировать вектор относительной скорости на плоскость, перпендикулярную оси переносного вращения и повернуть эту проекцию в этой же плоскости на 900 в сторону переносного вращения (рис.2).Ускорение Кориолиса равно нулю в следующих случаях: 1) 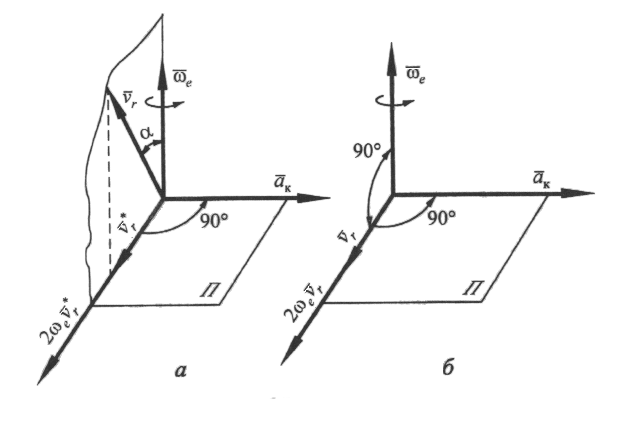 , т.е. переносное движение - поступательное; 2)  т.е. в те моменты времени, когда в относительном движении точка останавливается, например, при изменении направления относительного движения; 3)  т.е.  . Рис.2 ГЛОССАРИЙ
|