!Конспект лекций Теоретичекая и прикладная механика. Лекция 1 Предмет теоретической механики. Кинематика точки
 Скачать 3.52 Mb. Скачать 3.52 Mb.
|
|
Теорема. Произвольную систему сил, действующих на твердое тело, можно привести к какому-либо центру, заменив все действующие силы одной силой, равной главному вектору системы сил, приложенному в этом центре, и одной парой сил с моментом, равным главному моменту системы сил относительно того же цетра. Доказательство. Пусть на твердое тело действует произвольная система сил 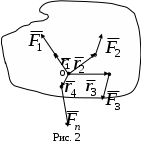 Систему пар сил можно заменить одной парой, момент которой равен главному моменту системы сил относительно центра привеления. Итак, всякая система сил, приложенных к твердому телу, эквивалентна одной силе, называемо главным вектором и одной паре, момент которой называют главным моментом Теорема доказана. Из теоремы о приведении системы сил к силе и паре сил, можно вывести условия равновесия системы сил, действующих на твердое тело. Для равновесия системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен нулю и главный момент системы сил относительно любого центра приведения также был равен нулю, т.е. Эти условия являются векторными условиями равновесия для любой системы сил. Условия равновесия пространственной системы сил в аналитической форме 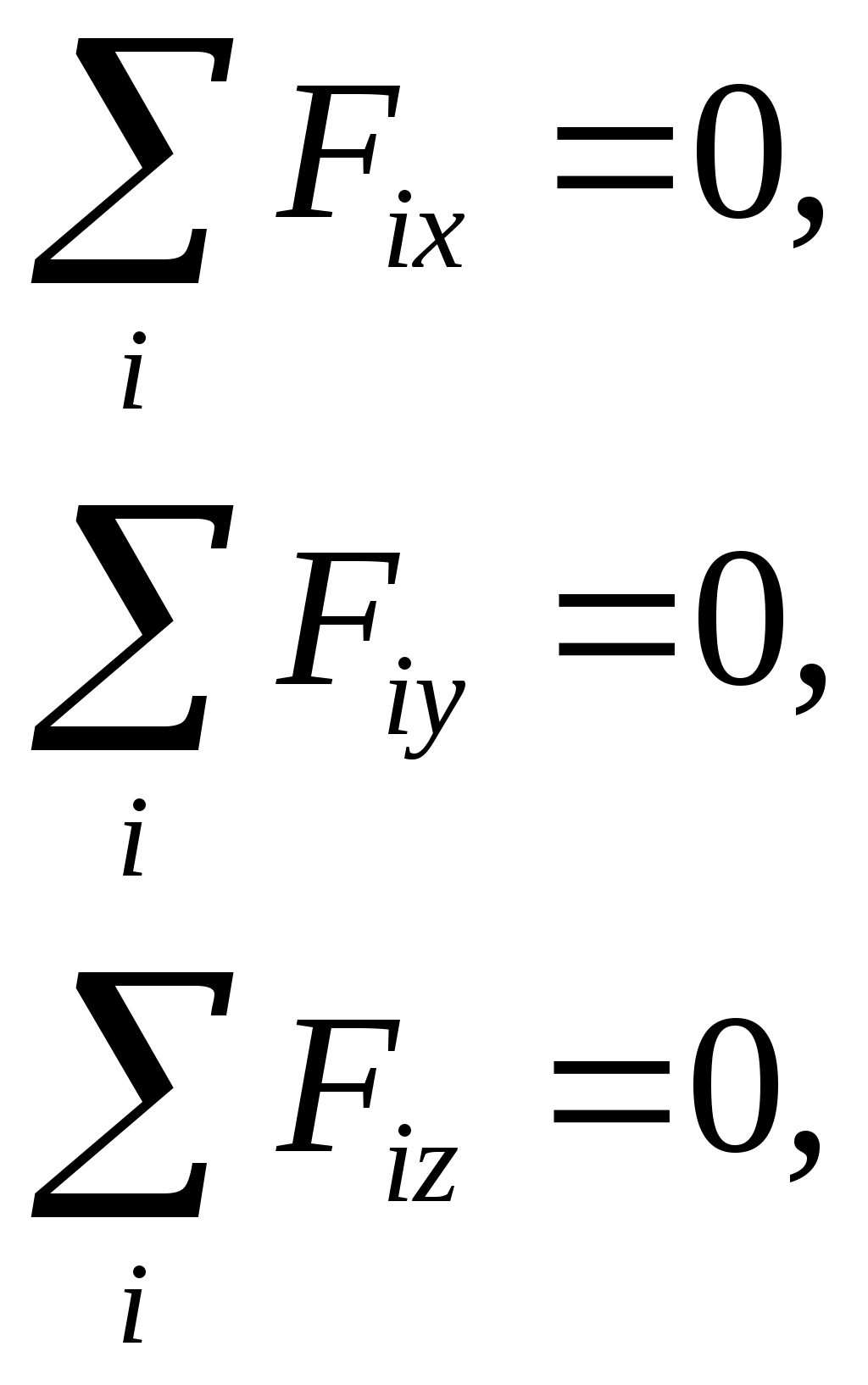 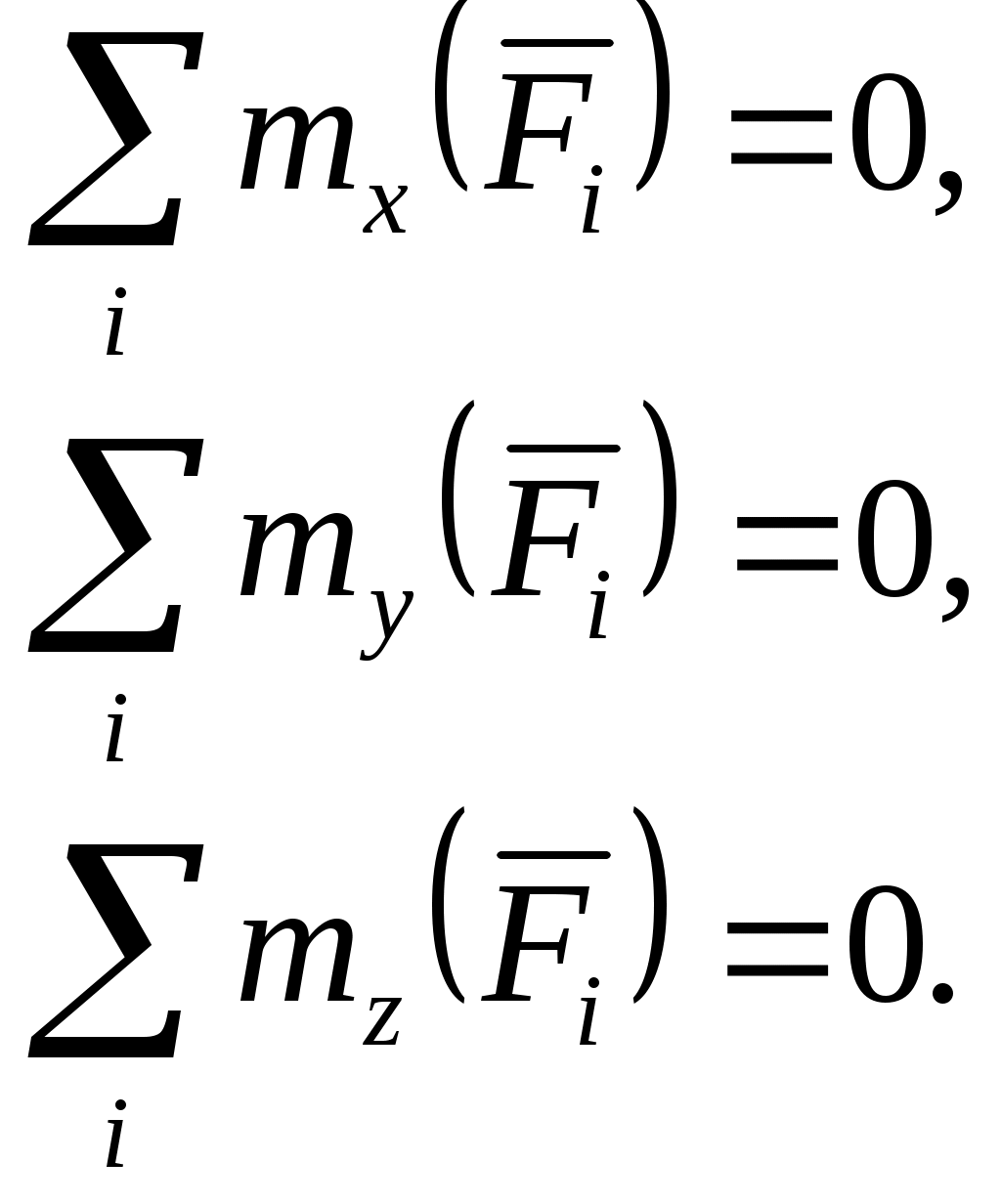 Условия равновесия плоской системы сил: 1) 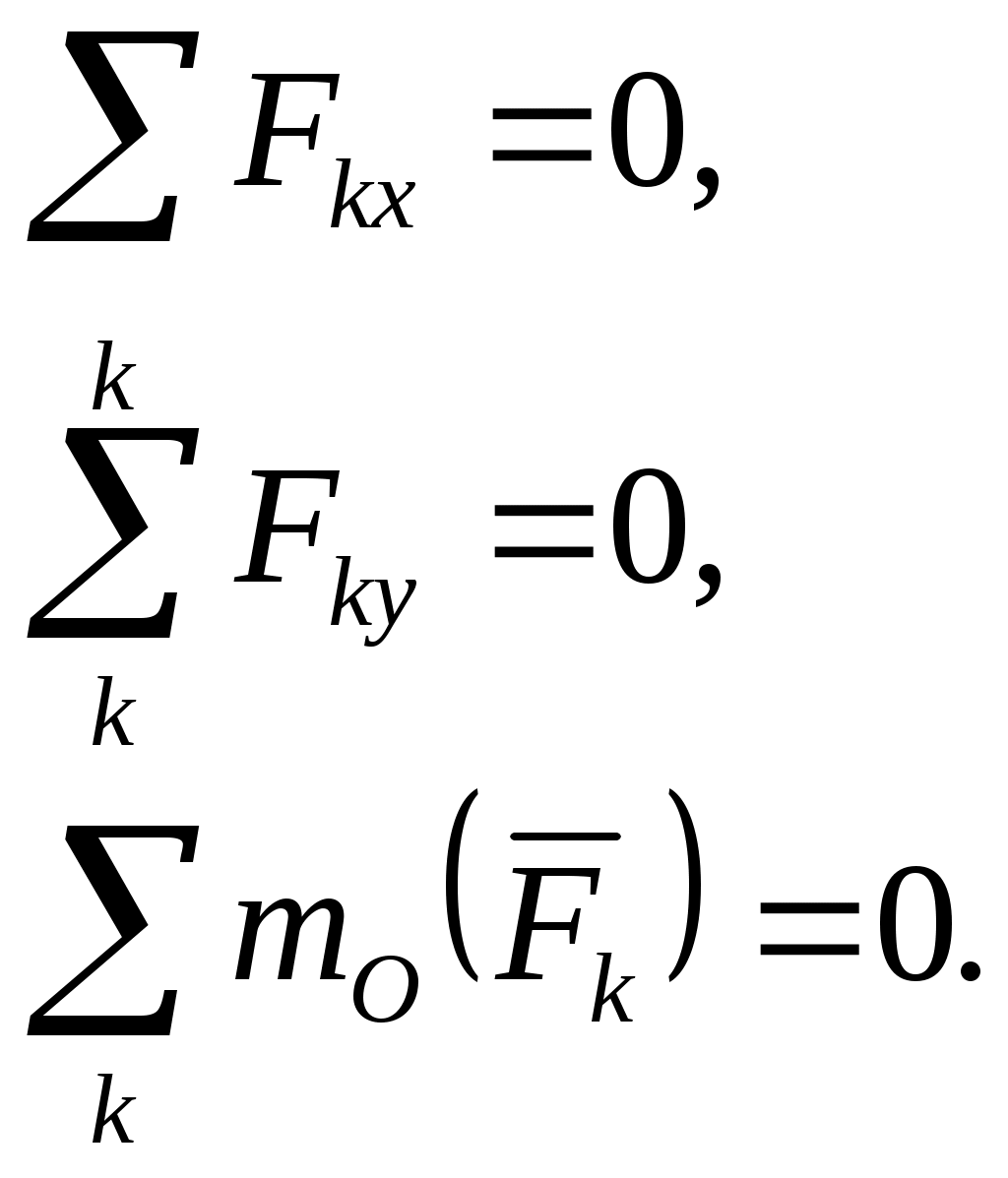 2) 2) 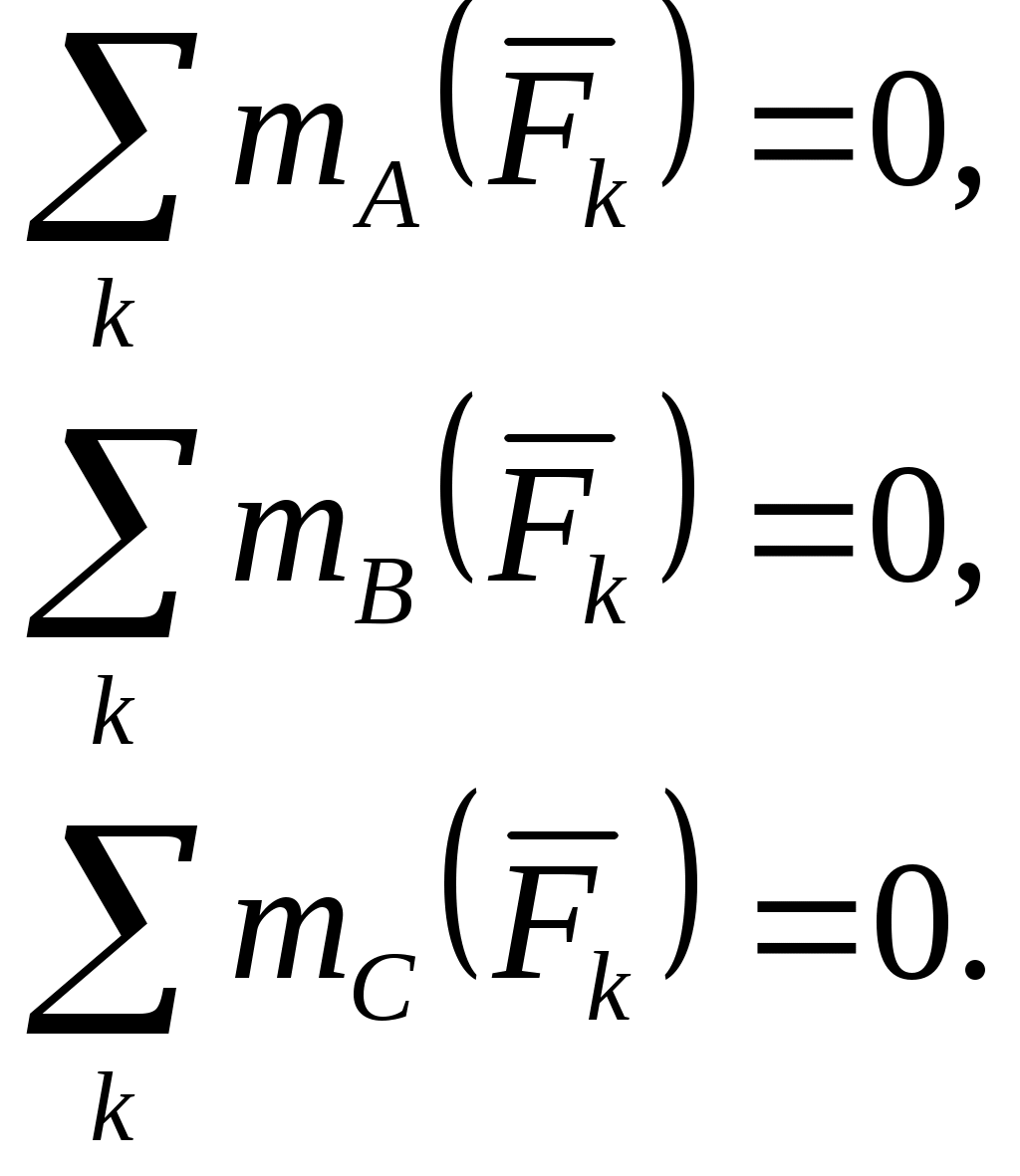 точки А,В, С – не лежат на одной прямой. точки А,В, С – не лежат на одной прямой.3) 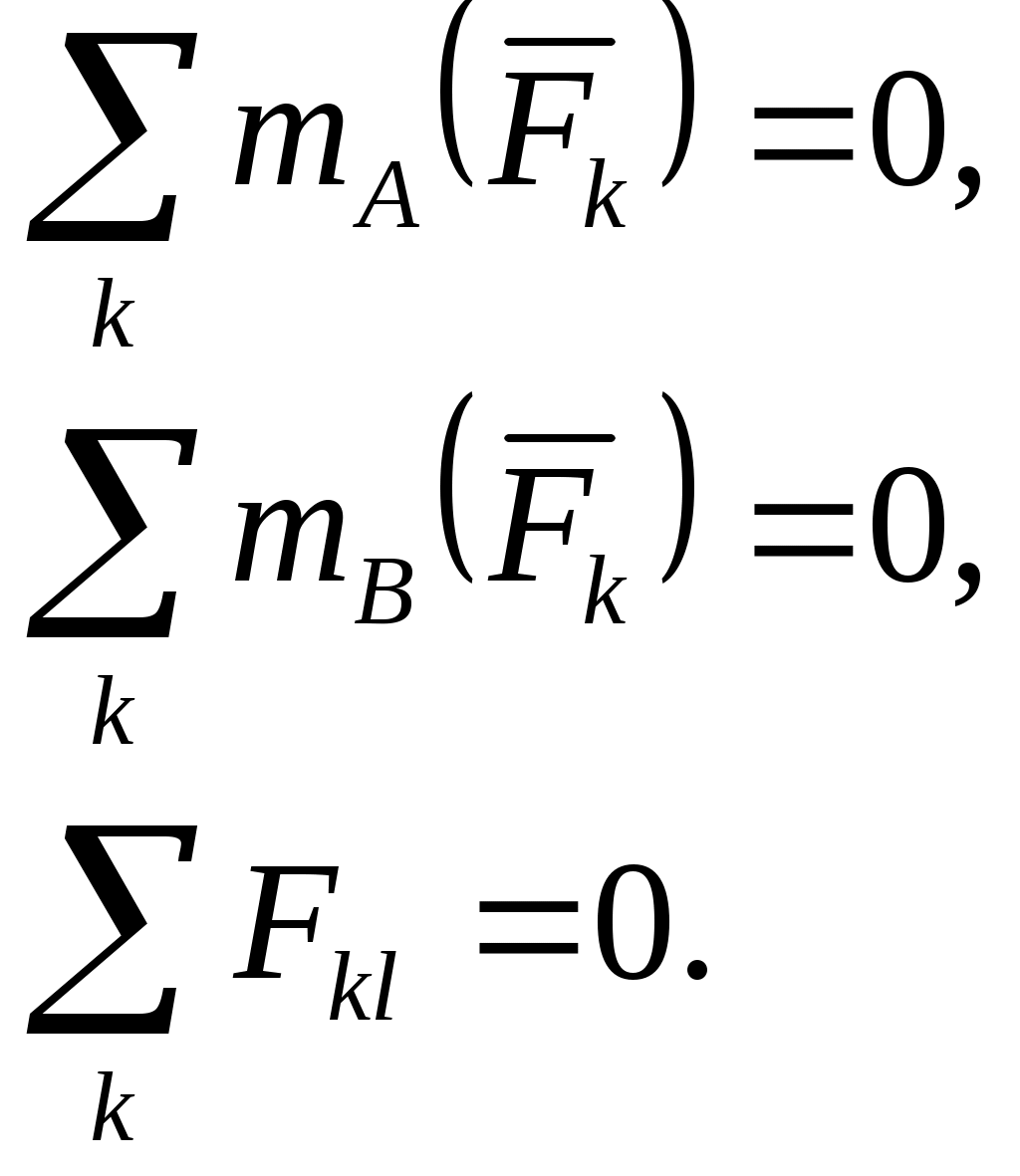 l не должна быть перпендикулярна АВ l не должна быть перпендикулярна АВ ГЛОССАРИЙ
Домашнее задание – самостоятельно получить условия равновесия системы параллельных сил (для плоской системы сил, для пространственной системы сил). Cм. Н.Н.Никитин Курс теоретической механики. Москва, «Высшая школа»,1990 – с.46-48. Лекция 8. Трение. Равновесие тел с учетом сил трения Цель лекции – изложить основные моменты из теории трения, рассмотреть равновесие тел с учетом сил трения. План лекции Сцепление и трение скольжения. Пример. Трение качения. Пример При стремлении сдвинуть одно тело по поверхности другого, в плоскости их соприкосновения возникает сила сцепления (сила трения покоя) При скольжении тела по поверхности другого также возникает сила, препятствующая этому движению, — сила трения скольжения Если же тело катить (или стремиться катить) по поверхности другого тела, то из-за деформации поверхностей тел возникает пара сил, препятствующая качению. К твердому телу, покоящемуся на шероховатой горизонталь ной плоскости, приложим силу причем величина силы пусть будет такова, что тело остается в покое. Это состояние тела обусловлено появлением силы сцепления у прижатых друг к другу тел. Ввиду равновесия Тело останется в покое при изменении модуля силы Sот нуля до некоторого значения Sмах, при котором возникает движение (скольжение). Соответственно и сила сцепления (сила трения покоя) принимает значение от нуля до максимального значения Fпр,, называемого предельной силой трения, т. е. Приложенная к телу сила трения направлена в сторону, противоположную той, куда действующие на тело силы стремятся его сдвинуть. Предельная сила трениячисленно равна произведению статического коэффициента трения (коэффициента сцепления) на нормальное давление тела на поверхность или нормальную реакцию: Статический коэффициент трения Значение предельной силы трения не зависит от размеров соприкасающихся при трении поверхностей. Величине При малейшем превышении модуля силы При скольжении тела по шероховатой поверхности к нему приложена сила трения скольжения. Направление этой силы противоположно направлению скорости тела, а модуль силы трения скольжения определяется произведением коэффициента трения на нормальное давление: Коэффициент трения скольжения (динамический коэффициент трения) Реакция Rшероховатой поверхности имеет две составляющие: нормальную реакцию N и перпендикулярную ей силу трения (при покое тела — это сила сцепления, при движении — это сила трения скольжения). Следовательно, полная реакция Rбудет отклонена от нормали к поверхности на некоторый угол Если под действием приложенных сил тело находится в покое, то величина силы трения согласно неравенству может принимать значения от нуля до Так как Таким образом, при равновесии тела полная реакция Rпроходит внутри угла трения Рассмотрим задачу, которая позволит указать некоторую физическую интерпретацию угла трения. 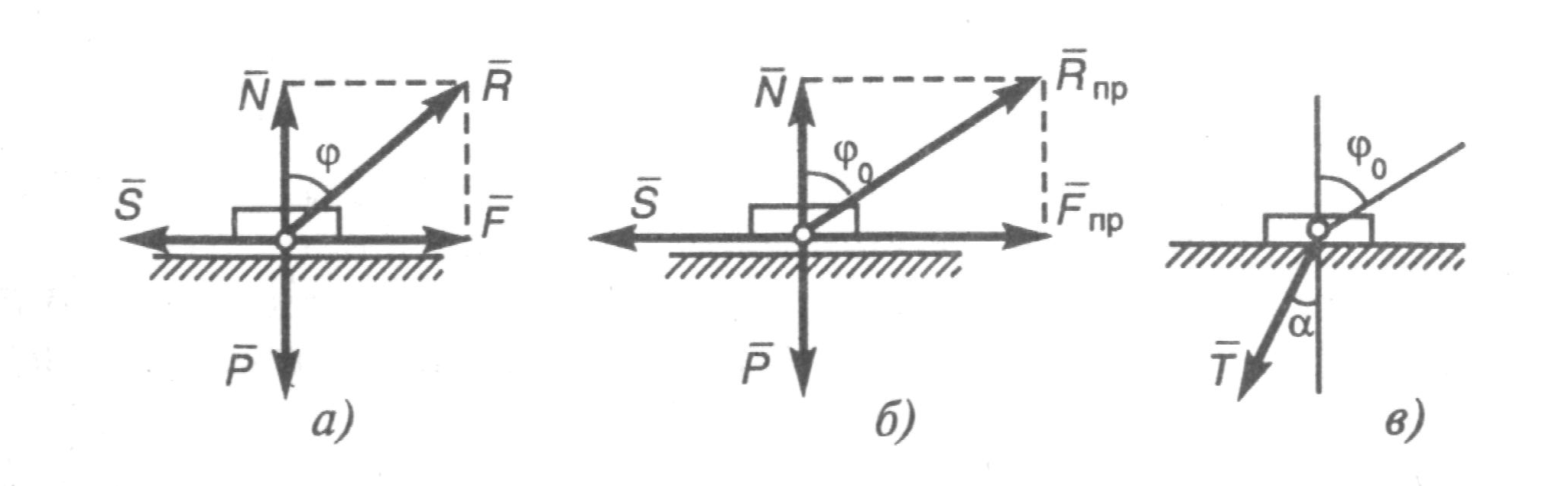 Рис.1 Рис.1Пример 1. Определить, при каких значениях угла наклона Решение. Сначала определим значение угла Решив эти уравнения, получим N=Pcos F=Ntg Отметим, что эти результаты справедливы только при равновесии, т. е. при значениях угла При отсюда Груз на наклонной плоскости будет находиться в равновесии при 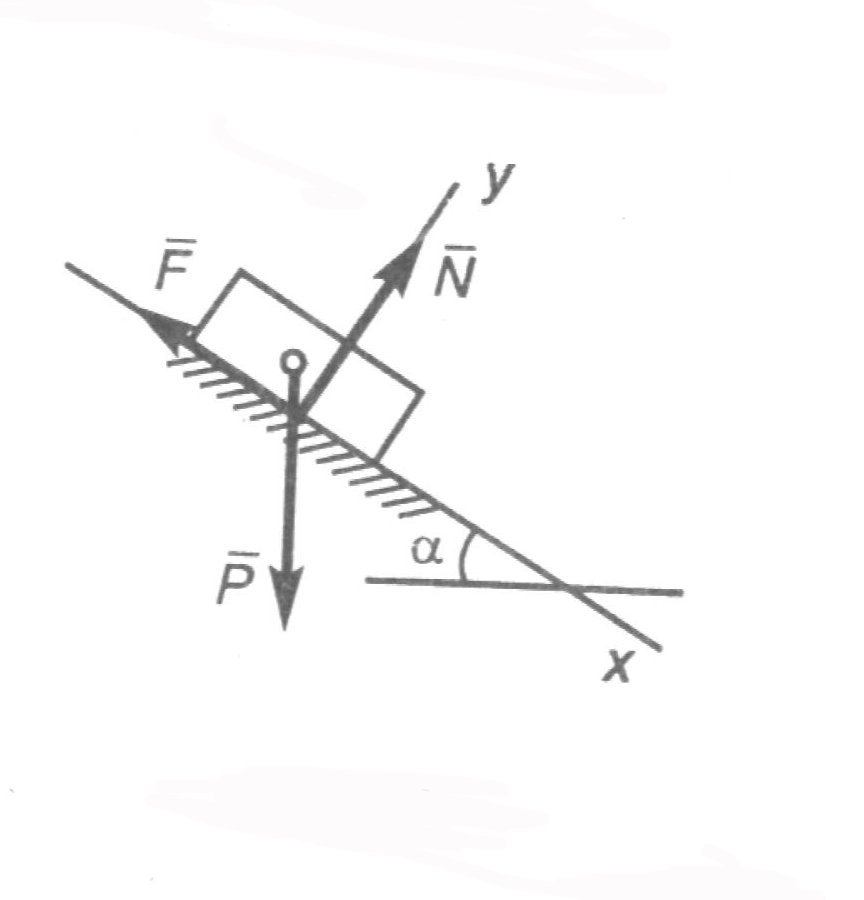 Так как Так как Обращаем внимание, что при всех расчетах предельных состояний равновесия тела величину Трением каченияназывается сопротивление, возникающее при качении одного тела по поверхности другого. Пусть круглый цилиндрический каток радиусом Rи весом Р находится на шероховатой горизонтальной поверхности. Приложим к оси катка силу Q(рис. 3,а), меньшую Дело в том, что фактически вследствие деформаций тел их касание происходит по некоторой площадке BD(рис. 3,б), интенсивность давления по которой у края В больше, чем у края D. В результате реакция N (равнодействующая этих давлений) оказывается смещенной в сторону действия силы Q. С увеличением Qэто смещение возрастает до некоторой предльной величины 8. Таким образом, в предельном положении равновесия катка пара сил Fуравновешивается парой N, Р: отсюда 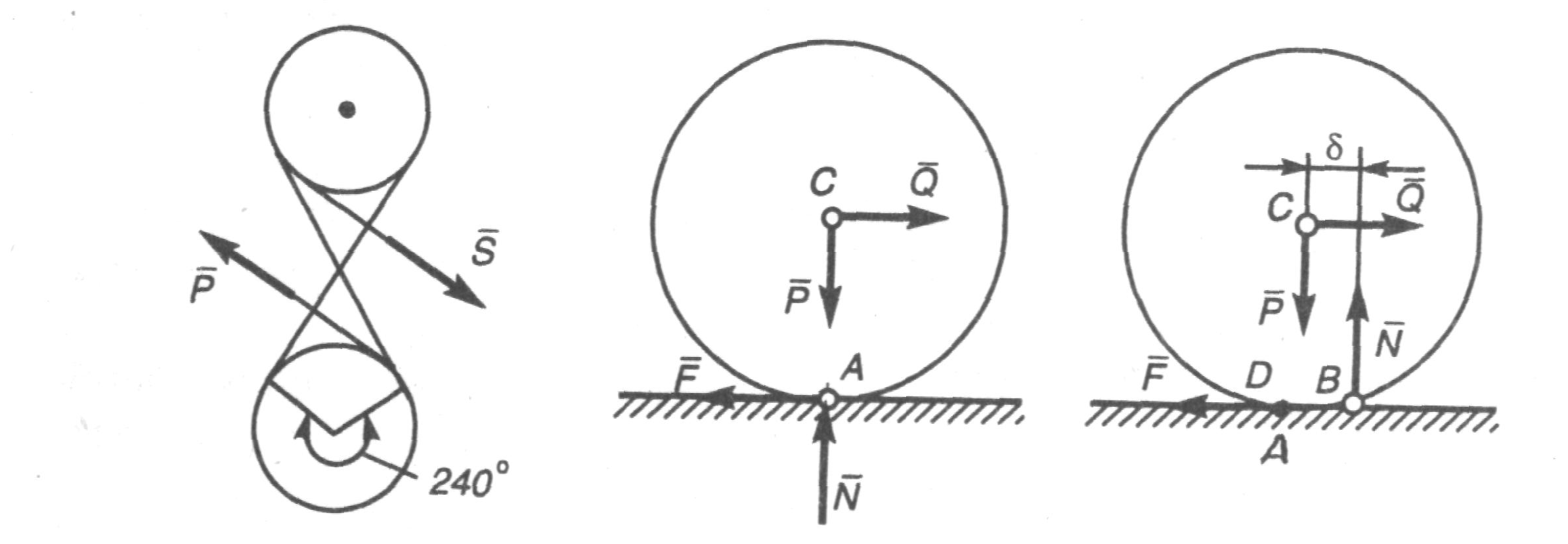 Рис.3 Пока При выполнении расчетов следует также учитывать, что сила При равновесии катка Q=F\ отсутствие скольжения и качения будет при одновременном выполнении двух условий: Для большинства материалов отношение каток катится без скольжения. При Q> Таким образом, для большинства материалов преодолеть сопротивление качению значительно легче, чем преодолеть сопротивление скольжению. Этим объясняется то, что в технике стремятся скольжение заменить качением (колеса, катки, шариковые и роликовые подшипники и т. п.). Пример 2. Цилиндрический каток радиусом Rи весом Р (рис. 4, а) удерживается в равновесии на наклонной плоскости нитью, перекинутой через блок. К концу нити подвешен груз весом Q. Коэффициент трения качения катка равен 3, угол наклона плоскости к горизонту равен а. Определить наименьшую и наибольшую величины веса Q, при которых каток будетв равновесии. Решение. Рассмотрим равновесие катка в двух предельных случаях..В первом случае, когда величина Q(натяжение нити численно равное весу груза)имеет наибольшее значение Составим уравнение моментов относительно точки А: 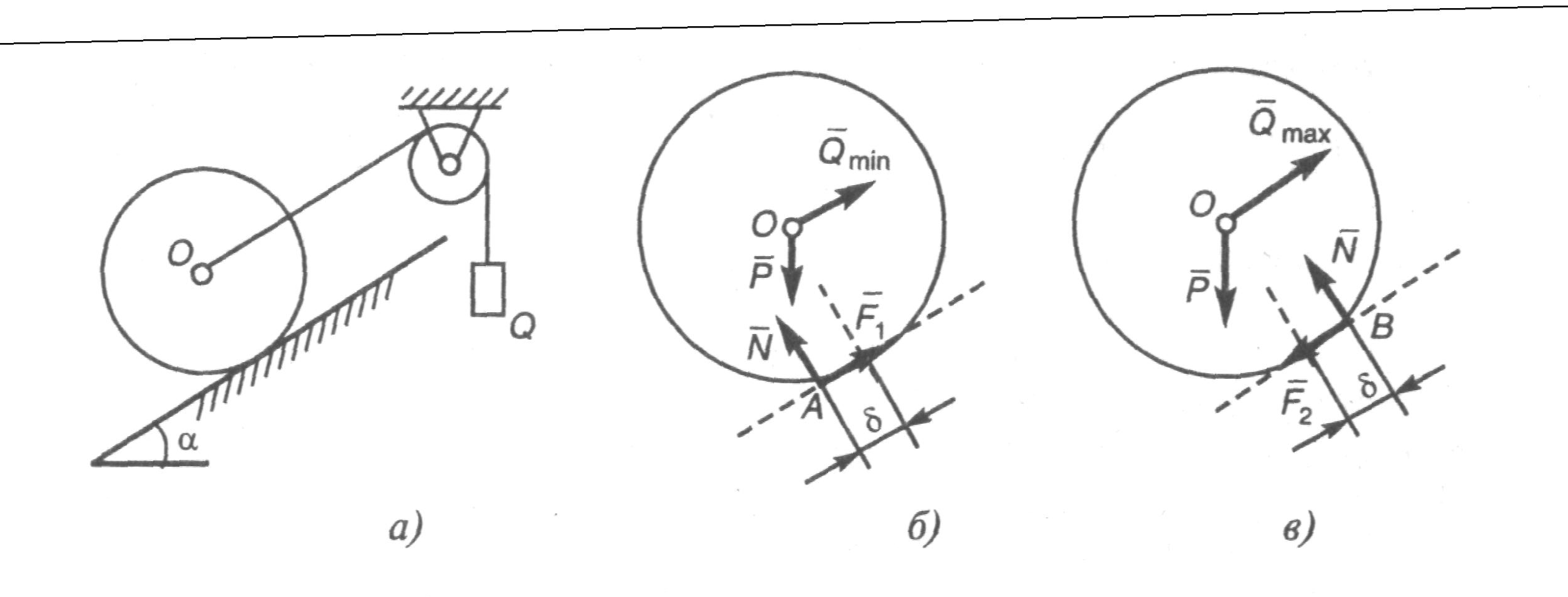 Рис. 4 Отсюда получим Теперь рассмотрим второй случай предельного равновесия катка, когда сила Qдостигает наибольшего значения, Отсюда получим Таким образом, каток будет находиться в равновесии на наклонной плоскости, если величина силы Qлежит в пределах Легко установить, что в обоих случаях N=Pcos Домашнее задание – самостоятельно ответить на следующие вопросы: 1) Груз весом См. Курс теоретической механики (под ред. академика К.С.Колесникова ), Москва, издательство МГТУ имени Н.Э.Баумана,2000- с.236-239. Лекция 9. Динамика материальной точки Цель лекции – изложить основные законы динамики, рассмотреть две задачи динамики точки План лекции Предмет динамики. Основные законы динамики Дифференциальные уравнения движения материальной точки. Две задачи динамики КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Динамика является основным и наиболее общим разделом теоретической механики. В динамике изучают зависимость между движением материальных объектов и действующими на них силами. Соотношения между основными понятиями динамики определяются аксиомами или основными законами движения, данными Ньютоном. 1 закон. Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. 2 закон (основной). Ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силе и совпадает с ней по направлению. Математически этот закон можно записать в виде где 3 закон (действия и противодействия). Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны. Если на материальную точку лействует система сил где Так как ускорение точки связано с ее радиус-вектором В проекциях на декартовы оси (базис 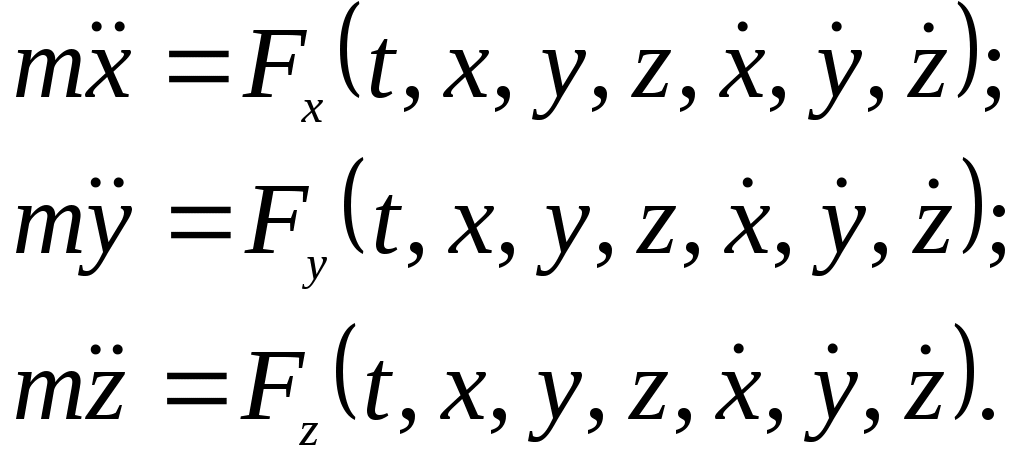 (3) (3)Здесь Первым интегралом системы дифференциальных уравнений (3) является функция называется производной по времени функции Для того чтобы полностью найти закон движения материальной точки, достаточно найти шесть функционально независимых первых интегралов. Действительно, пусть 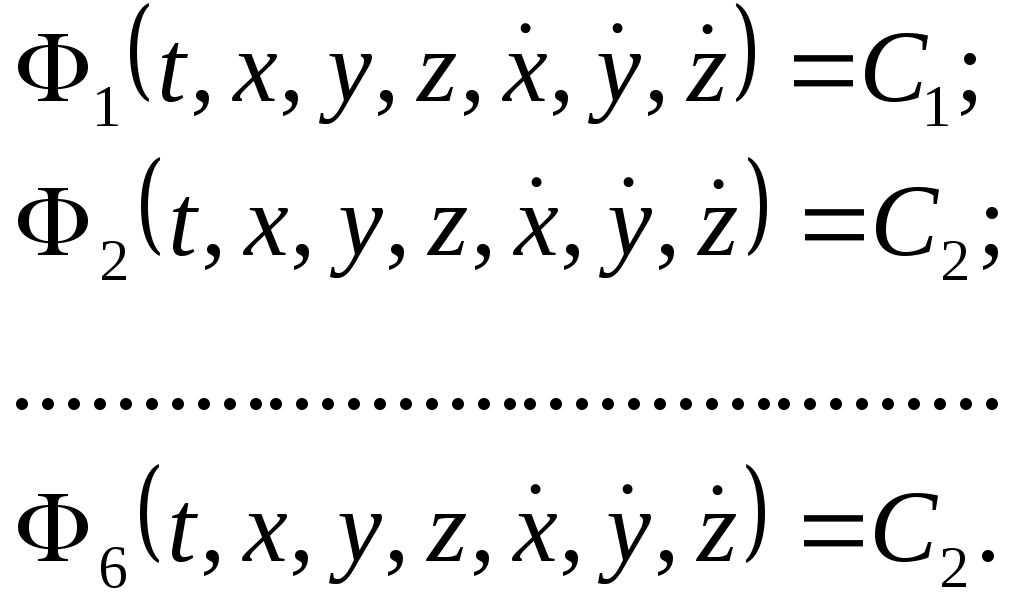 - шесть независимых первых интегралов системы (3). Тогда Знание первого интеграла позволяет понизить порядок системы. В частных случаях дифференциальных уравнений движения точки может быть меньше. Так, при движении точки в плоскости Оху уравнений движения будет два: В случае движения точки по прямой будем иметь одно дифференциальное уравнение, например: В проекциях на естественные оси ( ГЛОССАРИЙ
Домашнее задание – рассмотреть и решить следующую задачу самостоятельно: груз массой См. Н.Н.Никитин Курс теоретической механики Москва, «Высшая школа»,1990 - с.235-255 Лекция 10. Введение в динамику системы. Геометрия масс Цель лекции – изложить основные понятия динамики механической системы, дать основные понятия геометрии масс. План лекции Механическая система. Внешние и внутренние силы Масса системы. Центр масс Моменты инерции. Теорема Штейнера |
