!Конспект лекций Теоретичекая и прикладная механика. Лекция 1 Предмет теоретической механики. Кинематика точки
 Скачать 3.52 Mb.
|
|
Домашнее задание – показать применение правила Жуковского на определение ускорений Кориолиса на примере движущихся точек по поверхности Земли по меридианам и параллелям в разных направлениях. Cм. Курс теоретической механики (под ред. академика К.С.Колесникова ), Москва, издательство МГТУ имени Н.Э.Баумана,2000-736с. Лекция 5 Введение в статику. Основные понятия и аксиомы статики Цель лекции – ознакомить с основными понятиями статики, изложить аксиомы, рассмотреть основные виды связей План лекции Введение в статику. Основные понятия и определения Аксиомы статики Основные виды связей и их реакции КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Статика – это раздел теоретической механики, в которой изучаются методы эквивалентных преобразований систем сил и устанавливаются условия равновесия сил, приложенных к твердому телу. При изучении равновесия используют принцип неизменности геометрических форм и размеров твердых тел, поскольку их изменение под действием сил обычно мало по сравнению с первоначальными размерами. Поэтому в статике материальные тела считают абсолютно твердыми. Понятие «сила» в механике является одним из важнейших. Силой называется векторная величина, являющаяся мерой механического воздействия одного материального тела на другое. Векторная сила характеризуется числовым значением, или модулем, и направлением действия. Единицей измерения силы является 1 ньютон (1Н). Прямая, вдоль которой направлена сила, называется линией действия силы. Приведем основные определения статики. Системой сил называется совокупность сил, действующих на твердое тело. Если систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом механического состояния тела, то такие две системы сил называются эквивалентными. Система сил, под действием которой свободное тело может находиться в покое, называется уравновешенной, или эквивалентной нулю. Если система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Силы, действующие на данное тело или систему тел, можно разделить на внешние – силы, силы, действующие на данную систему со стороны других тел, не входящих в рассматриваемую систему, и внутренние – силы, с которыми действуют друг на друга тела, входящие в рассматриваемую систему. Механической системой называется любая совокупность взаимодействующих материальных точек. Статика базируется на основных законах, принимаемых без математических доказательств и называемых аксиомами статики. Аксиома 1. Если на свободное твердое тело действуют две силы, то тело может находиться в равновесии только тогда, когда эти силы равны по модулю, действуют по одной прямой в противоположные стороны.. Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменяется, если к ней добавить или от нее отнять уравновешенную систему сил. Аксиома 3. При всяком действии одного материального тела на другое со стороны другого тела имеется противодействие, такое же по величине, но противоположное по направлению. Аксиома 4. Две силы, приложенные к твердому телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах как на сторонах. Аксиома 5. Механическое состояние не изменится, если освободить ее от связей, приложив к точкам системы силы, равные реакциям связей. Эту аксиому называют аксиомой о связях. Материальные тела, ограничивающие перемещение данного тела в пространстве, называют связями. Сила, с которой связь действует на тело, препятствуя его перемещениям, называется силой реакцией связи, или просто реакцией связи. Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу. 1. Гладкая поверхность (плоскость). Реакция 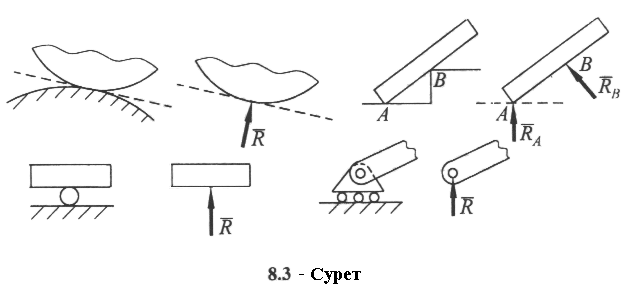 в случае гладкой поверхности направлена по общей нормали к поверхностям связи и тела в точке их контакта и приложена к телу. На рисунке показаны некоторые примеры направления реакций.  2. Гибкие связи. Этим термином обозначают цепи, тросы, канаты, которые могут воспринимать только силы растяжения. 3.Цилиндрический шарнир (подшипник). Цилиндрический шарнир представляет собой цилиндрическую втулку, в которой находится ось вращения. Он не воспринимает осевой силы, его реакция находится в плоскостиAxy, перпендикулярной оси шарнира. Реакция 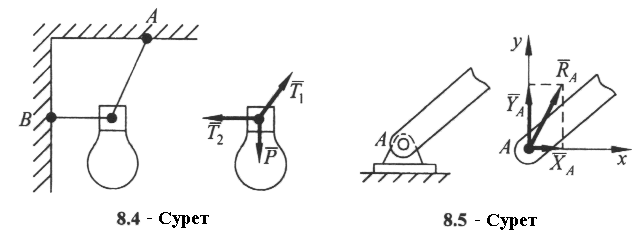 может быть направлена по любому радиусу шарнира в плоскости Axy. 4. Сферический шарнир. Он позволяет телу поворачиваться, но не разрешает линейные перемещения. Реакция шарнира 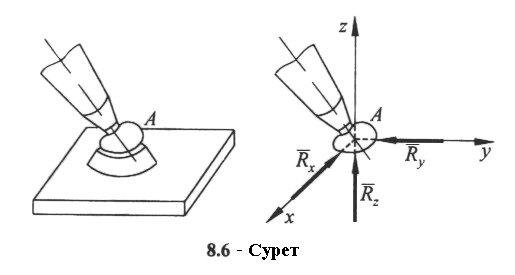приложена к его центру и может быть направлена по любому радиусу шарнира. 5. Подпятник. Он отличается от цилиндрического шарнира тем, что кроме радиальных сил может воспринимать и осевую силу. Реакция подпятника, как и реакция сферического шарнира, может иметь любое направление.  6. Невесомый стержень с шарнирами на концах. Реакция прямолинейного невесомого стержня с шарнирами на концах направлена вдоль оси стержня. В отличие от нити такой стержень может передавать как силы растяжения, так и силы сжатия. Если связью является криволинейный стержень, то его реакция будет направлена по прямой АВ, соединяющий шарниры А и В. При решении задач статики реакции связей обычно являются неизвестными и подлежат определению, а зная силы реакций связей, можно определить внутренние силы в телах, необходимые для расчета на прочность. ГЛОССАРИЙ
Домашнее задание – доказать самостоятельно простейшие теоремы статики. Cм. Курс теоретической механики (под ред. академика К.С.Колесникова ), Москва, издательство МГТУ имени Н.Э.Баумана,2000-174-175с.,188с. Лекция 6. Теория моментов. Элементарная теория пар сил Цель лекции – изложить основные понятия теории моментов сил, пар сил. План лекции Момент силы относительно точки и относительно оси Элементарная теория пар сил КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Если дана сила  , то ее проекции на оси декартовой системы координат будут определяться следующими формулами: Здесь  - единичные вектора. Для направляющих косинусов справедливо следующее соотношение . Из этих трех углов только два независимые. Проецируя силу на ось, необходимо использовать эти углы. Данную силу 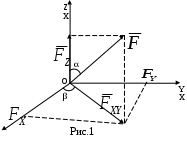разложим на составляющие:  Здесь  .XX Замечание. Проекция силы на плоскость – векторная величина, а проекция силы на ось – скалярная величина. 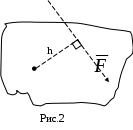 Моментом силы относительно точки называют меру механического воздействия, учитывающую положение силы по отношению к точке и выражающуюся произведением модуля силы на плечо, взятым со знаком плюс или минус. Точку, относительно которой определен момент силы, называют центром момента. Опущенный из центра момента перпендикуляр на линию действия силы является плечом силы. Знак момента силы определяется по следующему правилу: момент считается положительным, когда сила стремится повернуть тело вокруг центра против хода часовой стрелки, когда по ходу часовой стрелки – отрицательным. Отметим следующие свойства момента силы относительно центра: 1) момент силы относительно точки не изменяется при переносе силы вдоль ее линии действия, так как при этом не меняется плечо силы; 2) момент силы относительно точки равен нулю, когда линия действия силы проходит через эту точку (плечо силы равно нулю). Чтобы определить момент силы относительно оси необходимо: провести через произвольную точку О оси плоскость П, перпендикулярную оси; найти проекцию  силы  на плоскость П;определить плечо h силы относительно точки О;вычислить произведение  ;определить знак момента: принимаем его со знаком плюс, если с положительного конца оси поворот, который стремится совершить сила 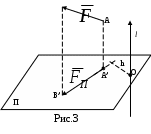, виден против хода часовой стрелки, и со знаком минус – когда по ходу часовой стрелки  Момент силы относительно оси равен нулю: 1) если сила параллельна заданной оси; 2) если линия действия силы пересекает ось. Парой сил называется система двух равных по модулю параллельных сил, направленных в противоположные стороны. Сумма сил пары равна нулю, но пара сил не уравновешена. Кратчайшее расстояние между линиями действия сил пары называется плечом пары сил. Плоскость, в которой действуют силы пары, называется плоскостью действия пары сил. Совокупность нескольких пар сил, действующих на тело, называется системой пар сил. Пара сил не приводится к равнодействующей. Действие пары на твердое тело сводится к вращательному эффекту, мерой которого является векторная величина, называемая моментом пары сил. Модуль этого вектора равен произведению модуля силы пары на ее плечо, т.е.  Перечислим основные свойства пары сил: пару сил можно переносить куда угодно в плоскости действия пары; пару можно переносить из данной плоскости в любую плоскость, параллельную данной; у данной пары можно произвольно менять модули сил и длину плеча, сохраняя неизменным ее момент. Пары сил эквивалентны, если равны векторы-моменты этих пар. Если на тело действует несколько пар с моментами  , то их совокупное воздействие на тело эквивалентно одной паре с моментом Это равенство выражает теорему о сложении пар. ГЛОССАРИЙ
Домашнее задание – доказать самостоятельно свойство пары сил о переносе ее в параллельную плоскость Cм. Н.Н.Никитин Курс теоретической механики. Москва, «Высшая школа»,1990 – с.33 Лекция 7. Приведение произвольной системы сил к заданному центру. Условия равновесия системы сил Цель лекции – изложить метод приведения системы сил к простейшей системе (метод Пуансо) и рассмотреть условия равновесия системы сил. План лекции Теорема о параллельном переносе силы Приведение системы сил к заданному центру Условия равновесия системы сил КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Теорема. Силу, приложенную к твердому телу, можно, не изменяя ее действия, перенести параллельно самой себе в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, в которую она переносится. 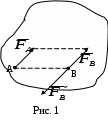 Доказательство. Пусть в точке А тела действует сила (рис.1). Приложив в точке В , куда переносится сила из точки А , эквивалентную нулю систему сил  ( ) получаем силу  и пару сил  , векторный момент которой  ,что и требовалось доказатьТочку, к которой приводят систему сил, называют центром приведения данной системы сил. |