!Конспект лекций Теоретичекая и прикладная механика. Лекция 1 Предмет теоретической механики. Кинематика точки
 Скачать 3.52 Mb.
|
ГЛОССАРИЙ
Домашнее задание - доказать самостоятельно теорему Штейнера. Применить ее к простейшим однородным телам. См. Курс теоретической механики ( под ред. Колесникова К.С.). Москва, издательств о МВТУ им. Н.Э.Баумана,2000-736с. Лекция 11. Дифференциальные уравнения движения механической системы. Теорема о движении центра масс системы Цель лекции – рассмотреть дифференциальные уравнения движения механической системы и теорему о движении центра масс системы. План лекции Дифференциальные уравнения движения механической системы Теорема о движении центра масс механической системы КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Рассмотрим движение механической системы, состоящей из N точек. На точку Mk массой mk системы действует равнодействующая внутренних сил  и равнодействующая внешних сил  (Рис.1). Дифференциальные уравнения движения системы материальных точек в векторной форме имеют вид: 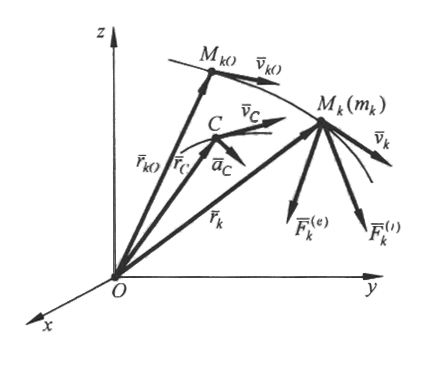 (1)  Рис.1 или   , где  скорость k– ой точки.В проекциях на оси декартовой системы координат Oxyz получаем 3Nдифференциальных уравнений движения механической системы:    . (2)Начальные условия имеют следующий вид: при      (3)Проинтегрировать систему уравнений (2) аналитически т даже численно трудно. Процесс интегрирования еше более усложняет то обстоятельство, что силы реакций связей, наложенных на систему, часто необходимо определять в процессе решения задачи о движении механической системы. Для решения некоторых задач необходимо систему уравнений (1) преобразовать так, чтобы в них содержались зависимости некоторых обобщенных мер движения (количества движения, кинетического момента, кинетической энергии) от характеристик приложенных сил (главного вектора и главного момента относительно центра). Получают эти уравнения из закономерностей, описываемых общими теоремами динамики для механической системы: о движении центра масс, об изменении количества движения,об изменении кинетического момента, об изменении кинетической энергии. Запишем уравнения движения механической системы в виде  (4) где  - ускорение  - ой точки;  - равнодействующие внешних и внутренних сил, действующих на - ую точку. Просуммируем уравнения (4) по всем точкам механической системы: . (5)Здесь  - главный вектор внутренних сил. Продифференцировав дважды по времени выражение (1) для определения радиус-вектора центра масс системы,:  (6) (7) где  - абсолютная скорость центра масс.С учетом (7) уравнение (5) примет вид  , (8) где  - главный вектор внешних сил, действующих на механическую систему.Теорема о движении центра масс механической системы формулируется так: центр масс механической системы движется как материальная точка, как бы обладающая массой системы, под действием всех внешних сил, действующих на точки системы. В проекциях на оси прямоугольной декартовой системы координат уравнения (8) имеют вид    (9) где  - проекции ускорения  центра масс механической системы.Из теоремы о движении центра масс вытекают два следствия: 1. Если главный вектор внешних сил, действующих на систему,равен нулю, т.е. .  , то из (8) следует, что:  , откуда после интегрирования получаем (10)Проинтегрировав еще раз, находим:  (11)Постоянные  определяем из начальных условий:  .Для текущего момента времени при  окончательно имеем   .Таким образом, если главный вектор внешних сил, действующих на механическую систему, равен нулю, то центр масс механической системы движется прямолинейно и равномерно. Если  , т.е. центр масс в начальный момент времени находится в покое, то  (12)2. Пусть теперь проекция главного вектора внешних сил, действующих на систему, на одну из осей (например, ось Ох ) равна нулю  тогда из первого уравнения (9) следует:  , а значит  .Постоянные определяем из начальных условий:  .Для любого момента времени при  окончательно имеем:  ,  .Если  , т.е. проекция скорости центра масс на ось Ох в начальный момент времени равна нулю, то  (13) в любой момент времени. |