!Конспект лекций Теоретичекая и прикладная механика. Лекция 1 Предмет теоретической механики. Кинематика точки
 Скачать 3.52 Mb.
|
|
Домашнее задание – 1) Влияют ли внутренние силы системы на изменение ее кинетической энергии? 2) В каких механических системах сумма работ внутренних сил равна нулю? См. Н.Н.Никитин Курс теоретической механики, Москва «Высшая школа»,1990-607с. Лекция 16. Принцип Даламбера Цель лекции – изложить принцип Даламбера для материальной точки и механической системы План лекции Принцип Даламбера для материальной точки Принцип Даламбера для механической системы Принцип Даламбера сформулирован в 1743 году и первоначально, в отдичие от законов Ньютона, был предназначен для изучения движения несвободных механических систем. В настоящее время этот принцип и вытекающий из него метод кинетостатики рассматривают как удобный прием для определения реакций связей и сил взаимодействия, а также для составления дифференциальных уравнений движения механических систем. В соответствии с аксиомами динамики основное уравнение движения материальной точки имеет вид:  , (1) где  - равнодействующая активных сил;  - равнодействующая реакций связей;  - абсолютное ускорение точки.Уравнение (1) можно также записать в виде  . Слагаемое  обозначают  и называют Даламберовой силой инерции (или просто силой инерции). Основное уравнение динамики материальной точки при использовании силы инерции принимает следующий вид: . (2)Так как указанные выше силы образуют систему сходящихся сил, то уравнение (2) можно рассматривать как условие равновесия системы сил  . В этом и состоит принцип Даламбера для материальной точки: при движении материальной точки в любой момент времени приложенные к ней активные силы и реакции связей вместе с силой инерции образуют систему сил, эквивалентную нулю, т.е. (3)В проекциях на оси декартовой системы координат имеем    , где 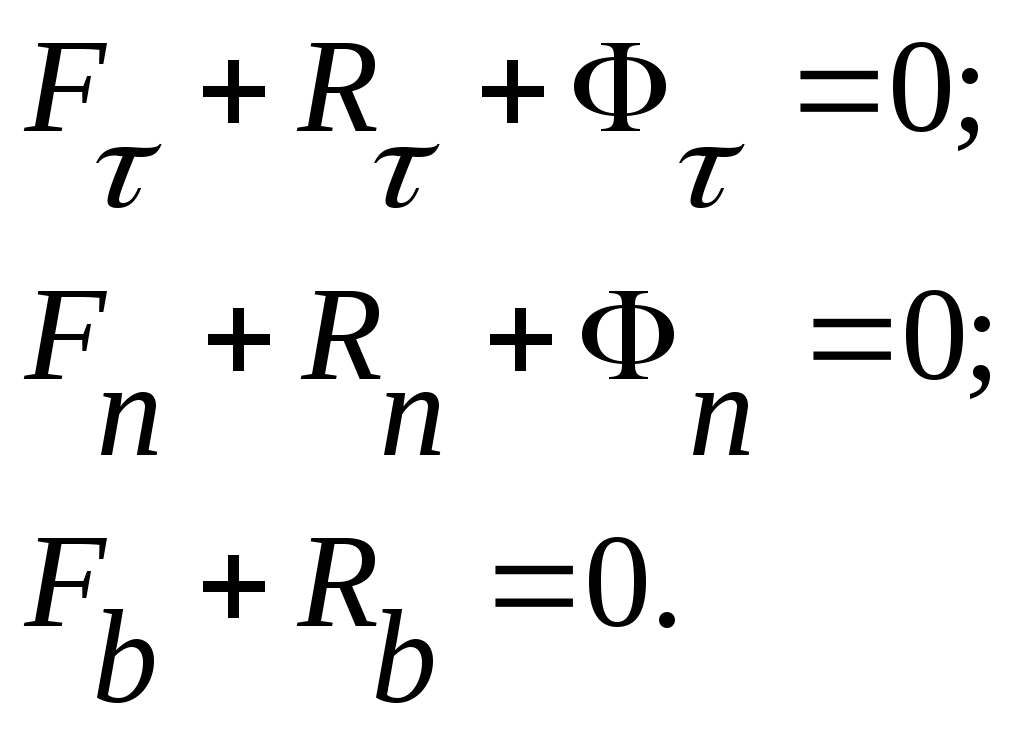   ; в проекциях на оси естественного трехгранника получаем: , где   .Представление основного уравнения динамики материальной точки в виде (2) следует рассматривать как прием, удобный для решения задач, например для определения сил взаимодействия и реакций связей. Пример. Определить силу, с которой груз 2 давит на упор 1 тележки (Рис.1), если масса груза 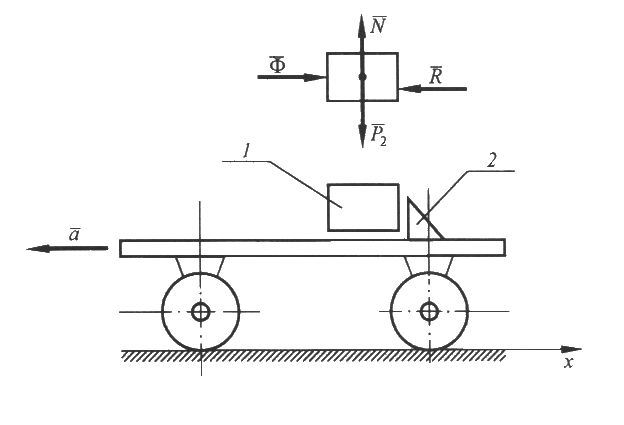 , а ускорение тележки  . Трением между грузом и тележкой пренебречь. Рис.1  Решение. К грузу приложена сила тяжести  , нормальная реакция  и реакция упора  . Добавляя в соответствии с принципом Даламбера силу инерции  груза, получаем уравновешенную систему сил ( ).Проецируя силы на ось Ох , находим:  . Рассмотрим механическую систему, состоящую из  материальных точек. Применяя принцип Даламбера к каждой точке системы, получаем:  , (4) где  и  - равнодействующие активных сил и реакций связей, приложенных к  - ой точке. Условие (4) можно представить в виде .Таким образом, для системы материальных точек принцип Даламбера формулируется следующим образом: при движении механической системы в любой момент времени приложенные к каждой точке системы активные силы и реакции связей вместе с силами инерции образуют систему сил, эквивалентную нулю. Суммируя левые части уравнений (4) по всем точкам системы, получаем:  . (5)Умножая каждое уравнение в (4) векторно слева на радиус-вектор  -ой точки и проссумировав их, имеем , или . (6)Из (5) и (6) следует, что равны нулю главный вектор и главный момент относительно произвольного центра О активных сил, реакций связей, приложенных ко всем точкам механической системы, и сил инерции. В проекциях на оси декартовой системы координат, начало которых совпадает с центром О, эти условия принимают вид известных уравнений равновесия произвольной пространственной системы сил: 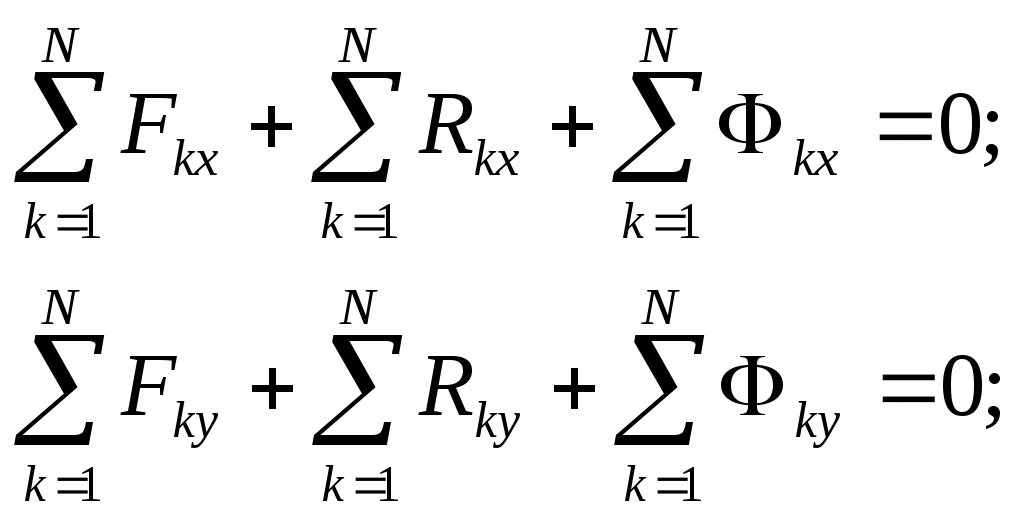 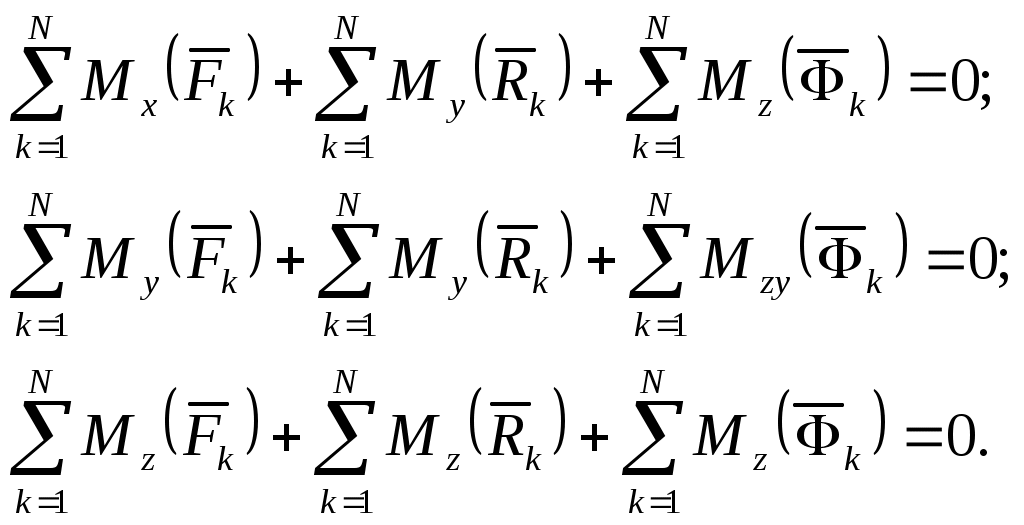 , (7) Если силы, приложенные к -ой точке системы, разложить не на активные и реакции связей, а на внешнюю и внутреннюю , то уравнение (4) примет вид .Так как главный вектор и главный момент относительно произвольного центра приведения внутренних сил системы равен нулю, то для (5) и (6) имеем соответственно:  . (8)Проецируя (8) на декартовые оси координат, получаем шесть уравнений равновесия сил, аналогичных уравнениям (7). Особенность этих уравнений состоит в том, что в них не входят внутренние силы. ГЛОССАРИЙ
Домашнее задание – рассмотреть сложное движение точки с применением понятия силы инерции См. Никитин Н.Н. Курс теоретической механики, Москва «Высшая школа»,1990 – 607с. |