!Конспект лекций Теоретичекая и прикладная механика. Лекция 1 Предмет теоретической механики. Кинематика точки
 Скачать 3.52 Mb. Скачать 3.52 Mb.
|
Цель лекции - изложить теорему об изменении момента количества движения для материальной точки и механической системыПлан лекцииМомент количества движения материальной точки и механической системы. Теорема об изменении момента количества движения КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Для характеристики движения материальной точки используют еще одну векторную меру движения – момент количества движения, или кинетический момент относительно центра. Моментом количества движения материальной точки массой mотносительно центра О называют векторную величину, равную векторному произведению радиус-вектора материальной точки, проведенного из этого центра, на количество движения точки (Рис.1): Проекции этого вектора: Рис.1 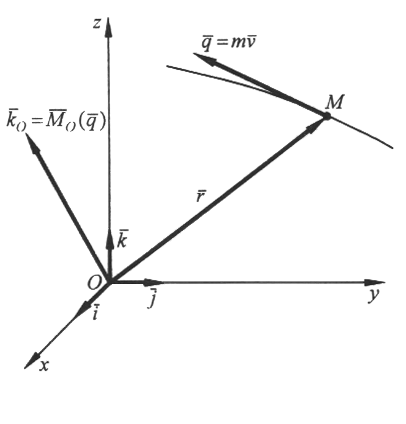 Так как 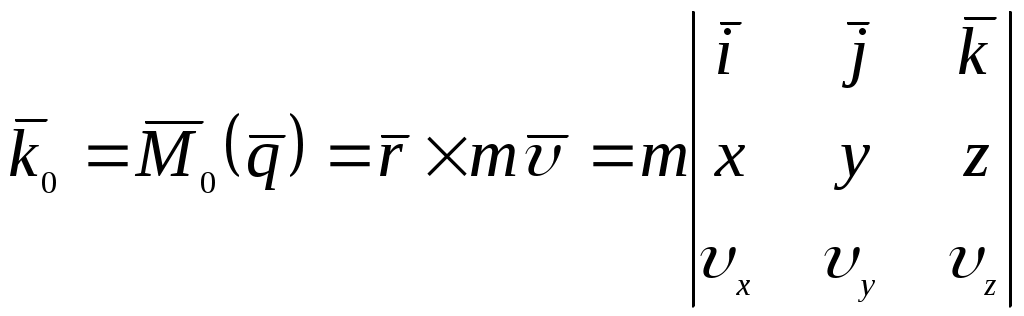 , ,то моменты количества движения материальной точки относительно осей координат имеют вид Единица измерения в системе СИ – кг ∙ м2/с . Главным моментом количества движения, или кинетическим моментом механической системы относительно центра О называют геометрическую сумму векторов моментов количеств движения материальных точек системы относительно того же центра О: Вектор главного момента количеств движения 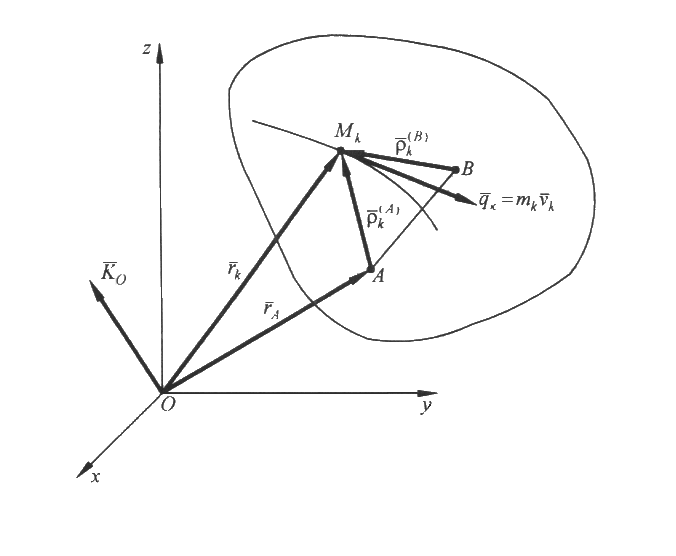 Рис.2 Проекции вектора (3) на оси координат: или Пусть твердое тело вращается вокруг неподвижной оси Oz с угловой скоростью 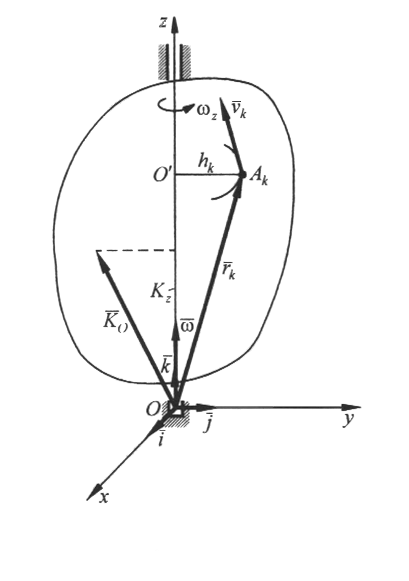 Рис.3 Проекции скорости точки Ак тела на касательную к траектории движения Знак Запишем уравнение движения материальной точки 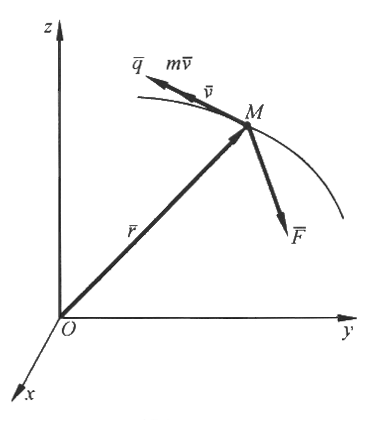 Рис.4 Преобразуем левую часть полученного уравнения: Но Эта формула выражает теорему об изменении момента количества движения материальной точки: первая производная по времени от момента количества движения точки относительно центра О равна моменту равнодействующей силы относительно того же центра О. Рассмотрим механическую систему, состоящую из Просуммировав (8) по всем точкам Преобразовав левую часть уравнения, получим: 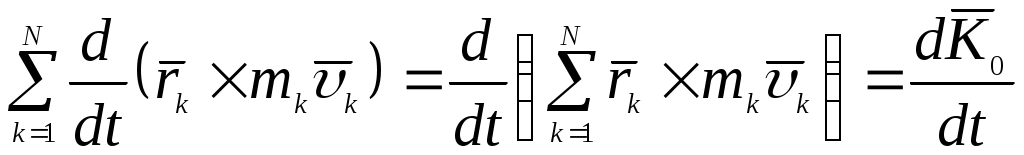 . . Здесь Главный момент внутренних сил Рис.5 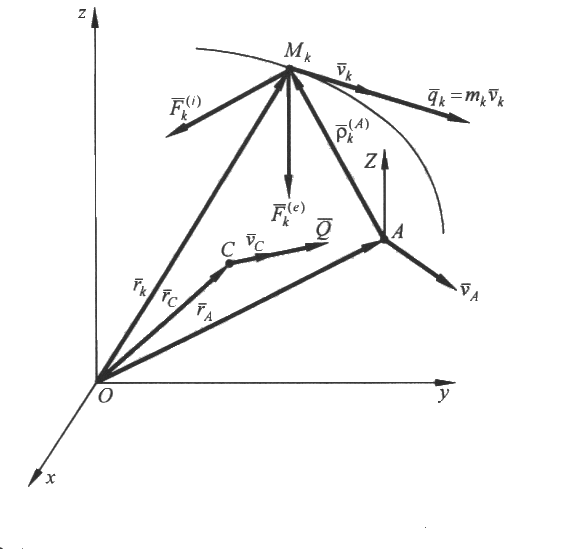 Окончательно имеем: Формула (11) формула выражает теорему об изменении главного момента количеств движения механической системы: первая производная от главного момента количеств движения механической системы относительно неподвижного центра О равен главному моменту внешних сил, приложенных к точкам системы, относительно того же центра. Теорема допускает первый интеграл (закон сохранения кинетического момента), если после интегрирования которого получаем: ГЛОССАРИЙ
Домашнее задание - Невесомый круглый диск радиусом R, расположенный в горизонтальной плоскости, вращается с угловой скоростью См. Никитин Н.Н. Курс теоретической механики, Москва,”Высшая школа”,1990 -607с. Лекция 14. Работа силы. Мощность Цель лекции – познакомить с мерой действия силы – работой и мощностью; рассмотреть некоторые примеры вычисления работы некоторых сил План лекции Элементарная работа силы; полная работа силы. Пример. Мощность силы 2. Работа силы в различных случаях движения твердого тела КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Элементарная работа силы. Пусть точка приложения силы Величина Таким образом, элементарная работа силы равна произведению элементарного переемещения на проекцию силы на это перемещение Поскольку Следовательно, элементарная работа силы 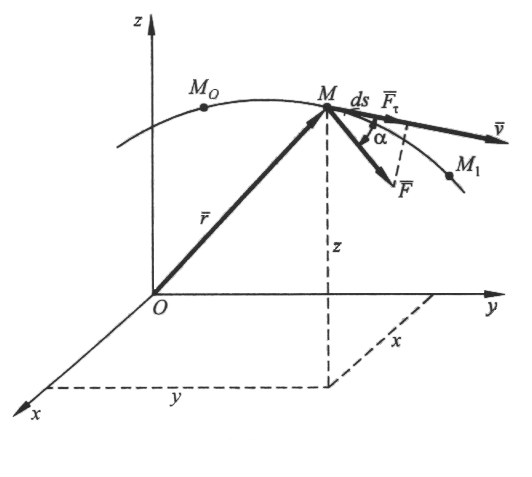 Рис.1 Так как , Таким образом, элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки ее приложения. В аналитической форме (4) будет иметь вид: Полная работа силы. Полную работу силы где Так как сумма (5) является интегральной суммой определения криволинейного интеграла, то 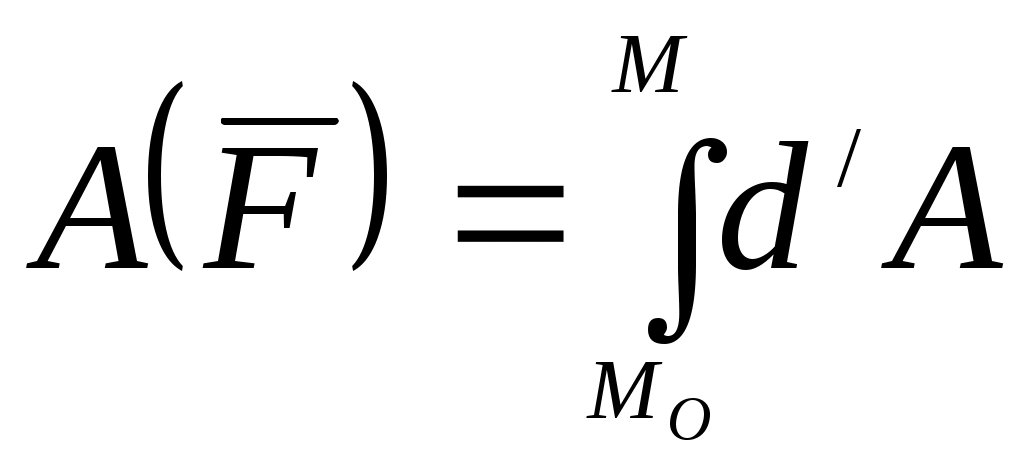 Используя различные формулы для определения элементарной работы, получаем: 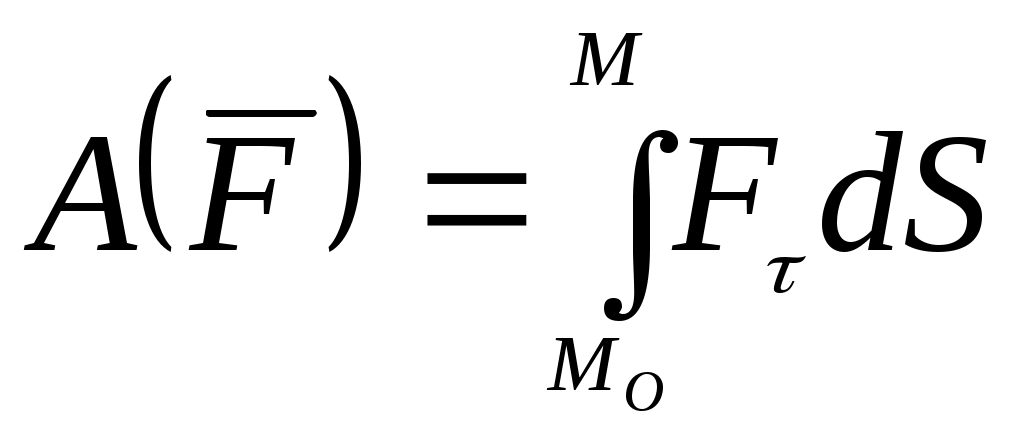 или или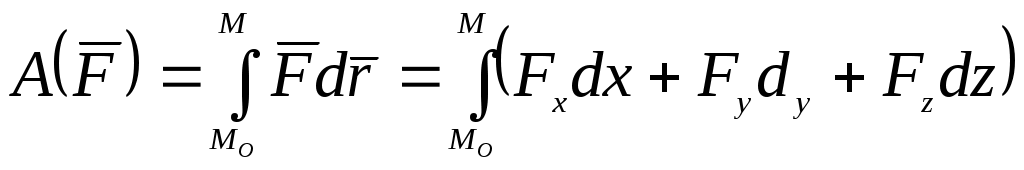 . .Если же сила является функцией времени, то, согласно (4), работа силы определяется выражением: Работа силы зависит от характера движения точки приложения силы. Например, если скорость точки приложения силы равна нулю, то Рассмотрим пример вычисления работы силы тяжести. Пусть на материальную точку М, на которую действует сила тяжести 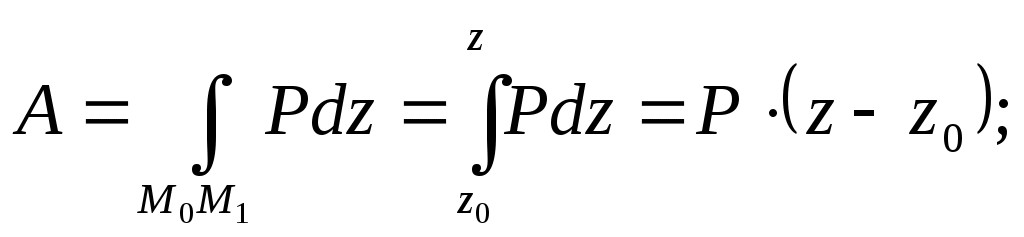 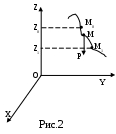 (7). (7). Обозначив h=z-z0 вертикальное перемещение, получим: или Следовательно, работа силы тяжести материальной точки равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ( при опускании точки работа положительная, при подъеме – отрицательная). Из формулы (8) следет, чторабота силы тяжести не зависит от формы траектории, по которой перемещается точка ее приложения. Единица измерения работы в системе СИ 1 джоуль |
