|
|
Термех. Билет 1 1
Билет 1
1.Статика-это раздел термех изуч.равновес.системы материал.точек и тв-ых тел, наход-ся под действием приложенных к ним сил.
Материал.точка-простейшая модель тела, имеющ.массу, но не имеющ.размеров.
Абсолют.тв.тело-тело конеч.размеров, расстоян. между любыми двумя точками, которого не измен.во время движ.
Сплошная деформируемая среда-заполн.колич.объем или неогранич.пространсво, расстоян.между точками такой среды могут меняться
Движение-измен.полож.точки или тв.тела в пространстве с течением времен под действием сил
Равновесие-рассматр.по отношению к некоторой неподвиж.системе координат
Сила-мера взаимодейст.точек и тела
Две основные задачи статики:
1.Заданы все силы,действующие на тело. Требуется определить, будет ли тело нах-ся в усл.равновесия
2.Тело нах-ся в усл.равновесия систем сил, действующих на тв.тело.треб-ся определ.силы входящ. в усл.равновесия
Силы имеют векторную природу, т.к. они опред-ся модулем,направлением и модулем действ.
2.Модуль ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, перпендикулярную оси переносного вращения; чтобы получить направление ускорения Кориолиса, следует вектор проекции относительной скорости спроецировать на пл-ть, перпендикуляр.вектору угловой скорости переносного вращат.движ.и повернуть проекцию на 90 в сторону переносного вращения.
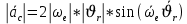
3.Основ.закон динамики-произвед.массы материал.точки на её ускор.,которые она получает под действием силы, равно модулю этой силы и направл.ускорения совпад.с направлен.вектора силы
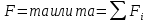
Основное ур-ие динамики: 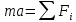
-cсоответ.векторному способу задания движ.точки 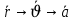
Билет 2
1.Сила- это мера взаимодействия точек или тел
Системой сил называется совокупность сил, приложенных к твердому телу. Система сил бывает: плоской (линии действия сил лежат в одной плоскости), пространственной (если лдс не лежит в одной плоскости), системой сходящихся сил (если лдс пересекаются в одной точке), системой параллельных сил (если лдс параллельны друг другу)
Две системы сил называют эквивалентными если одну систему сил, приложенных к свободному твердому телу можно заменить другой системой, не изменяя при этом состояние покоя или движения в кот находится тело
Если система сил эквивалента одной силе, то эта сила назыв равнодействующей силой данной системы сил.
Система сил назыв уравновешенной если в результате ее приложения к покоящемуся телу она не сообщает телу никакого движения.
2.Кориолисовым ускорением точки при сложном движении называется вектор 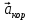 , характеризующий изменение во времени вектора относительной скорости в переносном движении точки и изменение вектора переносной скорости в относительном движении точки. , характеризующий изменение во времени вектора относительной скорости в переносном движении точки и изменение вектора переносной скорости в относительном движении точки. 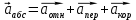 Вектор Вектор 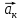 направлен так, что он перпендикулярен плоскости, образованной вектором угловой скорости движущегося в ту сторону откуда поворот от направлен так, что он перпендикулярен плоскости, образованной вектором угловой скорости движущегося в ту сторону откуда поворот от 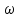 к к 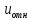 наблюдается происходящим против часовой стрелки. наблюдается происходящим против часовой стрелки.
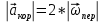 * *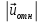 *sinα *sinα
3.Спроецировав уравнение 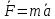 на декартовы оси координат, получим систему из трех уравнений на декартовы оси координат, получим систему из трех уравнений
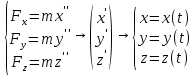
Билет 3
1. Аксиомы:
1) Действие на точку твердого тела нескольких сил равносильно действию одной равнодействующей силы, строящейся по правилу сложения векторов. (=теорема о трех непараллельных силах)
Следствие: силы, приложенные к точке твердого тела, складываются по правилу параллелограмма.
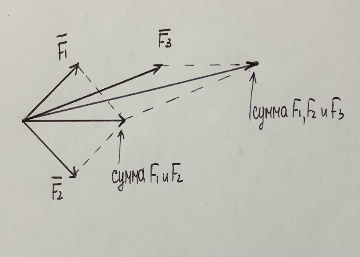
Закон параллелограмма сил: две силы, приложенные к твердому телу в одной точке, имеют равнодействующую силу, приложенную в той же точке и являющуюся диагональю параллелограмма, построенного на этих силах как на сторонах.
Вектор R называется геометрической суммой векторов F1 и F2
R=F1+F2
Модуль равнодействующей может быть вычислен с использованием теоремы косинусов по следующей формуле: 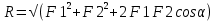 , где , где 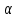 – угол между силами F1 и F2; – угол между силами F1 и F2;
2) Аксиома действия и противодействия: Две материальные точки действуют друг на друга с силами, равными по величине и противоположно направленными по прямой, соединяющей эти точки.
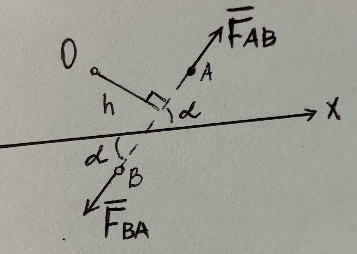
Fᴀᴃ = -Fᴃᴀ
Силы взаимодействия между телами и точками, образующими механическую систему, называются внутренними;
Сумма проекций внутренних сил на любую ось равна нулю;
Сумма моментов внутренних сил равна нулю относительно любого центра;
Для любой внутренней силы найдется другая, такая что
-Fᴃᴀ*cos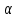 = Fᴀᴃ*cos = Fᴀᴃ*cos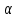
-Fᴃᴀ*hᴃᴀ = Fᴀᴃ*hᴀᴃ
3) Принцип пробивания: Действие на твердое тело системы сил не изменится, если добавить к этой системе или отбросить от нее две силы, равные по величине, направленные в противоположные стороны и лежащие на одной прямой.
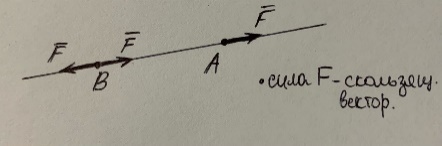
Следствие: Силу, действующую на точку твердого тела, можно переносить вдоль линии действия силы без изменения равновесия (т.е. сила является скользящим вектором).
4) Аксиома затвердевания: Равновесие геометрически изменяемой механической системы не изменится, если представить её затвердевшей
Принцип отвердевания: Равновесие дифференцируемого твёрдого тела, находящегося под действием данной системы сил, не нарушится, если тело считать абсолютно твёрдым.
Силы:
Активные – создают или способны создать движение твёрдого тела, например - сила веса; Пассивные – не создающие движение, но ограничивающие перемещение твёрдого тела, препятствующие перемещению. Например, сила натяжения нерастяжимой нити.
5) Аксиома освобождаемости от связей: Связи, наложенные на систему материальных точек, можно заменить силами реакций, действие которых эквивалентно действию связи. Когда пассивные силы не могут уравновесить действие активных сил, начинается движение. Какие-либо устройства, ограничивающие движение тел и материальных точек, называются связями.
Равновесие механической системы ни изменяется, если действие на неё связей заменить силами – реакциями связи.
Связи классифицируют по числу ограничений, накладываемых на движение материальных точек и твёрдых тел. Каждому из таких ограничений соответствует составляющая реакции связи.
Связи первого рода – направление реакции заранее известно.
Гладкая плоскость, стержень, нерастяжимой нить;
Связи второго рода – шарниры; Запрещает любые движения твёрдого тела.
Цилиндрический шарнир, сферический шарнир.
2. Теорема о сложении ускорений в сложном движении точки. (Теорема Кориолиса): Абсолютное ускорение точки при сложном движении равно геометрической сумме относительного, переносного ускорений и ускорение Кориолиса.
Относительное ускорение точки характеризует изменение относительной скорости в относительном движении;
Переносное ускорение точки характеризует изменение переносной скорости в переносном движении;
Ускорение Кориолиса характеризует изменение относительной скорости точки в переносном движении и переносной скорости точки в относительном движение; оно возникает вследствие взаимного влияния движений, в которых участвует точка.
3.
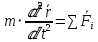
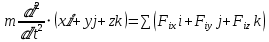
(Ox): 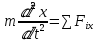 m m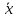 = =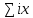
(Oy):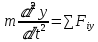 m m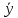 =∑iy =∑iy
(Oz):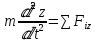 m m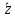 = ∑iz = ∑iz
Естественные уравнения движения материальной точки получаются проецированием векторного дифференциального уравнения движения на естественные (подвижные) оси координат.
Условия:
- траектория движения
- откуда началось движение
- шаг, как меняется координата
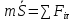
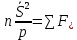 – естественные уравнения движения точки – естественные уравнения движения точки
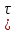 ): m ): m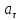 == ==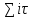
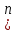 ): m ): m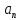 == ==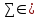
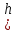 ): m*0== ): m*0==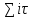
Билет 4
1. Какие6 либо силы, ограничивающие движение тел и мат. точек нзв связями. Равновесие механической системы не изменяется, если действие на нее связей заменить силами-реакциями связей. Все связи классифицируются по характеру действий. Связи классифицируются по числу ограничений, накладываемых на движение мат. точки и твердого тела. Каждому из таких ограничений соответствует составляющая реакции связи.
С вязи 1-го рода- направление реакции заранее вязи 1-го рода- направление реакции заранее
N
  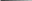  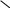   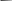
Гладкая (без трения) плоскость
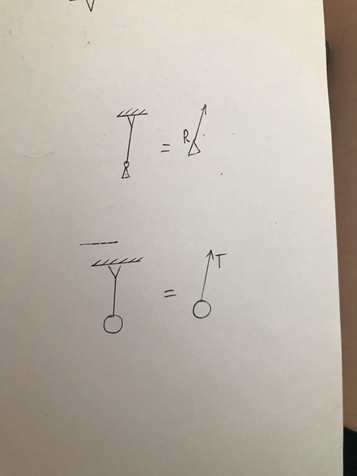
Стержень
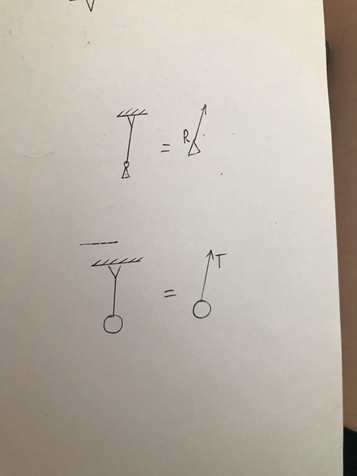
Нерастяжимая нить
Связи 2-го рода – шарниры (запрещают движение тв.тела)
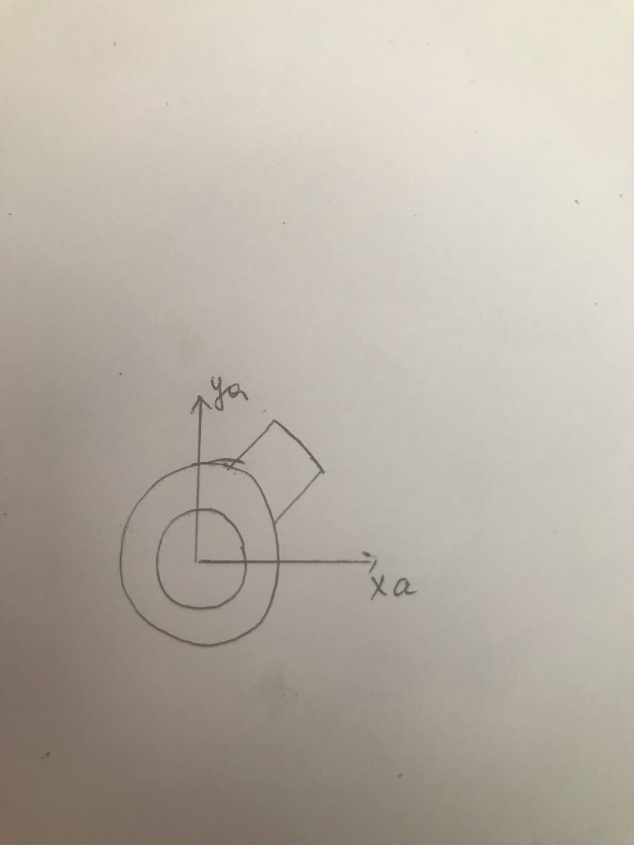
Цилиндрический шарнир
Связи 3-го рода (запрещает любые движения твердого тела)
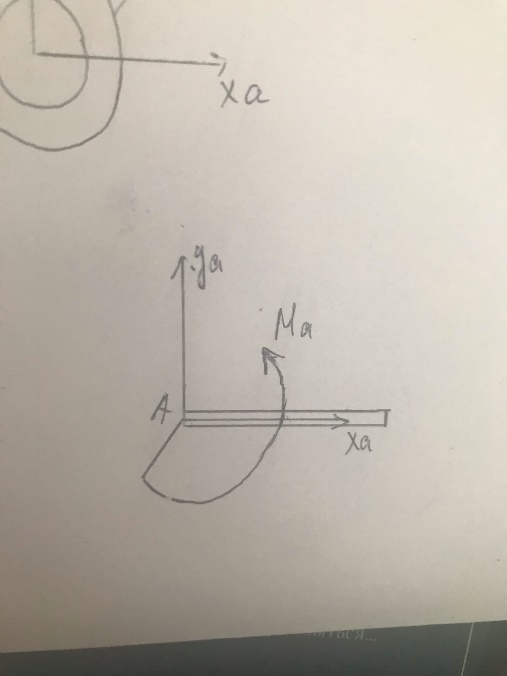
Плоская заделка- силы по условию задачи можно расположить в одной плоскости
Пространственная заделка- решение задачи производится при произвольном расположении сил в пространстве
Принцип освобождаемости: всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к телу.
2. Абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей
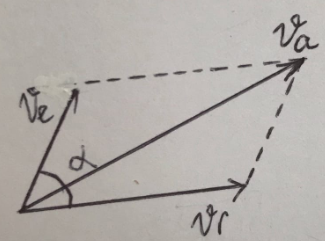
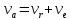 , ,
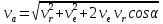 , где , где 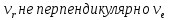
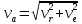 , где , где 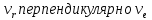
Относительным является прямолинейное движение по ребру треугольника
Переносным движением является вращательное движение вокруг неподвижного шарнира
3. Если на материальную точку действует сила, зависящая от времени R(t), то дифференциальное уравнение прямолинейного движения вдоль оси Ox имеет вид
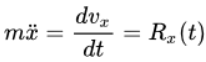
Билет 5
1. Пусть линии действия сил, действующих на тело, расположены в одной плоскости. Такую систему сил, как известно, называют плоской системой сил. можно считать, что силы приложены к самой плоскости, а плоскость жестко связана с телом. В качестве меры «поворотного действия» силы относительно некоторой точки (центра) в известной плоскости в механике вводится величина, называемая алгебраическим моментом силы, которая однозначно определяет и направление поворота, и величину поворотного действия силы.
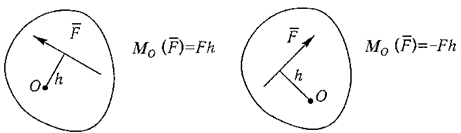
Правило знаков принимается следующее: если плоскость, образованная вектором силы и точкой О, стремится повернуться под действием силы вокруг точки О против движения часовой стрелки, то следует брать знак плюс, если по движению часовой стрелки - то знак минус.
1.Момент силы не изменяется, если силу перемещать вдоль линии действия не меняя направления силы
2.Алгебраический момент силы =0, если линия действия силы проходит через центр O.
2.Сложным движением точки называется такое движение, при котором точка одновременно участвует в двух или нескольких движений. (сложное или абсолютное движение складывается из относительного и переносного движения)
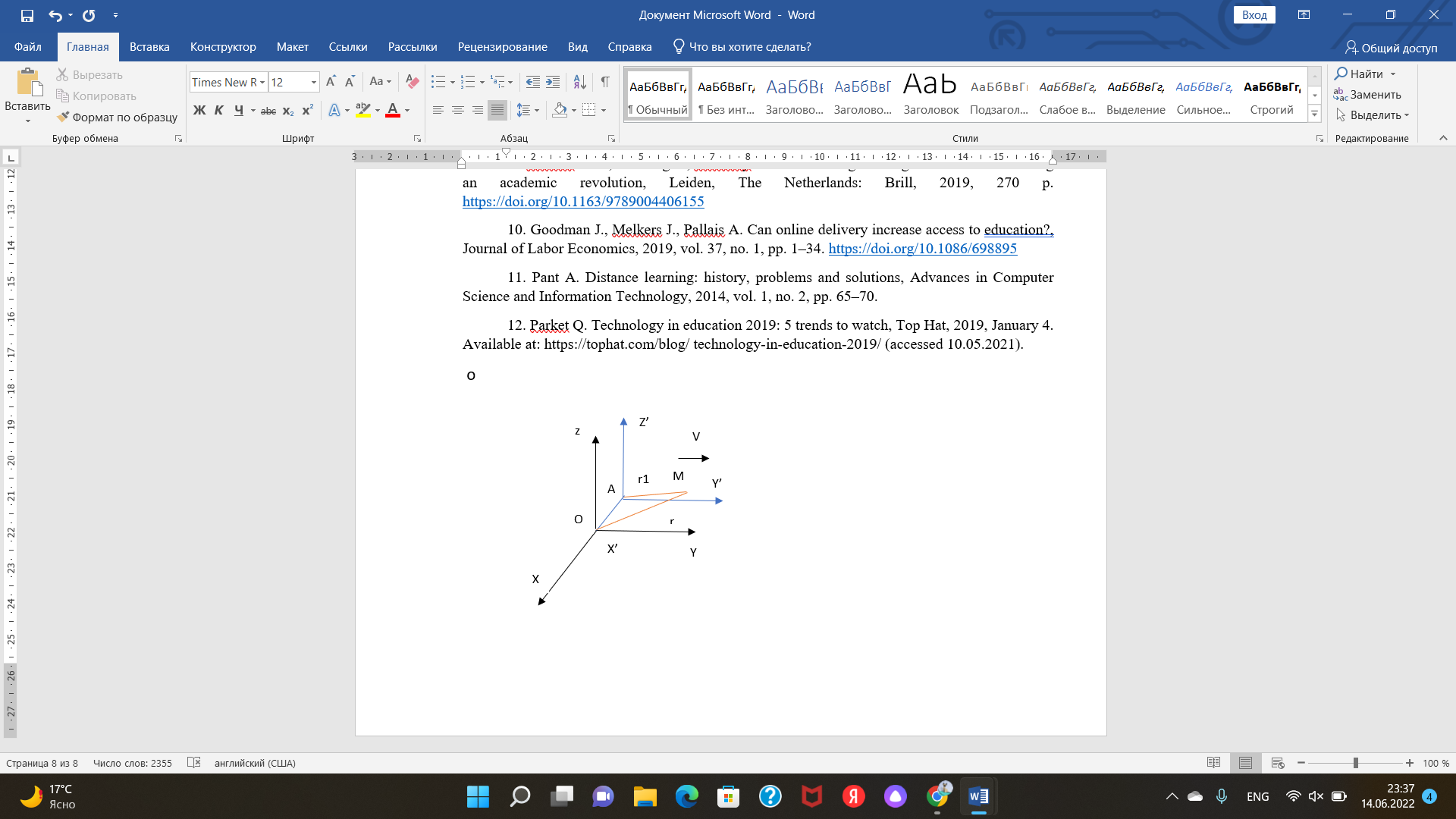
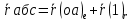
Абсол: Oxyz(неподв,глоб)
Относ: Ax’y’z’
Перенос: Ax’y’z’ в Oxyz
Абсолютным движением называется точки относительно неподвижной системы отсчета.
Относительным движением называется движение точки относительно подвижной системы отсчета.
Переносным движением называется движение подвижной системы отсчета вместе с точкой относительно неподвижной.
3.Заданы силы, под действием которых происходит движение. Требуется найти параметры движения(уравнение движения, траекторию)
Решение: в общем случае движение точки силы, действующей на точку является перемещением зависимости от времени, координат и скорости. Движение точки описывается системой трех диф.ур. второго порядка.
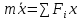
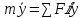
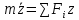
Интегрируем
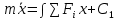
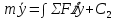
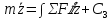
Интегрируем и делим на массу
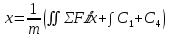
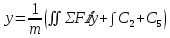
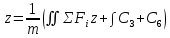
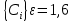
В результате интегрирования появляются 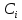 в количестве 6 штук. в количестве 6 штук.
Таким образом, под действием одной и той же системы сил материальная точка может совершать целый класс движений, опред. Начальным условием (начальное положение и начальная скорость)
Константы интегрирования будут опред. Из начальных усл. 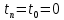
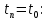
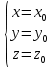 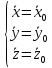 | |
|
|
 Скачать 5.41 Mb.
Скачать 5.41 Mb.