Термех. Билет 1 1
 Скачать 5.41 Mb. Скачать 5.41 Mb.
|
|
Билет 6 1. Вектором-моментом или просто моментом силы относительно центра(точки) является векторное произведение радиус-вектра точки приложения силы на саму силу 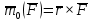 Свойства: Момент силы относительно центра зависит от выбора центра. Модуль момента силы относительно точки равняется удвоенной площади треугольника построенного на векторах. Момент силы относительно точки не изменяется при перенесении силы вдоль ее линии действия, поскольку неизменным остается плечо силы. Момент силы относительно центра (точки) равняется нулю, если : Сила равняется нулю (F=0) Плечо силы h=0, то есть линия действия силы проходит через центр 2. Свободным называют такое движение тела, при котором на его положение в пространстве не наложено никаких ограничений, то есть оно может перемещаться как угодно по отношению к системе отсчета O 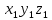 . По отношению к полюсу тело совершает сферическое движение. . По отношению к полюсу тело совершает сферическое движение. Вывод. Движение свободного тела раскладывается на поступательное вместе с полюсом и сферическое вокруг полюса. Положение тела определяют 6 параметров: 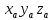 и углы Эйлера – и углы Эйлера –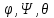 3. Прямая задача динамики Задано движение. Требуется определить силы, под действием котрых происходит заданное движение. Обратная задача динамики Заданы силы, под действием которых происходит движение. Требуется найти параметры движения. Начальными условиями называются ,пример t=0, 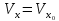 Билет 7 1. 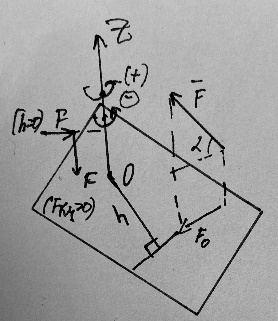 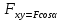 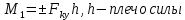 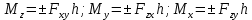 Свойства: Момент=0, если сила параллельна оси. В этом случае равна нулю проекция силы на пл-ть, перпенд. Оси Момент=0, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы Если ось и сила составляют одну пл-ть, то момент силы отн-но оси =0. В этом случае либо h=0, либо Fky=0  Осуществляется проецированием силы на пл-ть перпенд-ную этой оси и умножением величины полученного таким образом направленного отрезка на длину перпендикуляра, опущенного из точки пересечения оси на линию действия отрезка. Момент считается +, если набл. с конца оси поворота силы видится направленный против часовой стрелки (- наоборот) 2. Сферическим называется такое движение твердого тела, при котором во все время движения одна и та же точка твердого тела остается неподвижной. Остальные точки движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой. ! Число степеней свободы твердого тела при сферическом движении равно трём. 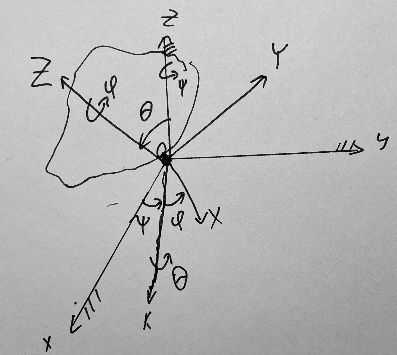 Углы Эйлера: Oxyz – неподвиж. система координат OXYZ – подвижная сист. коорд., жестко связанная с телом OK – линия узлов/пересечения пл-тей  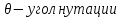 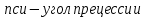 Уравнения вращения твердого тела вокруг неподвижной точки: 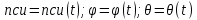 3. 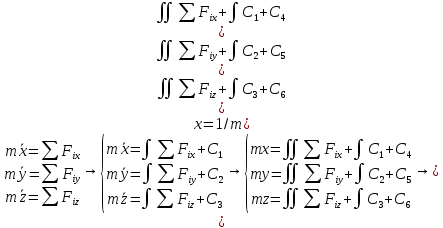 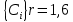 В результате интегрирования появл. Сi в количестве 6 штук. Константы интегрирования будут определяться из начальных условий: 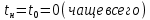 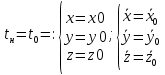 Билет 8 1. Момент силы относительно центра - вектор, перпендикулярный плоскости, образованной силой и центром Н 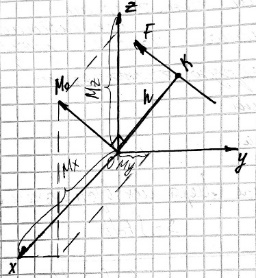 аправлен в сторону, с которой мыслимый поворот плоскости под действием силы видится происходящим против часовой стрелки аправлен в сторону, с которой мыслимый поворот плоскости под действием силы видится происходящим против часовой стрелки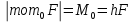 , h – плечо силы , h – плечо силы 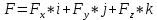 , ,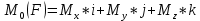 . .Проекция момента силы относительно центра на ось, содержащую этот центр, нзв моментом силы относительно оси 2. Поступательное движение твердого тела – движение в какой – либо системе отсчета, при котором любая прямая, состоящая из точек тела, остается параллельной самой себе Теорема: при поступательном движении все точки тела описывают одинаковые (траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения, то есть: 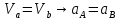 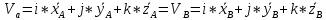 . .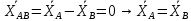 . . AB – произвольная прямая 3  . Естественные уравнения движения материальной точки – получаются проецированием векторного дифференциального уравнения движения на естественные (подвиж.) оси координат . Естественные уравнения движения материальной точки – получаются проецированием векторного дифференциального уравнения движения на естественные (подвиж.) оси координат 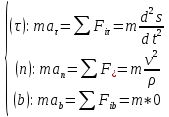 . .Билет 9 1. Пару сил представляют в виде двух сил, приложенных к твердому тел, равных по величине, и противоположно направленных. Расстояние между линиями действия сил называется плечо. Плоскостью в которой лежат силы нзв плоскостью пары. Суммарный момент сил сост-их пару одинаков относительно любого центра. Сумма проекций сил пары на любую ось=0. Поэтому действия пары сил на тело харак-ся только ее моментом модуль которого М=F*h Пара сил вызывает вращение, не имеет равнодействующей. Момент пары свободный вектор, он ┴ плоскости пары, направлен в ту сторону куда происходит вращение(против часовой+, по часовой-) Моментом пары нзв вектор равный векторному произведению 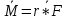 модуль которого равен произведению модуля одной из сил пары на ее плечо модуль которого равен произведению модуля одной из сил пары на ее плечо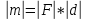 . Момент пары . Момент пары 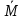 -свободный вектор, т.е его можно прикладывать в любой точке тела -свободный вектор, т.е его можно прикладывать в любой точке тела2. Если известен угол поворота или угловая скорость в зависимости от времени, то угловое ускорение определяем путем дифференцирования их по времени, т.е. У 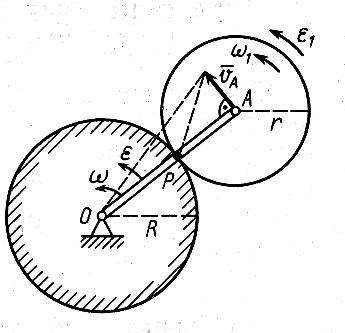 гловое ускорение тоже можно получить путем дифференцирования угловой скорости по времени. Угловую скорость можно найти: гловое ускорение тоже можно получить путем дифференцирования угловой скорости по времени. Угловую скорость можно найти:где А – точка плоской фигуры; Р – мгновенный центр скоростей. Дифференцируя по времени, получаем В тех случаях, когда АР постоянно, ; где Так, например, при качении колеса без скольжения по неподвижной прямой линии, если за точку А взять центр колеса О, то, учитывая, что он движется прямолинейно, получим При качении без скольжения одного колеса по неподвижному другому колесу Дифференцируя по времени, имеем + 3. Количество движения точки-мера мех. Дв, определяемая вектором равным произведению массы точки на вектор ее скорости Q=m*v(направлено по касательной к траектории дв-ия, как и скорость) Импуль силы-мера механ. Взимодействия, характ-щая передачу мех. Дв. Со стороны действующих на точку сил за данный промежуток времени 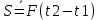 В проекциях на координаты: Ox:Sx= В проекциях на координаты: Ox:Sx=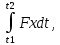 Oy:Sy= Oy:Sy=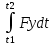 , Oz: Sz= , Oz: Sz=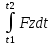 ; Sx=Fx(t2-t1) ; Sx=Fx(t2-t1)Импульс с равнодействующей –равен геометрической сумме импульсов приложенных к точке сил за один и тот же промежуток времени. 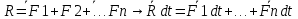 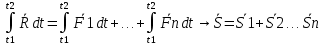 | Билет 10 1. Сложение двух параллельных сил, напр-х в одну сторону. Равнодействующая с-мы двух парал. сил, напр-ых в одну сторону, равняется по модулю сумме модулей составляющих сил, параллельна им и направлена в том же направлении. 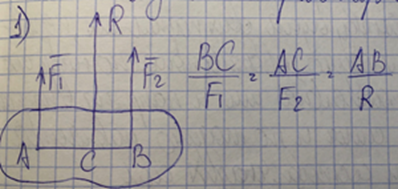 Сложение двух параллельных сил, напр-ых в разные стороны. Равнодействующая двух параллельных, неравных по модулю, противонапраленных сил параллельна им и напр-на в напр-ии большей силы и по модулю равняется разности составляющих сил: R=F1-F2 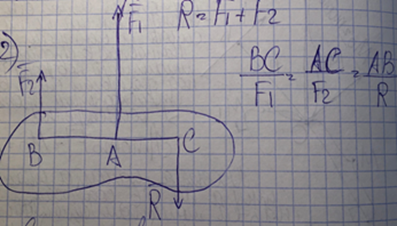 2. Ускорение любой точки плоской фигуры есть геометрическая сумма ускорения полюса и центрострем. и вращ. ускорений при вращении точки вокруг полюса. 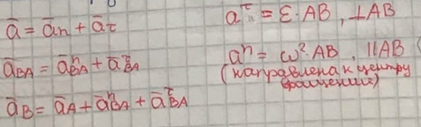 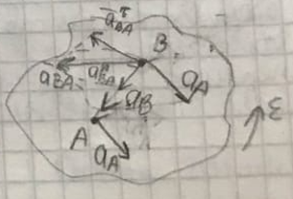 С1: проекция ускорения 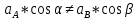 C2: для опр-я уск-я точки, лежащей на отрезке АВ, необх-мо соединить концы ускор. т.А и т.В и поделить полученный отрезок в той же пропорции, в которой т.С делит отрезок АВ. Соединив А и В получим уск-е т.С МЦУ – это точка Q уск-е которой в данный момент времени равно нулю Утверждение: для непоступ. дв-я МЦУ сущ-ет и единственен 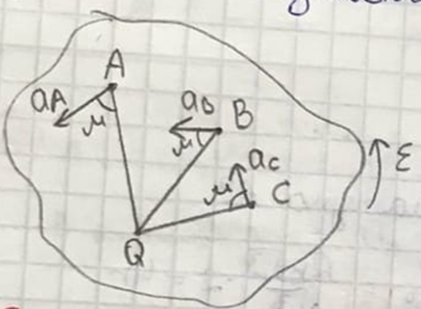 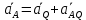 »» »» 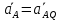 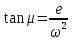 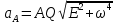 »» »» 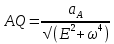 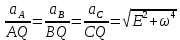 3. Импульс силы – мера мех. взаим-я, характеризующая передачу мех. дв. со стороны действующих на точку сил за данный промежуток времени 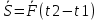 Кол-во дв-я точки – мера мех. дв., определяемая вектором, равным произв-ю массы точки на вектор её ск-ти 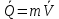 Единицей измерения импульса силы, как и кол-ва движения, является в СИ – 1 кг*м/с, а в системе МКГСС – 1 кГ*с Билет 11 1. Силу, не изменяя оказываемого ею действия на твёрдое тело, можно переносить параллельно самой себе в любую точку твердого тела (центр приведения), добавляя при этом пару сил, момент которых равен моменту заданной силы относительно новой точки ее приложения. 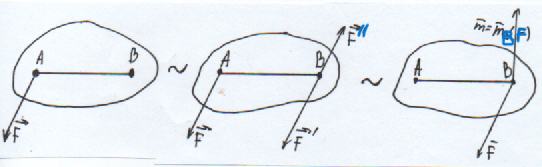 2. МЦС-это точка, принадлежащая плоскости или самой плоской фигуре, скорость которой в данный момент равна нулю. Способы определения МЦС: 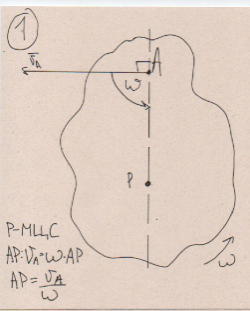 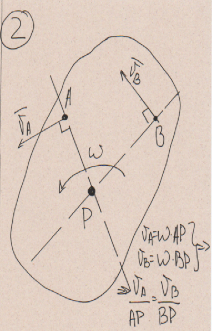 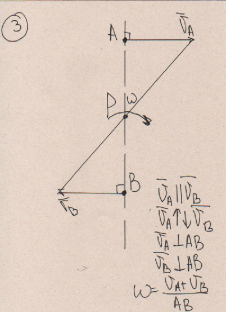 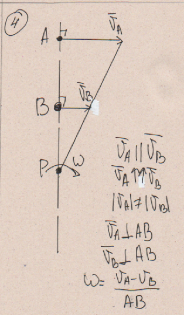 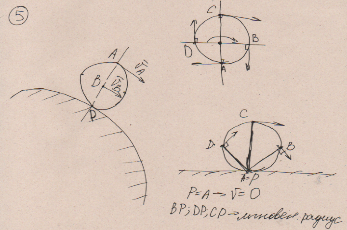 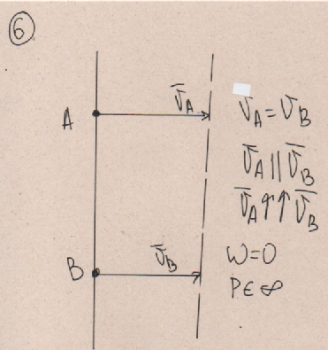  3. Интегрируя обе части d(mv)=Fdt в пределах от нуля до t , имеем mv ̅-mv ̅0=s ̅ где v ̅ - скорость точки в момент t ; v0 - скорость при t = 0; S - импульс силы за время t. Выражение в форме (3) часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени. Билет 12 1. Алгебраический момент силы 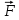 относительно точки О равен взятому с соответствующим знаком произведению. относительно точки О равен взятому с соответствующим знаком произведению. 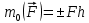 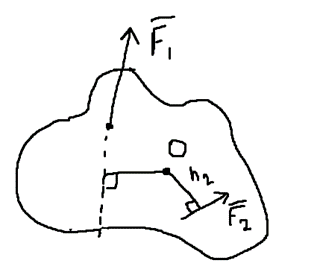 1.)Момент силы относительно центра не меняется при переносе силы вдоль линии её действия в любую точку. 2.)Если линия действия системы сил проходит через центр О (h=0), то момент силы относительно О равен 0. 3.)Для плоской системы сил при вычислении моментов сил относительно точки (центра), находящейся в той же плоскости, пользуются понятием алгебраического момента силы относительно точки. Момент считается +, если сила стремится повернуть вокруг точки О против хода часовой стрелки, и – по ходу часовой стрелки. 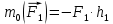 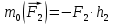 Вектором-моментом или просто моментом силы относительно центра (точки) является векторное произведение радиус-вектора точки приложения силы на саму силу. 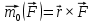 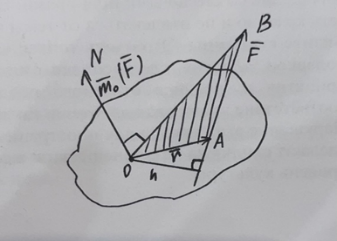 Теорема о приведении системы сил: любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру заменяется одной силой, равной главному вектору системы сил и приложенной в центре приведения, и одной парой с моментом равным главному моменту системы сил относительно данного центра. Главным вектором системы сил называется вектор R, равный векторной сумме этих сил: R = 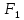 + + 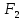 + ... + + ... + 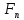 = =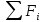 . .Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил. Главным моментом системы сил относительно центра O называется вектор L, равный сумме векторных моментов этих сил относительно точки О: L = 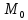 ( (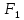 ) + ) + 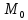 ( (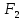 ) + ... + ) + ... + 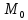 ( (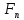 ) = ) = 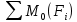 Вектор R не зависит от выбора центра, а вектор L при изменении положения центра может в общем случае изменяться. Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом L плоской системы сил относительно центра, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра, Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами. |
