Термех. Билет 1 1
 Скачать 5.41 Mb. Скачать 5.41 Mb.
|
|
2. 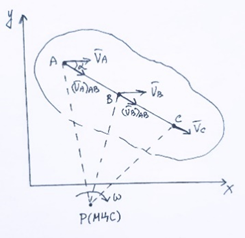 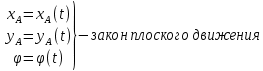 АВ – неизменна 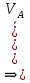 ; A и V опр-ся аналогично при поступ. и вращ. движении. ; A и V опр-ся аналогично при поступ. и вращ. движении.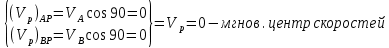 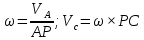 Поле скоростей аналогично вращательному движению,  Если перпендикуляры не пересекаются, то поле скоростей аналогично поступательному движению 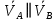 , поэтому , поэтому 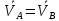 (в данный момент времени). (в данный момент времени).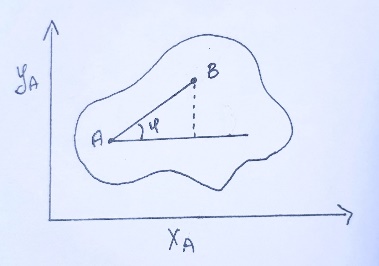 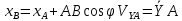 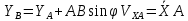 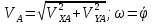 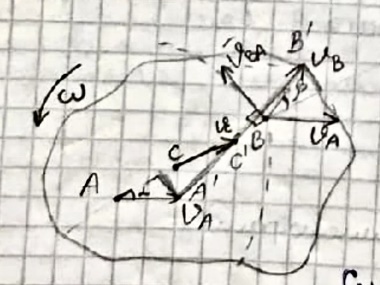 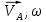 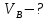 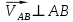 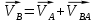 Следствие 1: 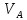 cos cos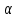 = =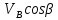 Следствие 2: Для определения 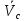 , которая делит отрезок АВ в известных пропорциях, , которая делит отрезок АВ в известных пропорциях, 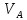 и и 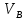 известны, необходимо воспользоваться алгоритмом. Построим отрезок известны, необходимо воспользоваться алгоритмом. Построим отрезок 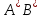 соединим концы векторов скоростей т. А, В и разделим соединим концы векторов скоростей т. А, В и разделим 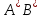 т. т. 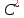 в тех же пропорциях в которых т.С дети отрезок АВ. Соединив С и в тех же пропорциях в которых т.С дети отрезок АВ. Соединив С и 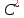 мы получим вектор скорости т.С мы получим вектор скорости т.С3.Элементарная работа силы Основным понятием настоящего раздела является элементарная работа силы. Пусть материальная точка движется произвольным образом в пространстве под действием силы F и за время dt совершает элементарное перемещение dr. Элементарной работой силы F на перемещении dr называется скалярное произведение силы на элемент перемещения. Физически элементарная работа характеризует суммарное действие силы на точку при ее перемещении на пути dr. Обозначая элементарную работу силы через 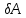 , имеем: , имеем: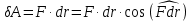 Произведение 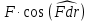 — — 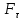 представляет проекцию вектора силы на касательную к траектории. Таким образом, можно сказать, что работу производит лишь касательная составляющая силы. Если сила направлена по нормали к траектории, то представляет проекцию вектора силы на касательную к траектории. Таким образом, можно сказать, что работу производит лишь касательная составляющая силы. Если сила направлена по нормали к траектории, то 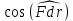 = 0 и работа равна нулю. Если сила образует тупой угол с направлением движения точки, то работа будет отрицательной. Итак, работа является скалярной алгебраической величиной. = 0 и работа равна нулю. Если сила образует тупой угол с направлением движения точки, то работа будет отрицательной. Итак, работа является скалярной алгебраической величиной.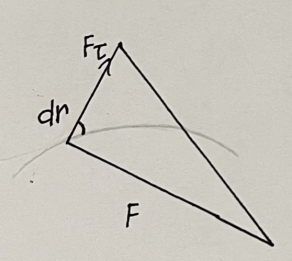 Различные формы записи элементарной работы силы Элементарное перемещение dr через вектор скорости можно представить в виде: dr=Vdt Тогда элементарная работа силы записывается так: 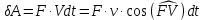 Если дугу траектории отсчитывать в сторону движения, то 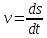 В элементарная работа может быть представлена в виде: 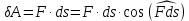 где ds— длина элемента траектории точки, ds — элементарный вектор, направленный вдоль траектории. Запишем элементарную работу силы через проекции силы F на оси координат 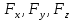 и ипроекции элементарного перемещения dr на оси координат dx, dy, dz. В силу свойства скалярного произведения будем иметь: 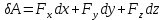 Переходя в последнем выражении к проекциям вектора скорости 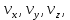 запишем: запишем: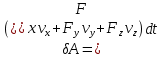 Работа силы на конечном пути Пусть точка М, находящаяся под действием силы F, перемещается по своей траектории из положения А в положение В. Впишем в дугу АВ ломаную, состоящую из n отрезков 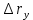 ( (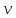 =1, ..., n), и вычислим работу силы F на каждом таком отрезке. Предполагая, что на каждом таком отрезке =1, ..., n), и вычислим работу силы F на каждом таком отрезке. Предполагая, что на каждом таком отрезке 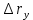 сила сила 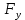 постоянна, ее работа будет постоянна, ее работа будет 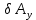 = = 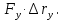 Сложив затем полученные работы и перейдя к пределу в предположении, что длины | Сложив затем полученные работы и перейдя к пределу в предположении, что длины | 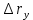 | стремятся к нулю, получим: | стремятся к нулю, получим:Билет 13 1. Произвольную систему сил, действ-ю на твердое тело, можно заменить эквивалентной системой, состоящей из силы и пары сил. Сила равна главному вектору сис. сил и приложена в произвольно выбранной точке (центре приведения), момент пары равен главному моменту сис. сил относительно этой точки. 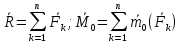 По инвариантам статики можно судить о возможных частных случаях приведения исходных систем сил. 1) 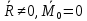 Система сил приводится к одной силе – равнодействующей, при этом линия действия равнодействующей проходит через центр приведения. Система сил приводится к одной силе – равнодействующей, при этом линия действия равнодействующей проходит через центр приведения.2) 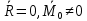 Исходную систему сил можно заменить двумя силами, образующими пару сил. Исходную систему сил можно заменить двумя силами, образующими пару сил.3) 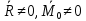 Система сил приводится к силе и паре. Система сил приводится к силе и паре.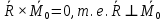 – пара и сила лежат в одной плоскости. – пара и сила лежат в одной плоскости.Выбирая силы, составляющие пару 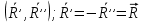 , находим ее плечо , находим ее плечо 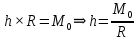 . .2. Плоское движение тв. тела представляется движением плоского сечения этого тела по неподвижной пл-ти. 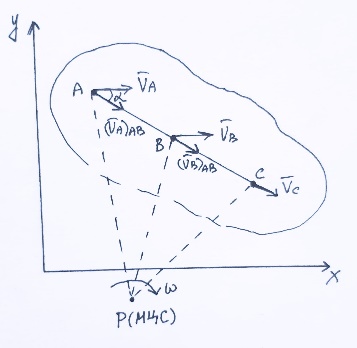 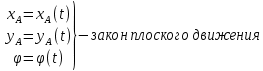 АВ – неизменна 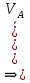 ; A и V опр-ся аналогично при поступ. и вращ. движении. ; A и V опр-ся аналогично при поступ. и вращ. движении.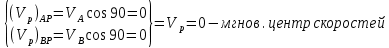 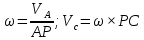 Поле скоростей аналогично вращательному движению, 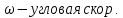 Если перпендикуляры не пересекаются, то поле скоростей аналогично поступательному движению 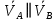 , поэтому , поэтому 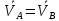 (в данный момент времени). (в данный момент времени).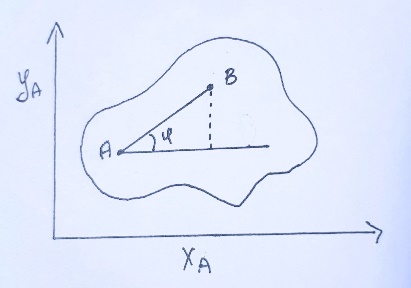 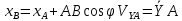 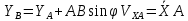 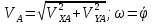 3. Работа силы тяжести не зависит от вида траектории и равна произведению силы тяжести на разность высот. 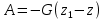 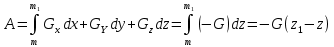 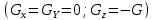 Если перемещение и направление силы тяжести соноправлены, то 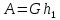 . . Работа линейной силы упругости при перемещении из состояния равновесия: 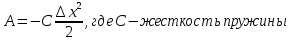 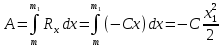 Билет 14 1. Систему сил называют сходящейся, если линии действия сил пересекаются в одной точке. Способы задания и сложения сил: 1)геометрический(работа с векторами) 2)аналитический(работа с проекциями сил) Рассмотрим сложение сходящихся сил, заданное геометрическим способом. 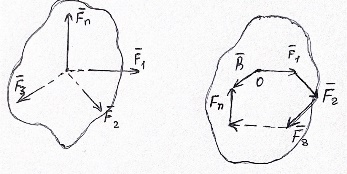 R=0 (замкнутый) силовой многоугольник Если имеем систему сходящихся сил, то главный вектор можно определить путем последовательного сложения сил по правилу параллелограмма или силового многоугольника. Это положение выражает усилие равновесия сходящейся системы сил в геометрической форме. Уравнение равновесия: 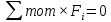 В такой системе сил их линии действия пересекаются в одной точке. Для равновесия тела, находящегося по действием сходящейся системы, необходимо и достаточно чтобы выполнялось одно геометрическое условие равновесия R=0, которое эквивалентно 3-м аналитическим условиям равновесия 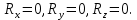 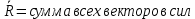 2. Чтобы найти выражения для векторов 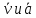 , проведем из т.О радиус-вектор , проведем из т.О радиус-вектор 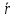 точки М. Тогда точки М. Тогда 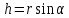 и и 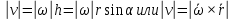 Таким образом, модуль векторного произведения 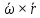 равен модулю скорости т.М. Направление векторов равен модулю скорости т.М. Направление векторов 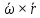 и и 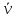 тоже совпадают и размерности их одинаковы. Следовательно тоже совпадают и размерности их одинаковы. Следовательно 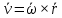 , т.е. вектор скорости любой точки равен векторному произведению угловой скорости тела на радиус-вектор этой точки. , т.е. вектор скорости любой точки равен векторному произведению угловой скорости тела на радиус-вектор этой точки.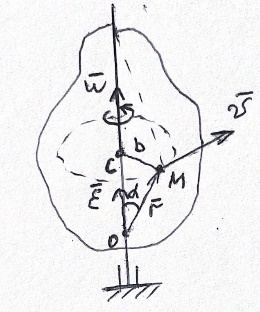 Беря от обеих частей равенства производные по времени, получим 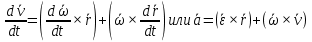 Данная формула определяет вектор ускорения любой точки вращающегося тела. Вектор 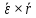 направлен, как и вектор направлен, как и вектор 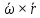 , т.е по касательной к траектории т.М. Вектор , т.е по касательной к траектории т.М. Вектор 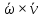 направлен вдоль МС, а направлен вдоль МС, а 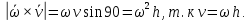 Заключаем, что Заключаем, что 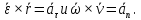 3. Кинетической энергией материальной точки называется скалярная величина, которая равняется половине произведения массы точки на квадрат ее скорости. Кинетическая энергия: характеризует и поступательное, и вращательное движения; не зависит от направления движения точек системы и не характеризует изменение этих направлений; характеризует действие и внутренних, и внешних сил. для материальной точки массой m, движущейся под действием силы 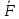 , основной закон динамики можно представить в виде: , основной закон динамики можно представить в виде: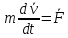 Умножая обе части этого соотношения скалярно на дифференциал радиуса-вектора точки d 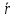 , имеем , имеем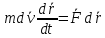 или или 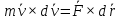 где 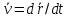 — скорость точки. — скорость точки.Учитывая, что 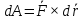 — элементарная работа, получаем — элементарная работа, получаем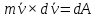 Так как 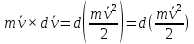 то окончательно 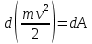 Данная формула выражает теорему об изменении кинетической энергии для точки в дифференциальной форме: дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку. Если обе части разделить на dt и учесть, что 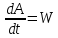 —мощность, то теорему можно также выразить в виде —мощность, то теорему можно также выразить в виде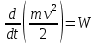 Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке. Интегрируя обе части от точки 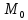 до точки M получаем теорему об изменении кинетической энергии точки в конечной форме: до точки M получаем теорему об изменении кинетической энергии точки в конечной форме: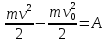 т. е. изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на том же перемещении. Билет 15 1. Произвольной плоской системой сил называется совокупность сил, линии действия которых лежат в одной плоскости. 1) 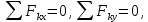 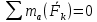 (подходит для жесткой заделки) (подходит для жесткой заделки)2) 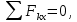 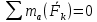 , , 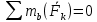 (для шарнирной заделки) (для шарнирной заделки)3) 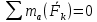 , , 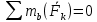 , , 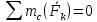 (т. А,B и C не лежат на одной прямой) (т. А,B и C не лежат на одной прямой)2. Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость 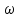 и углевое ускорение и углевое ускорение 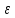 . .Если за промежуток времени 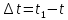 тело совершает поворот на угол тело совершает поворот на угол 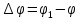 , то численно средней угловой скоростью тела за этот период времени будет , то численно средней угловой скоростью тела за этот период времени будет 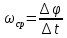 , при , при 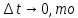 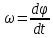 или или 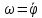 (1) (1)Угловую скорость тела можно изобразить в виде вектора 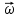 , модуль которого равен | , модуль которого равен |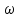 | и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки. Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой. оси. | и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки. Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой. оси. Угловое ускорение характеризует изменение с течением времени угловой скорости тела. Если за промежуток времени 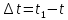 угловая скорость тела изменяется на величину угловая скорость тела изменяется на величину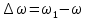 , то числовое значение среднего углового ускорения тела а этот промежуток времени будет равно , то числовое значение среднего углового ускорения тела а этот промежуток времени будет равно 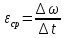 , при , при 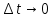 найдём, одновременно учитывая равенство (1), тогда: найдём, одновременно учитывая равенство (1), тогда: 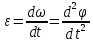 или или 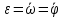 Угловое ускорение тела (по аналогии с угловой скоростью) можно также изобразить в виде вектора 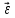 , направленного вдоль оси вращения. При этом , направленного вдоль оси вращения. При этом 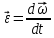 Направление 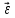 совпадает с направлением совпадает с направлением 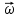 , когда тело вращается ускоренно (рис. а), и противоположно , когда тело вращается ускоренно (рис. а), и противоположно 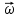 при замедленном вращении (рис. б). при замедленном вращении (рис. б).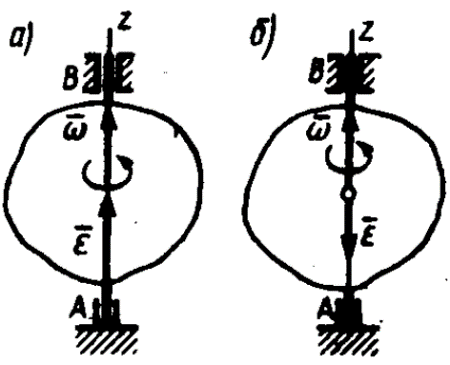 |
