Термех. Билет 1 1
 Скачать 5.41 Mb. Скачать 5.41 Mb.
|
|
3. 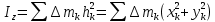 М 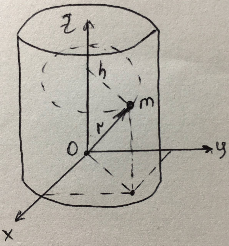 омент инерции тв.тела относ.оси равен сумме произведений массы каждой точки на квадрат расстояния от этой точки до оси. омент инерции тв.тела относ.оси равен сумме произведений массы каждой точки на квадрат расстояния от этой точки до оси.При переходе от дискретной малой массы к бесконечно малой массе точки предел такой суммы опр интегралом 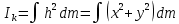 – осевой момент инерции тв.тела. – осевой момент инерции тв.тела. 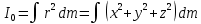 - полярный момент инерции - полярный момент инерцииРазмерность определяется из соотношения 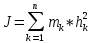 - [кг* - [кг*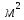 ] ]J – осевой момент инерции, 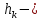 расстояние от точки k до оси. расстояние от точки k до оси.Билет 16 1.Плоской системой параллельных сил – линии действия всех сил лежащих в одной плоскости и параллельных друг другу. Пространственная система параллельных сил – линии действия сил параллельны друг другу, но не лежат в одной плоскости. Уравнения равновесия . Плоской система параллельных сил: 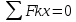 , , 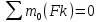 Пространственная система параллельных сил: 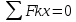 , , 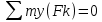 , , 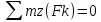 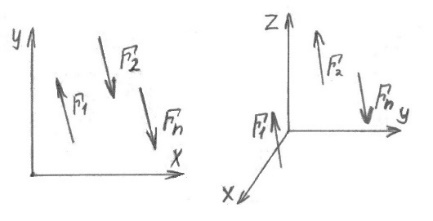 2. 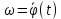 – угловая скорость – угловая скорость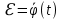 – угловое ускорение – угловое ускорение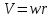 – скорость точки вращающегося тела (линейная скорость) – скорость точки вращающегося тела (линейная скорость)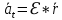 - векторное касательное ускорение - векторное касательное ускорение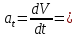 – касательное ускорение – касательное ускорение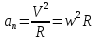 – нормальное ускорение – нормальное ускорение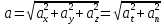 – ускорение точки вращающегося тела – ускорение точки вращающегося тела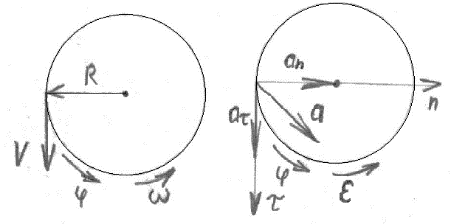 3.Радиус инерции твердого тела относительно некоторой оси – это расстояние от оси до точки, в которой надо сконцентрировать массу тела, чтобы момент инерции этой точки относительно оси был равен моменту инерции тела. Момент инерции относительно произвольной оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. 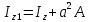 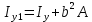 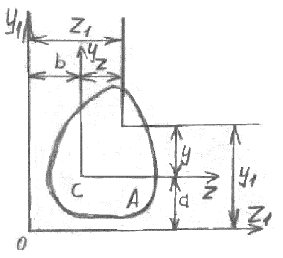 Билет 17 1. Система сил называется пространственной, если силы не лежат в одной плоскости и линии действия сил не пересекаются в одной точке. Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю. 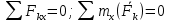 ; ; 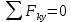 ; ; 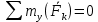 ; ;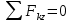 ; ; 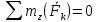 ; ;2. Угловая скорость- вектор, равный по величине производной от угла поворота по времени и направленный вдоль оси вращения. 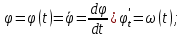 Ед. измерения [ 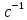 ] ]Угловое ускорение – вектор, равный по величине производной от вектора угловой скорости по времени. 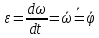 Ед.измерения[ 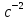 ] ]Вращательное движение тв.тела- движение в какой- либо системе отсчета, при котором существует проведенная в теле прямая, точки которой остаются неподвижными( ось вращения). Вводятся пересекающиеся плоскости: неподвижная, жестко связанная, фиксированная в твердом теле. Частные случаи вращательного движения твердого тела. 1.Равномерное вращение 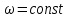 2.Равнопеременное вращение 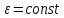 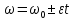 ; ; 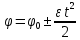 а) если 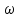 и и 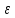 сонапрвлены, движение ускоренное сонапрвлены, движение ускоренное б) если 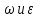 противоположно направлены, движение замедленное противоположно направлены, движение замедленное3.момент инерции однородного стержня dm=pAdx- элементарная масса 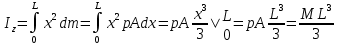 ; ; 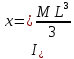 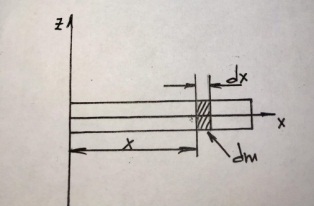 Для вычисления момента инерции относительно центральной оси( проходящей через центр тяжести) достаточно изменить расположение оси и задать предел интегрирования (-L/2; L/2). 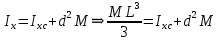 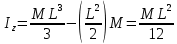 момент инерции диска 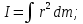 dm= dm=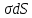 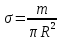 ; dS=2 ; dS=2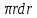 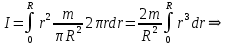 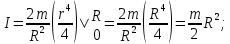  момент инерции однородного сплошного цилиндрического катка dV=2 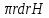 - элементарный объём - элементарный объём dm= 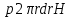 - элементарная масса - элементарная масса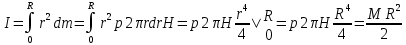 Для вычисления момента инерции пустотелого ( толстого) цилиндра достаточно задать пределы интегрирования от 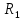 до до 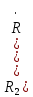 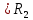 ) )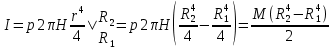 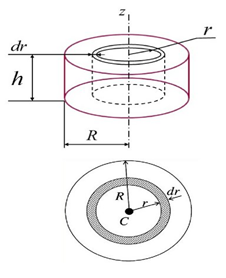 Билет 18 1. Системы тел, свободно опирающихся друг на друга или соединенных между собой какими-нибудь связями и находящейся под действием произвольной плоской системы сил или плоской системы параллельных сил. Такую систему сил назыв. сочлененной системой. После отбрасывания внешних связей (связи, скрепляющие сочлененную систему с не входящими в нее телами, назыв. внешними, в отличие от внутренних связей, соединяющих м/у собой тела данной сочлененной системы) сочлененная система не остается жесткой. Метод расчленения: Для сочлененной системы из «n» тел, на каждое из которых действует произвольная плоская система сил, методом расчленения можно составить 3n независимых уравнений равновесия, позволяющих найти 3n неизвестных. 2. Вращательное движ. тв. тела- движение в какой-либо системе отсчета, при котором существует проведенная в теле прямая, точки которой остаются неподвижными (ось вращения). Вводятся пересекающиеся по оси пл-ти: неподвижная, жестко связанная системой отсчета и подвижная, фиксированная в твердом теле. 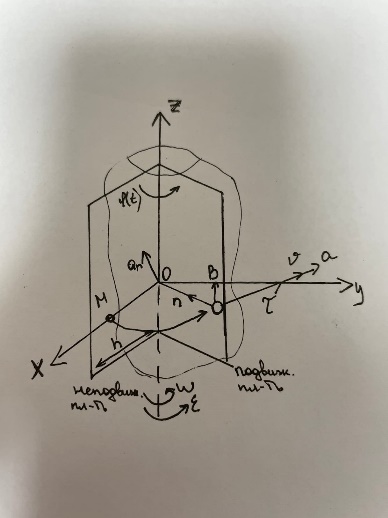 ϕ-угол поворота тела; ϕ(t)-закон вращения 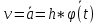 h - расстояние от точки до оси вращения h - расстояние от точки до оси вращенияϕ= ϕ(t)= 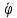 = =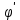 (t)= (t)=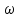 = =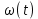 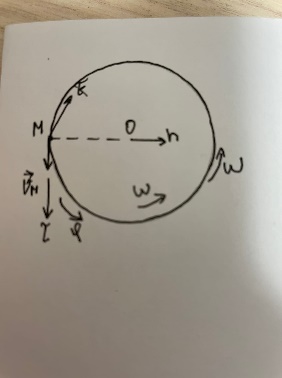 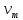 -линейная скорость; -линейная скорость; 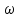 всегда направлен вдоль оси вращения всегда направлен вдоль оси вращения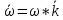 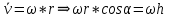 - связывает линейную скорость с угловой - связывает линейную скорость с угловой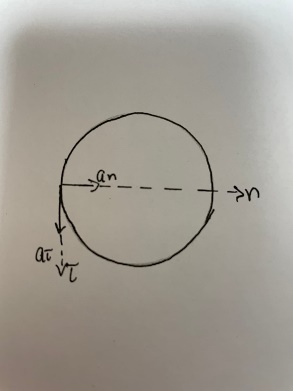 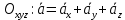 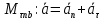 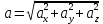 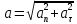 Касательное ускорение 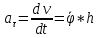 Нормальное ускорение 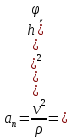 Угловое ускорение 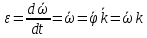 Векторное касательное ускорение 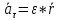 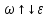 –равнозамедленное движ. –равнозамедленное движ.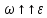 -равноускоренное движ. -равноускоренное движ.3. Кинетическая энергия механической системы равна сумме кинетической энергии поступательной части движения и кинетической энергии системы в ее относительном движении относительно центра масс. Если рассмотреть какую-нибудь точку системы с массой 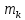 ,имеющую скорость ,имеющую скорость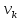 , то для этой точке будет , то для этой точке будет 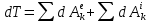 . Равенство выражает теорему об изменении кинетич. энергии в дифф-ой форме. Проинтегрировав обе части этого равенства в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна . Равенство выражает теорему об изменении кинетич. энергии в дифф-ой форме. Проинтегрировав обе части этого равенства в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна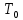 , в положение, где значение кинетической энергии становится равным , в положение, где значение кинетической энергии становится равным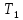 , получим , получим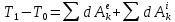 . Теорема: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил. . Теорема: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил. | Билет 19 1. Статически определимыми называют такие задачи, которые можно решить методами статики твердого тела, т.е. задачи, в которых число неизвестных не превышает числа уравнений равновесия. Статически неопределимыми называют задачи, с числом неизвестных, превышающих число уравнений равновесия, т.е. задачи, которые нельзя решать методами статики твердого тела и для решения, которых нужно учитывать деформации тела, обусловленного внешними нагрузками. 2. Поступательное движение твердого тела – движение в какой-либо системе отсчета, при котором любая прямая, состоящая из точек тела, остается параллельной самой себе. (например, педали велосипеда, колесо обозрения) Теорема: При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы. 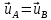 всегда, поэтому всегда, поэтому 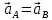 . . Следовательно, кинематика поступательного движения сводится к кинематике точки. 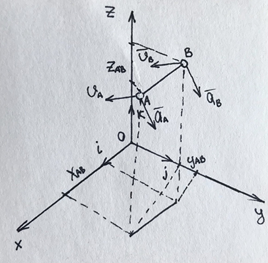 3. Кинетическая энергия механической системы – это сумма механических энергий всех ее материальных точек: 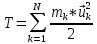 Если система состоит из нескольких твердых тел, то кинетическая энергия будет равна сумме кинетических энергий отдельных тел. Кинетическая энергия твердого тела при поступательном движении определяется так же, как для материальной точки: 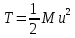 При вращательном движении: 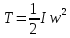 Билет 20 1. Точка C, через которую проходит линия действия равнодействующей системы парал. сил при любом одинаковом повороте этих сил вокруг точек их приложения, называется центром парал. сил; Если силы 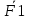 и и 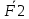 повернуть вокруг точек их приложения в одну и ту же сторону на одинаковый угол, то получится 2 новые парал. силы повернуть вокруг точек их приложения в одну и ту же сторону на одинаковый угол, то получится 2 новые парал. силы 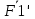 и и 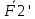 , равнодействующая которых , равнодействующая которых 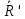 тоже пройдет через точку C; тоже пройдет через точку C;Центр парал. сил не меняет своего положения относительно точек приложения данных сил, если все силы, не нарушая их парал-ти, повернуть на один и тот же угол. 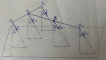 Пространственная система n парал. сил и равнодействующая этой системы: Пространственная система n парал. сил и равнодействующая этой системы: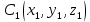 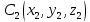 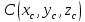 Формулы для определения координат центра парал. сил: 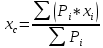 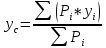 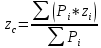 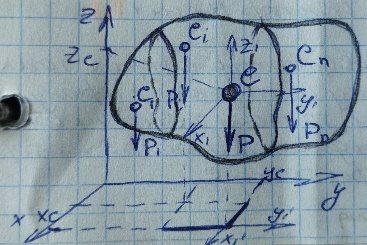 2. По определению: 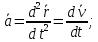 Ускорение точки находится в соприкасающ. к траектории плоскости. Соприкасающ. плоскость проводится через 3 точки траектории, стремящихся слиться в одну, совпадающ. по положению с матер-ой точкой. r ꓕ n ꓕ b Ускорение точки находится в соприкасающ. к траектории плоскости. Соприкасающ. плоскость проводится через 3 точки траектории, стремящихся слиться в одну, совпадающ. по положению с матер-ой точкой. r ꓕ n ꓕ b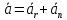 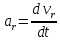 - касательное ускорение (проекция ускорения на орт r) - касательное ускорение (проекция ускорения на орт r) 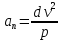 - нормальное ускорение (проекция на орт n) p- радиус кривизны траек-и в т. М - нормальное ускорение (проекция на орт n) p- радиус кривизны траек-и в т. М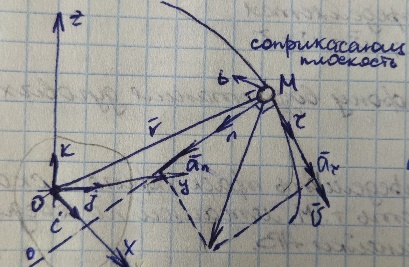 1.Если во время движения нормальное ускорение an=0, то движение точки является прямолинейным. an = 0, то 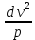 =0 и ρ=∞, т. е. траекторией являемся прямая. В этом случае: a = aτ. =0 и ρ=∞, т. е. траекторией являемся прямая. В этом случае: a = aτ. 2.Если в криволинейном движении точки в какой-нибудь момент времени an= 0, эта точка в данный момент находится в точке перегиба траектории. 3.Равномерное криволинейное движение. Если во время движения точки aτ=0, то 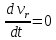 ; υτ=const. В этом случае точка движется равномерно по кривой и a=an. ; υτ=const. В этом случае точка движется равномерно по кривой и a=an.4.Если во время движения точки a = 0, то движение является равномерным и прямолинейным, так как скорость в этом случае не изменяется ни по величине, ни по направлению. 5.Если во время движения некоторой кривой aτ=const, то движение точки называется равнопеременным криволинейным движением. При этом если aτ совпадает с направлением скорости, то движение равноускоренное, а если не совпадает - равнозамедленное. Выразим скорость и закон движения точки s=s (t) в случае равнопеременного движения: Так как aτ= const, то υτ =const, υτ = aτt + С1; при t = 0, υτ = υ0 → С1 = υо; Так как υτ = s, то s= υ0+ aτt, ds= υ0dt+ aτtdt → s= υ0t+ 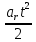 + С2 + С2при t = 0, s = s0 → С2 = s0; Получаем: s= s0+ υ0t+ 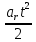 |
