|
|
Термех. Билет 1 1
Билет 25
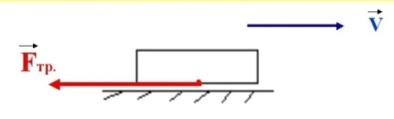
1. Сила трения –это сила,которая возникает при взаимодействии тел и препятствует их движению. 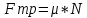
Трение скольжения –трение,возникающее при поступательном перемещении одного тела по поверхности другого.
Законы трения скольжения:
1)Если одно тело стремится сдвинуться относительно другого,то в плоскости их соприкосновения возникает сила трения скольжения в покое,F,величина которой может изменяться от нуля до
некоторого предельного значения,0<=F<=Fпр.
2)Величина Fпр. равна произведению статическогокоэффициента трения,fо,на величину нормального давления,N. 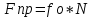
3)Величина предельной силы трения не зависит от размеров соприкасающихся при трении поверхностей.
2. Траектория – воображаемая линия,вдоль которой движется тело.Траектория может быть прямой и кривой,плоской и пространственной линией;
Скорость:
-средняя(отношение вектора перемещения ко времени,за которое это перемщение произошло) 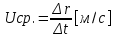
-мгновенная(скорость тела в данной точке в данный момент времени)
U=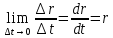 ; U= ; U=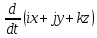
U=iUx+jUy+kUz;
Ускорение (характеризует быстроту изменения скорости движения):
a=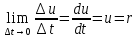 [м/с^2] [м/с^2]
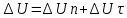
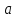 = =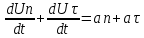 | |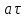 |=U^2/R |=U^2/R
3. Элементарная работа силы,приложенной к твердому телу,вращающемуся вокруг неподвижной оси,равна моменту этой силы относительно оси вращения,умноженному на дифференциал угла поворота тела
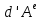 = =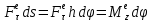
Билет 26
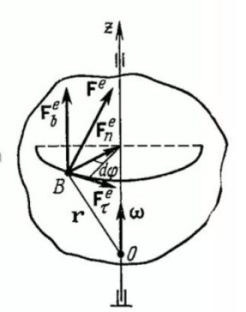
1. Реакция реальной (шероховатой) связи слагается из двух составляющих: из нормальной реакции N и перпендикулярной ей силы трения 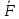 . Следовательно, полная реакция . Следовательно, полная реакция 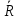 будет отклонена от будет отклонена от
нормали к поверхности на некоторый угол. При изменении силы
трения от нуля до 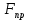 сила сила 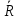 изменяется от изменяется от 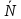 до до 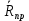 , а ее угол с нормалью растет от нуля до некоторого предельного значения , а ее угол с нормалью растет от нуля до некоторого предельного значения 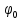 . Наибольший угол . Наибольший угол 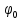 , который полная реакция шерохова той связи образует с нормалью к поверхности, называется углом трения. Из чертежа видно, что , который полная реакция шерохова той связи образует с нормалью к поверхности, называется углом трения. Из чертежа видно, что
tg 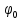 = =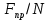
Так как 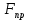 = = 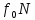 ,то отсюда находим следующую связь между ,то отсюда находим следующую связь между
углом трения и коэффициентом трения:
tg 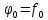
При равновесии полная реакция R в зависимости от сдвигающих сил может проходить где угодно внутри угла трения. Когда равновесие становится предельным, реакция будет отклонена от нормали на угол 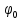
Если к телу, лежащему на шероховатой поверхности, приложить силу 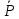 , образующую угол а с нормалью, то тело сдвинется только тогда, когда сдвигающее усилие , образующую угол а с нормалью, то тело сдвинется только тогда, когда сдвигающее усилие 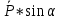 будет больше будет больше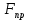 = = 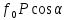 (мы считаем N = Pcosа, пренебрегая весом тела). Но неравенство (мы считаем N = Pcosа, пренебрегая весом тела). Но неравенство 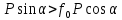 , в котором , в котором  , выполняется только при , выполняется только при 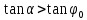 , т. е. при , т. е. при 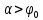 Следовательно, никакой силой, образующей с нормалью угол Следовательно, никакой силой, образующей с нормалью угол 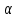 , меньший угла трения , меньший угла трения 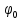 тело вдоль данной поверхности сдвинуть нельзя. Этим объясняются известные явления заклинивания или самоторможения тел. тело вдоль данной поверхности сдвинуть нельзя. Этим объясняются известные явления заклинивания или самоторможения тел.
Конусом трения называют конус, описанный полной реакцией, построенной на максимальной силе трения, вокруг направления нормальной реакции. Его можно получить изменяя активные силы так, чтобы тело на шероховатой поверхности находилось в предельных положениях равновесия, стремясь выйти из равновесия по всем возможным направлениям, лежащим в общей касательной плоскости соприкасающихся поверхностей.
Если коэффициент трения во всех направлениях одинаков, то конус трения круговой. Если не одинаков, то конус трения не круговой, например в случае, когда свойства соприкасающихся поверхностей различны (вследствие определенного направления волокон или в зависимости от направления обработки поверхности тел, если обработка происходит на строгальном станке и т. п.).
Изучение равновесия тел с учетом трения скольжения можно свести к рассмотрению предельного равновесия, которое имеет место, когда сила трения равна 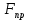 . .
При аналитическом решении реакцию шероховатой связи изобрfжают двумя ее составляющими N и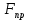 . Затем составляют обычные 66 . Затем составляют обычные 66
уравнения равновесия и присоединяют к ним равенство 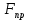 = =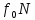 . Из полученной таким путем системы уравнений и определяют искомые величины. . Из полученной таким путем системы уравнений и определяют искомые величины.
Если в задаче требуется определить условия равновесия при всех значениях, которые может иметь сила трения, т. е. при F<=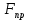 , то ее тоже можно решить, рассмотрев предельное равновесие и уменьшая затем в полученном результате коэффициент трения , то ее тоже можно решить, рассмотрев предельное равновесие и уменьшая затем в полученном результате коэффициент трения 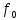 до нуля. до нуля.
2. Движение точки – изменение с течением времени её координат.
Способы задания движение точки:
1. 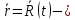 Закон движения точки при векторном способе задания её движения Закон движения точки при векторном способе задания её движения
2.x=X(t), y=Y(t), z=Z(t) – Закон движения точки при координатном способе задания движения
3. Естественный способ задания движения точки. Траектория – геометрическое место точек пространства, в которых во время движения прибывает материальная точка.
Дуговая координата – это отсчитываемые в соответствии с правилом знаков расстояние по траектории между точкой, принятой за начальную, и материальной точкой.
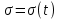 -закон движения точки по траектории -закон движения точки по траектории
Эквивалентное трёхмерное пространство – вычисления.
Движение представимо только в какой-то системе отсчета – в совокупности твёрдого тела, системы координат и часов.
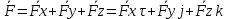
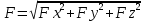
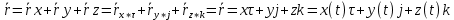
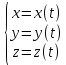
S=S(t)
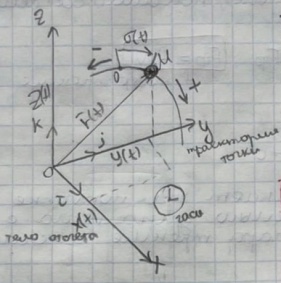
3.Принцип возможных (или виртуальных) перемещений. При равновесии механической системы с наложенными на нее идеальными связями сумма элементарных работ всех активных сил на любом возможном перемещении равна нулю:
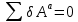
Это уравнение в механике называется общим уравнением статики или уравнением работ.
С учетом разных способов определения элементарной работы силы (табл. 3.3) уравнение работ можно записать и использовать в разных формах: векторная ,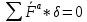 координатнат, координатнат, 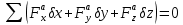
естественная 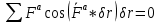
Принцип возможных перемещений – это динамический метод решения задач статики. Его преимущество перед методами геометрической статики состоит в том, что уравнение работ не включает в себя реакции идеальных связей. В случае, когда рассматривается равновесие системы тел, из рассмотрения исключаются заранее неизвестные реакции внутренних связей.
Например, чтобы найти соотношение между приложенным к кривошипу вращающим моментом М и уравновешивающей механизм силой F, приложенной к ползуну, геометрическая статика потребовала бы составить и решить совместно восемь уравнений равновесия. С помощью общего уравнения статики можно записать одно уравнение работ 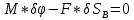 . С учетом геометрических соотношений между возможными перемещениями . С учетом геометрических соотношений между возможными перемещениями 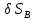 и и 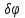 сразу получается результат: сразу получается результат:
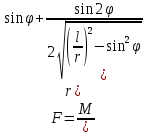
1. Принцип возможных перемещений можно использовать и при наличии неидеальных связей. Для этого в уравнение работ, наряду с работой активных сил, нужно включить работу реакций неидеальных связей.
2. Несмотря на то, что реакции связей не входят в уравнение работ, реакции связей можно найти с помощью принципа возможных перемещений. Для этого надо воспользоваться принципом освобождаемости от связей и в уравнение работ включить работу искомых реакций.
Билет 27
1. Т 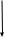
N
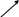
r
рение качения возникает при попытке «перекатить» друг относительно друга тела с криволинейной поверхностью, появляется пара трения качения с моментом m. Колесо покатится если только: F*r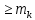 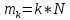
М
F
инимальная сила: F = 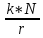
k-коэфф.трен.кач-ия
N

r
F

Fтр

Э
Fтр
 та зависимость подтверждается экспериментально. Для малой скорости качения сила трения качения не зависит от величины этой скорости. Когда скорость качения достигает значений, сопоставимых со значениями скорости деформации в материале опоры, трение качения резко возрастает и даже может превысить трение скольжения при аналогичных условиях. та зависимость подтверждается экспериментально. Для малой скорости качения сила трения качения не зависит от величины этой скорости. Когда скорость качения достигает значений, сопоставимых со значениями скорости деформации в материале опоры, трение качения резко возрастает и даже может превысить трение скольжения при аналогичных условиях.
Момент сил трения качения: Определим для подвижного цилиндра момент, торморзящий вращательное движ-ие тела. Рассматривая данный момент относ-но оси вращающегося колеса, находим, что он равен произведению тормозного усилия на оси на радиус колеса. Относ-но точки контакта движущегося тела с землей момент будет равен произведению внеш.силы, уравновешивающей силу трения, на радиус колеса: M=Fтр*r=F*r
С другой стороны, момент трения равен моменту прижимающей силы N на плечо, длина которого равна коэф-ту трения качения: M=k*N
2. Главная задача кинематики: математическое определение положения и характеристик движ-ия точек или тел во времени. (как движ-ся точка). Любое тело рассматривается в определенной системе отсчета.
Система отсчета- совокупность неподвижных относ-но друг друга тел, по отнош-ию к котрым рассматривается движ-ие, и отсчитывающих время часов, по отнош-ию к котрым рассматривается движ-ие каких-либо тел.
Механическое движ-ие- изменение положения тела (или его часте) в простран-ве относ-но др.тел с течением времени.
Движ-ие точки- изменение с течением времени ее координат. Способы задания движ-ия точки:
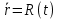 – закон движ-ия точки при векторном способе задания ее движ-ия – закон движ-ия точки при векторном способе задания ее движ-ия
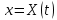 ; y=Y(t); z=Z(t) – закон движ-ия точки при координатном способе задания движ-ия ; y=Y(t); z=Z(t) – закон движ-ия точки при координатном способе задания движ-ия
Естественный способ задания движ-ия точки: Траектория- геометр.место точек простр-ва, в которых во время движ-ия пребывает мат.точка
Дуговая координата- отсчитываемое в соответствии с правилом знаков расстояние по траектории м/у точкой, принятой за начальную, и мат.точкой
S=S(t) –закон движ-ия точки по траектории
Движ-ие представимо только в какой-то системе отсчета- совокупности тв.тела, системы координат и часов.
 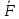 = =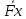 + +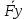 + +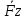 = = 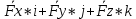
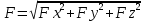 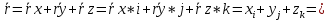 x(t)i+y(t)j+z(t)k связь векторного и координатного способа задания x(t)i+y(t)j+z(t)k связь векторного и координатного способа задания
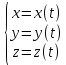 S=S(t) S=S(t)
Основными понятиями ньютоновской (классической) механики яв-ся абсолют.пространство, абсолют.время и мат.точка. Абослют.простран-во- неосязаемая бесконечная кристаллическая решетка, сквозь которую беспрепятственно могут перемещаться различные тела. Оно вмещает в себя всю материю, но от нее не зависит. Абсолют.время протекает равномерно, не зависит от свойств материи и от места в пространстве.
3. Принцип возможных перемещений – принцип, устанавливающий общее условие равновесия механической системы. При освобождении от связей добавляются неизвестные реакции связей, и одновременно рассматриваются бесконечно малые перемещения, которые допускаются сохраненными связями.
Порядок решения задач с помощью принципа возможных перемещений
1)Изобразить на рисунке активные силы
2)Если есть неидеальные связи, добавить соответствующие реакции связей (например, сила трения)
3)Предоставить возможное перемещение одной из точек системы, для чего, если система неподвижна, придать ей одну степень вольности
4)Выразить возможные перемещения точек приложения сил в зависимости от заданного возможного перемещения
5)Вычислить сумму работ всех сил на соответствующих возможных перемещениях их точек приложения и приравнять эту сумму к нулю
6)Решив составленное уравнение равновесия, определить искомую величину.
1) Изобразить на рисунке активные силы, действующие на механическую систему
2)Определить кол-во степеней свободы механической системы и выбрать независимые виртуальные перемещения точек системы в числе равном числу степеней свободы этой системы
3)Дать виртуальное перемещение, соответствующее одной из степеней свободы, считая при этом виртуальные перемещения, соответствующие остальным степеням свободы, равным нулю.
4) Вычислить сумму работ всех сил на соответствующих возможных перемещениях их точек приложения и приравнять эту сумму к нулю
5)Произвести такие выкладки для каждого из независимых возможных перемещений, составить систему уравнений равновесия в числе равном числу степеней свободы системы
6)Решив систему составленных уравнений равновесия, определить искомые велшичины
|
|
|
|
 Скачать 5.41 Mb.
Скачать 5.41 Mb.