Термех. Билет 1 1
 Скачать 5.41 Mb. Скачать 5.41 Mb.
|
|
3. Неизменяемая система материальных точек - система, расстояния между точками которой при движении системы не изменяются. Такой системой является всякое абсолютно твердое тело. 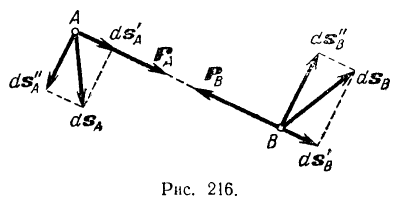 Допустим, что при движении системы за промежуток времени dt точки A и B получают элементарные перемещения d 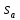 и d и d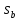 . Разложим каждое из этих перемещений на составляющие: одно, направленное по линии AB действия сил, и второе, перпендикулярное к этой линии. На перемещениях d . Разложим каждое из этих перемещений на составляющие: одно, направленное по линии AB действия сил, и второе, перпендикулярное к этой линии. На перемещениях d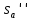 и d и d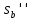 , перпенд-х к линиям действия сил, силы работы не производят. Так как расстояние между точками A и B неизменяемой системы при ее движении изменяться не может, то перемещения d , перпенд-х к линиям действия сил, силы работы не производят. Так как расстояние между точками A и B неизменяемой системы при ее движении изменяться не может, то перемещения d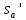 и d и d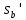 должны быть равны и направлены в одну сторону. Отсюда следует, что должны быть равны и направлены в одну сторону. Отсюда следует, что 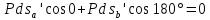 Таким образом, сумма работ внутренних сил неизменяемой системы при всяком ее перемещении равна нулю. Билет 21 1. Центр тяжести – точка твердого тела при закреплении которой само тело находится в равновесии в любом положении. Сумма моментов сил веса частей тела относительно его центра тяжести равна 0 в любом положении тела. 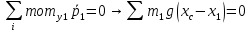 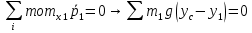 Координаты центра тяжести: 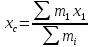 ; ;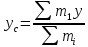 ; ; 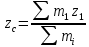 Т 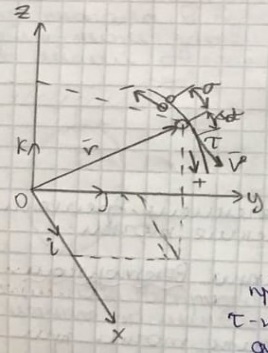 вердое тело состоит из набора частиц, которые обладают силой тяжести. Силы тяжести всех этих частиц направлены к центру Земли, но, учитывая, что размеры Земли несоизмеримо больше размеров тела, то эти силы можно считать параллельными. вердое тело состоит из набора частиц, которые обладают силой тяжести. Силы тяжести всех этих частиц направлены к центру Земли, но, учитывая, что размеры Земли несоизмеримо больше размеров тела, то эти силы можно считать параллельными.2 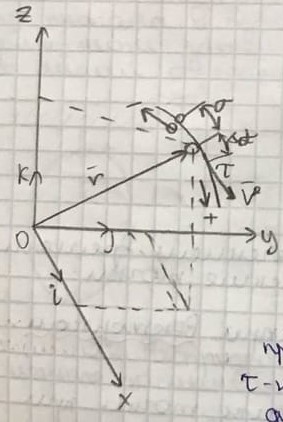 . Скорость точки при естественном способе задания движения точки. 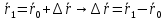 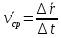 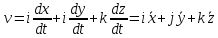 П 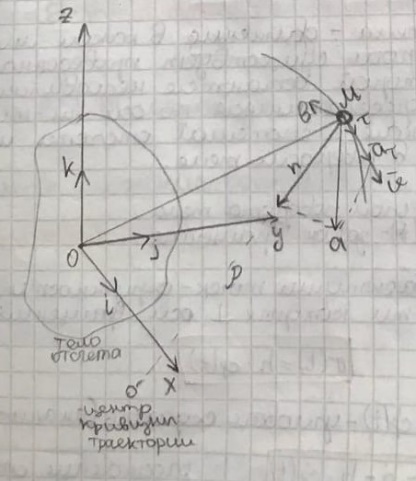 ри естественном способе задания движения точки проекция скорости на касательную к траектории ри естественном способе задания движения точки проекция скорости на касательную к траектории  определяeтся: определяeтся: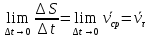 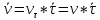 Ускорение точки при естественном способе задания движения точки.  По определению: 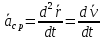 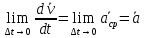 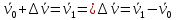 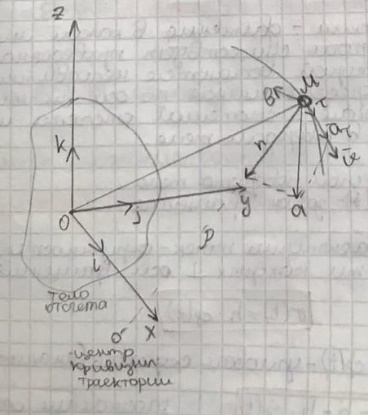 3. Теорема об изменении кинетической энергии механической системы формулируется: изменение кинетической энергии механической системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних cuл, приложенных к системе, на этом перемещении: 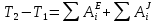 В случае неизменяемой системы сумма работ внутренних сил на любом перемещении равна нулю ( В случае неизменяемой системы сумма работ внутренних сил на любом перемещении равна нулю (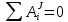 ), тогда ), тогда 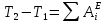 . .Билет 22 1. Центр тяжести тв. тела есть центр параллельных сил, представляющих веса материальных частиц тв. тела. Координаты центра тяжести однородного тела 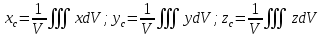 Координаты плоской фигуры( S-площадь) 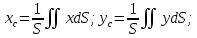 Координаты однородной линии длиною l 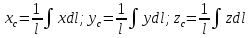 При вычислении координат ЦТ пользуются различными приемами позволяющими упростить вычисления. Теоремы упрощающие в некоторых случаях нахождение ЦТ Т1: Если однородное тело имеет ось симметрии по ЦТ тела находится на этой оси Применяя эту теорему к плоской фигуре или линии, легко установить, что если плоская фигура или линии имеет ось симметрии, то ее центр тяжести лежит на этой оси. Т2: если однородное тело имеет плоскость симметрии, то ее центр тяжести находится в этой плоскости. Выводы по двум теоремам: -ЦТ отрезка прямой лежит в его середине -ЦТ окружности, площади круга, поеверхности и объема шара находятся на их геом. центрах -ЦТ периметра и площади параллелограмма, ромба, прямоугольника и квадрата лежат в точках пересечения их диагоналей -ЦТ периметра и S правильного многоугольника находятся в центре вписанного( или описанного) круга Т3: Объем тела вращения полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описанной ее центром тяжести. Т4: Площадь пов-сти вращения, полученной вращением плоскости кривой вокруг оси, лежащей в плоскости этой кривой, но ее не пересекающей, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести 2. Естественными координатными осями называются три взаимно перпендикулярные оси: касательная, направленная в сторону возрастания дуговой координаты, главная нормаль, направленная в сторону вогнутости кривой, и бинормаль, направленная по отношению к касательной и главной нормали так же, как ось Оz направлена по отношению к осям Ох и Оу в правой системе координатных осей. Единичные векторы-орты этих осей обозначаются соответственно 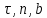 Естественные ур-я движения точки-получается проецированием диф-ого движения на естественные( подвижные) оси координат 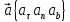 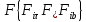 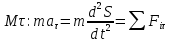 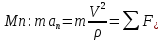 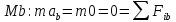 3. Возможными перемещениями несвободной механической системы называются воображаемые бесконечно малые перемещения, допускаемые в данный момент связями, наложенными на систему. Возможные перемещения точек системы изображают элементарным вектором , направление которого допускается связями. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ дает универсальные условия равновесия несвободных механических систем. При освобождении от связей добавляются неизвестные реакции связей, и одновременно рассматриваются бесконечно малые перемещения, которые допускаются сохраненными связями. Главное преимущество ПВП по сравнению с геометрической статикой: Рассматриваются механизмы, т.е. механические системы, в которых сохранено большинство внутренних связей. Интересующая реакция может быть найдена независимо от других! Возможными перемещениями несвободной механической системы называются воображаемые бесконечно малые перемещения, допускаемые в данный момент связями, наложенными на систему. СВОЙСТВА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ -ВП бесконечно малы и определены для мгновенного положения механизма; -при стационарных связях действительное перемещение совпадает с одним из возможных перемещений ; -при нестационарных связях действительное перемещение не совпадает ни с одним из возможных перемещений; -ВП не связаны с действием приложенных сил. ВП являются воображаемыми (возможными) и определяются только геометрией механической системы. Билет 23 1. Метод симметрии: если тело имеет плоскость симметрии, центр тяжести находится соответственно в плоскости симметрии, в центре симметрии. Метод разделения на части: если твердое тело можно разбить на такие части, положение центра тяжести которых известны, то центр тяжести тела находится как центр тяжести совокупности материальных точек. Метод отрицательных масс: заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей - отрицательной. Экспериментальный метод (способ Гульдена): 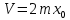 Из экспериментальных способов отметим метод взвешивания и подвешивания. Метод взвешивания: по известным весу тела P, показаниям весов R и расстоянию «а» определяют расстояние «х» из уравнения: 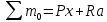 , отсюда , отсюда 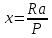 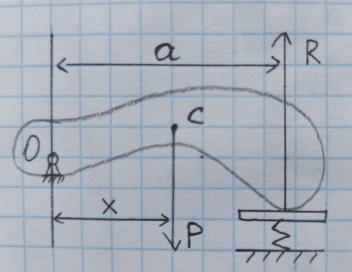 Метод подвешивания (применяются преимущественно для плоских тел). При этом способе тело подвешивают на нити сначала в одной точке и проводят линию, продолжают нить затем в другой точке. Точка пересечения этих линий определяет положение центра тяжести.  2.  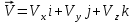 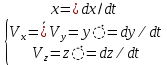 - определение скорости при координатном способе задания движения - определение скорости при координатном способе задания движения 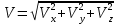 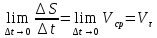 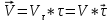 По определению: 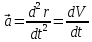 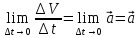 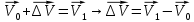 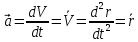 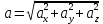 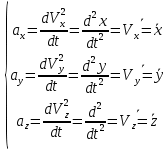 3. Связями механической системы называются любые ограничения, накладываемые на координаты и скорости точек этой системы. Идеальными называются связи, для которых элементарная работа и их реакций на любом возможном перемещении системы равна нулю, т. е 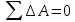 Например: тело на гладкой поверхности, реакция опоры направлена по нормали к поверхности,  S — возможное перемещение. S — возможное перемещение.Билет 24 1. В действительности взаимодействие одного тела с другим осуществляется либо по некоторой площадке, либо по объёму тела. Внешние силы: 1.) Поверхностные (делятся на: 1. Сосредоточенные 2. Распределенные) 2.) Объемные ( 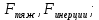 силы тяжести — они распределены по всему объёму тела, но часто, для удобства, мы заменяем эти силы их равнодействующей, приложенной к центру тяжести) силы тяжести — они распределены по всему объёму тела, но часто, для удобства, мы заменяем эти силы их равнодействующей, приложенной к центру тяжести)В механике рассматривают силы, приложенные к твердому телу в какой-либо его точке. Такие силы называют сосредоточенными. В инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности или линии по тому или иному закону. Распределенные силы характеризуются в каждой точке числовым значением и направлением вектора интенсивности q этой нагрузки, т.е. величиной силы, приходящейся на единицу поверхности, объема, площади или длины линии. Распределенные нагрузки возникают, если площадь контакта взаимодействующих тел соизмерима с площадью их поверхности. Р 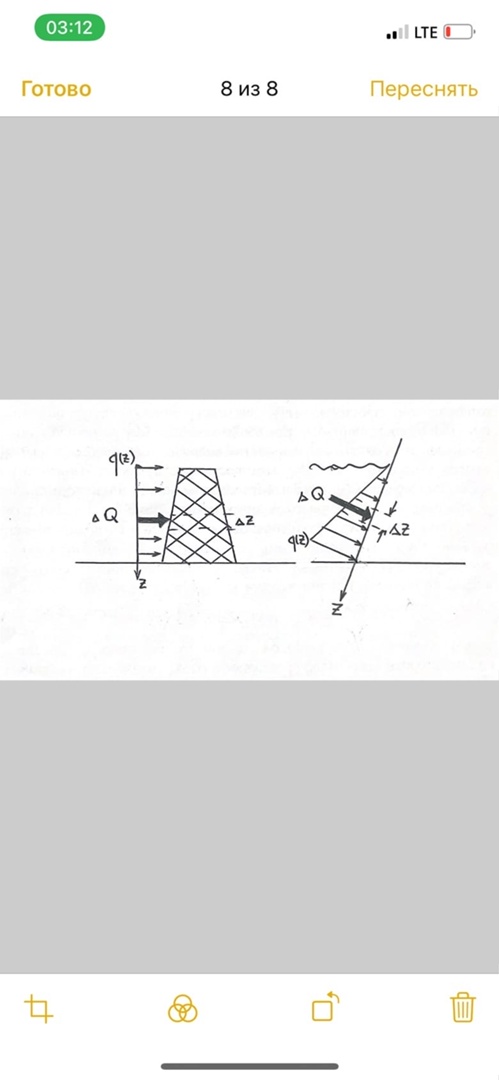 аспределенные нагрузки задаются интенсивностью. аспределенные нагрузки задаются интенсивностью. На плоскости: 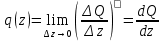 , где , где Q-нагрузка, приходящаяся на участок Q-нагрузка, приходящаяся на участок  c координатой z. c координатой z. (ветровая и водная нагрузки на рис.) Р 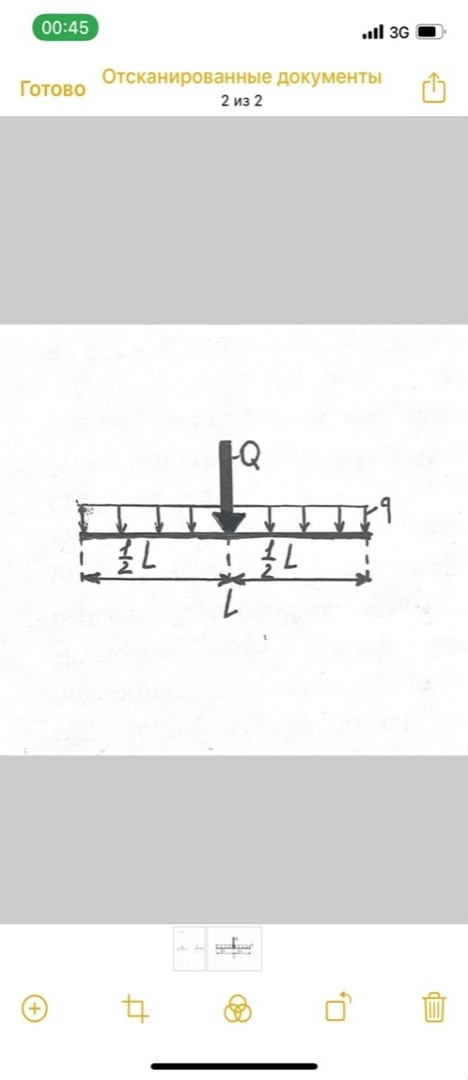 авномерно-распределенная нагрузка: авномерно-распределенная нагрузка: 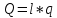 Линейно-распределенная нагрузка: 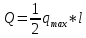  Примером линейно-распределенной Примером линейно-распределенной нагрузки может служить давление воды на плотину. 2 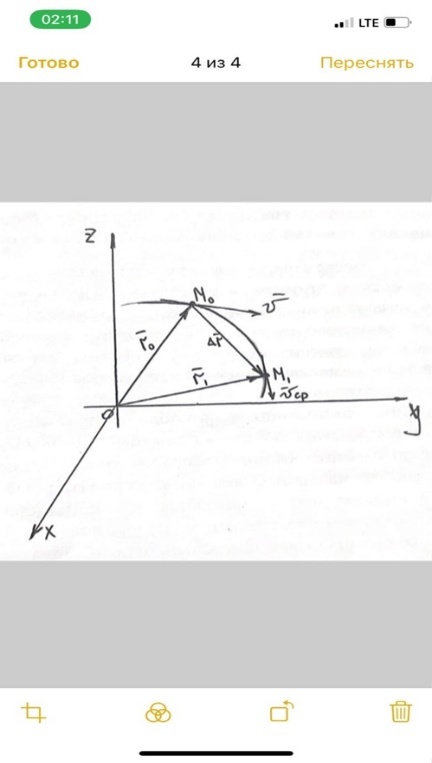 . .Скорость: При векторном способе задания движения положение движущейся точки в каждый момент времени определяется радиусом – вектором, который в свою очередь является функцией времени 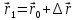 → → 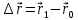 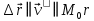 ; ;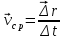 → →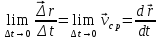 = =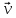 ( 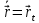 ) )Вектор скорости точки в данный момент времени равен первой производной по времени от радиуса-вектора данной точки. Ускорение:   Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости и второй производной от радиус-вектора точки по времени. Вектор ускорения a направлен по касательной к вектору скорости V в сторону вогнутости траектории 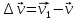 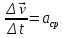 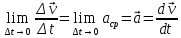 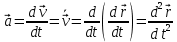 = =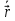 3. Принцип Даламбера – общий метод, при помощи которого уравнения динамики по форме предается вид уравнения статики. Благодаря простоте этот метод получил широкое практическое применение. 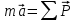 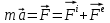 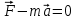 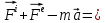 0 0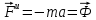 – даламберова сила – даламберова сила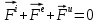 - для любого тела - для любого тела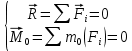 – для равновесного состояния – для равновесного состоянияС ведением силы инерции (даламберова сила) уравнение динамики тоже принимает вид уравнения равновесия: 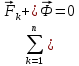 Геометрическая сумма приложенных к точке сил и силы инерции этой точки равны 0. Сила инерции условно добавляется к действиям на точку силам образуя взаимно уравновешенную систему сил. |
