!Конспект лекций Теоретичекая и прикладная механика. Лекция 1 Предмет теоретической механики. Кинематика точки
 Скачать 3.52 Mb.
|
ГЛОССАРИЙ
Домашнее задание - пользуясь теоремой о движении центра масс решить самостоятельно следующую задачу: сидящий в лодке охотник стреляет вперед в горизонтальном направлении. Пренебрегая сопротивлением воды, определить скорость лодки после выстрела, если до выстрела она была неподвижна; масса охотника 70 кг, масса лодки 30 кг, масса заряда 40 г и его начальная скорость 300 м/с. См. Курс теоретической механики (под ред. Колесникова К.С.), Москва, издательство МВТУ им.Н.Э.Баумана,2000-736с. Лекция 12. Теорема об изменении количества движения Цель лекции - изложить теорему об изменении количества движения для материальной точки и механической системыПлан лекцииКоличество движения материальной точки и механической системы. Элементарный и полный импульс силы Теорема об изменении количества движения КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Количеством движения точки материальной точки называется векторная величина, равная произведению массы точки на вектор ее скорости  Проекция вектора 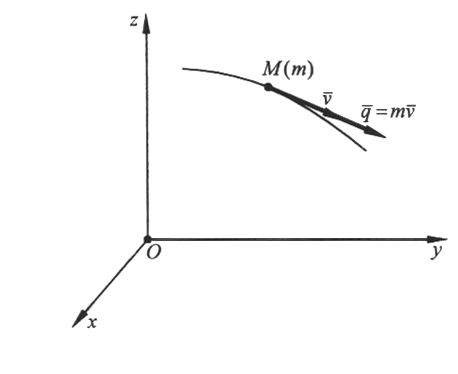 на координатные оси координат   . Рис.1Количеством движения механической системы называется вектор 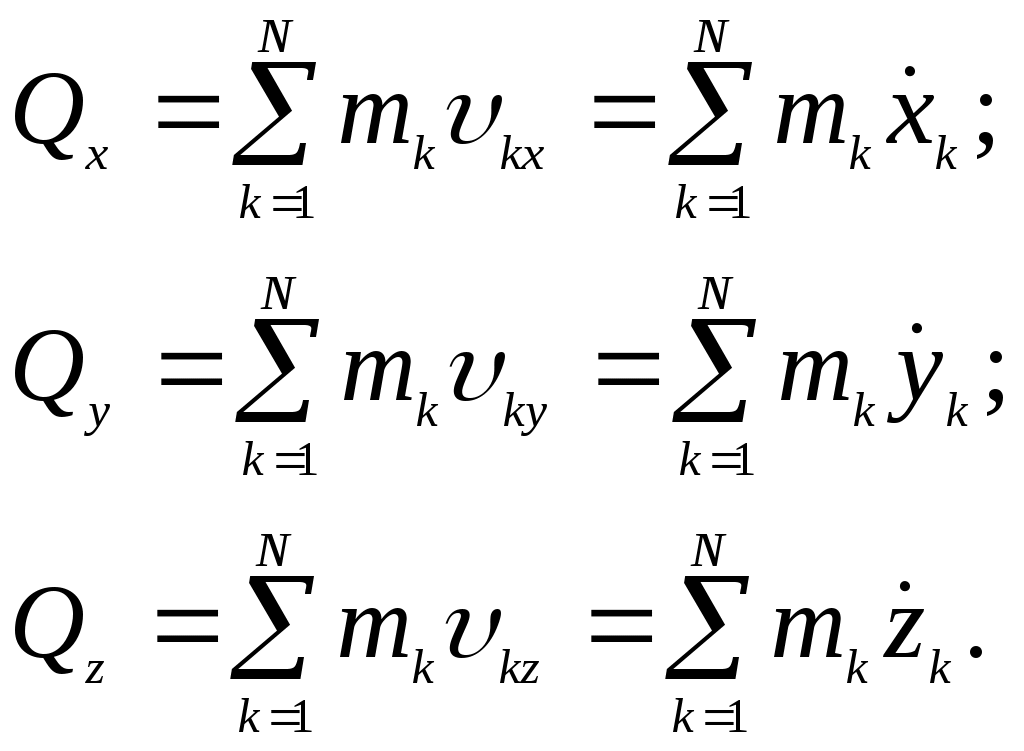 , равный геометрической сумме количеств движения всех точек системы: Вектор является свободным вектором. Проекции вектора на координатные оси будут иметь вид:  Единица измерения в системе СИ – кг ∙м/с . Используя понятие центра масс механической системы, количество движения системы будет  .Проекции этого вектора 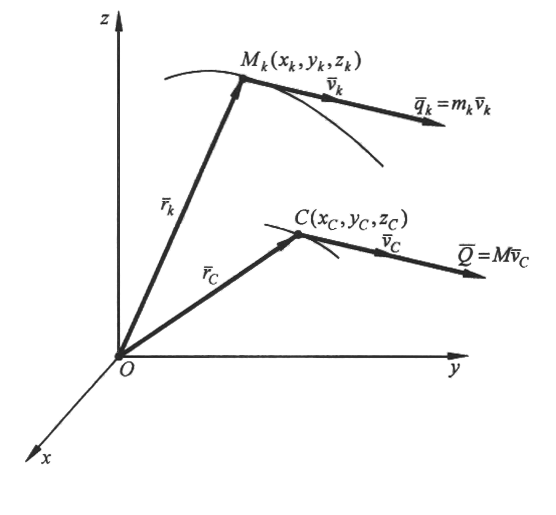  . Рис.2Элементарным импульсом силы  за элементарный промежуток времени  называется векторная величина, равная  . Проекции на координатные оси    .Полный импульс силы  за конечный промежуток времени  равен: .Проекции вектора полного импульса на координатные оси:    .Единица измерения импульса силы – Ньютон ∙ секунда (Н∙ с). Движение материальной точки описывается следующим уравнением: ,или  в проекциях на оси координат    Используя понятия импульса силы и количества движения, запишем  , В проекциях на оси координат:    Интегрируя в заданных пределах, будем иметь 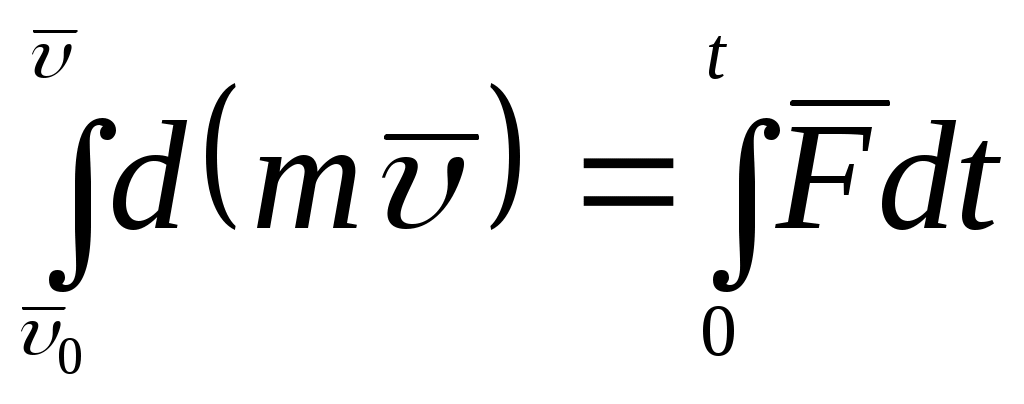 .Отсюда  , где  - конечная и начальная скорости; - полный импульс силы за время . Это уравнение выражает теорему об изменении количества движения точки: изменение количества движения точки за некоторый промежуток времени равно импульсу действующей на точку силы за тот же промежуток времени.В проекциях на оси координат: 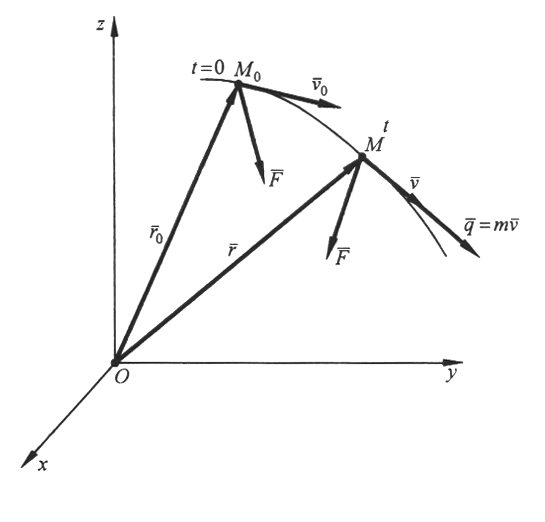    . Рис.3 Теорему о движении центра масс системы механической системы запишем в виде:  отсюда получим:  . Окончательно будем иметь:  . Это уравнение выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех внешних сил, действующих на систему. Проектируя обе части этого уравнения на координатные оси, получим:    Умножая обе части уравнения на dt:  . Поэтому, дифференциал количества движения механической системы равен геометрической сумме элементарных импульсов всех внешних сил, действующих на систему. Проекции на координатные оси будут   .Интегрируя уравнения в заданных пределах, получим: 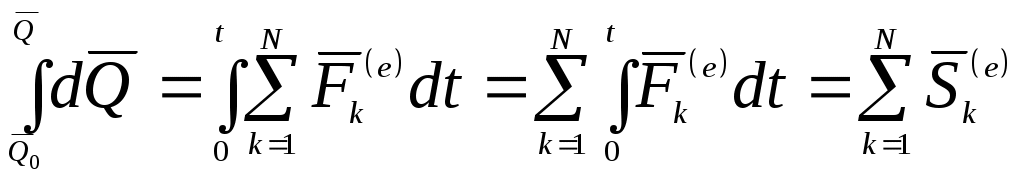 , или  , где   - количества движения системы в начальный и конечный моменты времени.Последнее уравнение выражает теорему в интегральной форме: изменение количества движения системы за какое-либо время равно сумме импульсов всех внешних сил, действующих на систему за то же время. В проекциях на оси координат уравнения будут иметь вид:    .Теорема допускает первый интеграл (закон сохранения) в случае: если геометрическая сумма всех внешних сил равна нулю:  . Тогда вектор количества движения системы будет постоянен по модулю и по направлению:  . ГЛОССАРИЙ
Домашнее задание – ответить на следующие вопросы: 1). Влияют ли внутренние силы системы на ее количество движения? На движение ее центра масс? 2). При каких условиях центр масс находится в покое? Лекция 13. Теорема об изменении момента количества движения |