!Конспект лекций Теоретичекая и прикладная механика. Лекция 1 Предмет теоретической механики. Кинематика точки
 Скачать 3.52 Mb.
|
|
Мощность. Отношение приращения работы силы к элементарному промежутку времени, за которое оно произошло, называется мощностью:  .Так как  , то  .Таким образом, мощность силы равна скалярному произведению силы на скорость точки ее приложения. Единица измерения мощности в системе СИ 1 Ватт  .Работа внутренних сил, приложенных к твердому телу. Рассмотрим две произвольные точки тела А и В (Рис.3), силы взаимодействия которых, согласно третьему закону Ньютона  , на основании формулы (6) имеем: .Раскрывая скалярные произведения двух векторов, получаем 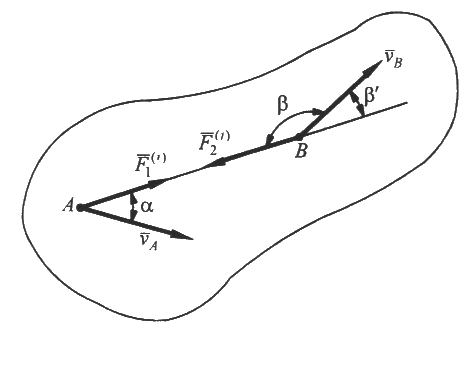  , так как  . Рис.3 Работа силы при поступательном движении твердого тела. При поступательном движении твердого тела векторы скоростей, а также элементарные перемещения всех точек тела одинаковы. Тогда элементарная работа силы  .Полная работа силы на каком-либо перемещении будет 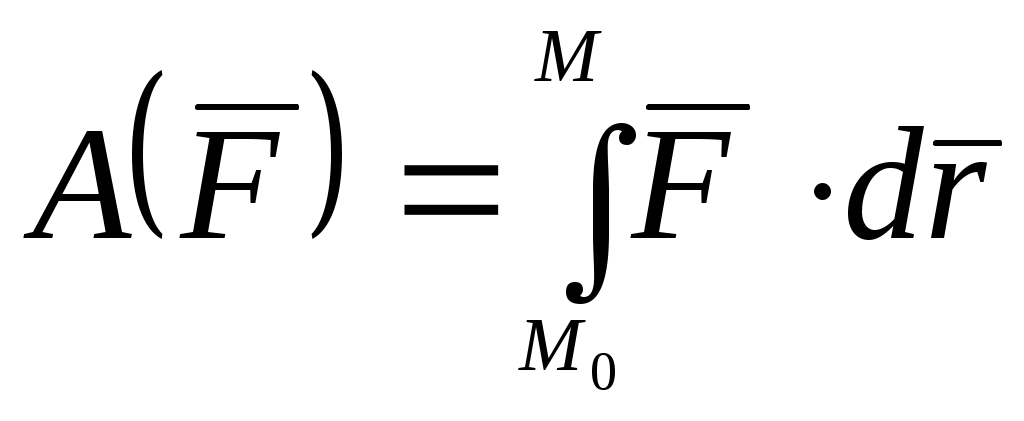 .Работа силы при вращении твердого тела вокруг неподвижной оси. Разложим силу  , приложенную в произвольной точке М тела, по осям  естественного трехгранника (Рис.4): .Работы составляющих силы по нормали и бинормали равны нулю, ибо они направлены всегда перпендикулярно к вектору скорости точки М. Поэтому 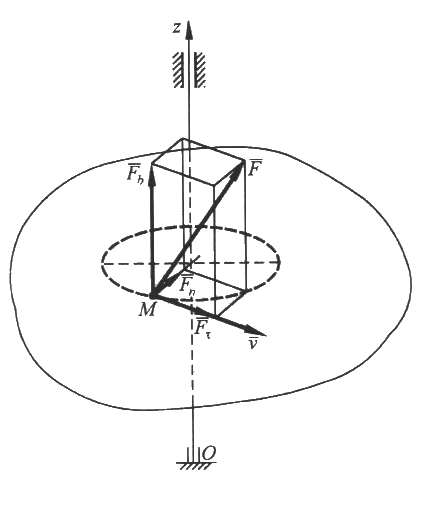 . Рис.4 Поскольку  , то где  кратчайшее расстояние от точки приложения силы до оси вращения.Учитывая, что  - момент силы относительно оси  , получаем: Таким образом, элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента этой силы относительно оси вращения на дифференциал угла поворота тела. Полная работа  .В случае, когда момент силы относительно оси вращения тела постоянен, полная работа  .Мощность силы в рассматриваемом случае  , где  - проекция на ось угловой скорости.Работа силы в общем случае движения свободного тела. Скорость точки М приложения силы  (Рис.5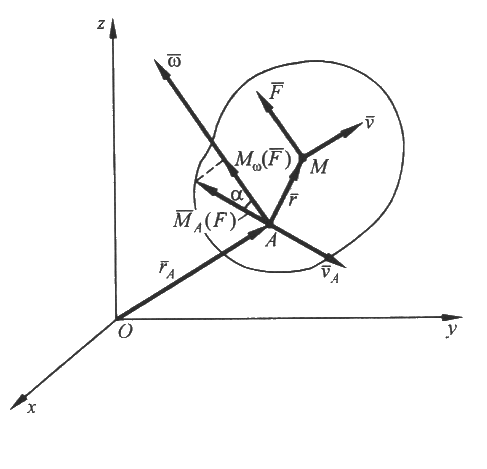) в рассматриваемом случае равна , где  - скорость полюса А ;  . Тогда .Рис.5  Так как  то , или , где  проекция  на вектор  ;  - элементарный угол поворота тела вокруг мгновенной оси относительно вращенияТаким образом, элементарная работа силы, приложенной к какой-либо точке твердого тела, в общем случае его движения равна сумме элементарных работ на элементарном поступательном перемещении вместе с полюсом и элементарном вращательном перемещении вокруг мгновенной оси, проходящей через полюс. ГЛОССАРИЙ
Домашнее задание – рассмотреть самостоятельно работы силы упругости, силы трения, силы трения качения См. Никитин Н.Н. Курс теоретической механики, Москва, Высшая школа, 1990 – 607с. Лекция 15. Кинетическая энергия. Теорема об изменении кинетической энергии точки и механической системы Цель лекции – изложить теорему об изменении кинетической энергии План лекции Кинетическая энергия материальной точки и механической системы. Вычисление кинетической энергии при различных движениях твердого тела Теоремы об изменении кинетической энергии материальной точки и механической системы. Закон сохранения механической энергии КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ Кинетическая энергия материальной точки и системы. Кинетическую энергию материальной точки определяют по формуле:  , где  есть скорость точки . Кинетическая энергия механической системы равна сумме кинетических энергий всех точек системы:  Кинетическая энергия – положительная скалярная величина. Единицей измерения кинетической энергии в системе СИ является – джоуль (1Дж=1Н∙м) . Кинетическая энергия твердого тела. При поступательном движении твердого тела скорости всех точек одинаковы и равны скорости центра масс, поэтому кинетическая энергия  , где - масса твердого тела.При вращении твердого тела вокруг неподвижной оси скорость его произвольной точки  .Тогда  ,где  - момент инерции тела относительно оси вращения.При плоском движении твердого тела, которое можно рассматривать как совокупность поступательного движения вместе с центром масс С и вращения вокруг подвижной оси CZ с угловой скоростью  , кинетическая энергия тела будет определяться формулой: , где  момент инерции тела относительно оси OZ.Теорема об изменении кинетичской энергии материальной точски. Движение точки массы m под действием силы определяется уравнением , которое можно также записать в виде . Умножив обе части уравнения скалярно на  , после преобразований  , получим . Эта формула выражает теорему об изменении кинетической энергии точки в дифференциальной форме: дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку. Разделив обе части уравнения на  , получим еще одну запись теоремы в дифференциальной форме: .После интегрирования получим  где  - кинетическая энергия точки в начальный и конечный моменты времени соответственно.Эта формула выражает теорему об изменении кинетической энергии в интегральной форме: изменение кинетической энергии точки на любом перемещении равно работе силы, действующей на точку, на том же перемещении. Теорема об изменении кинетической энергии механической системы. Для механической системы, на которую действуют как внешние, так и внутренние силы, можно записать:   Суммируя левые и правые части этих уравнений по всем точкам системы и вынося знак дифференциала за знак суммы, получаем:  , или Дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.Разделив обе части уравнения на . Тогда .Таким образом, первая производная по времени от кинетической энергии системы равна сумме мощностей всех внешних и внутренних сил, действующих на точки системы Проинтегрировав дифференциальные уравнения, будем иметь  , где 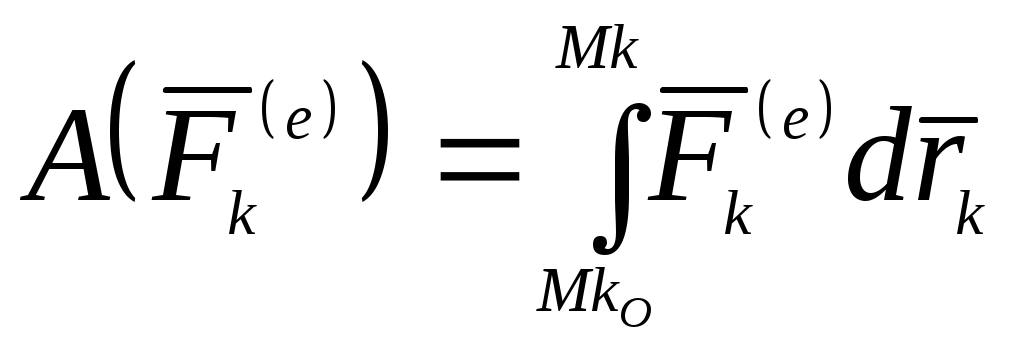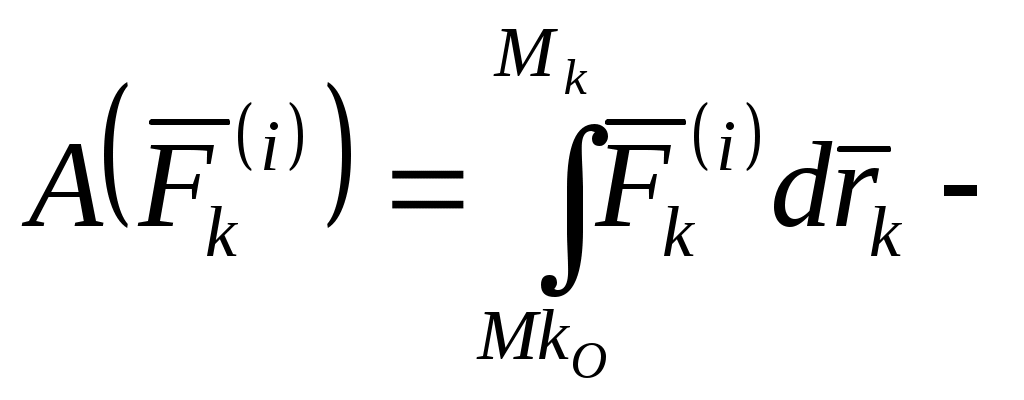- кинетическая энергия системы в начальном и текущем положениях соответственно;  , соответственно работа внешней и внутренней силы, действующей на k-ю точку системы. Таким образом : изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек приложения этих сил. Пусть все силы, действующие на систему потенциальны, т.е существует функция  , такая, что  , где  равнодействующая всех сил, приложенных к k-ой точке. Теорему об изменении кинетической энергии системы в дифференциальной форме представим в виде:  , где  .Тогда   ,окончательно  , или , где  - потенциальная энергия системыСледовательно,  , отсюда получаем Эта формула выражает закон сохранения механической энергии для механической системы: если все силы,действующие на систему, потенциальны, то при движении системы ее полная механическая энергия постоянна. ГЛОССАРИЙ
|