динамический анализ. Динамический анализ механизмов. Динамический анализ механизмов 1 Динамическая модель механизма
 Скачать 1.99 Mb. Скачать 1.99 Mb.
|
Динамический анализ механизмов4.1 Динамическая модель механизмаВ динамике механизмов изучается их движение с учетом действующих сил. 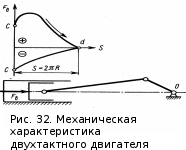 На рис.32 в качестве примера приведена зависимость движущей силы от перемещения поршня – механическая характеристика двухтактного двигателя. При расширении газов (движение поршня вправо) совершается положительная работа, а при сжатии (движение поршня влево) – отрицательная. Графически работа изображается площадью. В рассматриваемом случае положительная площадь больше отрицательной. В таком случае работа движущих сил будет больше работы сил сопротивления. На рис.32 в качестве примера приведена зависимость движущей силы от перемещения поршня – механическая характеристика двухтактного двигателя. При расширении газов (движение поршня вправо) совершается положительная работа, а при сжатии (движение поршня влево) – отрицательная. Графически работа изображается площадью. В рассматриваемом случае положительная площадь больше отрицательной. В таком случае работа движущих сил будет больше работы сил сопротивления.На рис.33 представлены механические характеристики электродвигателей постоянного тока последовательного возбуждения (рис.33,а) и асинхронного (рис.33,6), а на рис.33, в – характеристики вентилятора в зависимости от скорости. 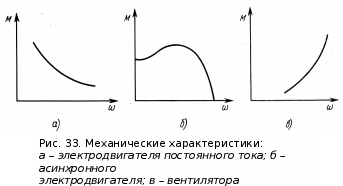 Эти характеристики получаются либо путем расчета, либо строятся по экспериментальным данным. Если все приложенные к звеньям силы известны, то можно определить закон движения какого-либо звена и механизма. Однако практическое решение этой задачи оказывается весьма сложным. Поэтому, как правило, прибегают к отдельным частным решениям, применяя способы приближенного определения движения механизма. Для этого сложный многозвенный механизм заменяют его динамической моделью. Если механизм имеет только одну степень подвижности, то в качестве модели механизма принимают одно условное звено. Так, для системы двигатель внутреннего сгорания (ДВС) – рабочая машина выбирают в качестве начального звена коленчатый вал ДВС. Закон движения условного звена должен полностью совпадать с законом движения начального звена. При этом угловые скорости начального и условного звеньев должны быть равны. При построении модели механизма все силы и моменты, действующие на его звенья, должны быть приведены к одному звену, называемому приведенным, и заменены приведенной силой или приведенным моментом. Таким же образом массы и моменты инерции всех звеньев приводят к тому же самому звену и заменяют суммарной приведенной массой или суммарным приведенным моментом инерции, которые эквивалентны всей инерции механизма. В итоге заданный многозвенный механизм, нагруженный сложной системой сил и моментов, заменяют простой моделью, состоящей из одного приведенного звена. 4.2 Приведение сил и моментов сил.Рассмотрим произвольный плоский механизм, состоящий из n звеньев, на каждое из которых действуют силы и моменты сил. При замене механизма его динамической моделью эти силы и моменты заменяются приведенной силой или приведенным моментом, приложенными к звену приведения. При этом должно соблюдаться следующее условие: мощность РП, развиваемая приведенной силой или приведенным моментом силы, должна быть равна сумме мощностей Рi всех сил и моментов, приложенных к звеньям механизма, или 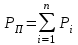 (4.1) (4.1)Мощность сил и моментов, приложенных к i-му звену (рис.34), равна 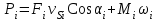 , (4.2) , (4.2)где Fi – модуль главного вектора внешних сил; vSi – модуль вектора скорости точки Siприложения вектора Fi; αi – угол между главным вектором сил Fi и вектором скорости vSi;  Мi – главный момент сил, действующих на звено относительно точки Si; Мi – главный момент сил, действующих на звено относительно точки Si;ωi – угловая скорость звена. Если звено приведения совершает вращательное движение с угловой скоростью ω (рис.35), то определяется приведенный момент МП. Мощность, развиваемая приведенным моментом, равна 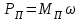 (4.3) (4.3)Подставляя выражения (4.2) и (4.3) в условие (4.1), определяем приведенный момент: 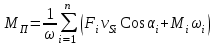 (4.4) (4.4)Если звено приведения совершает поступательное движение со скоростью v (рис.36), то определяется приведенная сила FП. Как правило, направление вектора приведенной силы FП выбирают совпадающим с направлением вектора скорости звена приведения v. При этом мощность, развиваемая приведенной силой, равна 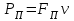 (4.5) (4.5)Подставляя выражения (4.2) и (4.5) в условие (4.1), определяем величину модуля приведенной силы: 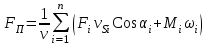 (4.6) (4.6) 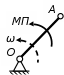  б) а) 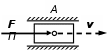  Рис.35. Приведение сил и моментов: а – для вращательного звена приведения; б – для поступательного звена приведения 4.3 Приведение масс и моментов инерцииКаждое i-е звено механизма обладает массой mi, которую принято считать сосредоточенной в центре масс звена, и моментом инерции JSi относительно оси, проходящей через центр масс. При замене механизма его динамической моделью массы и моменты инерции звеньев заменяются приведенной массой или приведенным моментом инерции звена приведения. Приведение масс и моментов инерции производится из условия равенства суммы кинетических энергий Кi звеньев рассматриваемого механизма и кинетической энергии КП приведенного механизма: 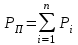 (4.7) (4.7) Кинетическая энергия i-го звена, совершающего плоскопараллельное движение, равна 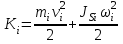 (4.8) (4.8)Если звено приведения совершает поступательное движение со скоростью v, то определяется приведенная масса mП. Кинетическая энергия звена приведения в этом случае равна 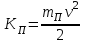 (4.9) (4.9)Подставляя выражения (4.8) и (4.9) в условие (4.1), определяем приведенную массу: 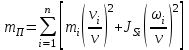 (4.10) (4.10)Полученная формула позволяет вычислить приведенную массу звена приведения, совершающего поступательное или вращательное движение. Переменная приведенная масса является условной величиной, которой пользуются для упрощения динамических расчетов. Поэтому звено приведения нельзя рассматривать в качестве твердого тела с действительно изменяющейся массой. Если звено приведения совершает вращательное движение с угловой скоростью ω (рис.35), то определяется приведенный момент инерции JП. Кинетическая энергия звена приведения в этом случае равна 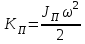 (4.11) (4.11) Подставляя выражения (4.8) и (4.11) в условие (4.1), определяем приведенный момент инерции: 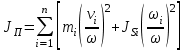 (4.12) (4.12)В формулах (4.10) и (4.12) отношения скоростей не зависят от действительных скоростей механизма, но зависят от положения механизма и положения его звеньев, включая и звено приведения. Следовательно, приведенная масса и приведенный момент инерции являются функциями только положения звена приведения. Если звено приведения совершает поступательное движение, то mП= f(s), a если вращательное, то JП = f(φ). Для большого класса механизмов mП и JП являются постоянными величинами (зубчатые механизмы с круглыми колесами, турбины, компрессоры и др.). Когда передаточное отношение в механизме не меняется (зубчатые и другие механизмы), приведенный момент инерции остается постоянным, а его значение — всегда положительно. Так как отношения скоростей отдельных точек механизма зависят только от его положения, то приведенный момент инерции не зависит от скорости движения механизма. 4.4 Уравнение движения механизмаКинетические параметры механизма при заданных массах звеньев и силах можно определить из уравнения Лагранжа II рода, изучая движение звена приведения. С учетом сил сопротивления движению приведенный момент сил будет 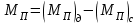 где (МП)д – приведенный момент движущих сил; (МП)с — приведенный момент сил сопротивления. При этом уравнение движения 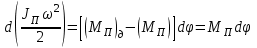 или 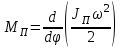 (4.13) (4.13)С учетом зависимости 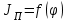 уравнение (4.13) дифференцируют как функцию двух независимых переменных JП и ω: уравнение (4.13) дифференцируют как функцию двух независимых переменных JП и ω: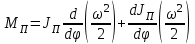 , ,где 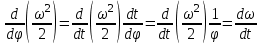 Отсюда дифференциальное уравнение движения для вращающегося звена приведения механизма принимает вид 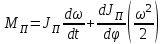 (4.14) (4.14)По аналогии дифференциальное уравнение поступательно движущегося звена приведения будет 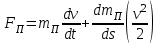 , (4.15) , (4.15) где FП – приведенная сила от движущих сил и сил сопротивления; s и v – перемещение и скорость звена приведения; mП – приведенная масса. В том случае, когда JП = const или mП = const, что имеет место в механизмах с постоянными передаточными отношениями, уравнения (4.14) и (4.15) принимают вид: 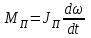 (4.16) (4.16)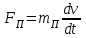 , (4.17) , (4.17) |
