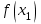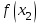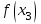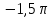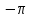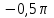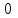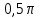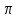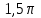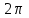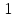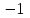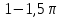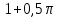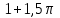уа. диплом2. Дипломды Жмыс таырыбы Функциялармен тедеулерді графиктерін трызуа координаттар дісін олдану
 Скачать 3.49 Mb. Скачать 3.49 Mb.
|
|
2.2 Функцияның графигін координаталық әдіспен тұрғызу Координаталық әдіс - бұл нүктенің немесе дененің орнын сандар немесе басқа белгілер арқылы анықтау тәсілі. Жазықтықта тікбұрышты координаталар жүйесін таңдап, абсцисса осіне 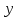 аргументінің мәндерін, ордината осіне аргументінің мәндерін, ордината осіне  функциясының мәндерін салайық. функциясының мәндерін салайық. функциясының графигі абсциссалары функцияның анықталу облысына жататын, ал ординаталары функцияның сәйкес мәндеріне тең болатын барлық нүктелердің жиыны болып табылады. функциясының графигі абсциссалары функцияның анықталу облысына жататын, ал ординаталары функцияның сәйкес мәндеріне тең болатын барлық нүктелердің жиыны болып табылады.Басқаша айтқанда,  функциясының графигі - жазықтықтағы барлық нүктелердің жиыны, ал функциясының графигі - жазықтықтағы барлық нүктелердің жиыны, ал 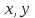 координаталары координаталары  қатынасын қанағаттандырады. қатынасын қанағаттандырады.11, 12-суретте 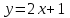 және және 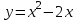 функцияларының графиктері көрсетілген. функцияларының графиктері көрсетілген.Графиктің көмегімен нүктедегі функцияның мәнін табуға болады. Атап айтқанда, егер 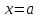 нүктесі нүктесі  функциясының анықталу облысына жататын болса, онда функциясының анықталу облысына жататын болса, онда 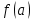 санын табу үшін (яғни, функцияның санын табу үшін (яғни, функцияның 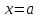 нүктесіндегі мәні), келесідей істеу керек. Абсциссасы нүктесіндегі мәні), келесідей істеу керек. Абсциссасы 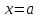 нүкте арқылы нүкте арқылы  осіне параллель түзу жүргізу керек; бұл түзу осіне параллель түзу жүргізу керек; бұл түзу  функциясының графигін бір нүктеде қиып өтеді; Бұл нүктенің ординатасы графиктің анықтамасы бойынша функциясының графигін бір нүктеде қиып өтеді; Бұл нүктенің ординатасы графиктің анықтамасы бойынша 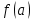 мәніне тең болады (13-сурет). мәніне тең болады (13-сурет).Мысалға, 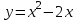 функциясының графигі (12-сурет) арқылы функциясының графигі (12-сурет) арқылы  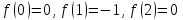 , т.с.с. екенін білеміз. , т.с.с. екенін білеміз.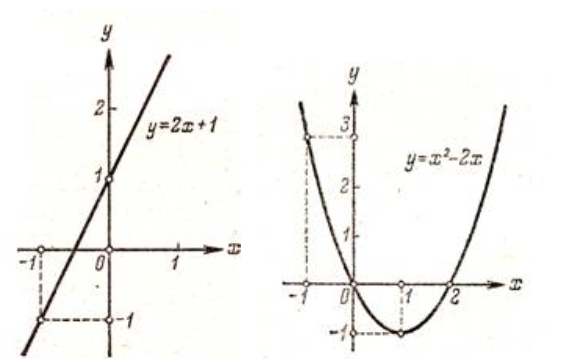 11-сурет 12-сурет Функция графигі функцияның әрекеті мен қасиеттерін көрнекі түрде көрсетеді. Мысалы, 12-суретті қарастырудан 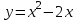 функциясы функциясы 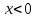 және және 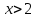 үшін оң мәндерді, ал үшін оң мәндерді, ал  үшін теріс мәндерді қабылдайтыны анық; үшін теріс мәндерді қабылдайтыны анық; 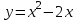 функциясы функциясы 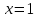 кезінде ең кіші мәнді қабылдайды. кезінде ең кіші мәнді қабылдайды.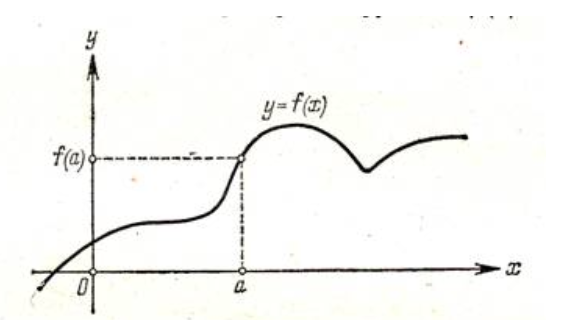 13-сурет 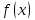 функциясының графигін салу үшін функциясының графигін салу үшін  теңдеуін қанағаттандыратын жазықтықтың барлық теңдеуін қанағаттандыратын жазықтықтың барлық 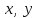 нүктелерінің координаталарын табу керек. Мұндай нүктелер шексіз көп болғандықтан бұл мүмкін емес деуге болады. Сондықтан функцияның графигі үлкен немесе аз дәлдікпен жуықтап бейнеленген. График тұрғызудың ең қарапайым әдісі координаталық нүктелер арқылы тұрғызу. Ол нүктелерінің координаталарын табу керек. Мұндай нүктелер шексіз көп болғандықтан бұл мүмкін емес деуге болады. Сондықтан функцияның графигі үлкен немесе аз дәлдікпен жуықтап бейнеленген. График тұрғызудың ең қарапайым әдісі координаталық нүктелер арқылы тұрғызу. Ол 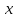 аргументіне мәндердің шекті саны берілгенінен тұрады, айталық, аргументіне мәндердің шекті саны берілгенінен тұрады, айталық, 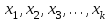 және функцияның таңдалған мәндерін қамтитын кесте құрастырылады. және функцияның таңдалған мәндерін қамтитын кесте құрастырылады.Кесте келесідей бейнеленеді: 1-кесте
Осындай кестені құрастыра отырып, біз  функциясының графигінде бірнеше нүктелерді белгілей аламыз. Содан кейін бұл нүктелерді тегіс сызықпен қоса отырып, функциясының графигінде бірнеше нүктелерді белгілей аламыз. Содан кейін бұл нүктелерді тегіс сызықпен қоса отырып,  функциясының графигінің жуық көрінісін аламыз. функциясының графигінің жуық көрінісін аламыз.Дегенмен, көп нүктелі сызба әдісі өте сенімсіз екенін атап өткен жөн. Шын мәнінде, графиктің белгіленген нүктелер арасындағы әрекеті және оның алынған экстремалды нүктелер арасындағы сегменттен тыс әрекеті белгісіз болып қалады. Бұл әдіс көбіне график тұрғызумен алғаш танысқанда қолданылады. Мысал 1.  функциясының графигін тұрғызу үшін аргументпен функцияның мәндерін кестеге жазайық. функциясының графигін тұрғызу үшін аргументпен функцияның мәндерін кестеге жазайық.2-кесте
Кестеге сәйкес бес нүкте 14-суретте көрсетілген. 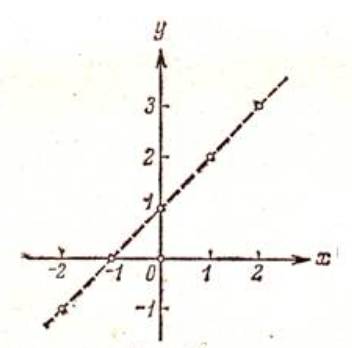 14-сурет Осы нүктелердің орналасуына сүйене отырып, ол функцияның графигі түзу болады деген қорытындыға келдік (14-суретте нүктелі сызықтармен көрсетілген). Бұл тұжырымды сенімді деп санауға бола ма деген сұрақ туындайды. Бұл тұжырымды растайтын қосымша тұжырымдамалар болмаса, оны сенімді деп санауға болмайды. Біздің ойымызды дәлелдеу үшін келесі функцияны қарастырайық: 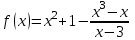 . .Есептеулер бұл функцияның -2, -1, 0, 1, 2 нүктелеріндегі мәндері жоғарыдағы кестемен сәйкес келеді. Бірақ бұл функцияның графигі мүлде түзу емес (15-суретте көрсетілген). Тағы бір мысал 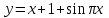 функциясы; оның мәндері жоғарыдағы кестеде сипатталған. функциясы; оның мәндері жоғарыдағы кестеде сипатталған.Бұл мысалдар оның «таза» түрінде бірнеше координаталық нүкте арқылы график тұрғызу әдісінің сенімсіз екенін көрсетеді. Сондықтан берілген функцияның графигін салу үшін, әдетте, келесідей әрекет ету керек. Алдымен бұл функцияның қасиеттері зерттеледі, оның көмегімен графиктің бейнесін салуға болады. Содан кейін функцияның бірнеше нүктелеріндегі мәндерін (оны таңдау функцияның қасиеттеріне байланысты) есептеу арқылы графиктің сәйкес нүктелері табылады. Және, ең соңында, осы функцияның қасиеттерін пайдалана отырып, салынған нүктелер арқылы қисық сызылады. 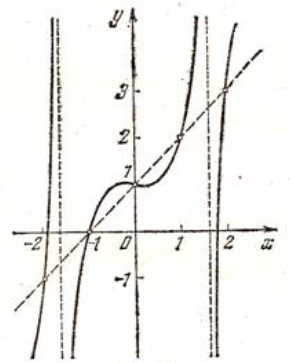 15-сурет Графиктің бейнесін салу үшін қолданылатын функциялардың кейбір (ең қарапайым және жиі қолданылатын) қасиеттерін кейін қарастырамыз, бірақ қазір графиктерді салудың кейбір жиі қолданылатын әдістерін талдаймыз. 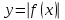 функциясының графигі. функциясының графигі.Көбінесе 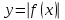 функциясының графигін тұрғызу қажет, мұндағы функциясының графигін тұрғызу қажет, мұндағы 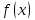 берілген функция. Санның абсолютті мәнін анықтамасы бойынша берілген функция. Санның абсолютті мәнін анықтамасы бойынша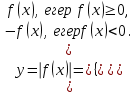 жазуға болады. Бұл  функциясының графигінен функциясының графигінен 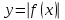 функциясының графигін келесідей алуға болады: Ординаталары теріс емес функциясының графигін келесідей алуға болады: Ординаталары теріс емес  функциясы графигінің барлық нүктелері өзгеріссіз қалдырылуы керек; кейін, теріс координаталары бар функциясы графигінің барлық нүктелері өзгеріссіз қалдырылуы керек; кейін, теріс координаталары бар  функциясының графигінің нүктелерінің орнына функциясының графигінің нүктелерінің орнына 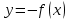 функциясының графигінің сәйкес нүктелерін салу керек (яғни бөлігі функциясының графигінің сәйкес нүктелерін салу керек (яғни бөлігі 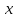 осінен төмен орналасқан осінен төмен орналасқан  функциясының графигі функциясының графигі 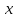 осіне қатысты симметриялы түрде көрсетілуі керек). осіне қатысты симметриялы түрде көрсетілуі керек).Мысал 2. 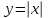 функциясының графигін салыңыз. функциясының графигін салыңыз.Шешуі: 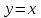 функциясының графигін (16а-сурет) алып, және сол графиктің бөлігін функциясының графигін (16а-сурет) алып, және сол графиктің бөлігін 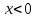 ( (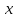 осінің астында жатқан) осінің астында жатқан) 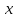 осіне қатысты симметриялы түрде көрсетеміз. Нәтижесінде осіне қатысты симметриялы түрде көрсетеміз. Нәтижесінде 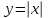 функциясының графигін аламыз (Cурет 16, ә). функциясының графигін аламыз (Cурет 16, ә).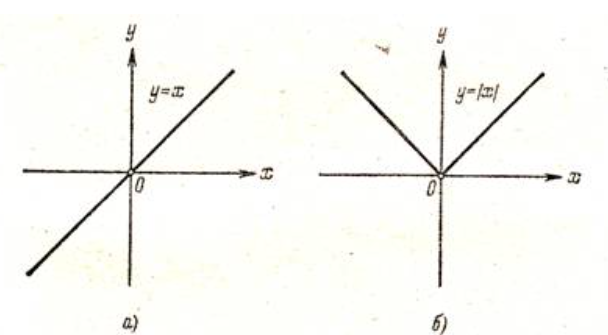 16-сурет Мысал 3. 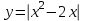 функциясының графигін салыңыз. функциясының графигін салыңыз.Алдымен 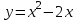 функциясының графигін салайық. Бұл функцияның графигі — парабола, оның тармақтары жоғары бағытталған, параболаның төбесінің координаталары функциясының графигін салайық. Бұл функцияның графигі — парабола, оның тармақтары жоғары бағытталған, параболаның төбесінің координаталары 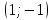 , оның графигі абсцисса осін 0 және 2 нүктелерінде қиып өтеді. , оның графигі абсцисса осін 0 және 2 нүктелерінде қиып өтеді. 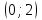 аралықта функция теріс мәндерді қабылдайды, сондықтан графиктің бұл бөлігі аралықта функция теріс мәндерді қабылдайды, сондықтан графиктің бұл бөлігі 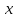 осіне қатысты симметриялы түрде көрсетіледі. 17-суретте осіне қатысты симметриялы түрде көрсетіледі. 17-суретте 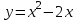 функциясының графигіне негізделген функциясының графигіне негізделген 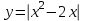 функциясының графигі салынған. функциясының графигі салынған.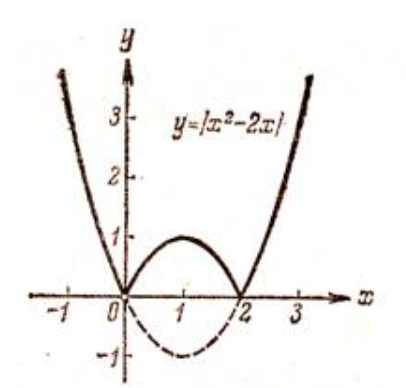 17-сурет 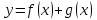 функциясының графигі. функциясының графигі. және және 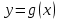 функцияларының графиктері берілген болса, функцияларының графиктері берілген болса, 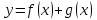 функциясының графигін салу есебін қарастырайық. функциясының графигін салу есебін қарастырайық.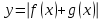 функцияның анықталу облысы функцияның анықталу облысы  және және 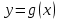 функцияларының екеуі де анықталған функцияларының екеуі де анықталған 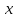 -тің барлық мәндерінің жиыны екенін ескерейік, яғни анықталу облысы -тің барлық мәндерінің жиыны екенін ескерейік, яғни анықталу облысы 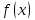 және және 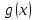 функцияларының анықталу облыстарының қиылысуы болып табылады. функцияларының анықталу облыстарының қиылысуы болып табылады.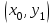 және және 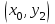 нүктелері нүктелері  және және 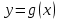 функцияларының графиктеріне тиесілі болсын, яғни функцияларының графиктеріне тиесілі болсын, яғни  , , 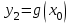 . Сонда . Сонда 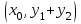 нүктесі нүктесі 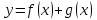 функциясының графигіне жатады (өйткені функциясының графигіне жатады (өйткені 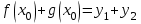 ), оның үстіне ), оның үстіне 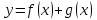 функциясының графигінің кез келген нүктесін осылайша алуға болады. функциясының графигінің кез келген нүктесін осылайша алуға болады.Сондықтан 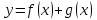 функциясының графигін функциясының графигін  және және 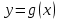 функцияларының графиктерінің әрбір функцияларының графиктерінің әрбір 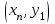 нүктесін нүктесін  функциясының графигінің функциясының графигінің  нүктесімен ауыстыруға болады, мұндағы нүктесімен ауыстыруға болады, мұндағы 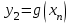 , яғни, , яғни,  графигінің әрбір графигінің әрбір 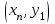 нүктесін нүктесін 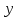 осі бойымен осі бойымен 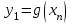 шамасына жылжыту арқылы. Бұл жағдайда шамасына жылжыту арқылы. Бұл жағдайда  және және 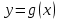 функцияларының екеуі де анықталған функцияларының екеуі де анықталған  нүктелері ғана қарастырылады. нүктелері ғана қарастырылады.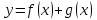 функциясының графигін салудың бұл әдісі функциясының графигін салудың бұл әдісі  және және 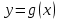 функцияларының графиктерін қосу деп аталады. функцияларының графиктерін қосу деп аталады.Мысал 4. Суретте 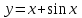 функция графигін салу үшін графикті қосу әдісін пайдаланыңыз. функция графигін салу үшін графикті қосу әдісін пайдаланыңыз.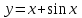 функциясының графигін салғанда функциясының графигін салғанда 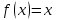 және және 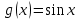 деп есептедік. Функцияның графигін салу үшін абсциссалары деп есептедік. Функцияның графигін салу үшін абсциссалары  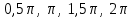 болатын нүктелерді таңдаймыз. болатын нүктелерді таңдаймыз.  мәндері таңдалған нүктелер бойынша есептеліп, нәтижелер кестеге орналастырылады. мәндері таңдалған нүктелер бойынша есептеліп, нәтижелер кестеге орналастырылады.3-кесте
Алынған нәтижелерге сүйене отырып, 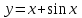 функциясының графигінің бейнесі болатын тегіс қисық сызықпен қосатын нүктелерді саламыз. функциясының графигінің бейнесі болатын тегіс қисық сызықпен қосатын нүктелерді саламыз.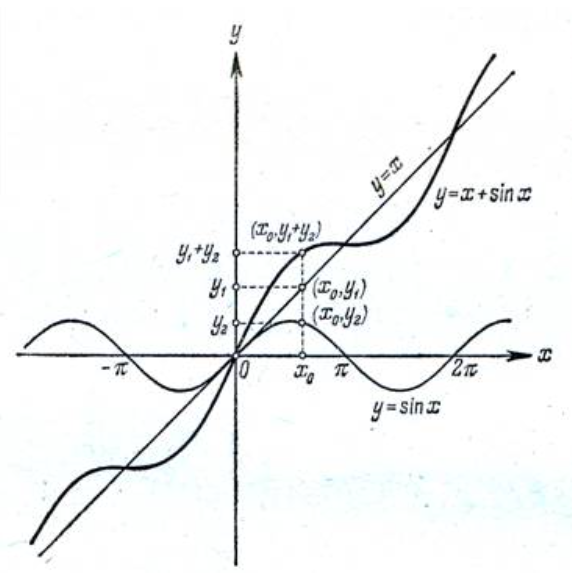 18-сурет |