уа. диплом2. Дипломды Жмыс таырыбы Функциялармен тедеулерді графиктерін трызуа координаттар дісін олдану
 Скачать 3.49 Mb. Скачать 3.49 Mb.
|
|
М. Өтемісов атындағы Батыс Қазақстан университеті Қорғауға жіберілді Каф. меңгерушісі _____ Маутеева С.М.... ДИПЛОМДЫҚ ЖҰМЫС Тақырыбы: «Функциялармен теңдеулердің графиктерін тұрғызуға координаттар әдісін қолдану» 5В010900 – Математика Орындаған: М-41 топ студенті Жалгасбаев Ж.К. Ғылыми жетекшісі: ф-м.ғ.к., аға оқытушы Кульжумиева А.А. О  рал 2022 ж. рал 2022 ж.МАЗМҰНЫ КІРІСПЕ 3 1 Негізгі мектепте координаттар әдісін қолданудың теориялық негіздері 6 1.1 Мектептегі координаттар әдісін зерттеудің негізгі ережелері 6 1.2 Координаталық әдіс тарихынан 7 1.3 Координаталар әдісімен есептерді шешу кезеңдері 9 1.4 Мектеп оқулықтарын талдау 10 Бірінші бөлім бойынша қорытынды 13 2 Функциялармен теңдеулердің графиктерін салу 15 2.1 Координаттық әдісті оқытатын есептер 15 2.2 Функцияның графигін координаталық әдіспен тұрғызу 24 2.3 Координаталық әдістің есеп шығаруда қолдануы 31 2.4 Координаталық әдіс арқылы теңдеудің графиктерін салу 37 Екінші бөлім бойынша қорытынды 43 ҚОРЫТЫНДЫ 44 ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 45 КІРІСПЕ Математикада есептерді шешудің әртүрлі әдістері қолданылады. Олар мектепте әртүрлі орын алады. Геометрияда көп қолданылатын әдіс синтетикалық әдіс болып саналады, ал басқа әдістерінің ішінде координаттар әдісі алгебрамен тығыз байланыстылығымен ерекшеленеді. Синтетикалық әдістің рақымына түйсігі, болжамдары, қосымша құрылыстары арқылы қол жеткізіледі. Координаталық әдіс мұны қажет етпейді: есептерді шешу көп жағдайда алгоритмделген, көп жағдайда шешімін іздеуді және шешуді жеңілдетеді. Бұл әдісті зерттеу мектеп математикасының ажырамас бөлігі деп сеніммен айтуға болады. Бірақ есептерді координаталық әдіспен шешу кезінде алгебралық есептеу шеберлігі қажет екенін және жоғары деңгейдегі тапқырлықты қажет етпейтінін ұмытпауымыз керек, бұл өз кезегінде оқушылардың шығармашылық қабілеттеріне теріс әсер етеді. Сондықтан студенттерге әртүрлі есептерді координаталық әдіспен шешуді үйренуге мүмкіндік беретін координаттар әдісін зерттеу әдістемесі қажет, бірақ бұл әдісті геометриялық есептерді шешудің негізгі әдісі ретінде көрсетпейді. Бұл таңдалған тақырыптың өзектілігін анықтайды:"негізгі мектеп геометриясының мектеп курсындағы координаттар әдісін зерттеу". Графиктер тұрғызудың координаталық әдісі бірнеше артықшылықтарға ие: • аналитикалық әдіске қарағанда қарапайым; • көрнекілік қасиетке ие. Әсіресе, шешімдер жоқ болғанда немесе түбірлерінің санын білу қажет болғанда. • эстетикалық әсер береді, көзге жағымды. Графиктер түрлі-түсті болуы керек. Бұл жауапты таңдауға көмектеседі. Функциялардың графиктерін құру мүмкіндігі өз алдына мақсат емес. Көбінесе график құру функцияларды зерттеумен байланысты. Дегенмен, графиктерді құру қажеттілігі аналитикалық есептеулерді қысқарту немесе жеңілдету, теңдеулер мен теңсіздіктердің шешімдерін табуды жеңілдетеді және көбінесе бір уақытта олар мұндай есептерді шешудің жалғыз әдісі болып табылады. Шешудің координаталық әдісі бірқатар ұғымдарды жақсы меңгеруге ықпал етеді: функциялар, теңдеулер мен теңсіздіктер түбірлері, теңдеулер жүйелері. Сонымен қатар, теңдеулерді координаталық жолмен шешу кезінде шамалар арасындағы функционалдық байланысты жақсы түсінуге көмектесетін функциялардың өсу және кему, тұрақтылық, функцияны нөлге айналдыру және т.б. қасиеттерімен байланыс орнатқан жөн. Функциялардың әрекетін және олардың графиктерін құруды зерттеу математиканың маңызды саласы болып табылады. Диаграммаларды құру әдістерін меңгеру көбінесе көптеген мәселелерді шешуге көмектеседі және кейде оларды шешудің жалғыз жолы болып табылады. Сонымен қатар, графикті құру мүмкіндігі үлкен тәуелсіз қызығушылық тудырады. Функциялардың графиктерін құруға байланысты материал орта мектепте емтиханға қойылатын талаптар тұрғысынан толық зерттелмеген. Сондықтан графиктерді құруға арналған тапсырмалар көбінесе оқушыларға қиындық туғызады. Графиктерден ақылға қонымды сандық жауаптар алу үшін графиктер әсіресе мұқият құрастырылуы керек. Жұмысты ұйымдастыру міндеті қарапайым функцияларды және олардың түрлендірулерін жылдам сызу дағдыларын қалыптастыратындай шешілуде. Графикалық дағдыларды қалыптастыру жұмысы 5-сыныптан басталады. Функциялардың әрекетін зерттеу және олардың графиктерін құру мектеп курсының маңызды бөлігі болып табылады. Диаграммаларды құру әдістерін жетік білу көбінесе күрделі есептерді шешуге көмектеседі, ал кейде оларды шешудің жалғыз құралы болып табылады. Сонымен қатар, функциялардың графигін тұрғызу қабілеті білім алушылардың өздеріне үлкен қызығушылық тудырады. Алайда, негізгі мектеп базасында бұл мәселеге қатысты материал ретсіз берілген, көптеген маңызды жайттар бағдарламаға енбеген, жеткіліксіз зерттелген. Зерттеу нысаны: Мектеп математика курсында білім алушылардың график тұрғызуды зерттеу процесі болып табылады. Зерттеу пәні. Мектептің математика курсында теңдеулер мен функциялардың графиктерін тұрғызудың координаттар әдісін зерттеу. Зерттеудің мақсаты. Теңдеулер мен функциялардың графиктерін тұрғызудың координаттар әдісін зерттеу және қолдану әдістемесін жасау. Зерттеу міндеттері: 1. Мектептегі координаттар әдісін зерттеудің негізгі ережелері және мақсаттарын, тікбұрышты координаталар жүйесінің тарихын анықтау; 2. Есептерді алгебралық және геометриялық координаттар әдісімен шешу үшін кезеңдерін белгілеп, мысалдар қарастыру; 3. Ғылыми әдістемелік әдебиеттерге және мектеп оқулықтарына шолу жасау. 4. Координаталық әдіс арқылы функция мен теңдеулердің графиктерін тұрғызуды қолданатын есептерді шешу мысалдарын қарастыру. Жұмыс мақсаттарына жету, гипотезаны тексеру және жоғарыда аталған міндеттерді шешу үшін келесі әдістер қолданылды: – координаттар әдісіне қатысты математика бойынша бағдарламаны, оқу құралдарын, әдістемелік материалдарды талдау; – білім беру процесінің барысын, оқушылардың қызметін бақылау. Зерттеудің теориялық маңыздылығы теңдеулер мен функциялардың графиктерін тұрғызудың координаттар әдісін қолданып есептердің мысалдарын қарастырылуында. Зерттеудің практикалық маңыздылығы. Теңдеулер мен функциялардың графиктерін тұрғызудың координаттар әдісін мектептің математика курсында әр сыныптың әр деңгейлі оқушыларға және ЖОО студенттеріне көмекші құрал ретінде пайдалануға болады. Қорғауға мыналар ұсынылады: теңдеулер мен функциялардың графиктерін тұрғызудың координаттар әдісін қолдану бойынша әдістемелік ұсыныстар. Дипломдық жұмыс кіріспеден, екі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады. Кіріспеде зерттеудің негізгі сипаттамалары – өзектілігі, проблемасы, объектісі, пәні, мақсаты, міндеттері және зерттеу әдістері тұжырымдалған. Пайдаланылған әдебиеттер тізімі 32 әдебиеттен тұрады. Негізгі тәжірибелік база А.Тайманов атындағы №34 мектеп гиназиясы болды. 1 Негізгі мектепте координаттар әдісін қолданудың теориялық негіздері Мектептегі координаттар әдісін зерттеудің негізгі ережелері Координаталық әдісті қолданып есептер шығару әдістері біркелкі. Элементар геометрияда оқушылар әрбір есептің арнайы шешімін іздеуі керек, ал есептер кез келген есептерге оңай бейімделетін белгілі бір алгоритм бойынша шешеді. Координаталық әдістің басты құндылығы мынада, бұл әдісті алгебрадан геометрияға көшіру арқылы біз есептерді шешудің тамаша жалпы тәсілін табамыз. Сондай-ақ, егер біз бұл әдісті қолданатын болсақ, онда күрделі кеңістіктік бейнелерді визуалды бейнелеуге жүгінудің қажеті жоқ. Координаталық әдісті зерттеу келесі мақсаттарды көздейді: - білім алушыларға есептер шығарудың және бірқатар теоремаларды дәлелдеудің жаңа әдісін беру; -координаталық әдіс арқылы геометрия мен алгебра арасындағы тығыз байланысты көрсету; - оқушылардың есептеу және графикалық мәдениетін дамытуға ықпал ету. Мектепте координаталық әдісті оқып үйрену және оны әртүрлі математикалық есептерді шығаруға қолдануға үйрету бірнеше кезеңнен тұрады. Бірінші кезеңде 5-6-сыныптарда жақсы өңделген және геометрия курсында жүйеленген негізгі ұғымдық аппарат енгізіледі. 5-сыныпта оқушылар координаталық сәулемен танысады, ол кейін теріс сандарды оқығанда координаталық түзумен толықтырылады. Ал 6-сыныпта рационал сандар енгізілгеннен кейін оқушылар координаталық жазықтықты зерттейді. Екінші кезеңде оқушылар түзу мен шеңбердің теңдеулерімен танысады. Бұл ұғымдар алгебрада да, геометрияда да әртүрлі мазмұндық мақсатпен зерттейді, сондықтан оқушылар көбінесе олардың арасындағы байланысты көрмейді, сондықтан әдістің мәнін нашар түсінеді. Сонымен VII сынып алгебра курсында негізгі функциялардың графиктері функцияның аналитикалық спецификациясынан координаталары есептелетін нүктелер қатарын құру арқылы енгізіледі. Геометрия курсында түзу мен шеңбердің теңдеуі геометриялық сипаттамалық қасиеттер негізінде белгілі бір қасиетке ие нүктелер жиыны ретінде енгізіледі (тең арақашықтық 2 нүктеден – түзу үшін, бір нүктеден – шеңбер үшін). Есептер шығаруда координат әдісінің өзін қолдануды үйрену 9-сыныптың геометрия курсында өтеді. Ол үшін алдымен әдісті қолданудың негізгі кезеңдері ашылады, содан кейін бірқатар есептердің мысалында координаталық әдістің тікелей қолданылуы көрсетіледі. 10-сыныпта координаталық әдіс кеңістікте оқытыла бастайды. Көптеген формулалар мен ережелер қосылды, тапсырмалардың жаңа түрлері пайда болады [3,4]. Бірақ координат әдісі негізгі әдіс емес. Шарыгин И.Ф. бұл әдістің қауіптілігін атап өтті. Оқу үлгерімі шамалы оқушыларға келетін болсақ, «бұл топта көбіне дұрыс есептемейтін, формулаларды түсініп, есте сақтау қиын балалар кездеседі. Бұл балалар үшін математика жалпы математикалық дамудың кемшіліктерін толтыра алатын пәнге айналуы мүмкін. Керісінше, оларға қосымша салмақ түсіреді. Координаталық әдіс зерттелетін геометриялық жағдайдың геометриялық мәнін шетке қалдырады. Берілген нақты мәселені шешетін орындаушы тәрбиеленеді. Аз емес, бірақ көп емес. Зерттеуші математикке өте қажет геометриялық, тіпті математикалық интуиция дамымайды» [8]. Координат әдісі – нүктелердің немесе денелердің орнын санау немесе басқа белгілер арқылы анықтау тәсілі. Түзудегі, жазықтықтағы, кеңістіктегі, беттегі және т.б. нүктелердің (денелердің) орнын анықтайтын сандар (таңбалар) оның координаталары деп аталады. Зерттеудің мақсаты мен сипатына байланысты әртүрлі координат жүйелері таңдалады. Координаталар жүйесі – бұл нүктенің немесе дененің орнын сандар немесе басқа белгілер арқылы анықтау тәсілі. Белгілі бір нүктенің орнын анықтайтын сандар немесе белгілер жиыны осы нүктенің координаталары деп аталады. Ең жиі қолданылатын координаттар жүйесі декарттық координаттар жүйесі. Есептерді шешу әдісі ретіндегі координаталар әдісінің мәні мынада: фигураларды теңдеулер арқылы қою және координаттардағы әртүрлі геометриялық қатынастарды өрнектеу арқылы геометриялық есепті алгебра арқылы шешуге болады. Координаталарды пайдалана отырып, алгебралық және аналитикалық қатынастар мен фактілерді геометриялық түрде түсіндіруге болады және осылайша геометрияны алгебралық есептерді шешуге қолдануға болады. Координат әдісі әмбебап әдіс болып табылады. Ол алгебра мен геометрия арасындағы тығыз байланысты қамтамасыз етеді, олар біріктірілген кезде олар бөлек қалса бере алмайтын «бай жемістер» береді. Мектептегі геометрия курсына келетін болсақ, кейбір жағдайларда координаттар әдісі дәлелдемелерді құруға және көптеген есептерді таза геометриялық әдістерге қарағанда ұтымдырақ, әдемі шешуге мүмкіндік береді деп айта аламыз. Координаталар әдісі бір геометриялық күрделілікпен байланысты. Бір есеп координаттар жүйесінің таңдауына байланысты басқа аналитикалық бейнені алады. Жеткілікті тәжірибе ғана ең қолайлы координаттар жүйесін таңдауға мүмкіндік береді [1]. 1.2 Координаталық әдіс тарихынан Қазіргі уақытта ғылымның әртүрлі салаларындағы мамандардың өте көп саны жазықтықтағы тікбұрышты декарттық координаттар туралы түсінікке ие, өйткені бұл координаттар графиктің көмегімен бір шаманың екіншісіне тәуелділігін суреттеуге мүмкіндік береді. "Декарттық координаттар" атауы бұл координаттарды Декарт ашқан деген жалған ойға әкеледі. Шындығында тікбұрышты координаттар біздің дәуірімізге дейін геометрияда қолданылған. Александрия мектебінің ежелгі математигі Аполлоний Пергский (б. з. д. III-II ғасырда өмір сүрген) қазірдің өзінде тікбұрышты координаттарды қолданды. Ол сол кезде белгілі қисықтарды: Параболаны, гиперболаны және эллипсті анықтап, зерттеді. Аполлоний оларды теңдеулермен анықтады:  (парабола) (парабола) (гипербола) (гипербола) (p және q оң болатын эллипс) (p және q оң болатын эллипс)Ол, әрине, теңдеулерді осы геометриялық формада жазған жоқ, өйткені ол кезде әлі алгебралық символизм болған жоқ, бірақ геометриялық ұғымдарды қолдана отырып теңдеулерді сипаттады; у2 оның терминологиясында у жағы бар квадраттың ауданы бар; px - p және х жақтары бар тіктөртбұрыштың ауданы және т.б. қисықтардың атаулары осы теңдеулермен байланысты. Парабола грек тілінде теңдікті білдіреді: квадраттың ауданы у2 тіктөртбұрыштың px ауданына тең. Гипербола грекше артық дегенді білдіреді: у2 квадратының ауданы тіктөртбұрыштың рх ауданынан асып түседі. Грек тіліндегі Эллипс кемшілікті білдіреді:шаршының ауданы тіктөртбұрыштың ауданынан аз. Декарт белгілерді таңдау ережелерін енгізу арқылы тікбұрышты координаттарға өте маңызды жақсарту енгізді. Бірақ ең бастысы, тікбұрышты координаттарды қолдана отырып, ол геометрия мен алгебраны байланыстыра отырып, жазықтықта аналитикалық геометрияны құрды. Айта кету керек, Декартпен бір уақытта аналитикалық геометрияны және басқа француз математигі ферманы салған. Аналитикалық геометрияның мәні, ең алдымен, геометрия мен алгебра арасында тығыз байланыс орнатқандығында. Декарт кезінде математиканың осы екі саласы жетілдірудің жоғары деңгейіне жетті. Бірақ олардың мыңдаған жылдар бойы дамуы бір-біріне тәуелсіз жүрді және олардың арасында аналитикалық геометрия пайда болған кезде тек әлсіз байланыс байқалды. Координаттар сандардың көмегімен кеңістіктің немесе жазықтықтың кез келген нүктесінің орнын анықтауға мүмкіндік береді. Бұл әр түрлі фигураларды сандардың көмегімен жазып, "шифрлауға" мүмкіндік береді. Координаттар арасындағы қатынастар көбінесе бір нүктені емес, нүктелердің белгілі бір жиынтығын (жиынтығын) анықтайды. Мысалы, егер абсцисса ординатқа тең болатын барлық нүктелерді, яғни координаталары  теңдеуін қанағаттандыратын нүктелерді атап өтсек, онда біз түзу сызық аламыз - бірінші және үшінші координаталық бұрыштардың бисекторлары. Кейде "нүктелер жиынтығының" орнына "нүктелердің геометриялық орны"дейді. Мысалы, координаттары  қатынасын қанағаттандыратын нүктелердің геометриялық орны-жоғарыда айтылғандай, бірінші және үшінші координаталық бұрыштың бисекторлары. Бір жағынан алгебра мен екінші жағынан геометрия арасындағы байланысты орнату математикадағы революция болды. Ол математиканы біртұтас ғылым ретінде қалпына келтірді, оның жеке бөліктері арасында "Қытай қабырғасы" жоқ. қатынасын қанағаттандыратын нүктелердің геометриялық орны-жоғарыда айтылғандай, бірінші және үшінші координаталық бұрыштың бисекторлары. Бір жағынан алгебра мен екінші жағынан геометрия арасындағы байланысты орнату математикадағы революция болды. Ол математиканы біртұтас ғылым ретінде қалпына келтірді, оның жеке бөліктері арасында "Қытай қабырғасы" жоқ. 1-сурет 1.3 Координаталар әдісімен есептерді шешу кезеңдері Есептерді алгебралық және геометриялық координаттар әдісімен шешу үшін 3 кезең орындалуы керек: Тапсырманы координаттық (Талдамалық) тілге аудару; Аналитикалық өрнекті түрлендіру; кері аударма, яғни координаталық тілден тапсырма тұжырымдалған тілге аудару. Мысалы, алгебралық және геометриялық есептерді қарастырып, координаталық әдіспен шешу кезінде осы 3 кезеңнің орындалуын суреттейміз. №1.  теңдеулер жүйесінің қанша шешім бар? Шешуі: 1 кезең: геометриялық тілде берілген есепте осы теңдеулермен берілген фигуралардың қанша қиылысу нүктелері бар екенін табу керек. Біріншісі-шеңбердің теңдеуі, оның басында центрі және радиусы 1, ал екіншісі-параболалық теңдеу. 2 кезең: шеңбер мен параболаның құрылысы; олардың қиылысу нүктелерін табу. 3 кезең: шеңбер мен параболаның қиылысу нүктелерінің саны қойылған сұрақтың жауабы болып табылады. №2. Осы екі нүктенің әрқайсысының қашықтығы тең болатын көптеген нүктелерді табыңыз. Біз координаталар жүйесін таңдаймыз, сондықтан 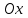 осі осі 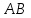 сызығымен сәйкес келеді, ал сызығымен сәйкес келеді, ал 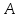 нүктесі координаталардың басы болады. нүктесі координаталардың басы болады.Бұдан әрі  , содан кейін таңдалған координаттар жүйесінде , содан кейін таңдалған координаттар жүйесінде  және және  делік. делік.  нүктесі нүктесі  немесе, сол сияқты, немесе, сол сияқты,  болғанда ғана қажетті жиынға жатады. болғанда ғана қажетті жиынға жатады. Координаталық жазықтықтың бір нүктесінен екіншісіне дейінгі қашықтық формуласын қолдана отырып, алатынымыз  , ,  . Сонда . Сонда   теңдігі және есепте берілген жағдайдың алгебралық моделі. Бұл оны шешудің бірінші кезеңін аяқтайды (мәселені координаталық тілге аудару). теңдігі және есепте берілген жағдайдың алгебралық моделі. Бұл оны шешудің бірінші кезеңін аяқтайды (мәселені координаталық тілге аудару).Екінші кезеңде алынған өрнекті түрлендіру жүзеге асырылады, нәтижесінде біз  қатынасын аламыз. қатынасын аламыз.Үшінші кезеңде теңдеудің тілін геометриялық тілге аудару жүзеге асырылады. Алынған теңдеу –  осіне параллель және осіне параллель және 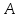 нүктесінен қашықтыққа, нүктесінен қашықтыққа,  яғни яғни 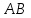 кесіндісіне орта перпендикуляр орналасқан түзудің теңдеуі. кесіндісіне орта перпендикуляр орналасқан түзудің теңдеуі. |
