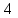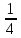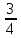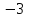уа. диплом2. Дипломды Жмыс таырыбы Функциялармен тедеулерді графиктерін трызуа координаттар дісін олдану
 Скачать 3.49 Mb. Скачать 3.49 Mb.
|
|
2.3 Координаталық әдістің есеп шығаруда қолдануы График деп әртүрлі екі шаманың арасындағы тәуелділікті айтады, ол координаталық жазықтықта сызықпен кескінделеді. 2.1.1 Алма ағашының 1 дм3 көлемінің массасы 0,4 кг. Алма ағашының 2 дм3, 3 дм3, 4 дм3, 5 дм3 көлемінің массасын тауып, оның графигін сызайық. Алма ағашының көлемімен массасының қатынасын пайдаланып, кестені толтырайық. 4-кесте
Тікбұрышты координаталар жүйесін сызып, абсцисса осіне алма ағашының көлемінің мәндерін, ал ординаталар осіне сәйкесінше массасының мәндерін белгілеп, 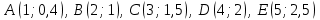 нүстелерін аламыз. Белгіленген нүктелерді кесінділермен қоссақ, алма ағашының массасының оның көлеміне тәуелділік графигі салынады. нүстелерін аламыз. Белгіленген нүктелерді кесінділермен қоссақ, алма ағашының массасының оның көлеміне тәуелділік графигі салынады.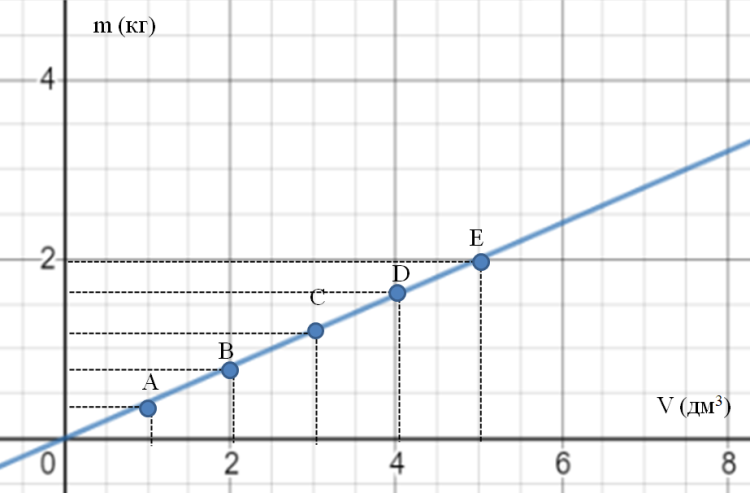 19-сурет 2.1.2 Жаяу жүргінші 6 км/сағ жылдамдықпен 2 сағат жүріп, кейін 1,5 сағат демалды, қалған 2,5 сағатта 5 км/сағ жылдамдықпен жүрді. Жаяу жүргінші жүрген жолының кестесін құрып, графигін сызайық. 5-кесте
Жаяу жүргінші демалғаннан кейін, оның жылдамдығы өзгеріп, 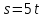 формуласымен есептеліп бастайды. Енді кестеде көрсетілген координаталары бойынша графикте нүктелерді белгілейік. формуласымен есептеліп бастайды. Енді кестеде көрсетілген координаталары бойынша графикте нүктелерді белгілейік.ОА кесіндісі жаяу жүргіншінің 6 км/сағ жылдамдықпен 2 сағат жүргеніне сәйкес келеді. АВ кесіндісі бұл жаяу жүргіншінің демалу уақытына сәйкес келеді, көріп отырғандай бұл кесінді абсциссалар осіне параллель. ВС кесіндісі қозғалыстың соңғы бөлігіне сәйкес келеді. Егер козғалыс графигі берілсе, уақытқа сәйкес жүрген жолды табуға болады, және керісінше жүрген жолдан ұанша уақыт жойғанын білуге болады. 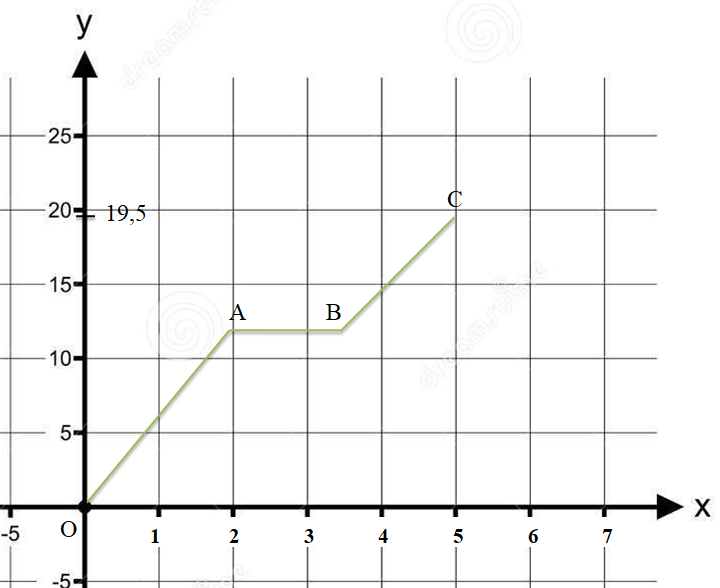 20-сурет Графиктер бойынша, жолдың уақытқа байланысты өзгерісін, температураның уақытқа байланысты өзгерісін, көлемнің температураға немесе қысымға бойынша өзгерісін, заттың құнының оның санына және бағасына тәуелділігін, т.б. білуге болады. 2.1.3 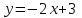 формуласымен берілген функция үшін аргументтің берілген мәндеріне сәйкес функцияның мәндерін тауып, кестені толтырып, график сызыңдар. формуласымен берілген функция үшін аргументтің берілген мәндеріне сәйкес функцияның мәндерін тауып, кестені толтырып, график сызыңдар.6-кесте
Шешуі. 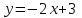 функцияның аргументін қолданып, функция мәндерін табайық. Есептегі графиктің аргументі функцияның аргументін қолданып, функция мәндерін табайық. Есептегі графиктің аргументі 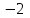 -ге тең болғандағы мәнін табайық. -ге тең болғандағы мәнін табайық.Ол үшін 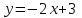 функциясындағы функциясындағы 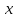 -тің орнына аргумент мәнін қоймыз: -тің орнына аргумент мәнін қоймыз: 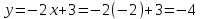 ; ;Қалған аргументтерді орнына қойып, функцияның мәндерін барлығын табамыз: 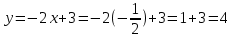 ; ;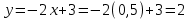 ; ;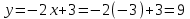 ; ;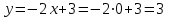 ; ;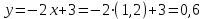 . .Шыққан сандарды кестеге жазайық: 7 -кесте
График функциясынан 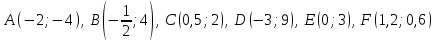 нүкте координаттарын алдық. Сәйкесінше, график сызайық. нүкте координаттарын алдық. Сәйкесінше, график сызайық.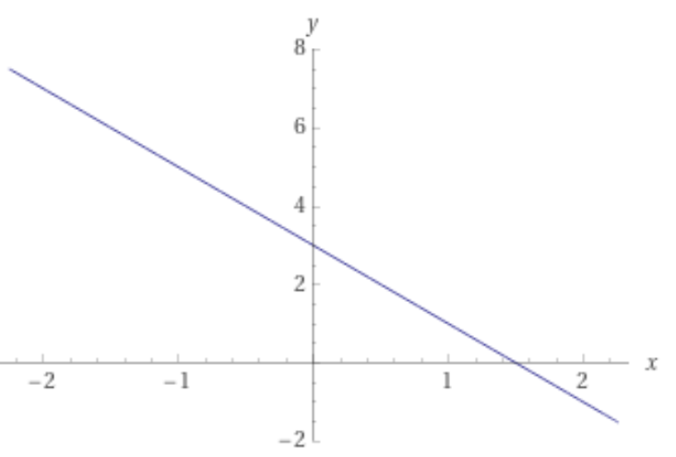 21-сурет 2.1.4 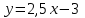 функциясының сәйкес аргумент пен мәндер жиынын кестеге толтырып, графигін көрсетіңіз. функциясының сәйкес аргумент пен мәндер жиынын кестеге толтырып, графигін көрсетіңіз.4-кесте
Шешуі: 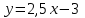 функцияның аргументтерін қолданып, функция мәндерін табайық. функцияның аргументтерін қолданып, функция мәндерін табайық.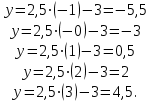 Сонда бізде 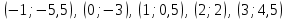 нүктелерін косып, түзу аламыз. Шыққан түзу нүктелерін косып, түзу аламыз. Шыққан түзу 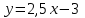 (22-сурет) функциясының графигі. (22-сурет) функциясының графигі.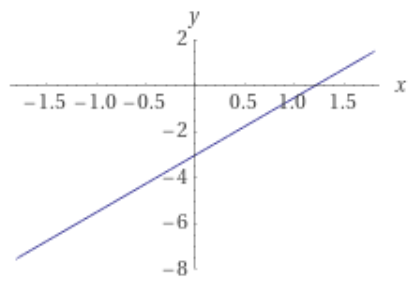 22-сурет 2.1.5 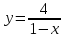 формуласымен берілген функцияның графигін формуласымен берілген функцияның графигін 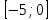 аралығында сызайық. аралығында сызайық.Ол үшін 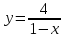 функциясының аргументтің функциясының аргументтің 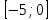 аралығындағы мәндерінің кестесін құру керек: аралығындағы мәндерінің кестесін құру керек:5-кесте
Нүктелерді сызықпен қоссақ, 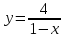 функциясының координаталық жазықтықтағы графигі салынады. функциясының координаталық жазықтықтағы графигі салынады.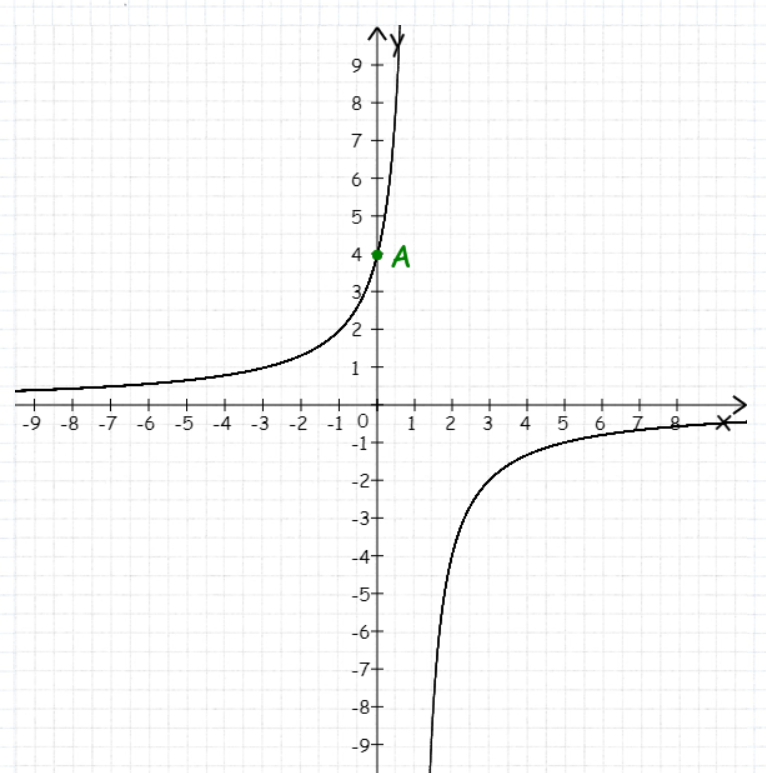 23-сурет Графиктегі нүктелердің координаттары неғұрлым жиі (көп) болса, график соғұрлым дәлірек болып есептеледі. 2.1.6 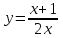 формуласымен берілген функцияның графигін формуласымен берілген функцияның графигін  аралығында сызайық. аралығында сызайық.Шешуі: Ол үшін 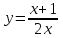 функциясының аргументтің функциясының аргументтің  аралығындағы мәндерінің кестесін құру керек: аралығындағы мәндерінің кестесін құру керек:5-кесте
Нүктелерді сызықпен қоссақ, 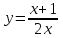 функциясының координаталық жазықтықтағы графигі салынады. функциясының координаталық жазықтықтағы графигі салынады.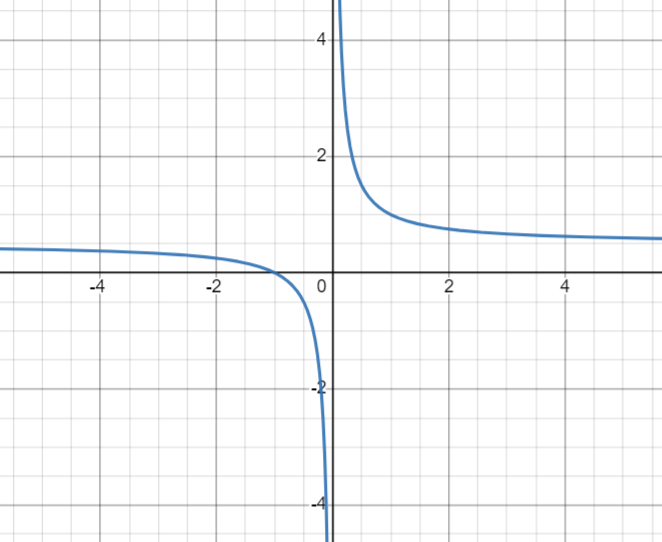 24-сурет 2.1.7 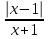 формуласымен берілген функцияның графигін формуласымен берілген функцияның графигін 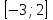 аралығында сызайық. аралығында сызайық.Шешуі: Ол үшін 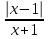 функциясының аргументтің функциясының аргументтің 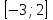 аралығындағы мәндерінің кестесін құру керек: аралығындағы мәндерінің кестесін құру керек:6-кесте
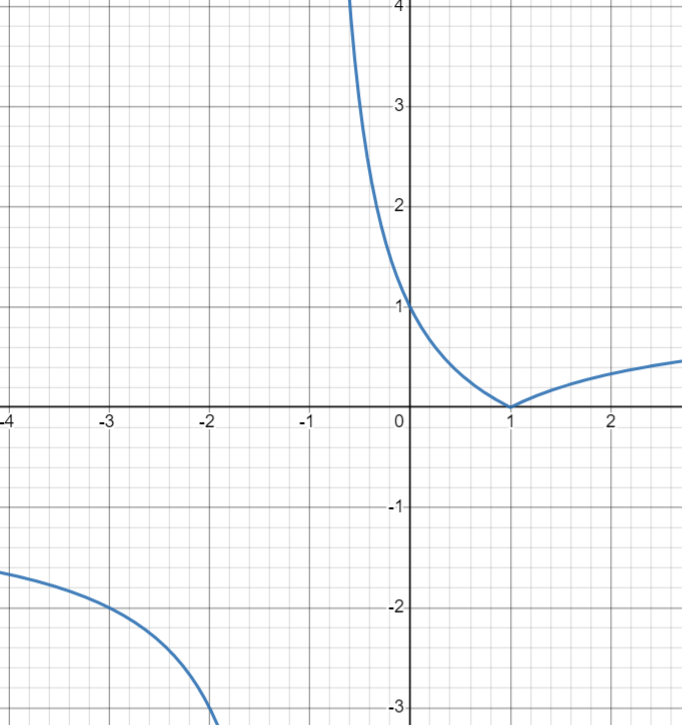 25-сурет Нүктелерді сызықпен қоссақ, 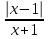 функциясының координаталық жазықтықтағы графигі салынады. функциясының координаталық жазықтықтағы графигі салынады.2.4 Координаталық әдіс арқылы теңдеудің графиктерін салу 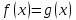 теңдігін координаталық әдіс арқылы шешу үшін теңдігін координаталық әдіс арқылы шешу үшін  және және 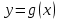 функцияларының графиктерін салу керек. Қиылысатын нүктелердің абсциссалары теңдеудің түбірі болады. функцияларының графиктерін салу керек. Қиылысатын нүктелердің абсциссалары теңдеудің түбірі болады.Бұл әдісті қолдана отырып, теңдеудің түбірлерінің санын білуге, түбірдің мәнін болжауға, түбірлердің шамамен немесе нақты мәндерін анықтауға болады. Кейбір жағдайларда функциялардың графиктерін құру қажет емес, өйткені функциялардың кейбір қасиеттерін қолдануға болады. Мысалға,  , , 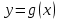 функциялары берілген және олардың бірі өспелі, екіншісі кемімелі. Бұл жағдайда функциялары берілген және олардың бірі өспелі, екіншісі кемімелі. Бұл жағдайда 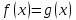 теңдеуінің бір түбірі бар немесе түбірі мүлде болмауы мүмкін. теңдеуінің бір түбірі бар немесе түбірі мүлде болмауы мүмкін.3.1.1  теңдеуін координаталық әдіспен шешіңіз. теңдеуін координаталық әдіспен шешіңіз.Шешуі: 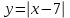 және және  функцияларының графиктерін бір координаталық жазықтыққа салайық: функцияларының графиктерін бір координаталық жазықтыққа салайық: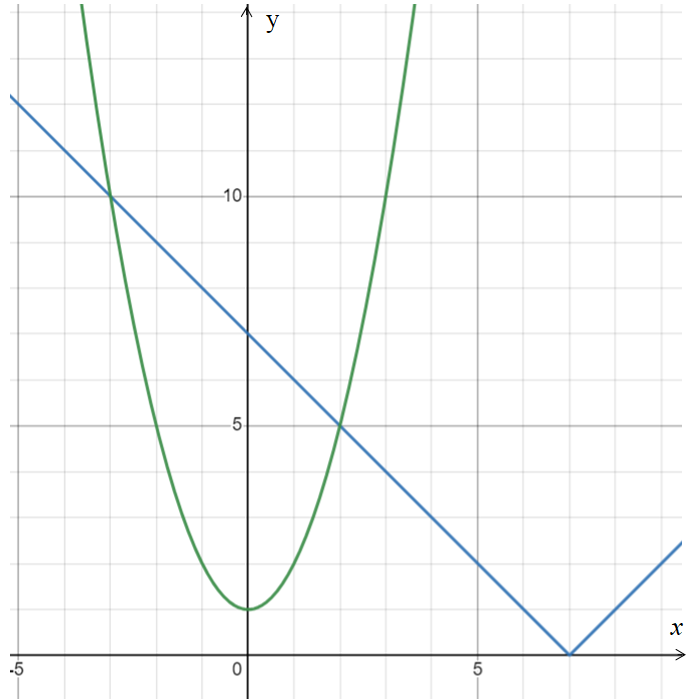 26-сурет. Көк түсті қисық – 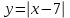 , жасыл түсті – , жасыл түсті –  . .Бұл графиктер 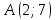 және және 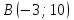 нүктелерінде қиылысады. Демек теңдеудің түбірлері: нүктелерінде қиылысады. Демек теңдеудің түбірлері: 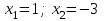 . .Жауабы: 1; 4. 3.1.2 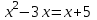 теңдеуін координаталық әдіспен шешіңіз. теңдеуін координаталық әдіспен шешіңіз.Шешуі: 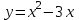 және және 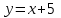 функцияларының графиктерін бір координаталық жазықтыққа салайық: функцияларының графиктерін бір координаталық жазықтыққа салайық: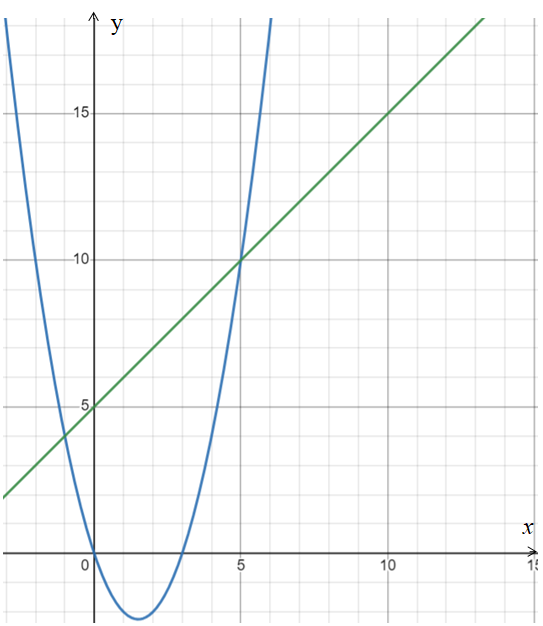 27-сурет. 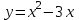 – көк түсті, – көк түсті,  – жасыл түсті график. – жасыл түсті график.27-суреттен көрініп тұрғандай екі график 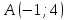 және және  нүктелерінде қиылысады. Осылайша теңдеудің түбірлері нүктелерінде қиылысады. Осылайша теңдеудің түбірлері 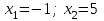 . .Жауабы: 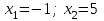 . .3.1.3 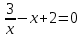 теңдеуін координаталық әдіспен шешіп көрейік. теңдеуін координаталық әдіспен шешіп көрейік.Әрине, ортақ бөлгішке келтіріп алынған теңдеудің түбірін таба аламыз, бірақ графикалық жолмен координаталық әдіс арқылы шешейік. Теңдеуді екіге бөліп жазайық: – 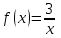 – графигі гипербола; – графигі гипербола;– 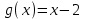 – графигі түзу. – графигі түзу.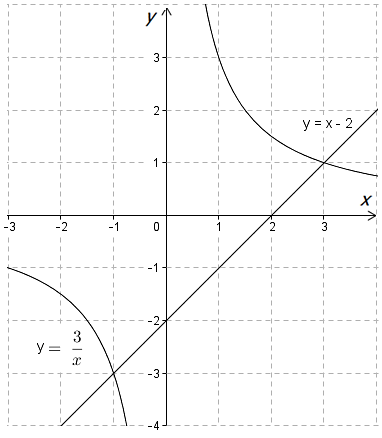 28-сурет Жауабы: теңдеудің түбірлері 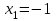 және және 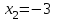 . .Енді 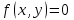 екі айнымалысы бар теңдеуді қарастырайық. Бұл теңдеудің шешімі екі айнымалысы бар теңдеуді қарастырайық. Бұл теңдеудің шешімі 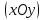 координаталық жазықтықта бейнелеуге болатын координаталық жазықтықта бейнелеуге болатын 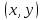 нүктелер жұбының жиыны болады. нүктелер жұбының жиыны болады.3.1.4 Мысал ретінде 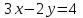 қарапайым сызықтық теңдеуін алайық. Теңдеудің жалпы шешімін – қарапайым сызықтық теңдеуін алайық. Теңдеудің жалпы шешімін – 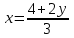 -ті шығарып алдық. Оны координаталық жазықтықта бейнелеп көрейік: -ті шығарып алдық. Оны координаталық жазықтықта бейнелеп көрейік:Графиктің барлық нүктелері біздің теңдеудің шешімдері болады. Мысалы, 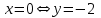 . Және . Және 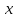 және және 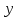 шешімдерінің дәл бірдей жұптарын береді. шешімдерінің дәл бірдей жұптарын береді.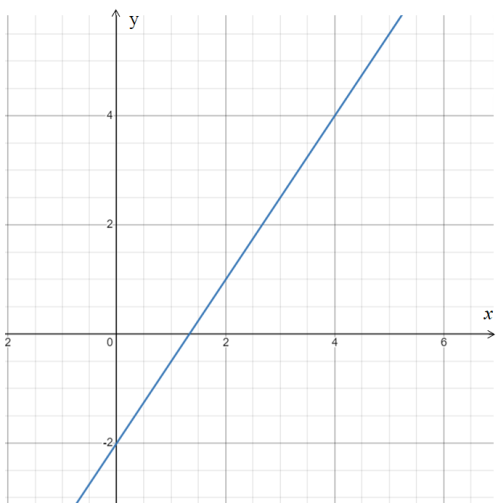 29-сурет. 3.1.5 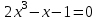 теңдеуінің түбірлерін табыңыз. теңдеуінің түбірлерін табыңыз.Теңдеудің бір бөлігін оң жаққа шығарып, екі функцияға оңай бөлуге болатындай етіп 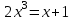 түрлендіреміз. түрлендіреміз. 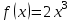 – кубтық парабола, – кубтық парабола, 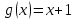 – қарапайым түзу. – қарапайым түзу.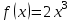 және және 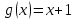 функцияларын координаталық жазықтыққа бейнелейміз (30-сурет). функцияларын координаталық жазықтыққа бейнелейміз (30-сурет).Екі график бір нүктеде қиылысады, теңдеудің түбірі – 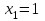 . .3.1.6  теңдеуінің түбірлерін табыңыз. теңдеуінің түбірлерін табыңыз.Шешуі: Теңдеудің бір бөлігін оң жаққа шығарып, екі функцияға оңай бөлуге болатындай етіп  түрлендіреміз. түрлендіреміз. 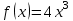 – кубтық парабола, – кубтық парабола, 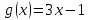 – түзу. – түзу.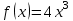 және және 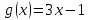 функцияларын координаталық жазықтыққа бейнелейміз (31-сурет). функцияларын координаталық жазықтыққа бейнелейміз (31-сурет). 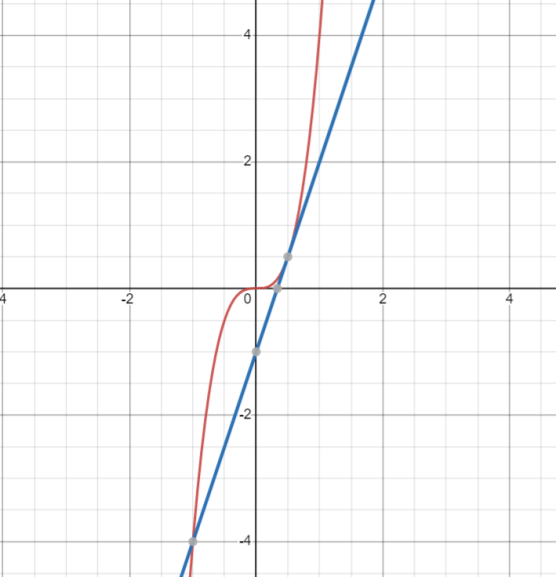 30-сурет 31-сурет Жоғардағы қаралған есептердің барлығын әрине басқа жолмен және одан да жылдам шығаруға болады. Бірақ кей есептер үшін координаталық әдіс ең қолайлы және әмбебап тәсіл. 3.1.7 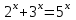 теңдеуінің түбірлерін табыңыз. теңдеуінің түбірлерін табыңыз.Шешуі: Бір қарағанда теңдеудің түбірі 1-ге тең екені анық: 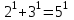 . Бірақ та шешімді математикалық түрде шешу қиынға соғады. Осындай кезде координаталық әдіс көмектеседі: . Бірақ та шешімді математикалық түрде шешу қиынға соғады. Осындай кезде координаталық әдіс көмектеседі:Берілген теңдеуді екі функцияға бөліп жазайық: 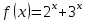 , , 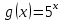 – көрсеткіштік функциялар. – көрсеткіштік функциялар.Екі графиктің қиылысуы нүктелерінің абсциссалары теңдеудің түбірі болатынын ұмытпайық. 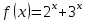 , , 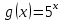 функцияларын координаталық жазықтыққа бейнелейміз (3-сурет). функцияларын координаталық жазықтыққа бейнелейміз (3-сурет). Көріп тұрғанымыздай, екі график бір нүктеде қиылысады екен, демек теңдеудің бір түбірі бар және ол 1-ге тең. Жауабы: -1; Қай график қай түсті екенін табу үшін, координаталар (7-кесте) әдісін қолданамыз: Процессті жылдамдату үшін тек бір функцияны ғана аламыз. 7-кесте
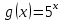 графигігің абсциссасы графигігің абсциссасы 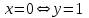 тең болу керек, бұл күлгін график. тең болу керек, бұл күлгін график.Жауабы: 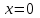 . . 32-сурет. Көк түсті график – 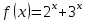 , күлгін түсті , күлгін түсті 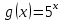 3.1.8  теңдеуінің шешімін табыңыз. теңдеуінің шешімін табыңыз.Шешуі: Бұл есеп дәл 3.1.5 есепке ұқсайды. Және дәл солай шығарылады. 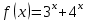 және және 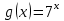 функциялары – көрсеткіштік. Функцияларды бір координаталық жазықтыққа салып, бейнелейік (-сурет). функциялары – көрсеткіштік. Функцияларды бір координаталық жазықтыққа салып, бейнелейік (-сурет).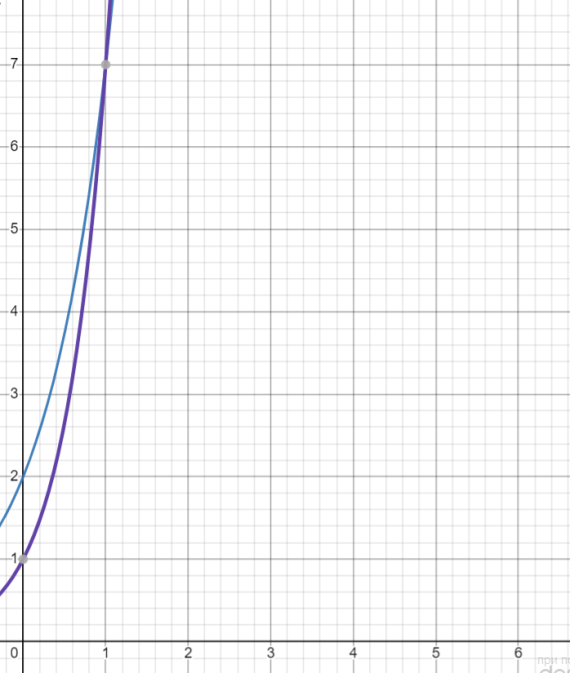 33-сурет. Қиылысу нүктесінің абсциссасы 1, демек теңдеудің түбірі де 1-ге тең. Жауабы: 1. 3.1.8 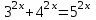 теңдеуінің түбірлерін табыңыз. теңдеуінің түбірлерін табыңыз.Шешуі: Бір қарағанда теңдеудің түбірі 1-ге тең екені анық: 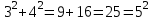 . Бірақ та шешімді табу үшін математикалық түрде шығару қиынға соғады. Осындай кезде координаталық әдіс арқылы шешеміз: . Бірақ та шешімді табу үшін математикалық түрде шығару қиынға соғады. Осындай кезде координаталық әдіс арқылы шешеміз:Берілген теңдеуді екі функцияға бөліп жазайық: 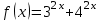 , , 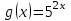 – көрсеткіштік функциялар. – көрсеткіштік функциялар.Екі графиктің қиылысуы нүктелерінің абсциссалары теңдеудің түбірі болатынын ұмытпайық. 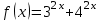 , , 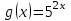 функцияларын координаталық жазықтыққа бейнелейміз (34-сурет). функцияларын координаталық жазықтыққа бейнелейміз (34-сурет).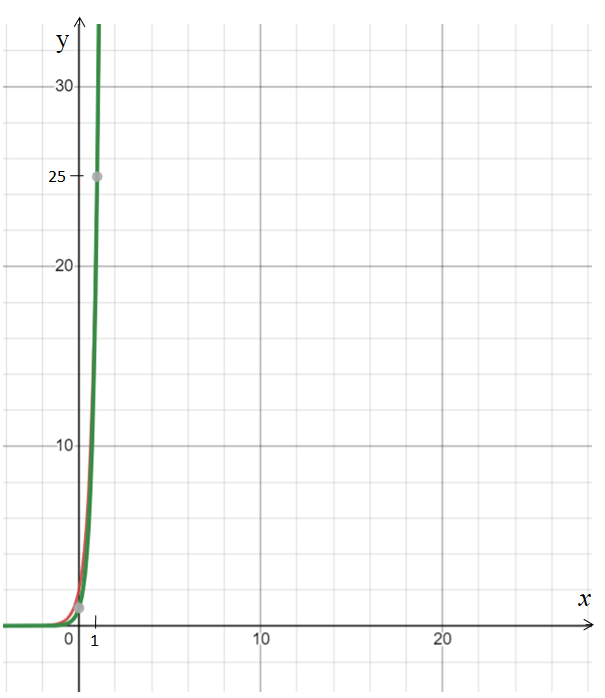 34-сурет. Екі график 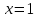 нүктесінде қиылысады. нүктесінде қиылысады.Жауабы: -1; 3.1.9 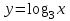 функциясын келесі координаталар бойынша график құрыңыз. функциясын келесі координаталар бойынша график құрыңыз.Шешуі: 8-кесте
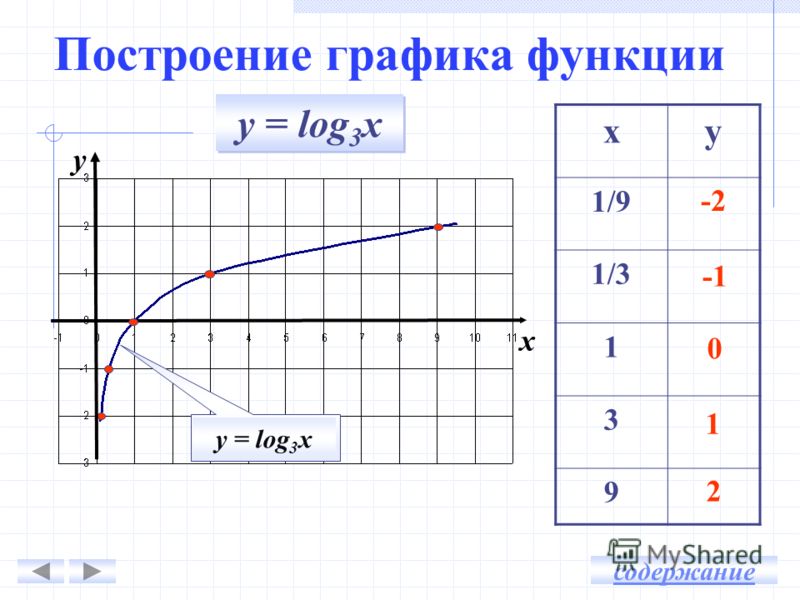 35-сурет |