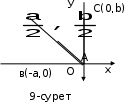уа. диплом2. Дипломды Жмыс таырыбы Функциялармен тедеулерді графиктерін трызуа координаттар дісін олдану
 Скачать 3.49 Mb. Скачать 3.49 Mb.
|
|
1.4 Мектеп оқулықтарын талдау Мектеп геометриясының курсы қаншалықты құрылса да, онда теоремаларды дәлелдеудің және есептерді шешудің әртүрлі әдістері бар екендігі белгілі. Мұндай әдістердің ішінде геометриялық түрлендіру әдісі, координаттар әдісі, векторлық әдіс сияқты әдістер маңызды орын алады. Бұл әдістердің өздері бір-бірімен тығыз байланысты. Орта мектепке арналған геометрия оқулықтарының авторлары ашқан тұжырымдамаға байланысты бұл немесе басқа әдіс басым болуы мүмкін. Сонымен, оқулықта [22] координаттар әдісі белсенді рөл атқарады, ол өте жемісті. Математика бойынша мектеп бағдарламасында координаттар әдісіне аз көңіл бөлінеді. Геометрия курсын зерттеудің мақсаттары бөлімінде: "теоремаларды дәлелдеу және есептерді шешу кезінде... геометриялық түрлендірулер, векторлар мен координаттар қолданылады"делінген. Сондықтан бағдарлама координаталар әдісін мәселелерді шешу әдісі ретінде зерттеуді мақсат етпейді. Бағдарламада "геометрия курсын оқу нәтижесінде студенттер қарапайым стандартты есептерді шешу үшін координаттарды қолдана білуі керек"делінген. Теоремаларды дәлелдеу және есептерді шешу үшін студенттердің координаттар әдісін игеруі туралы сөз айтылмайды. "Қарапайым стандартты міндеттерге" баса назар аударылады, ал координаталар әдісі стандартты емес және өте күрделі (егер сіз оларды басқа жолдармен шешпесеңіз) мәселелерді шешуде жақсы нәтиже көрсетеді. Орта мектеп үшін математика бағдарламасына сәйкес координаттар алғаш рет 5-сыныпта пайда болады. Сонымен қатар, балалар түзу сызықтағы сандардың бейнесімен және нүктелердің координаттарымен танысады. Сонымен қатар, бұл ұғымдарды оқулықтарға енгізу әртүрлі. Сонымен, оқулықта [3] бірінші тараудың бесінші абзацында координаталық сәуле қарастырылады, оның көмегімен болашақта натурал және бөлшек сандарды салыстыру, сонымен қатар натурал Сандарға қосу және азайту әрекеттерін суреттеу болады. Оқулық авторлары координаталық тікелей ұғыммен [4] 6-сыныптағы оқушыларды таныстырады. Оқулықта [6] "координаталық сәуле"анықтамасы жоқ. 5-сыныптың басында авторлар координаталық сызық ұғымын енгізеді, дегенмен 6-сыныпта болатын теріс сандарды зерттемес бұрын, жұмыс координаталық сәулені білдіретін координаталық түзудің оң бөлігімен ғана жүреді. Бұл өте ыңғайлы емес, өйткені осы координаталық сызықтың басқа бөлігі туралы әлі қажет емес сұрақтар туындауы мүмкін. Жалпы, оқулықтарда [3-4] координаталық сәулені (координаталық түзуді, содан кейін координаталық жазықтықты) анықтауға байланысты көбірек тапсырмалар бар және оқулықтарға қарағанда басқа ұғымдарды енгізу немесе сандар бойынша әрекеттерді қарастыру үшін жиі жүгінеді [6-7]. Бағдарламаға сәйкес геометрияда координаталар келесі көлемде зерттеледі: "Координаталық жазықтық. Берілген координаттары бар жазықтықтың екі нүктесі арасындағы қашықтық формуласы. Түзу мен шеңбердің теңдеуі"[24]. Сонымен, оқулықта [2] 9-сыныптағы жеке тарау координаттарға арналған. Сонымен қатар, бұл материал "векторлар" тақырыбын зерттегеннен кейін, бірақ векторлардың скаляр көбейтіндісін зерттегенге дейін зерттеледі. Тақырыпты қарауға 18 сағат беріледі. Бұл оқулықта координаттар әдісі жеке тарауға бөлінген, онда вектордың координаттары, шеңбер мен түзудің теңдеуі зерттеледі, координаттардағы қарапайым есептер шешіледі. Бұл тарауда алгебраның көмегімен геометриялық фигураларды зерттеу әдісі ретінде координаттар әдісі туралы түсінік берілген. Оқушылар координаталар жүйесін енгізу арқылы мәселелерді шешуді үйренеді. Автор оқушыларды координаталар әдісін тек теңдеу бойынша фигураларды құру үшін есептерге қолдануда ғана емес, сонымен қатар дәлелдеу есептерін шешуде де, геометриялық формулаларды шығаруда да білуге үйретуді мақсат етеді. Оқулықтағы геометрия бойынша басқа мектеп оқулықтарынан айырмашылығы [22] координаттар орталық орындардың бірін алды. Олар "Төртбұрыштар" және "Пифагор теоремалары"тақырыптарын зерттегеннен кейін 8-сыныптан бастап енгізіледі. Тақырыпты зерттеуге 19 сағат бөлінеді. Жазықтықтағы координаталарды, шеңбер мен түзудің теңдеулерін енгізумен байланысты негізгі ұғымдарды қарастырғаннан кейін бірден студенттер екі шеңбердің қиылысы, түзу мен шеңбердің қиылысы, 0° - дан 180° - қа дейінгі кез-келген бұрыштың синусын, косинусын және тангенсін анықтау сияқты сұрақтарды зерттейді. Бұл студенттер танысатын координаттар әдісінің алғашқы қосымшалары. Алгебра курсында  теңдеуіне негізделген, мұндағы теңдеуіне негізделген, мұндағы 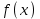 берілген функция осы теңдеумен анықталған қисық сызықты құрады, яғни берілген функция осы теңдеумен анықталған қисық сызықты құрады, яғни  функциясының графигін салды . Осылайша, олар "алгебрадан геометрияға"дейін жүрді. Геометриядағы координаталар әдісін зерттеген кезде біз кері жолды таңдаймыз: кейбір қисықтардың геометриялық қасиеттеріне сүйене отырып, олардың теңдеуін шығарамыз, яғни "геометриядан алгебраға"барамыз. 8-сыныпта оқулық бойынша [22] және 9-сыныпта оқулық бойынша [2] түзу мен шеңбердің теңдеуі қарастырылады. Бұл жағдайда "фигураның теңдеуі" деген жалпы ұғымға назар аударылады: "декарттық координаталардағы жазықтықтағы фигураның теңдеуі-бұл фигураның кез-келген нүктесінің координаттарымен қанағаттанатын екі белгісіз функциясының графигін салды . Осылайша, олар "алгебрадан геометрияға"дейін жүрді. Геометриядағы координаталар әдісін зерттеген кезде біз кері жолды таңдаймыз: кейбір қисықтардың геометриялық қасиеттеріне сүйене отырып, олардың теңдеуін шығарамыз, яғни "геометриядан алгебраға"барамыз. 8-сыныпта оқулық бойынша [22] және 9-сыныпта оқулық бойынша [2] түзу мен шеңбердің теңдеуі қарастырылады. Бұл жағдайда "фигураның теңдеуі" деген жалпы ұғымға назар аударылады: "декарттық координаталардағы жазықтықтағы фигураның теңдеуі-бұл фигураның кез-келген нүктесінің координаттарымен қанағаттанатын екі белгісіз 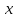 және және 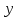 бар теңдеу. Және керісінше: берілген теңдеуді қанағаттандыратын кез келген екі cан фигураның белгілі бір нүктесінің координаталары болып табылады" [22]. Жазықтықтағы фигураның теңдеуін жалпы түрде былай жазуға болады: бар теңдеу. Және керісінше: берілген теңдеуді қанағаттандыратын кез келген екі cан фигураның белгілі бір нүктесінің координаталары болып табылады" [22]. Жазықтықтағы фигураның теңдеуін жалпы түрде былай жазуға болады: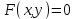 , мұндағы , мұндағы 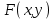 екі айнымалы функция екі айнымалы функция 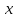 және және 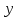 . .Оқулық [28] мектеп геометрия курсын құрудың авторлық тұжырымдамасын жүзеге асырады, дәстүрлі оқулықтармен салыстырғанда геометриялық есептерді шешу әдістеріне көбірек көңіл бөлінеді. Бұл оқулықтағы координаттар әдісі 9-сыныптың соңғы тақырыбы болып табылады. Оны зерттеу кезінде студенттер жазықтықтағы декарттық координаттармен танысады, "жазықтық сызықтардың: түзулер мен шеңберлердің" екі теңдеуін қарастырады, олар болашақта есептерді шешуде қажет болады. Бұл процесте координаталық әдіспен мәселелерді шешуге қажетті кейбір дағдылар жасалады. Оқулықта осы тақырып бойынша салыстырмалы түрде аз теориялық материал бар екенін атап өткен жөн. Мысалы, жалғыз дәлелденген формула (және тек бір жағдай үшін  және және 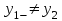 ), сызықтар теңдеулерін қоспағанда, нүктелер арасындағы қашықтық формуласы болып табылады. Оқулықтардан айырмашылығы [22] және [2] кесіндінің орта формуласы теориялық материалда қарастырылмайды, дегенмен практикалық тапсырмаларда " ), сызықтар теңдеулерін қоспағанда, нүктелер арасындағы қашықтық формуласы болып табылады. Оқулықтардан айырмашылығы [22] және [2] кесіндінің орта формуласы теориялық материалда қарастырылмайды, дегенмен практикалық тапсырмаларда "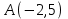 және және 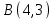 координаталық түзу нүктелерін қарастырыңыз. Егер координаталық түзу нүктелерін қарастырыңыз. Егер 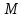 - - 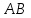 ортасы болса, ортасы болса, 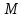 нүктесінің координаталарын табыңыз", осылайша білім алушыларға осы нақты жағдайды қарастырып, координаттар ұғымдары мен нүктелер арасындағы қашықтық формуласын қолдана отырып, сегменттің ортасының координаталық формуласын өздері шығаруға шақырылады. нүктесінің координаталарын табыңыз", осылайша білім алушыларға осы нақты жағдайды қарастырып, координаттар ұғымдары мен нүктелер арасындағы қашықтық формуласын қолдана отырып, сегменттің ортасының координаталық формуласын өздері шығаруға шақырылады.Автор білім алушыларға фигура ұғымын ұсынбайды, бірақ оқушыларға есептерді шешуде қажет болатын "жазық сызықтар" теңдеулерін егжей-тегжейлі қарастырады. Бұл шеңбер мен түзудің теңдеулері. Векторларды зерттегеннен кейін "координаталық әдіс" параграфы қарастырылады, онда екі бөлшектелген мәселенің мысалында Аполлонийдің шеңбері қарастырылады, ал екіншісінде координаттар жүйесін таңдауға назар аударылады, студенттерге осы әдіспен шешілетін бірқатар тапсырмалар ұсынылады. Бұл өте күрделі тапсырмалар, негізінен нүктелердің геометриялық орнын табуға байланысты. Бұл оқулықтың авторы "координаталық әдіс олардың ең әмбебап әдістерінің бірі" деп мойындайды, бірақ "барлық жағдайларға арналған әдіс жоқ"дейді. «Функция» тақырыбы мектептегі математика курсындағы орталық тақырыптардың бірі болып табылады. Бұл функционалдық сызықтың мектептегі алгебра курсына, алгебра курсына және қызыл жіппен талдаудың басталуына байланысты. Алгебра, алгебра және талдаудың бастаулары бойынша мектеп оқулықтары мен оқу құралдарын, ҰБТ материалдарын талдау тапсырмалардың басым бөлігі «Функция» тақырыбына арналғанын көрсетеді. Тапсырмаларда жыл сайын берілген аралықта функцияның ең үлкен және ең кіші мәндерін табу тапсырмалары болуы кездейсоқ емес. Тапсырмалардың мазмұны жыл сайын дерлік өзгермейтініне қарамастан, барлық түлектер бұл тапсырманы орындай бермейді. Мұның себептерінің бірі – осы пәнді оқуға бөлінген сағат санының жеткіліксіздігі (аптасына 3-5 сағат). Сонымен қатар математика мұғалімдерімен жүргізілген сауалнамалар мен әңгімелесулер әдістемелік әдебиеттерде берілген тақырып бойынша есептерді шығаруды оқыту әдістемесіне жеткіліксіз көңіл бөлінетінін көрсетеді. Бірінші бөлім бойынша қорытынды 1. Мектептегі координаттар әдісін зерттеудің негізгі ережелері және келесі мақсаттары бөліп көрсетілді: оқушыларға есептерді шешудің тиімді әдісін және бірқатар теоремалардың дәлелдерін беру; осы әдіс негізінде алгебра мен геометрияның тығыз байланысын көрсетіледі; оқушылардың есептеу және графикалық мәдениетін дамытуға ықпал ету. 2. Тікбұрышты координаттар біздің дәуірімізге дейін қолданылған. Александрия мектебінің ежелгі математигі Аполлоний Пергский (б. з. д. III-II ғасырда өмір сүрген) қазірдің өзінде тікбұрышты координаттарды қолданды. Ол сол кезде белгілі қисықтарды, параболаны, гиперболаны және эллипсті анықтап, зерттеді. 3. Есептерді алгебралық және геометриялық координаттар әдісімен шешу үшін 3 кезеңін белгіледік: 1. Тапсырманы координаттық (Талдамалық) тілге аудару; 2. Аналитикалық өрнекті түрлендіру; 3. кері аударма, яғни координаталық тілден тапсырма тұжырымдалған тілге аудару. Мысал ретінде келесі теңдеуін алдық. 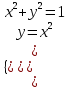 теңдеулер жүйесінің шешімі таптық. 4. Мектеп оқулықтарына талдау жүргізілді. Зерттеу жұмысының тақырыбы қай сыныптың математика оқулығының тақырыптарымен сәйкес екенін қарастырдық. Әр сыныптың оқулығының «Координаталық жазықтық» тақырыбына қанша сағат бөлінетіні зерттелді. 2 Функциялармен теңдеулердің графиктерін салу 2.1 Координаттық әдісті оқытатын есептер Координаталық әдісті қолдана білу қабілетін қалыптастыру әдістемесін жасау үшін есептерді шешудің логикалық құрылымы шешуші ойлауға қойылатын талаптарды анықтау қажет. Координаттық әдіс білім алушылардың осы әдісті практикада қолдануға ықпал ететін дағдыларының болуын қамтамасыз етеді. Бірнеше мәселенің шешімін талдайық. Осы талдау барысында біз есептерді шешуде координаталық әдісті қолдану қабілетінің құрамдас бөлігі болып табылатын дағдыларды бөліп аламыз. Бұ л шеберліктің компоненттерін білу оның элементтік қалыптасуын жүзеге асыруға мүмкіндік береді. №1 тапсырма: 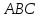 үшбұрышында үшбұрышында  , , 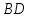 =медиана. =медиана.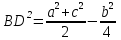 екенін дәлелдеңіз. екенін дәлелдеңіз.Координаталар жүйесін 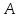 нүктесі координаталардың басы, ал нүктесі координаталардың басы, ал 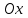 осі түзу осі түзу 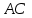 болатындай етіп таңдаймыз (2-сурет) (координаталар жүйесін оңтайлы таңдау мүмкіндігі, яғни.осы нүктелердің координаттарын табу оңай). Таңдалған координаттар жүйесінде болатындай етіп таңдаймыз (2-сурет) (координаталар жүйесін оңтайлы таңдау мүмкіндігі, яғни.осы нүктелердің координаттарын табу оңай). Таңдалған координаттар жүйесінде 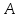 , , 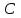 және және 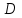 нүктелерінің мынадай координаттары болады: нүктелерінің мынадай координаттары болады: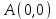 , , 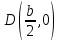 және және 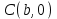 (берілген нүктелердің координаталарын есептеу білігі). (берілген нүктелердің координаталарын есептеу білігі).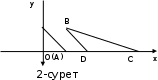 Содан кейін формуланы қолдана отырып, оның координаттарымен берілген екі нүктенің арасындағы қашықтықты табыңыз (координаталармен берілген екі нүктенің арасындағы қашықтықты таба білу): 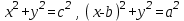 (1) (1)Сол формула бойынша 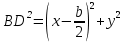 (2). (1) формулаларын қолдана отырып, біз (2). (1) формулаларын қолдана отырып, біз 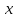 және және 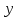 табамыз. Олар: табамыз. Олар: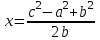 , , 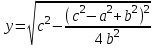 Әрі қарай, 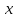 және және 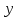 формуласын (2) алмастыра отырып, табамыз (алгебралық өрнектерді түрлендіруді орындай білу) формуласын (2) алмастыра отырып, табамыз (алгебралық өрнектерді түрлендіруді орындай білу): 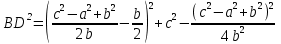 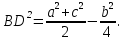 №2 тапсырма: Осы екі нүктеден қашықтықтың квадраттарының айырмашылығы тұрақты болатын нүктелер жиынтығын табыңыз. Біз координаталар жүйесін таңдаймыз, сондықтан 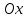 осі осі 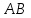 сызығымен сәйкес келеді, ал сызығымен сәйкес келеді, ал 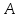 нүктесі координаталардың басы болады (координаттар жүйесін оңтайлы таңдау мүмкіндігі). нүктесі координаталардың басы болады (координаттар жүйесін оңтайлы таңдау мүмкіндігі).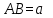 делік, содан кейін таңдалған координаттар жүйесінде делік, содан кейін таңдалған координаттар жүйесінде 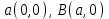 . .(берілген нүктелердің координаттарын таба білу) М(х,у) нүктесі 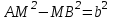 болған кезде ғана қажетті жиынтыққа жатады, мұндағы болған кезде ғана қажетті жиынтыққа жатады, мұндағы 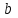 – тұрақты шама (геометриялық тілді аналитикалық тілге аудара білу, фигуралардың теңдеулерін құру). – тұрақты шама (геометриялық тілді аналитикалық тілге аудара білу, фигуралардың теңдеулерін құру).Екі нүкте арасындағы қашықтық формуласын қолдана отырып, біз аламыз (координаттармен берілген нүктелер арасындағы қашықтықты есептеу білігі): 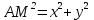 , ,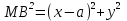 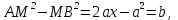 немесе 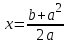 . Бұл теңдеу . Бұл теңдеу 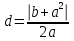  осіне параллель және осіне параллель және 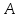 нүктесінен қашықтыққа дейінгі түзудің теңдеуі болып табылады (теңдеудің артында нақты геометриялық бейнені көре білу). нүктесінен қашықтыққа дейінгі түзудің теңдеуі болып табылады (теңдеудің артында нақты геометриялық бейнені көре білу).Бұл мәселені шешу үшін жоғарыда аталған дағдыларды игеру қажет екенін көру қиын емес. Сонымен қатар, берілген есепті, сондай-ақ басқа есептерді шешу үшін белгілі бір фигуралардың теңдеулерін құру қабілетіне қарама-қарсы болатын белгілі бір геометриялық кескінді "теңдеудің артында көру" мүмкіндігі маңызды. 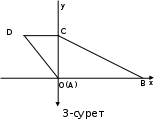 Белгіленген дағдылар күрделі мәселелерді шешуге негіз болып табылады. №3 тапсырма: Трапецияда кіші диагональ негіздерге перпендикуляр болады. Егер қарама-қарсы бұрыштардың қосындысы  тең болса және негіздер тең болса және негіздер 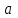 және және 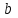 болса, үлкен диагональды табыңыз. болса, үлкен диагональды табыңыз.Координаталардың осьтерін кіші диагональ бойынша және негіздердің біріне бағыттаңыз (3-сурет), (координаттар жүйесін оңтайлы таңдау мүмкіндігі). Содан кейін 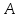 нүктесінің координаттары болады нүктесінің координаттары болады 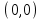 , , 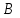 нүктесі – нүктесі – 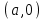 , , 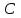 нүктесі – нүктесі – 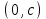 , , 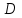 нүктесі – нүктесі – 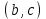 (берілген нүктелердің координаттарын таба білу). (берілген нүктелердің координаттарын таба білу).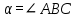 және және 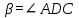  трапециясындағы өткір бұрыштар болса да, олардың қосындысы трапециясындағы өткір бұрыштар болса да, олардың қосындысы  . тең . Үлкен . тең . Үлкен 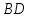 диагоналінің ұзындығын есептеу үшін диагоналінің ұзындығын есептеу үшін 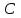 мәнін табу керек, оны 2 жолмен есептеуге болады. Бірінші мәнін табу керек, оны 2 жолмен есептеуге болады. Бірінші 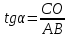 формула бойынша формула бойынша 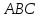 дұрыс үшбұрышынан дұрыс үшбұрышынан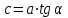 табамыз. табамыз. 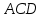 үшбұрышының екінші әдісі: үшбұрышының екінші әдісі: 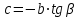 . Осы жерден шықты . Осы жерден шықты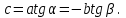 (1) (1)Теңдіктен (1) қатынасты табамыз 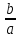 : ол - : ол -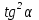 тең өйткені тең өйткені 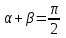 . . 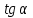 қысқартамыз. Ол қысқартамыз. Ол 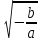 тең, осыған сүйене отырып, тәуелділікті (1) қолдана отырып аламыз тең, осыған сүйене отырып, тәуелділікті (1) қолдана отырып аламыз 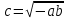 (жетіспейтін координаттарды белгілі шамалар арқылы білдіру мүмкіндігі). (жетіспейтін координаттарды белгілі шамалар арқылы білдіру мүмкіндігі).Әрі қарай, екі нүкте арасындағы қашықтықтың координаталық формуласын пайдаланып, 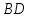 ұзындығын табамыз (координаттармен берілген нүктелер арасындағы қашықтықты есептеу білігі). Ол ұзындығын табамыз (координаттармен берілген нүктелер арасындағы қашықтықты есептеу білігі). Ол 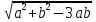 тең. тең.Сонымен, нақты жағдайларда координаталық әдісті қолдану қабілетінің компоненттері келесі дағдылар болып табылады: – геометриялық тілді есептердің бір түрі үшін аналитикалық тілге, ал екіншісі үшін аналитикалық тілді геометриялық тілге аудару; – берілген координаттар бойынша нүкте қою; – берілген нүктелердің координаттарын табу; – координаталармен берілген нүктелер арасындағы қашықтықты есептеңіз; – координаттар жүйесін таңдау оңтайлы; – берілген фигуралардың теңдеулерін құру; – теңдеудің артында нақты геометриялық кескінді көру; – алгебралық қатынасты түрлендіруді орындау. Бұл дағдыларды координаталық әдісті құрайтын келесі тапсырмалардың мысалында пысықтауға болады: – нүктені оның координаттары бойынша құру міндеттері; – берілген нүктелердің координаталарын табу міндеттері; – координаттармен берілген нүктелер арасындағы қашықтықты есептеуге арналған тапсырмалар; – координаттар жүйесін оңтайлы таңдау міндеттері; – фигура теңдеуін оның сипаттамалық қасиеті бойынша құруға арналған есептер; – фигураны оның теңдеуі бойынша анықтауға арналған міндеттер; – алгебралық теңдіктерді түрлендіруге арналған есептер. Біз осындай тапсырмалардың мысалдарын келтіреміз. I. Жазықтықтағы нүктелердің құрылысы. Оқушылар математикалық материалды оқу кезінде координаталық түзумен, содан кейін координаталық жазықтықпен 5-6 сыныптарда танысады. Сонымен қатар, динамикада қажетті материалды ұсынуға, иллюстрациялар мен дыбыстық эффектілердің барлық түрлерін қолдануға мүмкіндік беретін мультимедиялық презентацияларды қолдану ыңғайлы, осылайша студенттерді қызықтырады және жақсы көрнекі құрал бола алады. Бір мысал-оқулыққа негізделген "координаттар әдісі" презентациясы [7]. Координаталық жазықтықты зерттеуде қолдануға болатын бірнеше мысалдар келтірілген. Бұл тапсырмаларды қолдануға болады: барлық кластағы координаттары бойынша нүктелерді құру дағдыларын шыңдау үшін; артта қалған оқушыларға қосымша тапсырмалар үшін; зерттелетін тақырыпқа қызығушылықты дамыту үшін. 1) координаталық жазықтықта 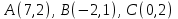 нүктелерін құрыңыз. нүктелерін құрыңыз.2) жазықтықта бірнеше нүктені белгілеңіз. Еркін координаттар жүйесін сызыңыз және ондағы берілген нүктелердің координаттарын табыңыз. 3) фигураларды олардың түйіндік нүктелерінің координаталары бойынша құрыңыз. Нұсқау: түйін фигураларды құрайтын сегменттердің ұштары ретінде қызмет ететін нүктелер деп аталады. Координаттары қатарынан үтір арқылы жазылған нүктелерді бір-бірімен қатар жалғаңыз. Егер координаталар " " белгісімен бөлінсе, онда тиісті нүктелерді қосуға болмайды. Олар көмекші элементтерді бейнелеу үшін қажет. Камбала (4-сурет): 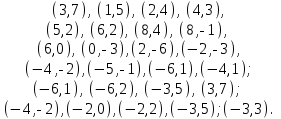 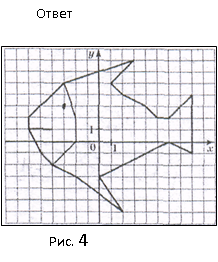 4-сурет Б) ең қалың нүктеден сағат тілімен қозғалу арқылы суретте көрсетілген нүктелердің координаттарын табыңыз (5а, 5ә-сурет)? 2.1.1 4-суретте көрсетілген нүктелердің координаттарын табыңыз: 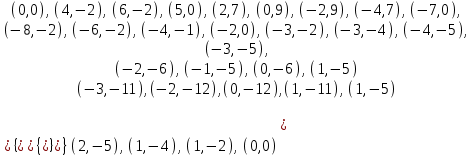  2.1.2 4-суретте көрсетілген нүктелердің координаттарын табыңыз: 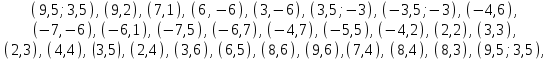 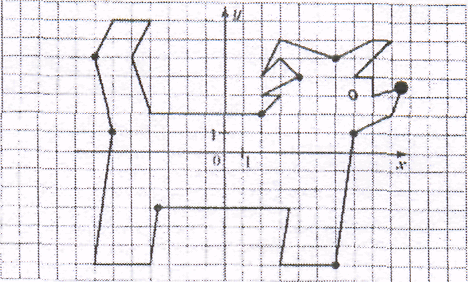 5ә-сурет 2.1.3 Қоян (6а-сурет): 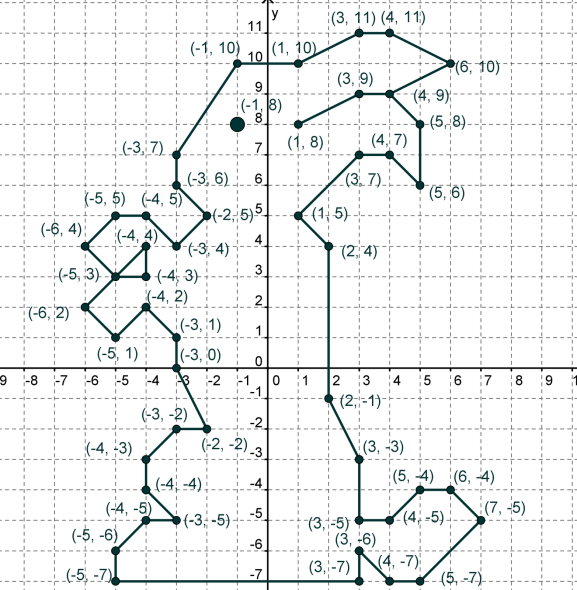 6а-сурет Өзіндік жұмыс ретінде келесі суреттерді беруге болады: 2.1.4 (6ә-сурет): 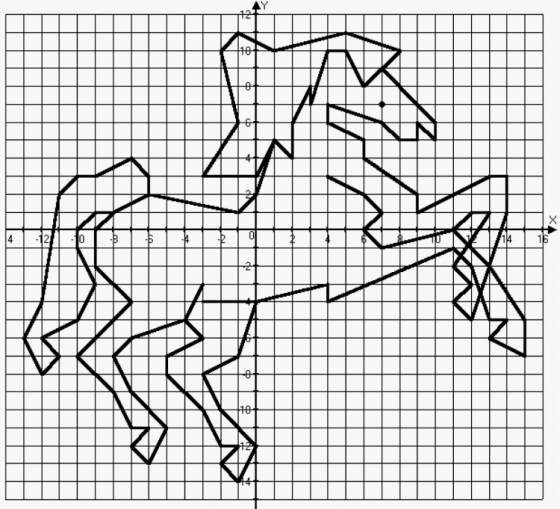 6ә-сурет 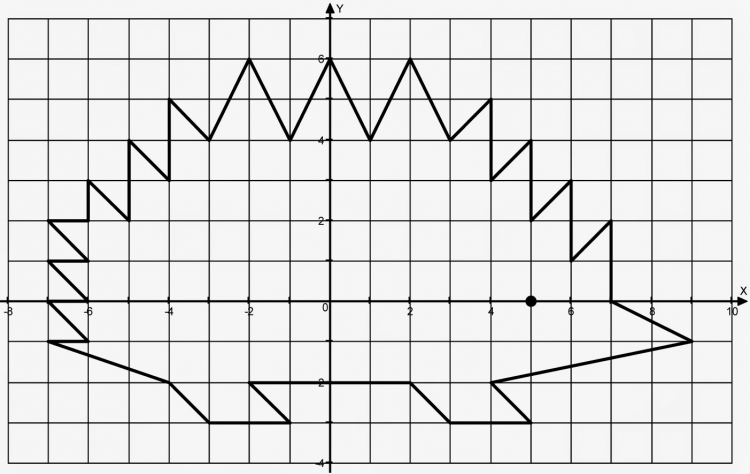 6б-сурет 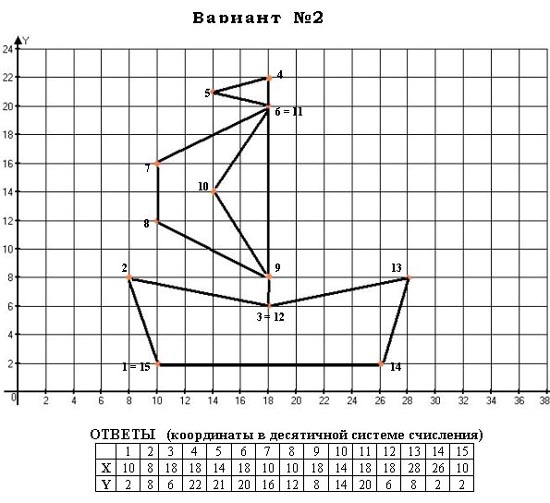 6в-сурет II.Координаттар жүйесін таңдау міндеттері Координаттар жүйесін таңдау координаттар әдісін қолдану кезінде өте маңызды. Мысалы, оқулықта қарастырылған мәселені алайық [2] "дұрыс үшбұрыштың гипотенузасының ортасы оның шыңдарынан тең". Координаттар әдісін қолданудағы алғашқы қадам – алгебралық есептеулер қарапайым болатын осьтер мен координаттар жүйесін таңдау. Бұл тапсырма үшін координаттар жүйесін сәтті таңдау 7-суретте көрсетілген. Осылайша, координаталардың басы  нүктесіне қойылады, ал осьтер нүктесіне қойылады, ал осьтер 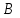 және және 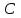 нүктелері арқылы тартылады, осылайша бұл нүктелер осьтердің оң сәулелерінде орналасады. Демек, нүктелері арқылы тартылады, осылайша бұл нүктелер осьтердің оң сәулелерінде орналасады. Демек, 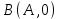 және және 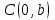 . Сондықтан кесіндінің орта формуласы бойынша . Сондықтан кесіндінің орта формуласы бойынша 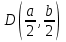 . Енді . Енді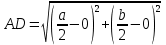 , , 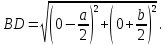 Сондықтан  . . 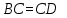 сегментінің ортасын анықтау арқылы теорема дәлелденді. сегментінің ортасын анықтау арқылы теорема дәлелденді. 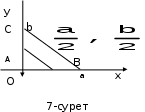 Координаттар жүйесін басқаша таңдауға болады (8, 9-суреттер). Егер сіз осьтерді кездейсоқ таңдасаңыз, онда оңай тапсырманы өте қиын тапсырмаға айналдыруға болады. Бастау үшін дәлелдеу 10-суретке сүйене отырып, 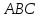 үшбұрышының үшбұрышының 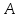 шыңында дұрыс бұрышы бар екенін алгебралық түрде білдіруге мүмкіндік беретін әдісті табу керек. Сіз мұны жасай аласыз, бірақ бұл оңай болмайды. шыңында дұрыс бұрышы бар екенін алгебралық түрде білдіруге мүмкіндік беретін әдісті табу керек. Сіз мұны жасай аласыз, бірақ бұл оңай болмайды.
Сондықтан, 6-сыныптан бастап оқушыларына координаталар жүйесін ерікті түрде таңдау мүмкіндігі туралы идеяларды дамыту қажет. Бұл жұмысты проблемаларды шешу процесінде жүргізген жөн. Пропедевтикалық жұмыс үшін оқулықтан 6-сыныпта нүктелердің координаталарын сызбаға сәйкес табуға, оларды осьтердің бағытын және шығу тегін өзгерту арқылы әртараптандыруға болады. АВ кесіндісінің ұзындығы – 5 см. а) кесіндінің ұштарының координаттарын оңай анықтауға болатын координаттар жүйесін таңдаңыз. ә) кесіндінің ұштарының координаталары 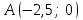 , , 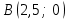 болатындай координаталар жүйесін таңдаңыз. болатындай координаталар жүйесін таңдаңыз.2 см жағы бар  квадратын жасаңыз; квадратын жасаңыз; 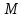 нүктесін белгілеңіз - шаршының ортасы. Координаталардың басын нүктесін белгілеңіз - шаршының ортасы. Координаталардың басын 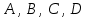 нүктелеріне кезекпен орналастырыңыз және координаталар осьтерінің бағытын таңдаңыз, сондықтан әр координаттар жүйесіндегі нүктелеріне кезекпен орналастырыңыз және координаталар осьтерінің бағытын таңдаңыз, сондықтан әр координаттар жүйесіндегі 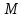 нүктесі координаттарға ие болады нүктесі координаттарға ие болады 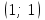 . Бірлік үшін ұзындығы 1 см кесінді алыңыз. . Бірлік үшін ұзындығы 1 см кесінді алыңыз.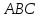 үшбұрышы тең жақты (жағының ұзындығы – 6 см.). Координаталар жүйесін оның шыңдарының координаттарын анықтау оңай болатындай етіп таңдаңыз. үшбұрышы тең жақты (жағының ұзындығы – 6 см.). Координаталар жүйесін оның шыңдарының координаттарын анықтау оңай болатындай етіп таңдаңыз.III. Нүктелер арасындағы қашықтық 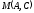 нүктесі координаталардың басынан және нүктесі координаталардың басынан және 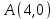 нүктесінен тиісінше 3 және 4 см қашықтықта орналасқан. нүктесінен тиісінше 3 және 4 см қашықтықта орналасқан.  тіктөртбұрышы берілген ( тіктөртбұрышы берілген (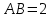 см, см, 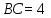 см.). Координаталар жүйесін оның шыңдарының см.). Координаталар жүйесін оның шыңдарының 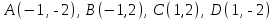 координаттары болатындай етіп қалай таңдауға болады? координаттары болатындай етіп қалай таңдауға болады? 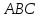 үшбұрышының жақтарының ұзындығы 3, 4 және 5 см координаталар жүйесін таңдап, ондағы үшбұрышының жақтарының ұзындығы 3, 4 және 5 см координаталар жүйесін таңдап, ондағы 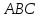 үшбұрышының шыңдарының координаталарын анықтаңыз. үшбұрышының шыңдарының координаталарын анықтаңыз.  төртбұрышының шыңдары мынадай координаттарға ие: төртбұрышының шыңдары мынадай координаттарға ие: 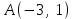 , , 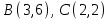 және және 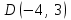 . Төртбұрыштың көрінісін орнатыңыз. . Төртбұрыштың көрінісін орнатыңыз. IV. Фигуралардың теңдеуін құру Бұл дағды координаталық әдісті есептерді шешуге қолдану кезінде қажет негізгі дағдылардың бірі болып табылады. 1. координаталар жүйесін сызыңыз. 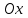 осінде осінде 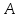 және және 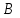 нүктелерін белгілеңіз, мыналарға жататын нүктелердің координаталары қанағаттандырылатын қатынастарды жазыңыз: А) нүктелерін белгілеңіз, мыналарға жататын нүктелердің координаталары қанағаттандырылатын қатынастарды жазыңыз: А) 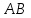 кесіндісі; ә) кесіндісі; ә) 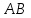 сәулесі; б) сәулесі; б) 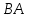 сәулесі; сәулесі; 2. шығу тегі мен 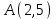 нүктесі бар түзудің теңдеуін жазыңыз. нүктесі бар түзудің теңдеуін жазыңыз.3. 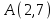 және және  нүктелері бар түзудің теңдеуін жазыңыз. нүктелері бар түзудің теңдеуін жазыңыз. 4. координаталық жазықтықта еркін түзу сызыңыз және оның теңдеуін табыңыз. 5. 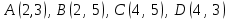 шыңдары бар тіктөртбұрыш нүктелерінің координаталарын қанағаттандыратын қатынастарды жазыңыз. шыңдары бар тіктөртбұрыш нүктелерінің координаталарын қанағаттандыратын қатынастарды жазыңыз.6. Координаталары теңсіздіктерді қанағаттандыратын жазықтық нүктелерінің жиындары қандай: а) 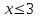 ; ә) ; ә) 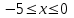 ; б) ; б)  ; в) ; в) 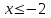 ; г) ; г) 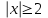 ; д) ; д)  ? ?7. Координаталары  және және 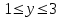 теңсіздіктер жүйесін қанағаттандыратын нүктелер жиыны қандай пішінді құрайды? теңсіздіктер жүйесін қанағаттандыратын нүктелер жиыны қандай пішінді құрайды?8. 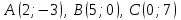 нүктелеріне симметриялы нүктелерді салыңдар: а) нүктелеріне симметриялы нүктелерді салыңдар: а) 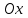 осіне; б) осіне; б)  осі; в) I және III координаталық бұрыштардың биссектрисалары. Мына координаталарды жаз. осі; в) I және III координаталық бұрыштардың биссектрисалары. Мына координаталарды жаз.9. 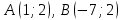 нүктелері координаталық осьтердің қайсысына симметриялы екенін анықтаңыз. нүктелері координаталық осьтердің қайсысына симметриялы екенін анықтаңыз.10. 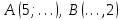 нүктелері нүктелері 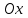 осіне қатысты симметриялы. Жетіспейтін координаталарды жазыңыз. осіне қатысты симметриялы. Жетіспейтін координаталарды жазыңыз.11. 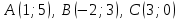 нүктелерінің кескіндерін параллель тасымалдау а) нүктелерінің кескіндерін параллель тасымалдау а)  тұрғызу; ә) тұрғызу; ә) 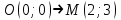 . Олардың координаталарын жазыңдар. . Олардың координаталарын жазыңдар.12. 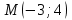 нүктесін нүктесін 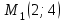 нүктесіне салыстыру үшін қандай параллель аударманы қолдануға болады? нүктесіне салыстыру үшін қандай параллель аударманы қолдануға болады?13. 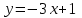 және және  түзулерінен түзулерінен 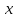 осіне қатысты симметриялы нүктелерді табыңыз. осіне қатысты симметриялы нүктелерді табыңыз.14. 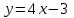 түзу координаталары түзу координаталары 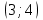 вектормен бейнеленетін түзудің теңдеуін жазыңыз. вектормен бейнеленетін түзудің теңдеуін жазыңыз.15. 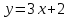 және және 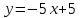 түзулерінде бір-бірінен 5 см қашықтықта орналасқан және түзулерінде бір-бірінен 5 см қашықтықта орналасқан және 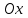 осіне параллель түзу сызыққа жататын нүктелерді табыңыз. осіне параллель түзу сызыққа жататын нүктелерді табыңыз. | ||||