Дипломная работа с элементами исследования. Дипломная работа Разработка и исследование алгоритмов обнаружения сигналов с эллипсными несущими
 Скачать 1.79 Mb. Скачать 1.79 Mb.
|
Использование оптимального алгоритма обнаружения радиоимпульсов с эллипсными несущими и полностью известными параметрами при воздействии прицельной помехи, используя корреляционный прием.В разделе спектральных характеристик эллипсных функций был показан их спектр. Откуда можно заключить, что добиться широкополосности радиосигналов можно путем использования в качестве несущего колебания периодическое селиусоидальное. Спектр непрерывного селиусоидального колебания с параметром формы 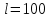 представлен на рис.5.1. Спектр периодической последовательности радиоимпульсов с селиусодальным несущим колебанием при таком же параметре формы представлен на рис.5.2. Частота несущего колебания была взята равной 100 МГц. представлен на рис.5.1. Спектр периодической последовательности радиоимпульсов с селиусодальным несущим колебанием при таком же параметре формы представлен на рис.5.2. Частота несущего колебания была взята равной 100 МГц. 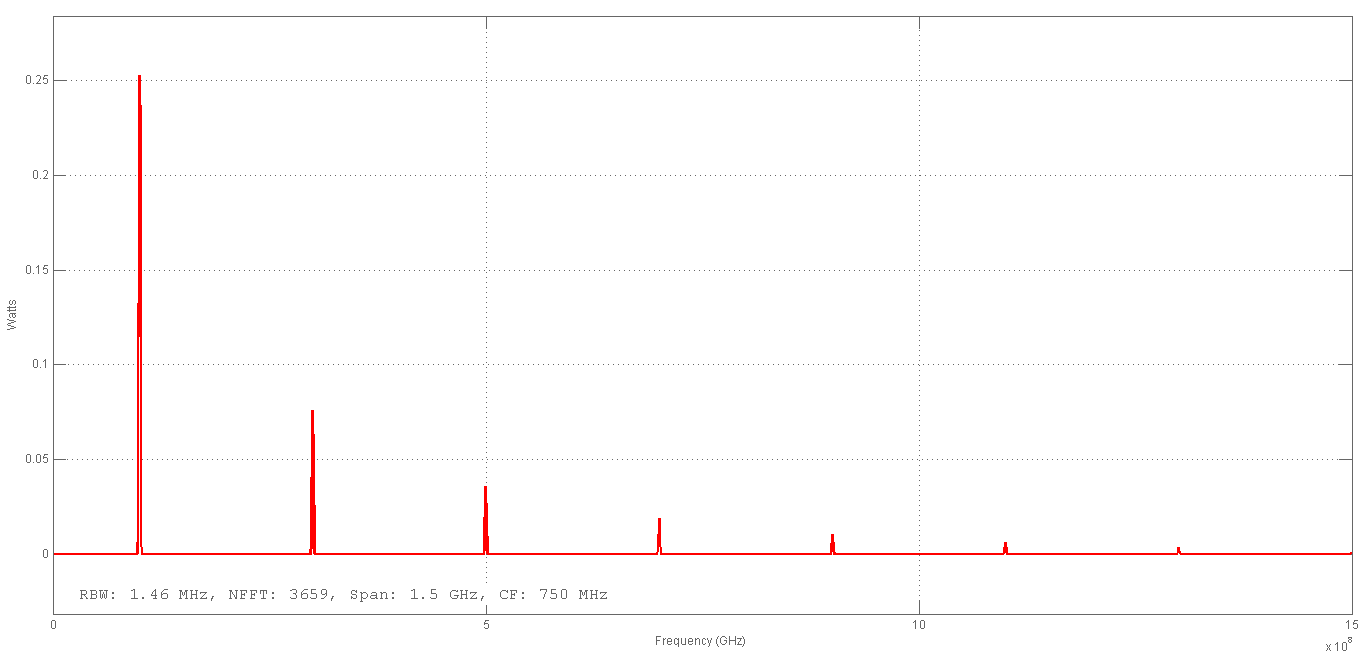 рис.5.1 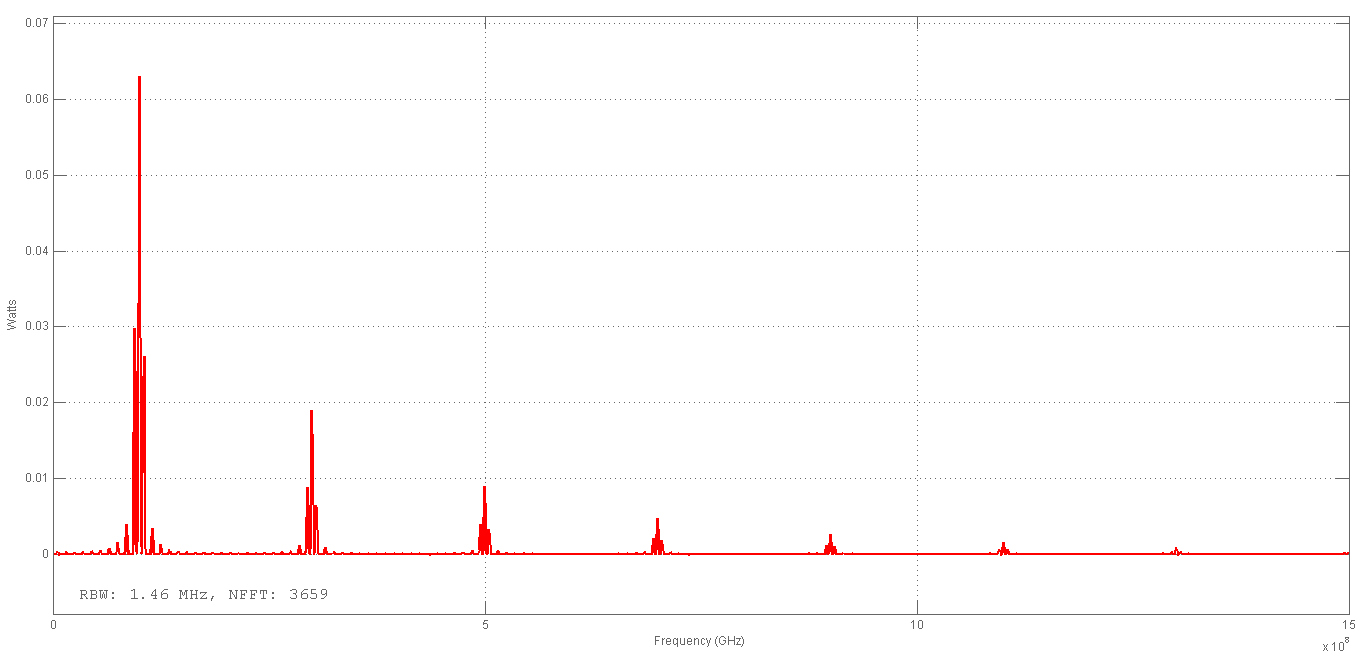 рис.5.2 Эффективная ширина спектра составила 20 ГГц. Откуда заключаем, что селиусоидальные сигналы относятся к широкополосным сигналам. При передаче информации на большие расстояния в некоторых случаях мощность преднамеренной помехи на входе приемника в его полосе пропускания может значительно превышать мощность сигнала. Одной из разновидностей данных помех является прицельная помеха (ПП). ПП представляет помеху, которая имеет равномерную спектральную плотность мощности 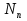 в полосе спектра сигнала, а вне полосы ее спектральная плотность мощности равна нулю. Для борьбы с прицельными помехами можно использовать широкополосные сигналы (ШПС). Помимо хорошо известных способов создания широкополосных сигналов, таких как ШПС модулированные псевдослучайной числовой последовательностью, ШПС на основе псевдослучайной перестройки радиочастоты, рассматривается возможность использования в качестве ШПС селиусоидальные сигналы. в полосе спектра сигнала, а вне полосы ее спектральная плотность мощности равна нулю. Для борьбы с прицельными помехами можно использовать широкополосные сигналы (ШПС). Помимо хорошо известных способов создания широкополосных сигналов, таких как ШПС модулированные псевдослучайной числовой последовательностью, ШПС на основе псевдослучайной перестройки радиочастоты, рассматривается возможность использования в качестве ШПС селиусоидальные сигналы.Помехоустойчивость приемника с согласованным фильтром (коррелятором) полностью определяется отношением сигнал-помеха на выходе фильтра 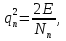 (10.2) (10.2)где 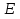 – энергия сигнала; – энергия сигнала; 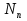 - спектральная плотность мощности помехи на входе приемника. Если помеха представляет собой только АБГШ, то максимальное отношение сигнала к белому шуму на выходе оптимального приемника не зависит от формы сигнала. Следовательно, если выделение сигнала происходит на фоне только внутренних шумов приемника, то помехоустойчивость приемников, согласованных с сигналами любой формы, будет одинаковой. Если же помеха является прицельной, то ее средняя мощность - спектральная плотность мощности помехи на входе приемника. Если помеха представляет собой только АБГШ, то максимальное отношение сигнала к белому шуму на выходе оптимального приемника не зависит от формы сигнала. Следовательно, если выделение сигнала происходит на фоне только внутренних шумов приемника, то помехоустойчивость приемников, согласованных с сигналами любой формы, будет одинаковой. Если же помеха является прицельной, то ее средняя мощность 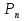 ограничена и она действует в полосе частот сигнала, поэтому ограничена и она действует в полосе частот сигнала, поэтому 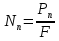 . Поскольку энергия сигнала . Поскольку энергия сигнала 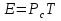 , то , то 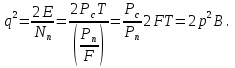 (*) (*)где отношение мощностей сигнала и помехи на входе приемника 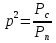 , а , а 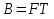 называется базой сигнала. Таким образом, при заданном отношении мощностей сигнала и шума помехоустойчивость тем выше, чем больше база принимаемых сигналов. Аналогичный вывод можно получить другим способом. Отношение сигнал-шум на входе СФ (коррелятора) в случае, когда на вход приходит сигнал, с которым фильтр согласован называется базой сигнала. Таким образом, при заданном отношении мощностей сигнала и шума помехоустойчивость тем выше, чем больше база принимаемых сигналов. Аналогичный вывод можно получить другим способом. Отношение сигнал-шум на входе СФ (коррелятора) в случае, когда на вход приходит сигнал, с которым фильтр согласован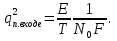 Отношением сигнал-помеха на выходе фильтра 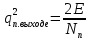 Выигрыш на выходе согласованного фильтра 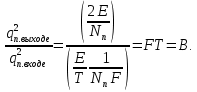 Получается, что улучшение отношения сигнал/шум на выходе фильтра по отношению к сигнал-шум на входе фильтра равняется базе сигнала. [11]. Формула (*) будет справедлива и при действии узкополосной помехи мощностью 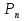 . Так, если представить оптимальный приемник в виде коррелятора, то на выходе перемножителя коррелятора произойдет расширение спектра этой помехи до значения полосы сигнала . Так, если представить оптимальный приемник в виде коррелятора, то на выходе перемножителя коррелятора произойдет расширение спектра этой помехи до значения полосы сигнала 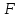 , а через интегратор с пределом интегрирования , а через интегратор с пределом интегрирования  пройдет лишь часть спектра помехи. В результате мощности помехи и сигнала на выходе коррелятора соответственно будут равны пройдет лишь часть спектра помехи. В результате мощности помехи и сигнала на выходе коррелятора соответственно будут равны 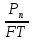 и и 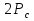 , а отношение сигнал-помеха определится из (*). , а отношение сигнал-помеха определится из (*).Соотношение (10.2) является основополагающим в технике борьбы с мощными помехами. Оно показывает, что при большой базе можно получить достаточное отношение сигнал-помеха 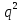 для надежного приема, даже если мощность сигнала на входе приемника много меньше мощности помехи, т.е. если для надежного приема, даже если мощность сигнала на входе приемника много меньше мощности помехи, т.е. если 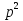 <<1. Действительно, пусть, например, <<1. Действительно, пусть, например, 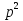 дБ=-40 дБ, а требуется иметь на выходе дБ=-40 дБ, а требуется иметь на выходе 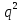 =13 дБ. В этом случае необходимо применять ШПС с базой Вдб=50 или =13 дБ. В этом случае необходимо применять ШПС с базой Вдб=50 или 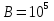 . База селиусоидального сигнала с параметром формы . База селиусоидального сигнала с параметром формы 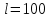 с длительностью с длительностью 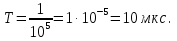 и эффективной шириной спектра и эффективной шириной спектра  равна: равна: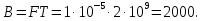 В случае использования синусоидального сигнала той же длительности при амплитудной модуляции речевым сигналом, база сигнала была бы равна  При этом выигрыш даже немодулированного селиусоидального сигнала составляет При этом выигрыш даже немодулированного селиусоидального сигнала составляет  , что почти достигает тридцати тысяч раз. , что почти достигает тридцати тысяч раз.Соотношение (10.2) указывает метод борьбы с мощными прицельными помехами: использование ШПС с большими базами, такими как радиосигналы с селиусоидальными несущими колебаниями. Этот метод непосредственно следует из теоремы Шеннона о пропускной способности канала связи с шумами. Эта теорема гласит, что можно найти такие коды, что пропускная способность канала связи 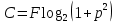 , (10.3) , (10.3)где 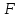 – ширина спектра сигналов, равная ширине полосы канала, – ширина спектра сигналов, равная ширине полосы канала, 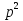 – отношение сигнал-помеха по мощности на входе приемника (10.3). Если действует мощная помеха, т.е. – отношение сигнал-помеха по мощности на входе приемника (10.3). Если действует мощная помеха, т.е. 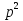 <<1, то <<1, то 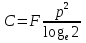 . Соответственно . Соответственно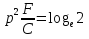 . (10.4) . (10.4)Согласно теореме Шеннона, если имеют место соотношения (10.3), (10.4), то можно нести передачу информации по такому каналу со сколь угодно малой вероятностью ошибки. В свою очередь, если в (10.2) заменить  на на 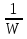 , где , где 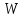 – скорость передачи информации (длительность двоичной единицы), то – скорость передачи информации (длительность двоичной единицы), то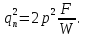 (10.5) (10.5)Сравнивая (10.5) с (10.4), можно заметить, что если положить 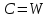 , т.е. вести передачу информации со скоростью, равной пропускной способности канала, то значение отношения сигнал-помеха , т.е. вести передачу информации со скоростью, равной пропускной способности канала, то значение отношения сигнал-помеха 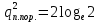 является пороговым для такой системы связи: если является пороговым для такой системы связи: если 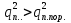 , то ошибка будет сколь угодно малой, если , то ошибка будет сколь угодно малой, если 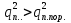 , то ошибка возрастет в соответствии с теоремой Шеннона. , то ошибка возрастет в соответствии с теоремой Шеннона.Таким образом, соотношение (10.2) и целесообразность применения ШПС для борьбы с мощными помехами вытекают из теоремы Шеннона. Впервые формула (10.2) была получена для шумовых помех с ограниченной средней мощностью, но она справедлива и для других помех, в том числе для узкополосных, импульсных и структурных (помехи, имеющие ту же структуру, что и полезный сигнал). [ 2, с. 184-189]. Выводы:
Проведенные аналитические рассуждения показали более высокую помехоустойчивость селиусоидальных колебаний по сравнению с синусоидальным колебанием. Полученные теоретические результаты, необходимо проверить, проведя серию экспериментов на имитационно-моделирующем комплексе. |
