Дипломная работа с элементами исследования. Дипломная работа Разработка и исследование алгоритмов обнаружения сигналов с эллипсными несущими
 Скачать 1.79 Mb. Скачать 1.79 Mb.
|
Использование оптимального алгоритма обнаружения радиоимпульсов с эллипсными несущими и полностью известными параметрами в аддитивном белом гауссовском шуме (АДБГ) при корреляционном приеме.
Теория оптимального радиоприема позволяет определить наилучшие виды передаваемых сигналов. Для этого следует сравнить значения потенциальной помехоустойчивости при различных видах сигналов. Сигнал, для которого при заданных условиях радиоприема получается наибольшая потенциальная помехоустойчивость, является наилучшим. Следует заметить, что теория оптимального радиоприема не оговаривает форму сигнала, поэтому будет считаться, данная теория применима и к селиусу. Условия, при которых рассматриваться задача оптимального обнаружения. Пусть на конечном фиксированном временном интервале [0, T] принимается колебание ξ(t), являющееся детерминированной функцией от полезного селиусоидального сигнала sel(t, λ) и помехи n(t): ξ(t)=F(sel(t,λ), n(t)), 0≤t≤T. (1) Здесь вектором λ={λ1, …, λm} обозначены параметры, от которых зависит сигнал. В нашем случае сигнал описывается селем, являющимся функцией эллипсной тригонометрии. Будем рассматривать радиоимпульс длительностью τи, который полностью укладывается в на интервале [0, T]. В этом случае : 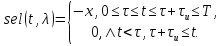 В данном случае сигнал зависит от семи параметров: амплитуды A=λ1, частоты ω2=λ2, начальной фазы ϕ=λ3, длительности импульса τи=λ4, момента его появления τ=λ5 относительно принятого отсчета времени и двух специфичных для радиотехники параметров: параметра формы l=λ6 и фазы всплеска ψ=λ7. Предполагается, что непосредственному наблюдению доступно только принимаемое колебание ξ(t). Относительно него до приема считаются известными следующие априорные сведения: 1) способ комбинирования сигнала и помехи, т.е. конкретный вид детерминированной и известной функции F(.), сигнал sel(t,λ) является детерминированной и известной функцией аргументов tи λ, 3) известны все необходимые для решения задачи вероятностные характеристики векторной случайной величины λ и помехи n(t). В дальнейшем будет рассмотрен частный вид функции F(.), когда колебание ξ(t) представляет собой сумму сигнала и помехи: ξ(t)=sel(t, λ)+n(t), 0≤t≤T. (1.1.3)
Задачи обнаружения и различения сигналов являются частным случаем общей задачи различения гипотез. Сначала приведем различные представления апостериорной вероятности двух возможных значений дискретного параметра, соответствующих двух гипотезам. Принятое колебание представляет собой сумму 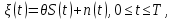 где n(t)- гауссовский белый шум; sel(t) – детерминированный селиусоидный сигнал, полностью расположенный на интервале наблюдения [0, T]. Параметр 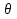 неизвестен и может принимать только одно из двух значений: неизвестен и может принимать только одно из двух значений: 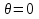 ( в принятом колебании сигнал отсутствует) и ( в принятом колебании сигнал отсутствует) и 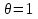 (в принятом колебании присутствует сигнал). (в принятом колебании присутствует сигнал).Что касается априорных сведений о параметре 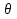 , то возможны два случая: 1) априорные вероятности , то возможны два случая: 1) априорные вероятности 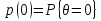 и и 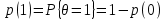 отсутствия и наличия сигнала известны; 2) эти априорные вероятности неизвестны. отсутствия и наличия сигнала известны; 2) эти априорные вероятности неизвестны. По принятой конкретной реализации 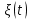 необходимо решить оптимальным образом, какое именно значение имеет параметр необходимо решить оптимальным образом, какое именно значение имеет параметр 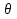 , т.е. присутствует или нет сигнал. Иначе говоря, нужно найти такой метод обработки принятого колебания , т.е. присутствует или нет сигнал. Иначе говоря, нужно найти такой метод обработки принятого колебания 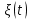 , который позволял бы наилучшим образом обнаруживать наличие сигнала на фоне шума. , который позволял бы наилучшим образом обнаруживать наличие сигнала на фоне шума.Решение может быть принято при двух взаимоисключающих условиях (гипотезах): условие 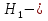 сигнал есть, сигнал есть,условие 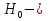 сигнала нет, сигнала нет,которые при выработке решения неизвестны. За счет помех и флуктуаций полезного сигнала каждому условию могут соответствовать два вида решений: решение 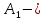 сигнал есть, сигнал есть,решение 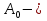 сигнала нет. сигнала нет.При обнаружении сигнала могут быть четыре ситуации: 1) 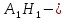 правильное обнаружение сигнала; правильное обнаружение сигнала;2) 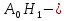 пропуск сигнала; пропуск сигнала;3) 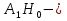 ложная тревога; ложная тревога;4) 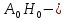 правильное необнаружение сигнала; правильное необнаружение сигнала; Имеется задача проверки двух гипотез: 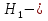 в реализации в реализации 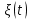 , за время наблюдения , за время наблюдения 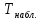 , присутствует сигнал , присутствует сигнал 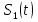 . .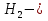 в реализации в реализации 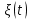 , за время наблюдения , за время наблюдения 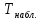 , присутствует сигнал , присутствует сигнал 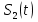 . .Причем, 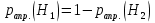 . .Перечисленным ситуациям соответствуют четыре вероятности совмещения событий, сумма которых равна единице: 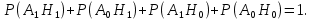 [13, с. 84] Каждому ошибочному решению ставиться в соответствие некоторая плата – стоимость ошибки 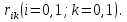 Для безошибочных решений эту стоимость условимся считать равной нулю Для безошибочных решений эту стоимость условимся считать равной нулю 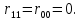 Тогда систему обнаружения можно характеризовать средней стоимостью (математическим ожиданием стоимости) ошибочных решений Тогда систему обнаружения можно характеризовать средней стоимостью (математическим ожиданием стоимости) ошибочных решений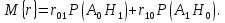 (2) (2)Лучшей из сравниваемых систем обработки можно тогда считать систему, удовлетворяющую критерию минимума этой стоимости, иначе – критерию минимума среднего риска. Критерий минимума среднего риска наиболее подходит для оценки помехоустойчивости различных типов сигналов. Для дальнейших рассуждений принимается, что стоимости ошибок 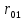 и и 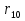 равны единице. Таким образом выражении (2) окончательно принимает вид равны единице. Таким образом выражении (2) окончательно принимает вид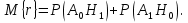 Априорные вероятности 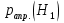 и и 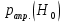 наличия и отсутствия сигнала являются известными. При этих условиях критерий минимума среднего риска переходит в критерий идеального наблюдателя. наличия и отсутствия сигнала являются известными. При этих условиях критерий минимума среднего риска переходит в критерий идеального наблюдателя.В соответствии с критерием идеального наблюдателя считается [10, с. 75], что верна гипотеза 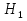 о наличии сигнала, если выполняется условие: о наличии сигнала, если выполняется условие: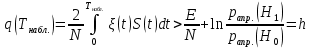 данное выражение приводится к следующему виду 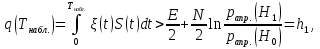 где 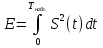 , , 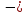 энергия сигнала; энергия сигнала;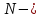 спектральная плотность шума; спектральная плотность шума;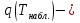 случайная величина, которая показывает значение на выходе коррелятора; случайная величина, которая показывает значение на выходе коррелятора;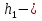 порог принятия решения. порог принятия решения.В случае симметричной системы передачи сигналов, когда имеется 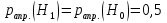 получается следующее условие: 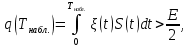 Тогда в соответствии с критерием идеального наблюдателя, для симметричной системы имеем следующее правило обнаружения детерминированного сигнала: - принимается решение о наличии сигнала 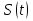 , т. е. верна гипотеза , т. е. верна гипотеза 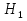 , если , если 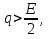 ; ;- принимается решение об отсутствии сигнала 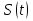 , т. е. верна гипотеза , т. е. верна гипотеза 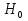 , если , если 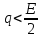 ; ;Функциональная схема приемного устройства осуществляющего обнаружение полностью детерминированного сигнала, приведена на рис. 2.2.1. [10, с. 69] 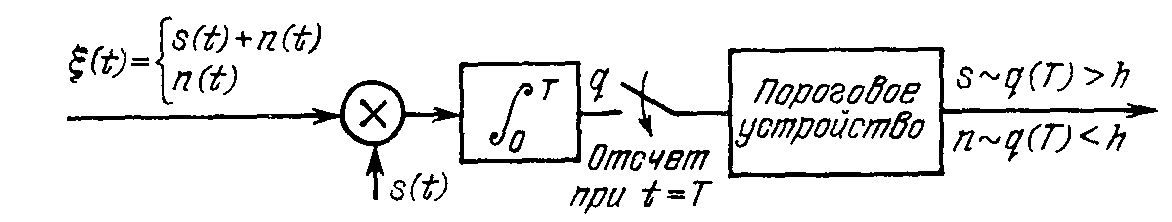 Оптимальный приемник обнаружения сигнала, изображенный на этом рисунке, представляет собой корреляционный приемник, дополненный пороговым устройством и синхронизаторам, позволяющими осуществить сравнение выборки выходного напряжения в момент времени t=T с пороговым уровнем h. Несмотря на то что для сравнения помехоустойчивости различных сигналов наилучшим является критерий идеального наблюдателя, в силу того, что на практике задача обнаружения чаще всего встречается в радиолокации, где априорные вероятности 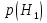 и и 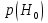 неизвестны, распространение получил критерий Неймана – Пирсона. Поэтому кривые обнаружения в известной литературе приводятся именно для этого критерия. неизвестны, распространение получил критерий Неймана – Пирсона. Поэтому кривые обнаружения в известной литературе приводятся именно для этого критерия.Критерий Неймана – Пирсона применяется в радиолокации для обнаружения сигнала, когда априорные вероятности 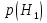 и и 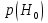 неизвестны. неизвестны.Согласно этому критерию оптимальный приемник должен максимизировать вероятность правильного обнаружения pd при заданной вероятности ложной тревоги 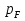 . Оптимальный алгоритм сводится к формированию отношения правдоподобия (2) или (5), причем величина порога . Оптимальный алгоритм сводится к формированию отношения правдоподобия (2) или (5), причем величина порога 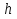 в правой части (5) выбирается по заданной вероятности ложной тревоги в правой части (5) выбирается по заданной вероятности ложной тревоги 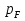 : :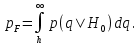 После этого вероятность правильного обнаружения вычисляется по формуле (7). |
