Дипломная работа с элементами исследования. Дипломная работа Разработка и исследование алгоритмов обнаружения сигналов с эллипсными несущими
 Скачать 1.79 Mb. Скачать 1.79 Mb.
|
2. Эллипсная тригонометрия2.1. Основные положенияКак известно, эллипс является более общей плоской фигурой, чем окружность, и представляет геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная. (Рис.2.1.) /4/.  Рис. 2.1. Связь эллипсной и классической тригонометрии На Рис 2.1. изображены эллипс, а также внешняя и внутренняя окружности эллипса. Отношение внутреннего и внешнего радиусов 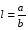 называется отношением полуосей эллипса. Оно является одним из основных его параметров. При 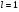 эллипс становится окружностью, при эллипс становится окружностью, при 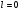 – прямой линией вдоль горизонтальной оси х. – прямой линией вдоль горизонтальной оси х.При b>a эллипс оказывается вытянутым вдоль вертикальной оси, т.е. повернутым на 90  . Однако . Однако 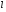 , как отношение малой полуоси к большой полуоси останется меньше единицы, а , как отношение малой полуоси к большой полуоси останется меньше единицы, а 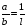 обозначим обозначим 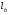 . Положение точки М на эллипсе принято выражать через угол . Положение точки М на эллипсе принято выражать через угол 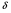 , т.е. , т.е. 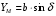 , , 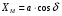 . . Эти зависимости имеют вид: 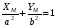 . . При движении точки М по эллипсу и точки М1 по большой окружности с постоянной угловой скоростью 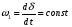 , где t – текущее время. Тогда , где t – текущее время. Тогда 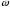 - угловая скорость движения точки М оказывается переменной. - угловая скорость движения точки М оказывается переменной. В ряде случаев движение точки М по эллипсу происходит с постоянной угловой скоростью 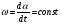 . Тогда угловая скорость . Тогда угловая скорость 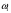 оказывается переменной и параметрическое уравнение эллипса, выраженное через угол оказывается переменной и параметрическое уравнение эллипса, выраженное через угол 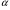 , оказывается усложненным. Эллипсная функция представляет собой новый вид функции, которая определяет координаты точки на эллипсе при ее движении с постоянной угловой скоростью , оказывается усложненным. Эллипсная функция представляет собой новый вид функции, которая определяет координаты точки на эллипсе при ее движении с постоянной угловой скоростью 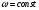 через текущий угол через текущий угол 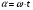 . .Таким образом, получается Эллипсная тригонометрия, являющаяся более общей теорией, чем круговая тригонометрия /5/. 2.2. Эллипсные функции и их связь с круговой тригонометрией.Эллипсные функции получаются следующим образом. В круговой тригонометрии синусоидальные функции основаны на уравнении окружности: 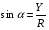 , , 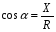 , ,где Y и X – координаты точки на окружности, R – радиус окружности. Аналогичные функции можно получить, если за основу брать эллипс, где угол 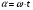 представляет собой текущую фазу, например, в электротехнике и радиотехнике. А представляет собой текущую фазу, например, в электротехнике и радиотехнике. А 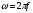 - представляет собой угловую частоту. При этом вертикальная координата Ym будет являться мгновенным значением эдс, напряжения или тока. Угол - представляет собой угловую частоту. При этом вертикальная координата Ym будет являться мгновенным значением эдс, напряжения или тока. Угол 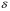 по отношению к углу по отношению к углу 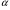 будет переменным, и зависимость между ними можно установить с Рис.2.1 Обозначим координату M1Xm=Ym1, а MXm=Ym . Тогда : будет переменным, и зависимость между ними можно установить с Рис.2.1 Обозначим координату M1Xm=Ym1, а MXm=Ym . Тогда : 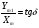 , а , а 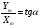 , откуда: , откуда: 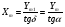 , т.е. , т.е.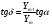 , , 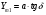 , , 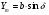 , поэтому , поэтому 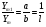 , следовательно, , следовательно,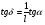 , , 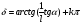 . . Здесь k=0 при 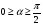 , k=1 при , k=1 при 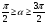 , k=2 при , k=2 при 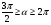 . .Таким образом: 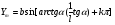 , ,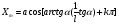 . .Такая форма записи координат точек на эллипсе сложна, и приводит к существенным усложнениям расчетов, поэтому введены новые функции, называемые соответственно эллипсными: синусом, косинусом, тангенсом: 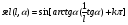 , ,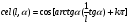 , , 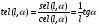 , ,аргументами которых являются угол 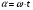 , и отношение полуосей , и отношение полуосей 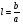 . .Из канонического уравнения получим: 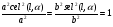 , откуда: , откуда: 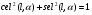 , , что являет собой новую форму канонического уравнения эллипса. Из уравнения (1.6) можем получить следующие зависимости /4/: 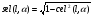 , ,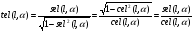 , ,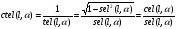 , , 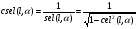 , ,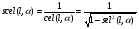 . .Здесь 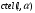 - котангенс эллипсный от - котангенс эллипсный от 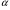 и и 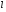 , , 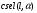 - косеканс эллипсный от - косеканс эллипсный от 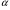 при l, при l, 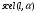 - секанс эллипсный от - секанс эллипсный от 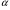 и и 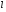 . .Связь эллипсных функций с классическими тригонометрическими функциями: 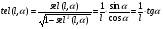 , ,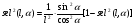 , ,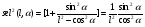 , ,откуда: 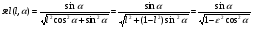 . . Здесь 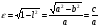 - эксцентриситет эллипса, c – фокусное расстояние (Рис. 2.1). - эксцентриситет эллипса, c – фокусное расстояние (Рис. 2.1).Аналогично получим: 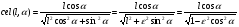 . . На основе этих формул можно получить и другие формулы: 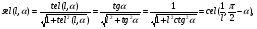 , , 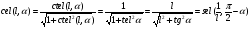 , , 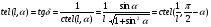 , , 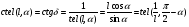 . . Из полученных формул не трудно заметить, что при 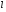 =1, т.е. переходе эллипса в окружность, эллипсная тригонометрия переходит в классическую круговую тригонометрию. =1, т.е. переходе эллипса в окружность, эллипсная тригонометрия переходит в классическую круговую тригонометрию.В выражениях (1.10) равенство 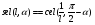 получено следующим образом: получено следующим образом: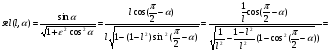 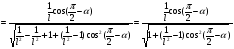 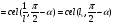 Аналогично выведено и равенство: 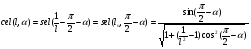 . . Здесь 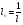 , ,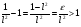 , и при малых , и при малых 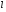 может достигать больших значений. может достигать больших значений.В функциях, где используется обратное отношение полуосей эллипса, т.е. 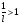 , оно заменено для упрощения записей , оно заменено для упрощения записей 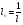 . .На рис.2.2., 2.3, 2.4 построены графики эллипсных функций. Здесь наглядно видно, что эллипсные функции охватывают широкий класс несинусоидальных периодических кривых, начиная с прямоугольных функций при l=0. До бесконечно узких импульсов при l→∞, включая круговые синусоидальные, трапециевидные, треугольные, кривые, описываемые простыми формулами в виде эллипсных функций. Таким образом, круговые синусоидальные функции оказываются частью эллипсной тригонометрии /6/. 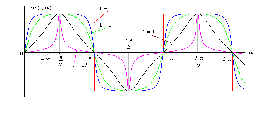 Рис. 2.2. График эллипсного синуса 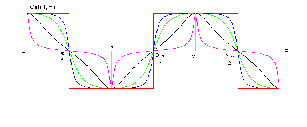 Рис. 2.3. График эллипсного косинуса На рис.2.4.а показан график эллипсного тангенса, который аналогичен по форме моноциклу Гаусса, показанном на рис. 2.4.б. 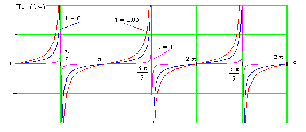 Рис. 2.4.а График эллипсного тангенса 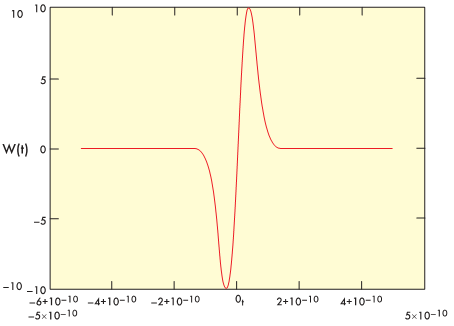 Рис.2.4.б. Вид моноцикла Гаусса (длительность 50 пс) Таким образом, математическое описание моноцикла Гаусса эллипсным тангенсом позволит управлять формой моноцикла путем изменения параметров эллипсного тангенса. На рис. 2.5 и 2.6. показаны в увеличенном масштабе графики эллипсных функций в пределах 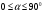 при конкретных значениях при конкретных значениях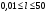 . .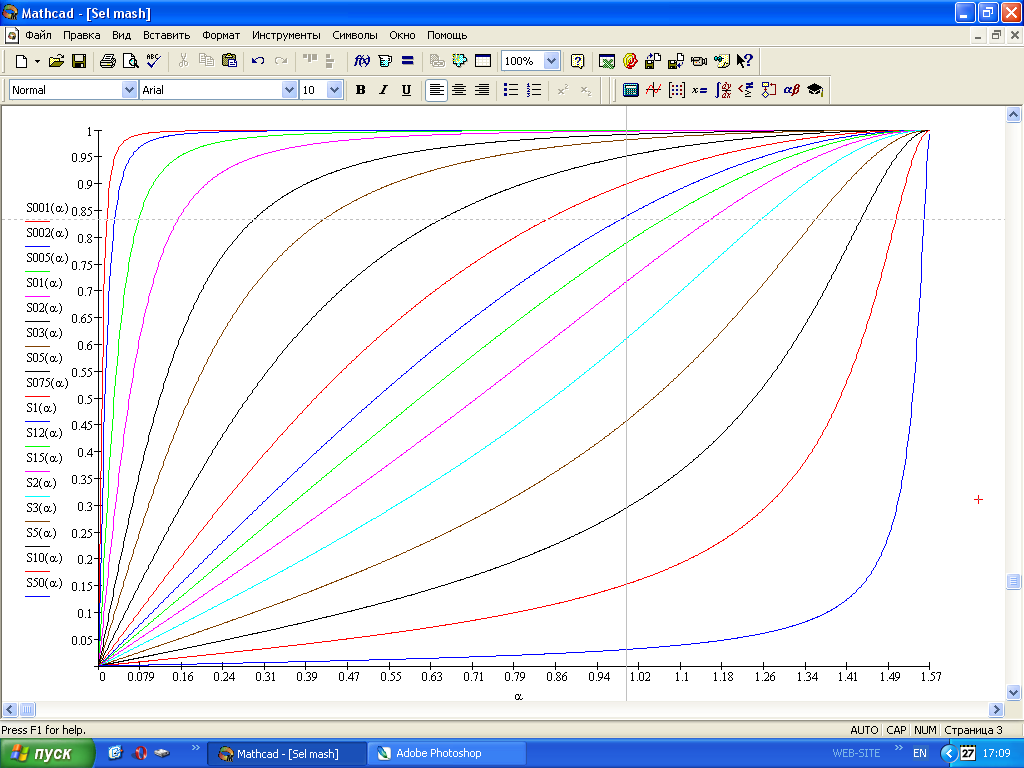 Рис. 2.5. Временные диаграммы эллипсного синуса в увеличенном масштабе. 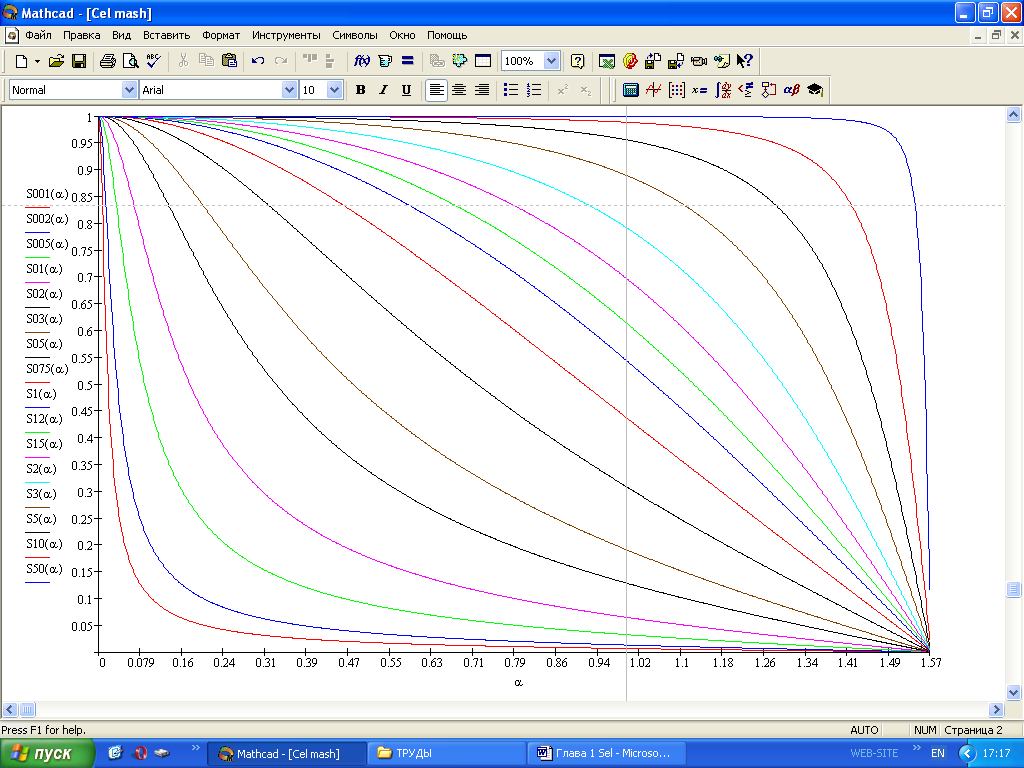 Рис. 2.6. Временные диаграммы эллипсного косинуса в увеличенном масштабе. Функции, обратные эллипсным синусу и косинусу имеют вид, представленный на рис. 2.7 и рис.2.8. 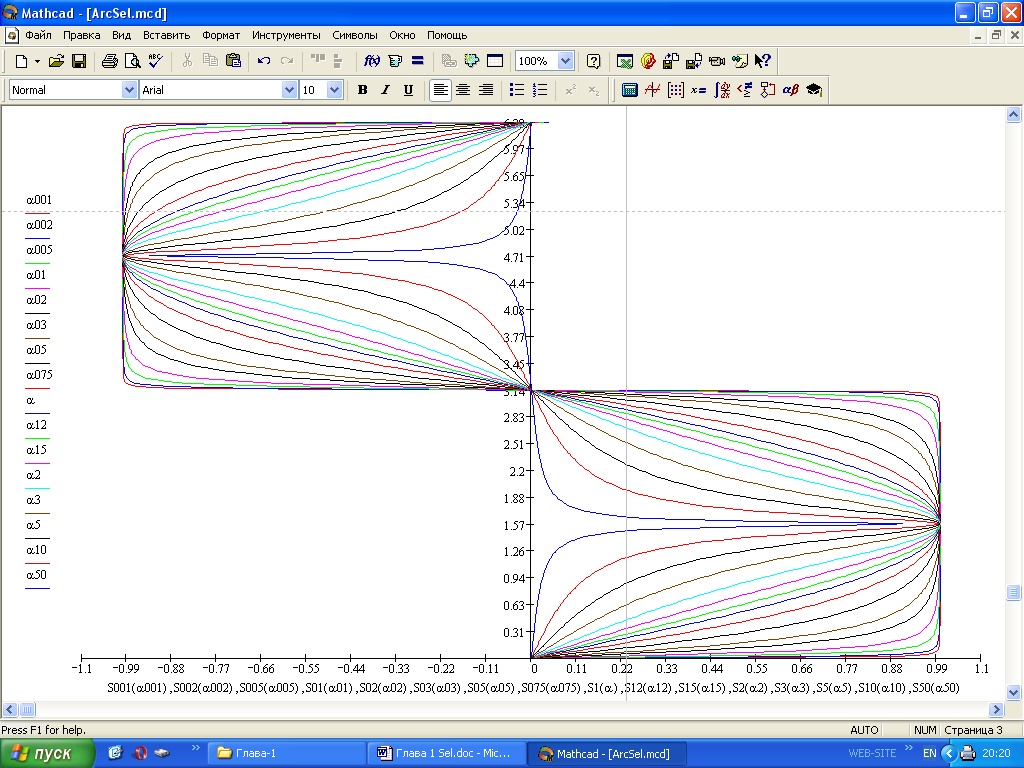 Рис.2.7. График арксинуса эллипсного  Рис.2.8. График арккосинуса эллипсного |
