Дипломная работа с элементами исследования. Дипломная работа Разработка и исследование алгоритмов обнаружения сигналов с эллипсными несущими
 Скачать 1.79 Mb. Скачать 1.79 Mb.
|
2.3. Селиус. Разнообразие форм селиусоидального колебанияОбъектом исследований для последующих частей дипломной работы из всего многообразия эллипсных функций был выбран эллипсный синус, который задается следующей формулой: 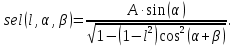 Для краткости эллипсный синус будет называться селиусом. Получается, что селиус является псевдонимом эллипсного синуса. Сигналом называется изменяющаяся во времени физическая величина, отображающая передаваемое сообщение. Поэтому представим селиус во временной области следующим образом: 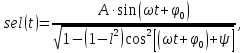 где А – амплитуда, ω – частота, φ0 – начальная фаза, 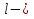 параметр формы, параметр формы, 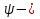 фаза всплеска, фаза всплеска,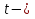 время. время. По аналогии с синусоидой колебание, реализуемое во времени, будет называться селиусоидой. Таким образом, селиусоида– это временной колебательный процесс, изменяющийся по закону селиуса. В последующих частях дипломной работы будут рассмотрены только функции, представляющие собой селиус с различными параметрами. Именно селиус будет рассматриваться в качестве несущего колебания. Полученная функция является пятипараметрическим обобщением гармонической функций, впервые предложенного Ч. И. Мастюковым, построенного путем специфической суперпозиции двух трехпараметрических гармонических функций с добавлением к традиционным для гармонических колебаний в радиотехнике амплитудой А, угловой частотой ω и начальной фазой φ0 и еще двух параметров, от которых зависит форма сигнала – параметра формы 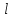 и фазы всплеска и фазы всплеска 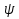 . Селиус имеет богатое разнообразие форм в зависимости от параметра формы и фазы всплеска. В частности при . Селиус имеет богатое разнообразие форм в зависимости от параметра формы и фазы всплеска. В частности при 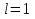 и и 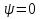 , он становится синусоидой. При других значениях своих специфических параметров селиус может быть использован в качестве сложного колебания. [3] , он становится синусоидой. При других значениях своих специфических параметров селиус может быть использован в качестве сложного колебания. [3]На рис.2.9 показаны осциллограммы селиуса при фазе всплеска 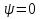 и при следующих значениях параметра формы: и при следующих значениях параметра формы: 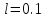 , , 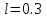 , , 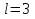 , , 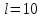 . . 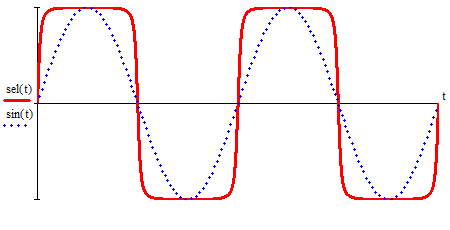 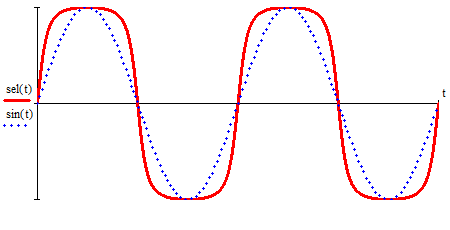 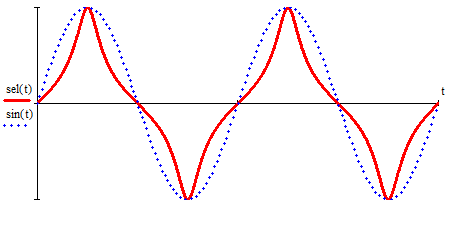 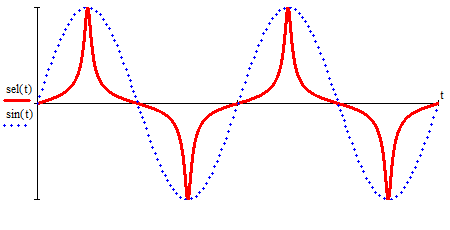 рис.2.9 Видно, что колебание расширяется и стремится к меандру, при стремлении параметра формы к нулю, и наоборот, при увеличении l, колебание «сужается». На рис.2.10 на двух верхних графиках показаны осциллограммы селиуса при параметре формы 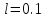 и при следующих значениях фазывсплеска и при следующих значениях фазывсплеска 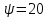 и и 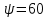 , а на двух нижних графиках показаны осциллограммы селиуса при параметре формы , а на двух нижних графиках показаны осциллограммы селиуса при параметре формы 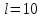 и таких же значениях фазы всплеска и таких же значениях фазы всплеска 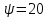 и и 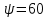 . .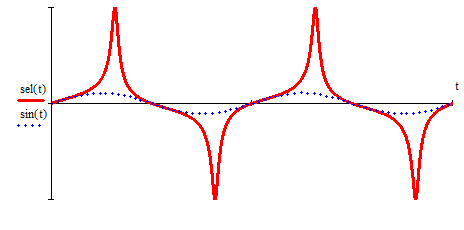 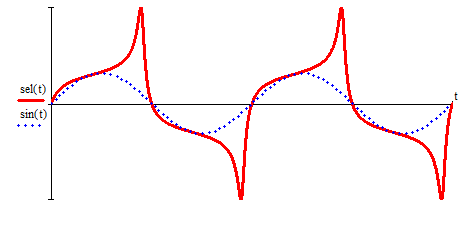 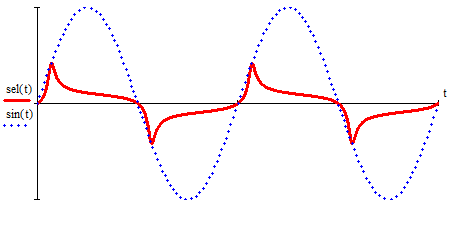 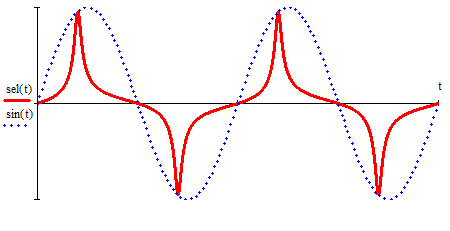 рис.2.10 Из графиков следует, что колебание меняет свой вид (форму) в зависимости от фазы всплеска, при этом также меняется амплитуда колебания. На рис.2.11показаны графики селиусоидального колебания при изменении параметра формы 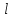 от 0.01 до 1000 и фазе всплеска равной нулю. от 0.01 до 1000 и фазе всплеска равной нулю.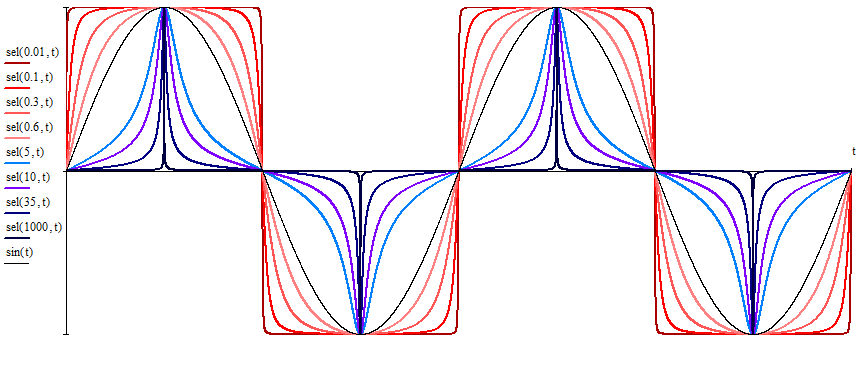 Осциллограммы sel(t) в зависимости от параметра формы l, при ψ= 0. рис.2.11 По графику можно заметить, что при 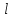 стремящемся к бесконечности селиус «ссужается» до дельта импульса, а при стремящемся к бесконечности селиус «ссужается» до дельта импульса, а при 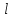 стремящемся к нулю он «расширяется» до меандра. стремящемся к нулю он «расширяется» до меандра.На рис.2.12 показаны осциллограммы селиуса при параметре формы 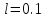 и при значениях фазы всплеска и при значениях фазы всплеска 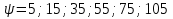 и и 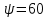 , а на рис.2.13 показаны осциллограммы селиуса при параметре формы , а на рис.2.13 показаны осциллограммы селиуса при параметре формы 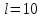 и таких же значениях фазы всплеска и таких же значениях фазы всплеска 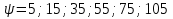 . .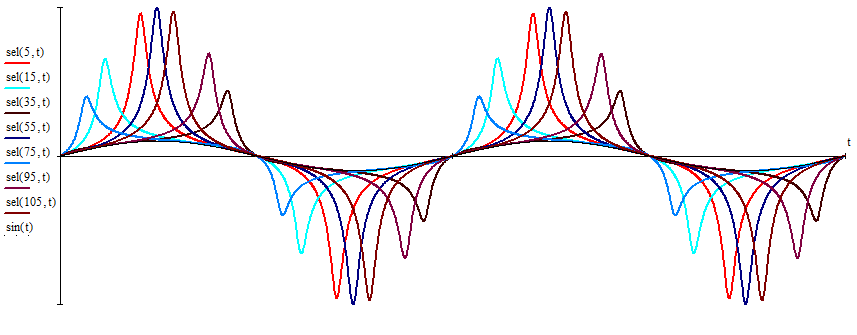 Осциллограммы sel(t) в зависимости от фазы всплеска, при l = 0,1. рис.2.12 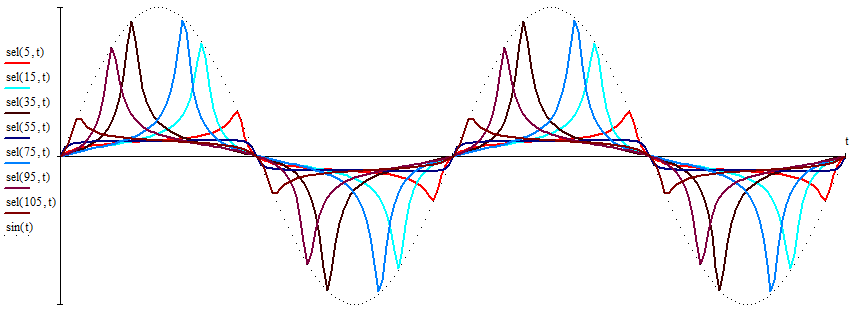 Осциллограммы sel(t) в зависимости от фазы всплеска, при l = 10. рис.2.13 Выводы:
Поскольку в данной дипломной работе впервые предлагается использование эллипсных функций (селиусоиды) в качестве несущего колебания, то необходимо исследовать их радиофизические свойства. В свою очередь исследование радиофизических характеристик необходимо для ответа на вопрос о возможности использования данного типа колебаний на практике. |
