Кейс. Дисциплина Управление проектом Кейс

• Название: Дисциплина Управление проектом Кейс
• Дата: 04.12.2022
• Размер: 183.74 Kb.
• Имя файла: Кейс.docx
• Тип: Исследование; #827396

Автономная некоммерческая образовательная организация высшего образования

«Сибирский институт бизнеса и информационных технологий»

Зачетная работа

7 семестра

Дисциплина: Управление проектом

Кейс

Выполнил(а):

Рыбалкин Алексей Олегович

(Ф.И.О. студента)

______________________________

(направление, группа)

Проверил(а):

_____________________________

(Ф.И.О. преподавателя)

_____________________________

(дата)

Омск 2022 г


Задание

Администрация компании "Satumite pie" собирается реализовать исследовательский проект по изучению характеристик нового продукта. Итогом выполнения проекта должен быть отчет, содержащий рекомендации по выпуску нового продукта. Ниже приведены операции, которые необходимо осуществить в процессе выполнения исследовательского проекта:

Операция	Описание	Непосредственно предшествующие операции	Ожидаемое время выполнения, дней	Потребнос- ти в персонале
А В С D Е F G Н I J	Первичные разработки Исследование рынка Получение технических стандартов Создание образца Подготовка рыночной базы Расчет стоимости Испытание продукта Выборочный контроль Оценки цены Итоговый отчет	— — А А А С D В, Е Н F,G, I	5 3 2 5 3 2 4 6 2 6	3 2 2 5 3 2 5 4 1 2

Требуется:

1. 
   Построить сетевой граф, отражающий приведенные выше операции и их взаимосвязи. Определить критический путь и наименьшую продолжительность выполнения проекта.
   
2. 
   В предположении, что началом выполнения проекта служит нулевой момент времени, а каждая операция начинается с наиболее раннего срока, построить график, изображающий потребности в персонале на любой момент времени.
   
3. 
   Администрация компании приняла решение, что на выполнение изложенного проекта в любой момент времени будет выделено не более 9 человек персонала. Опишите, как следует выполнять проект в данных условиях за наименьшее время, найденное в п 1. В течение какого количества недель в выполнении проекта будут участвовать все 9 человек персонала?
   

Решение

В нашем задании продолжительность выполнения работы задаётся двумя оценками – минимальная и максимальная. Минимальная оценка t_min(i,j) характеризует продолжительность выполнения работы при наиболее благоприятных обстоятельствах, а максимальная t_max(i,j) – при наиболее неблагоприятных условиях.

Продолжительность работы в этом случае рассматривается, как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение t_ож(i,j) оценивается по формуле:

t_ож(i,j)=(3 t_min(i,j)+2 t_max(i,j))/5

Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии:
S²(i,j)=0,04(t_max(i,j)-t_min(i,j))²

Рассчитаем ожидаемое значение и показатель дисперсии.
t_ож(1,1)=(3*5+2*5)/5=4.2
t_ож(1,1)=(3*3+2*3)/5=2.6
t_ож(3,1)=(3*2+2*2)/5=2
t_ож(4,1)=(3*5+2*5)/5=5
t_ож(5,3)=(3*3+2*3)/5=3
t_ож(6,3)=(3*2+2*2)/5=2
t_ож(7,2)=(3*4+2*4)/5=4.4
t_ож(8,7)=(3*6+2*6)/5=5.2
t_ож(9,8)=(3*2+2*2)/5=1.6
t_ож(10,9)=(3*6+2*6)/5=4.4
S²(1,1)=0.04(3-5)²=0.16
S²(1,1)=0.04(2-3)²=0.04
S²(3,1)=0.04(2-2)²=0
S²(4,1)=0.04(5-5)²=0
S²(5,3)=0.04(3-3)²=0
S²(6,3)=0.04(2-2)²=0
S²(7,2)=0.04(5-4)²=0.04
S²(8,7)=0.04(4-6)²=0.16
S²(9,8)=0.04(1-2)²=0.04
S²(10,9)=0.04(2-6)²=0.64
Полученные данные занесем в таблицу.

Работа (i,j)	tmin(i,j)	tmax(i,j)	m(i,j)	Ожидаемая продолжительность tож(i,j)	Дисперсия S2(i,j)
1,1	5	3	0	4.2	0.16
1,1	3	2	0	2.6	0.04
3,1	2	2	0	2	0
4,1	5	5	0	5	0
5,3	3	3	0	3	0
6,3	2	2	0	2	0
7,2	4	5	0	4.4	0.04
8,7	6	4	0	5.2	0.16
9,8	2	1	0	1.6	0.04
10,9	6	2	0	4.4	0.64

Используя полученные данные, мы можем найти основные характеристики сетевой модели табличным методом, критический путь и его продолжительность.

Расчет сроков свершения событий.

Для i=1 (начального события), очевидно tp(1)=0.

i=2: t^p(2) = t^p(1) + t(1,2) = 0 + 0 = 0.

i=3: t^p(3) = t^p(2) + t(2,3) = 0 + 0 = 0.

i=4: t^p(4) = t^p(3) + t(3,4) = 0 + 0 = 0.

i=5: t^p(5) = t^p(4) + t(4,5) = 0 + 0 = 0.

i=6: t^p(6) = t^p(5) + t(5,6) = 0 + 0 = 0.

i=9: t^p(9) = t^p(8) + t(8,9) = 0 + 0 = 0.

Длина критического пути равна раннему сроку свершения завершающего события 9: t_kp=tp(9)=0

При определении поздних сроков свершения событий t_п(i) двигаемся по сети в обратном направлении, то есть справа налево и используем формулы (3), (4).

Для i=9 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): t^п(9)= t^р(9)=0

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 8. Просматриваются все строчки, начинающиеся с номера 8.

(8,7): 0 - 5.2 = -5.2; i=8: min(t^п(9) - t(8,9);t^п() - t) = min(1.6 - 0; - ) = 0.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 7. Просматриваются все строчки, начинающиеся с номера 7. (7,2): 0 - 4.4 = -4.4;

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Просматриваются все строчки, начинающиеся с номера 2.

(2,3): 0 - 0 = 0;

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Просматриваются все строчки, начинающиеся с номера 3.

(3,1): 0 - 2 = -2;

(3,4): 0 - 0 = 0;

i=3: min(t^п() - t;t^п() - t) = min( - ; - ) = 0.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 6. Просматриваются все строчки, начинающиеся с номера 6.

(6,3): 0 - 2 = -2;

(3,1): 0 - 2 = -2;

(3,4): 0 - 0 = 0;

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Просматриваются все строчки, начинающиеся с номера 5.

(5,3): 0 - 3 = -3;

(5,6): 0 - 0 = 0;

i=5: min(t^п() - t;t^п() - t) = min( - ; - ) = 0.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 1. Просматриваются все строчки, начинающиеся с номера 1.

(1,2): 0 - 0 = 0;

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Просматриваются все строчки, начинающиеся с номера 4.

(4,1): 0 - 5 = -5;

(4,5): 0 - 0 = 0;

i=4: min(t^п() - t;t^п() - t) = min( - ; - ) = 0.

(1,2): 0 - 0 = 0;

(3,1): 0 - 2 = -2;

(3,4): 0 - 0 = 0;

(2,3): 0 - 0 = 0;

(1,2): 0 - 0 = 0;

Расчет резерва событий

Номер события	Сроки свершения события: ранний tp(i)	Сроки свершения события: поздний tп(i)	Резерв времени, R(i)
1		0	0
2	0	0	0
3	0	0	0
4	0	0	0
5	0	0	0
6	0	0	0
7		0	0
8		0	0
9	0	0	0

Находим полный резерв R^П_i-j = Tп_j-t_i-j-Tр_i

R^П_(1,2) = 0-0-0 = 0

R^П_(2,3) = 0-0-0 = 0
R^П_(3,1) = 0-2-0 = -2
R^П_(3,4) = 0-0-0 = 0
R^П_(4,1) = 0-5-0 = -5
R^П_(4,5) = 0-0-0 = 0
R^П_(5,3) = 0-3-0 = -3
R^П_(5,6) = 0-0-0 = 0
R^П_(6,3) = 0-2-0 = -2
R^П_(7,2) = 0-4.4-0 = -4.4
R^П_(8,7) = 0-5.2-0 = -5.2
R^П_(8,9) = 1.6-0-0 = 1.6
R^П_(9,8) = 0-1.6-0 = -1.6
Свободный резерв времени также можно найти и по формуле R^C_i-j = Tп_i-t_i-j-Tр_i
R^C_(1,2) = 0-0-0 = 0
R^C_(2,3) = 0-0-0 = 0
R^C_(3,1) = 0-2-0 = -2
R^C_(3,4) = 0-0-0 = 0
R^C_(4,1) = 0-5-0 = -5
R^C_(4,5) = 0-0-0 = 0
R^C_(5,3) = 0-3-0 = -3
R^C_(5,6) = 0-0-0 = 0
R^C_(6,3) = 0-2-0 = -2
R^C_(7,2) = 0-4.4-0 = -4.4
R^C_(8,7) = 0-5.2-0 = -5.2
R^C_(8,9) = 1.6-0-0 = 1.6
R^C_(9,8) = 0-1.6-0 = -1.6
Независимый резерв времени также можно найти и по формуле R^Н_i-j = Tр_j-t_i-j-Tп_i
R^Н_(1,2) = 0-0-0 = 0
R^Н_(2,3) = 0-0-0 = 0
R^Н_(3,1) = 0-2-0 = -2
R^Н_(3,4) = 0-0-0 = 0
R^Н_(4,1) = 0-5-0 = -5
R^Н_(4,5) = 0-0-0 = 0
R^Н_(5,3) = 0-3-0 = -3
R^Н_(5,6) = 0-0-0 = 0
R^Н_(6,3) = 0-2-0 = -2
R^Н_(7,2) = 0-4.4-0 = -4.4
R^Н_(8,7) = 0-5.2-0 = -5.2
R^Н_(8,9) = 1.6-0-0 = 1.6
R^Н_(9,8) = 0-1.6-0 = -1.6
Анализ сетевой модели по времени

Работа (i,j)	Количество предшествующих работ	Продолжительность tij	Ранние сроки: начало tijР.Н.	Ранние сроки: окончание tijР.О.	Поздние сроки: начало tijП.Н.	Поздние сроки: окончание tijП.О.	Резервы времени: полный RijП	Независимый резерв времени RijН	Частный резерв I рода, Rij1	Частный резерв II рода, RijC
(1,2)	0	0	0	0	0	0	0	0	0	0
(2,3)	1	0	0	0	0	0	0	0	0	0
(3,1)	1	2	0	2	-2	0	-2	-2	-2	-2
(3,4)	1	0	0	0	0	0	0	0	0	0
(4,1)	1	5	0	5	-5	0	-5	-5	-5	-5
(4,5)	1	0	0	0	0	0	0	0	0	0
(5,3)	1	3	0	3	-3	0	-3	-3	-3	-3
(5,6)	1	0	0	0	0	0	0	0	0	0
(6,3)	1	2	0	2	-2	0	-2	-2	-2	-2
(7,2)	0	4.4	0	4.4	-4.4	0	-4.4	-4.4	-4.4	-4.4
(8,7)	0	5.2	0	5.2	-5.2	0	-5.2	-5.2	-5.2	-5.2
(8,9)	0	0	0	0	1.6	1.6	1.6	1.6	1.6	1.6
(9,8)	1	1.6	0	1.6	-1.6	0	-1.6	-1.6	-1.6	-1.6

Критический путь: (1,2)

Продолжительность критического пути: 0

Расчет наиболее ранних сроков начала окончания операций

Операция	Продолжительность, дней	Наиболее ранний срок начала	Наиболее ранний срок окончания	Комментарии
A B C D E F G H I J	5 3 2 5 3 2 4 6 2 6	0 0 5 5 5 7 10 8 14 16	0+5=5 0+3=3 5+2=7 5+5=10 5+3=8 7+2=9 10+4=14 8+6=14 14+2=16 16+6=22	Нельзя начать, пока не завершена А Нельзя начать, пока не завершена А Нельзя начать, пока не завершена А Нельзя начать, пока не завершена С Нельзя начать, пока не завершена D Нельзя начать, пока не завершены В и E Нельзя начать, пока не завершена Н Нельзя начать, пока не завершены F,G, I. Из них берется самая длительная, т.к. нужно начинать J, когда завершены уже все три

Расчет наиболее поздних сроков начала и окончания

Операций

Операция	Продолжительность, дней	Наиболее Поздний срок окончания	Наиболее Поздний Срок Начала	Комментарии
J I H G F E D C B A	6 2 6 4 2 3 5 2 3 5	22 16 14 16 16 8 12 14 8 5	22-6=16 16-2=14 14-6=8 16-4=12 16-2=14 8-3=5 12-5=7 14-2=12 8-3=5 5-5=0	I нужно завершить до наступления наиболее позднего срока начала J H нужно завершить до наступления наиболее позднего срока начала I G нужно завершить до наступления наиболее позднего срока начала J F нужно завершить до наступления наиболее позднего срока начала J E нужно завершить до наступления наиболее позднего срока начала H D нужно завершить до наступления наиболее позднего срока начала G C нужно завершить до наступления наиболее позднего срока начала F. В нужно завершить до наступления наиболее позднего срока начала H А нужно завершить до наступления наиболее позднего срока начала C, D, E. Нужно использовать наименьший из этих сроков, равным 5 дням.

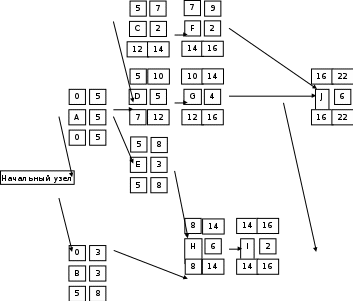С
4

14

7
етевая модель имеет критический путь А-E-H-I-J.




С

2




5

F

5




2




1

2

А

D

5




G

5




0

5

4

12

10




E

J

3

7




8

6




0

I




В

Н

3

2

16

16

22

22




3

6




6




8

8

14

14


График Ганта


Потребности в персонале




F

J

9

16

22

(2)

(5)

(1)

(2)

25



С




Е

7

3

8

(2)

(3)



В



(2)




D

G



H

10

14

14

(5)

(4)



А

I




Время, дни

5

(3)


5

15

20

10

График потребности в персонале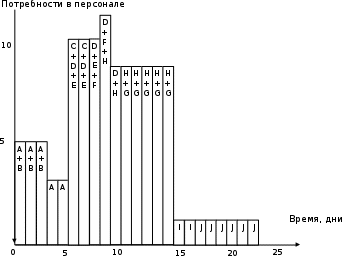



Список использованной литературы

1. 
   Зуховицкий С. И., Радчик И. А., Математические методы сетевого планирования, М., 2015. - 500 с.
   
2. 
   Модер Дж., Филлипс С., Метод сетевого планирования в организации работ, пер. с англ., М., 2017. – 320 с.
   
3. 
   Основные положения по разработке и применению систем сетевого планирования и управления, 2 изд., М., 2016. – 302 с.
   
4. 
   Сетевые графики в планировании, М., 2016. – 117 с.
   
5. 
   Сетевые модели и задачи управления, М., 2014. – 298 с.