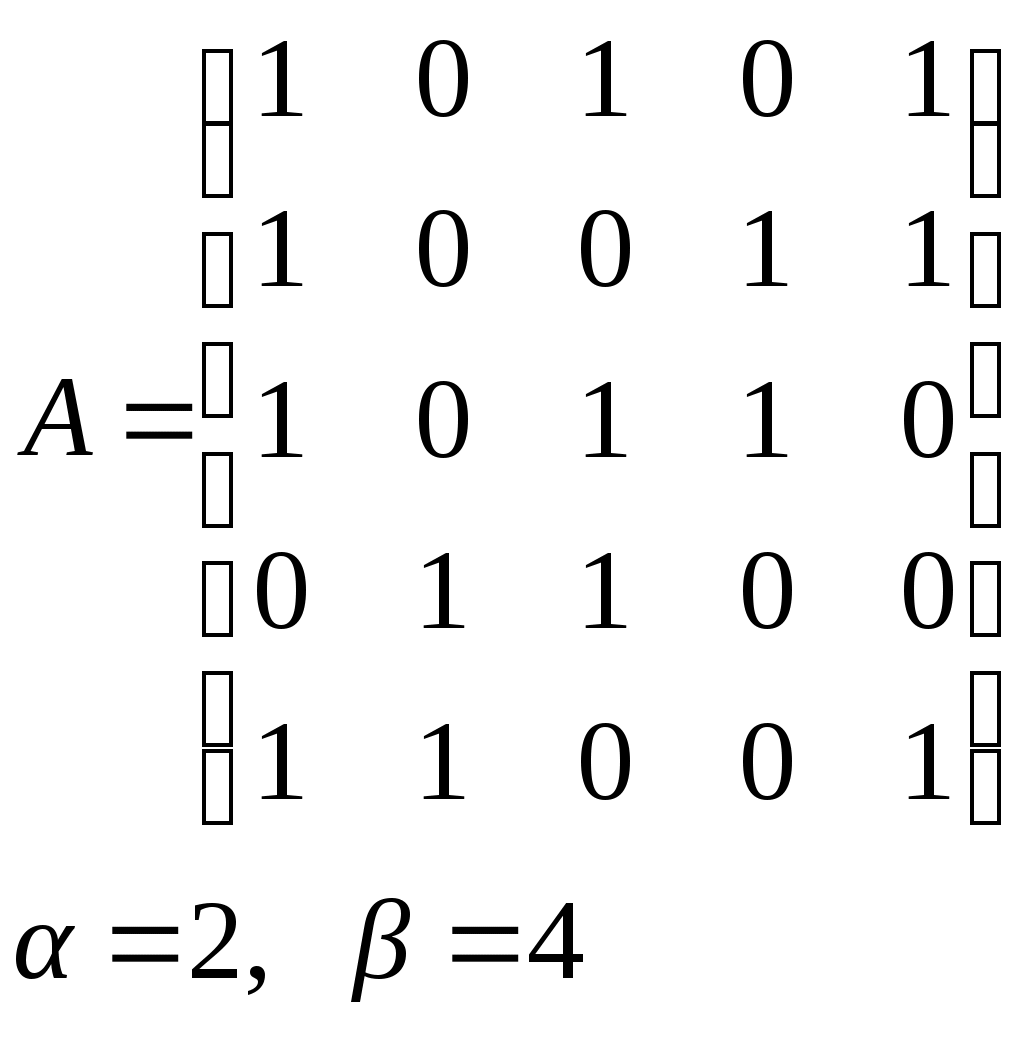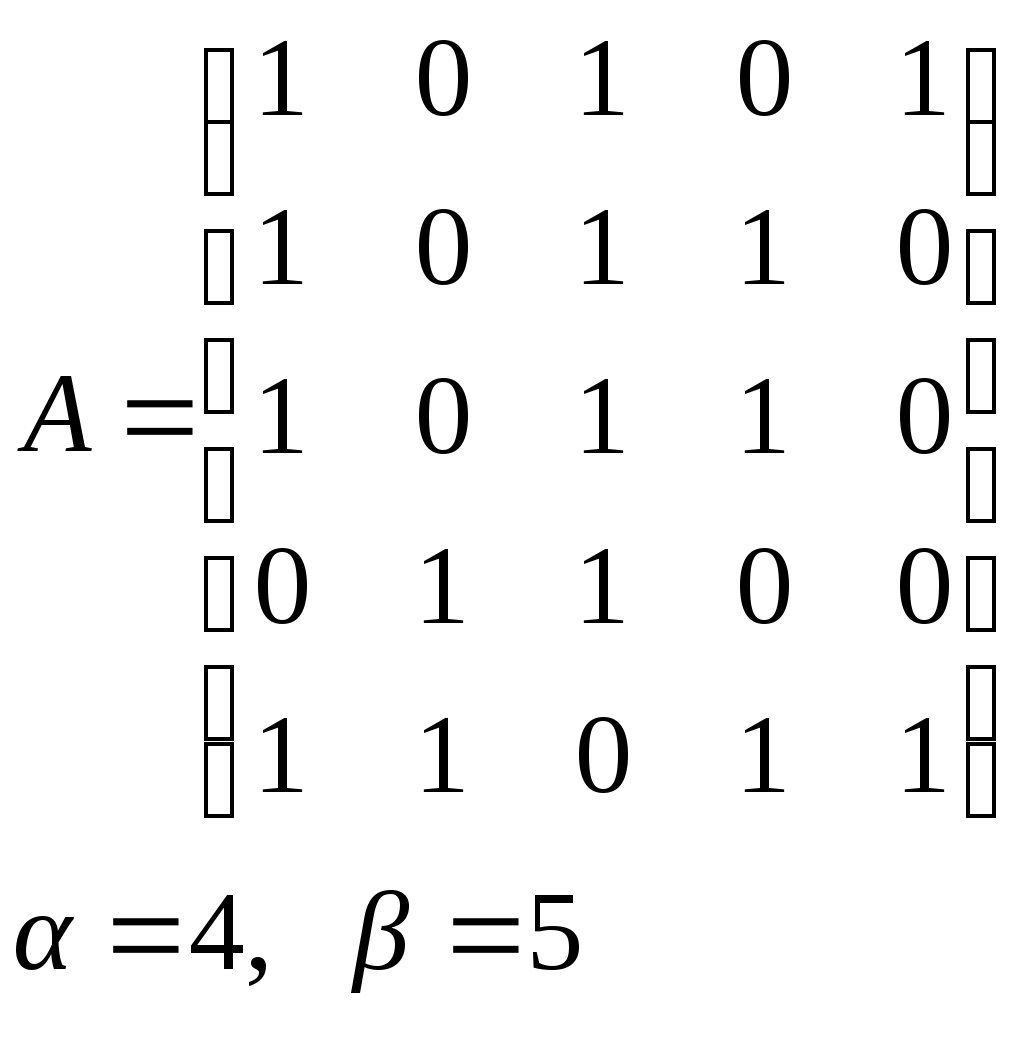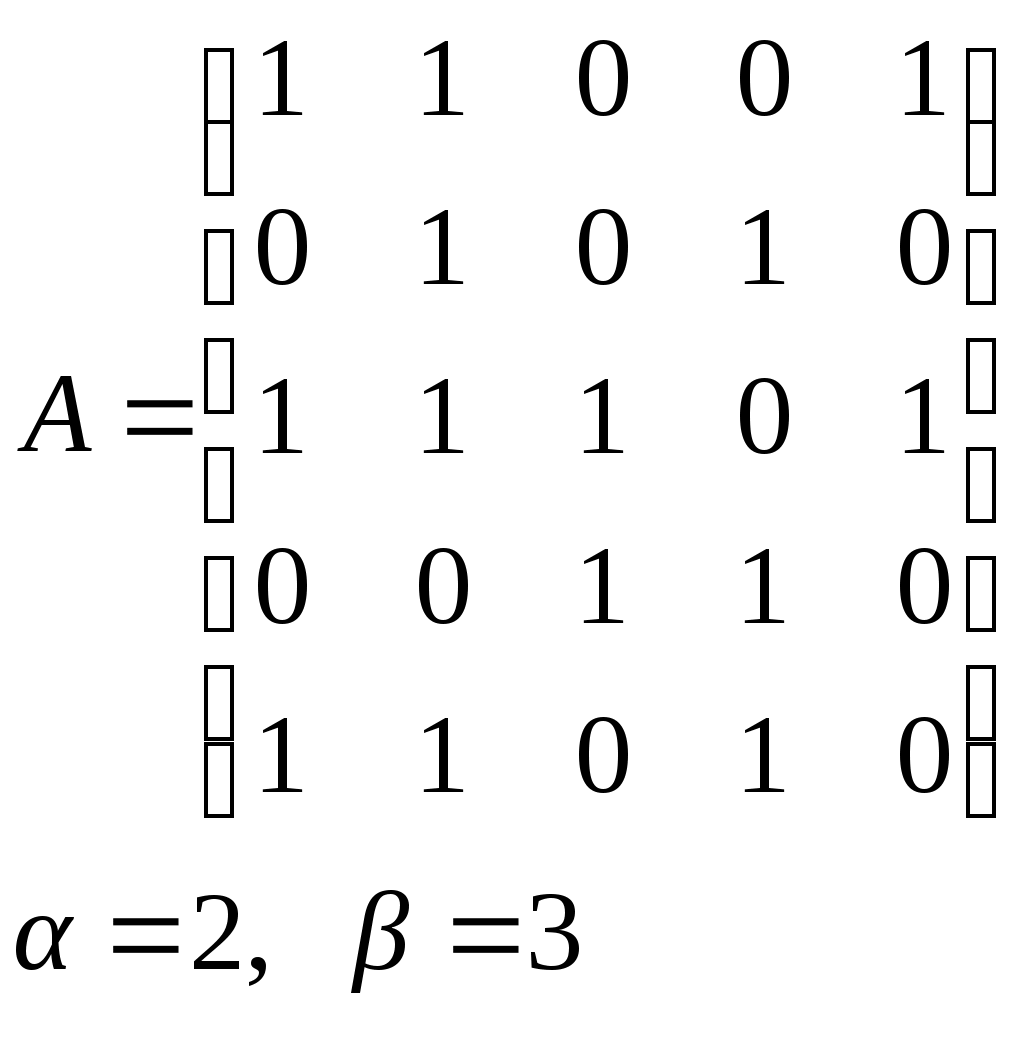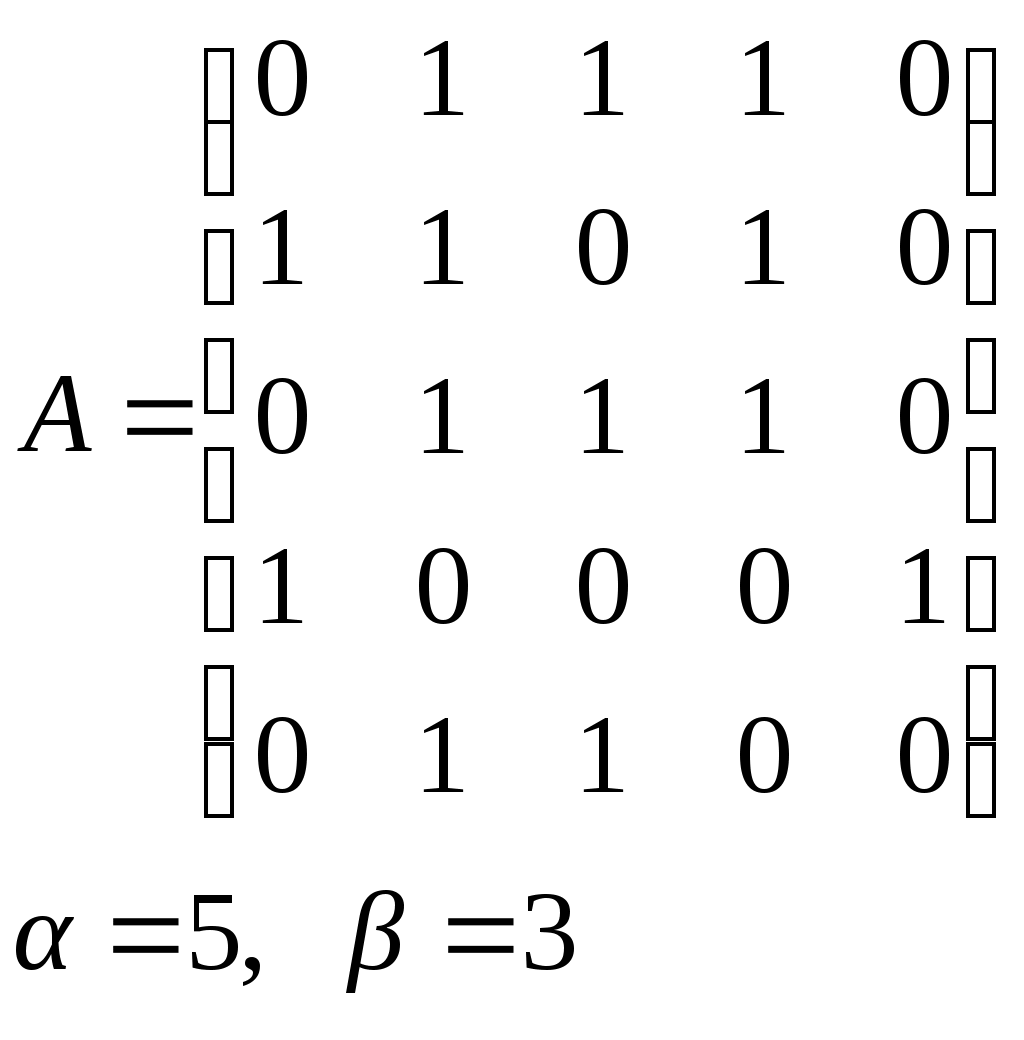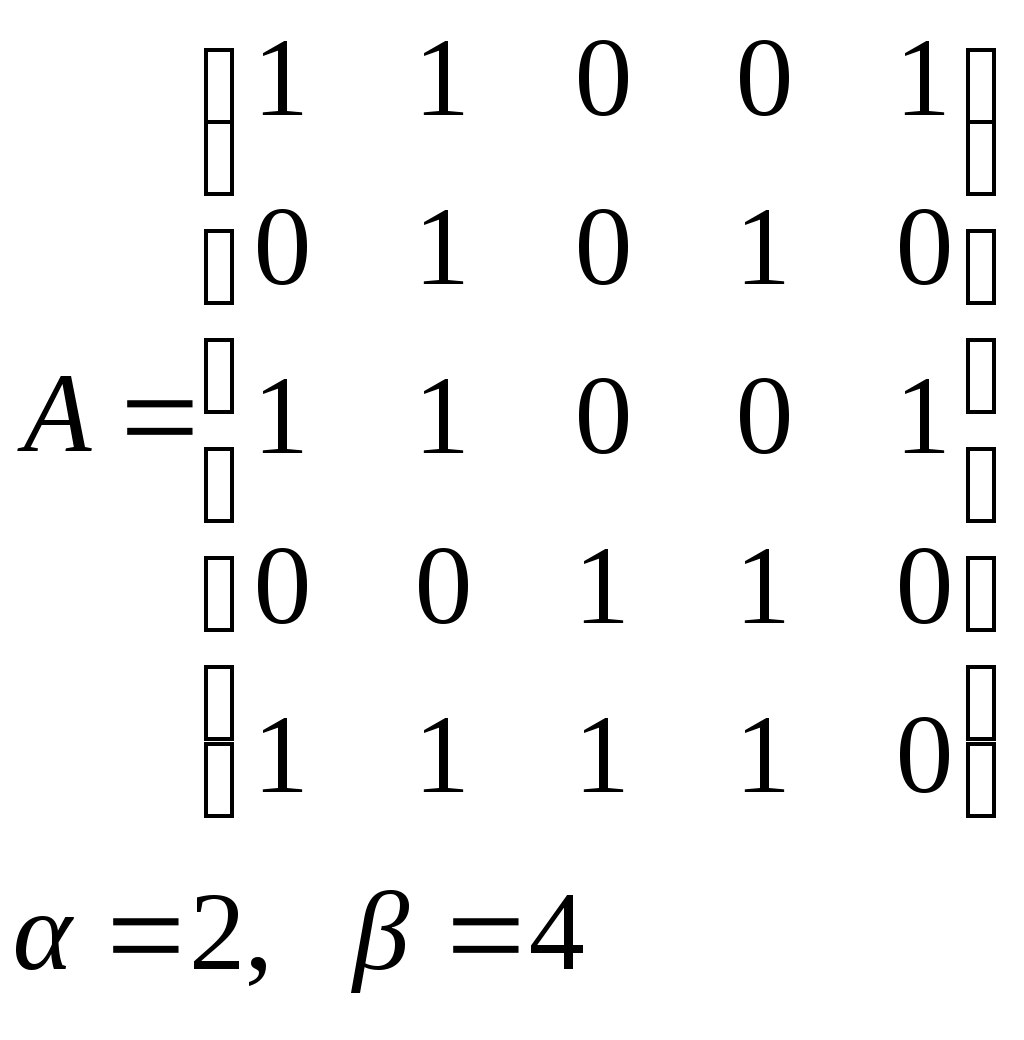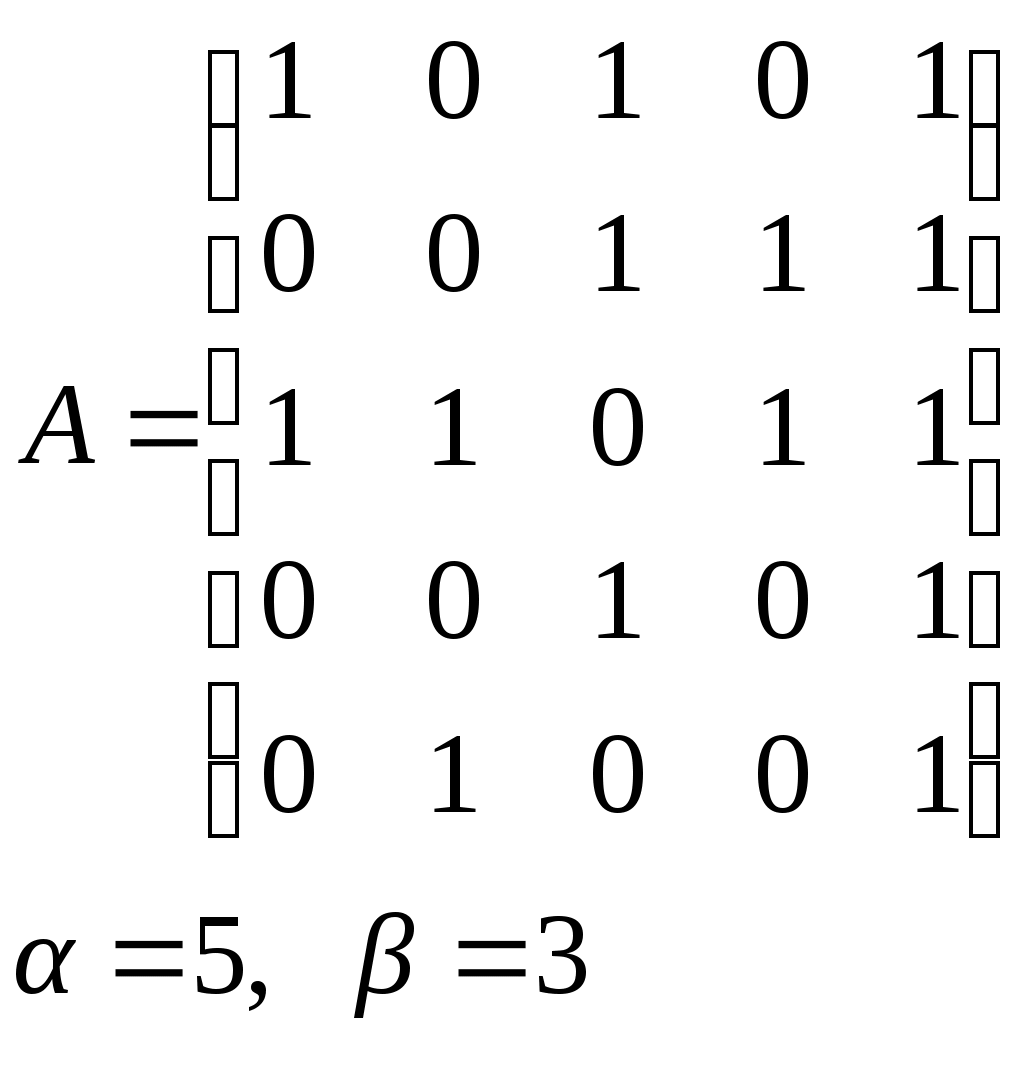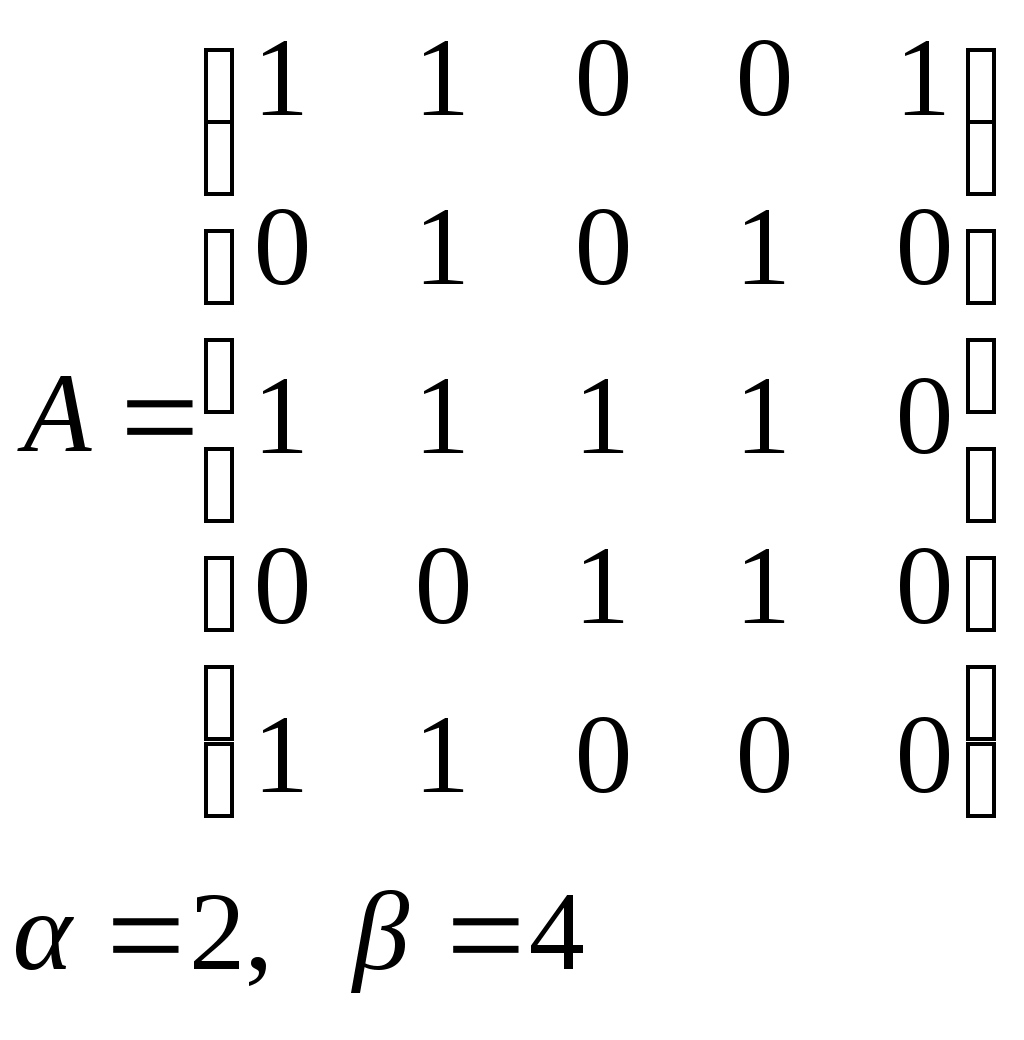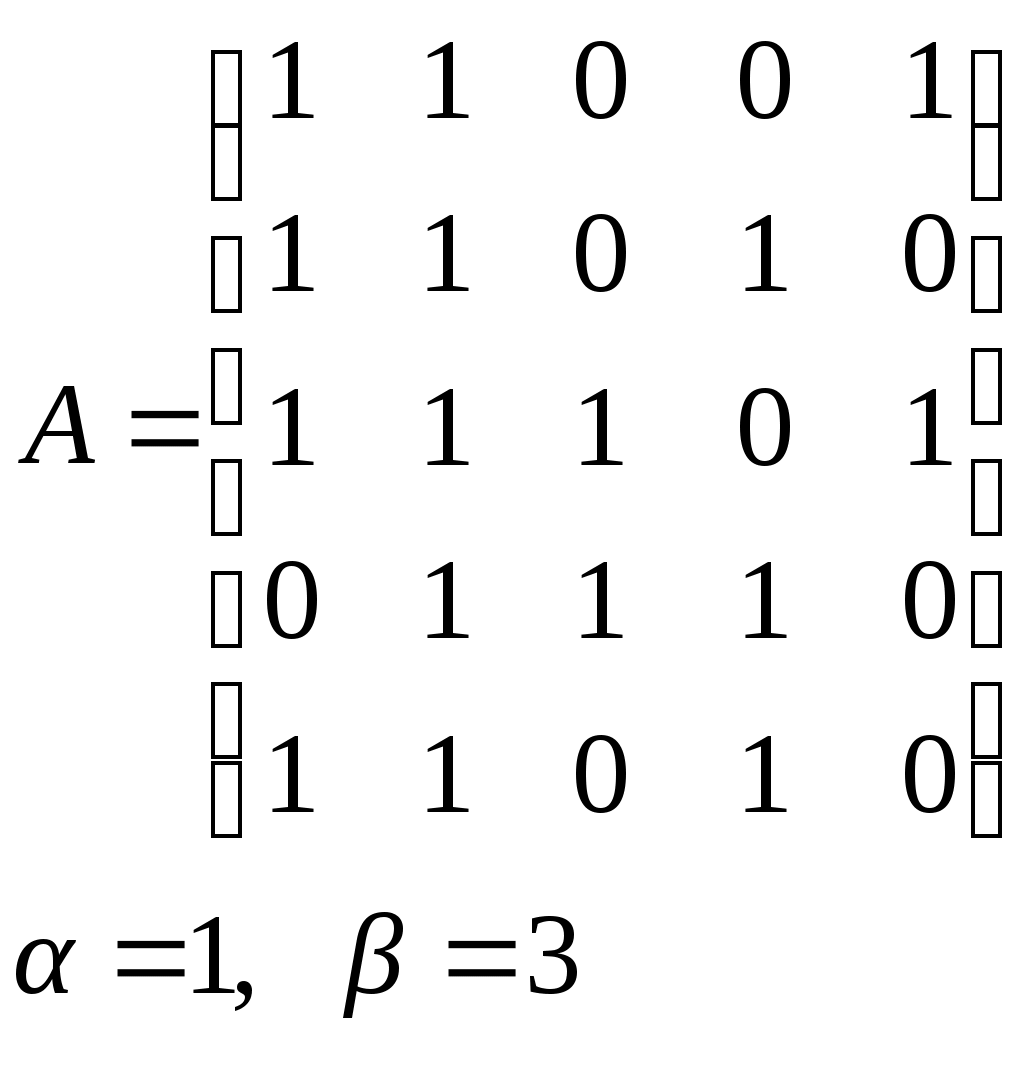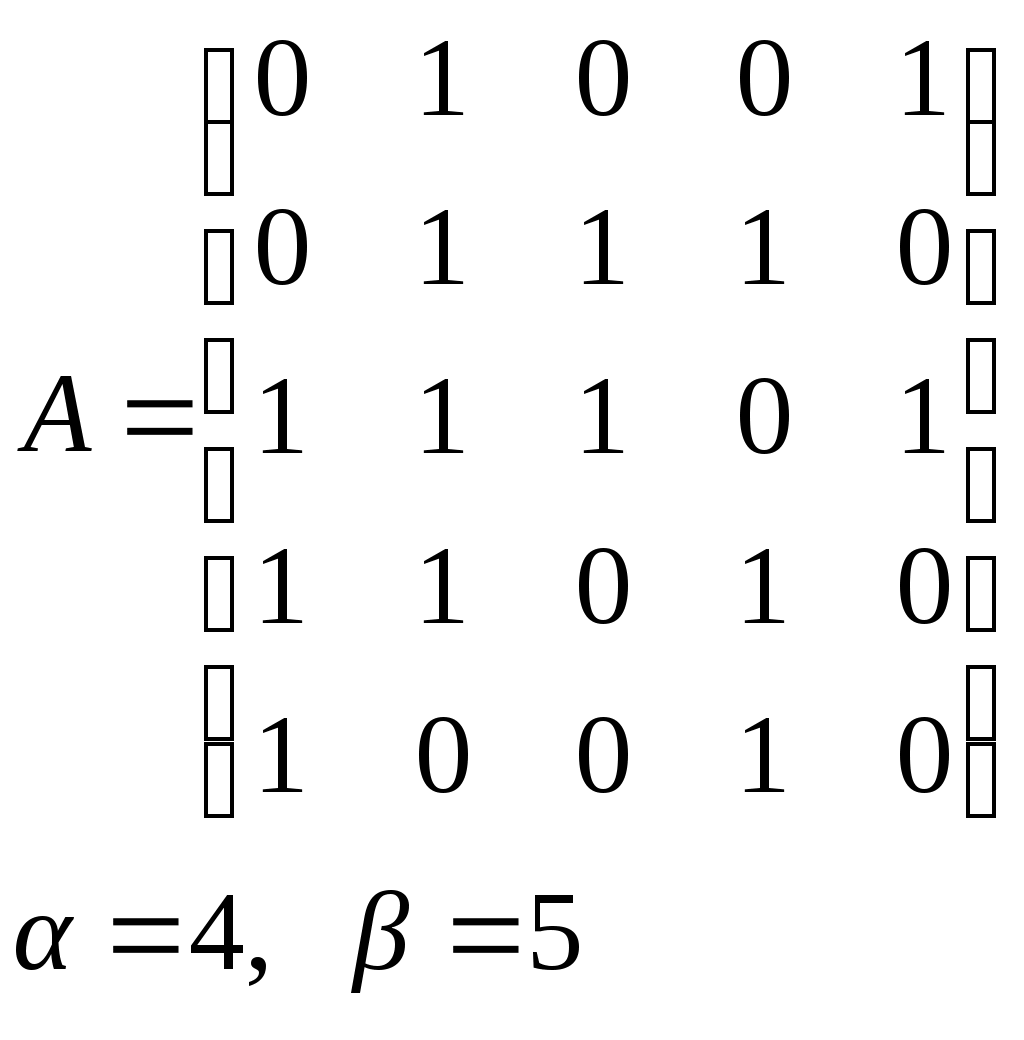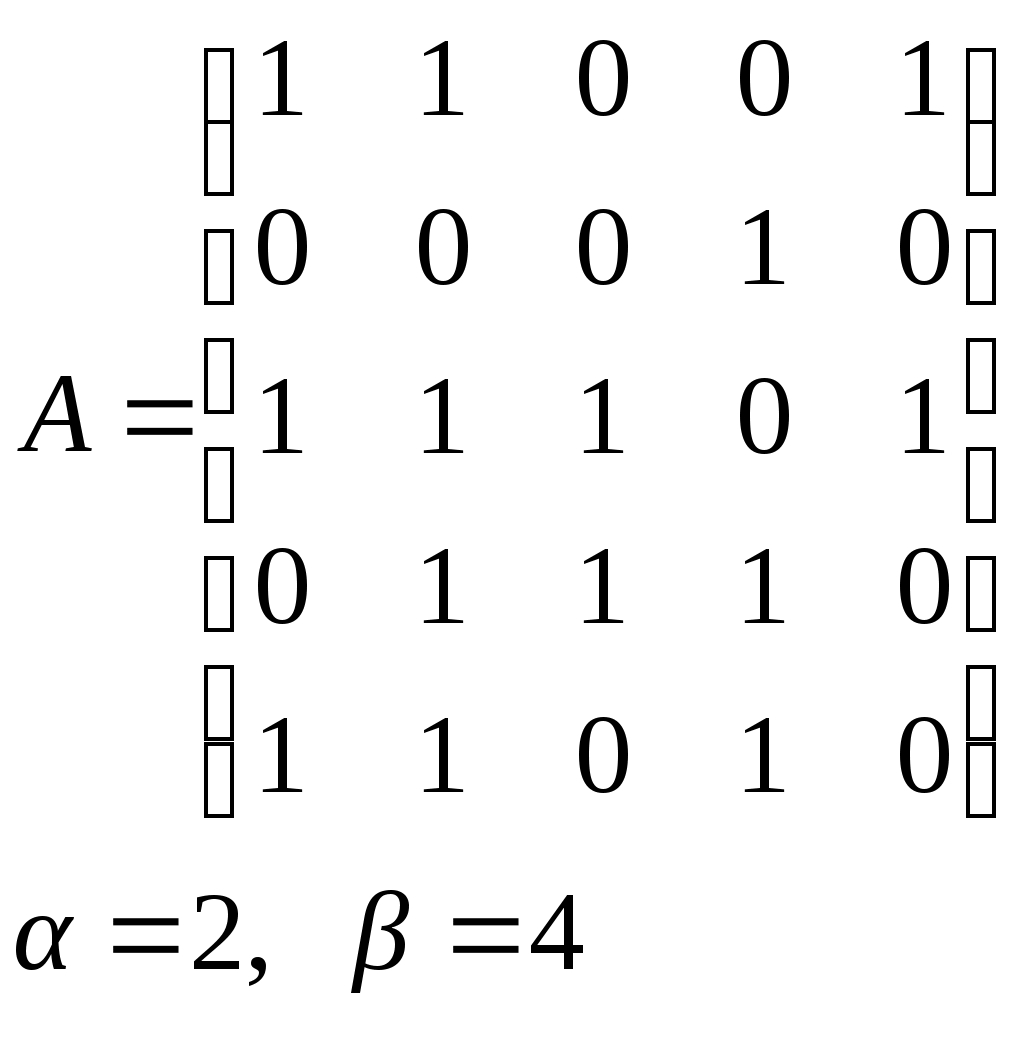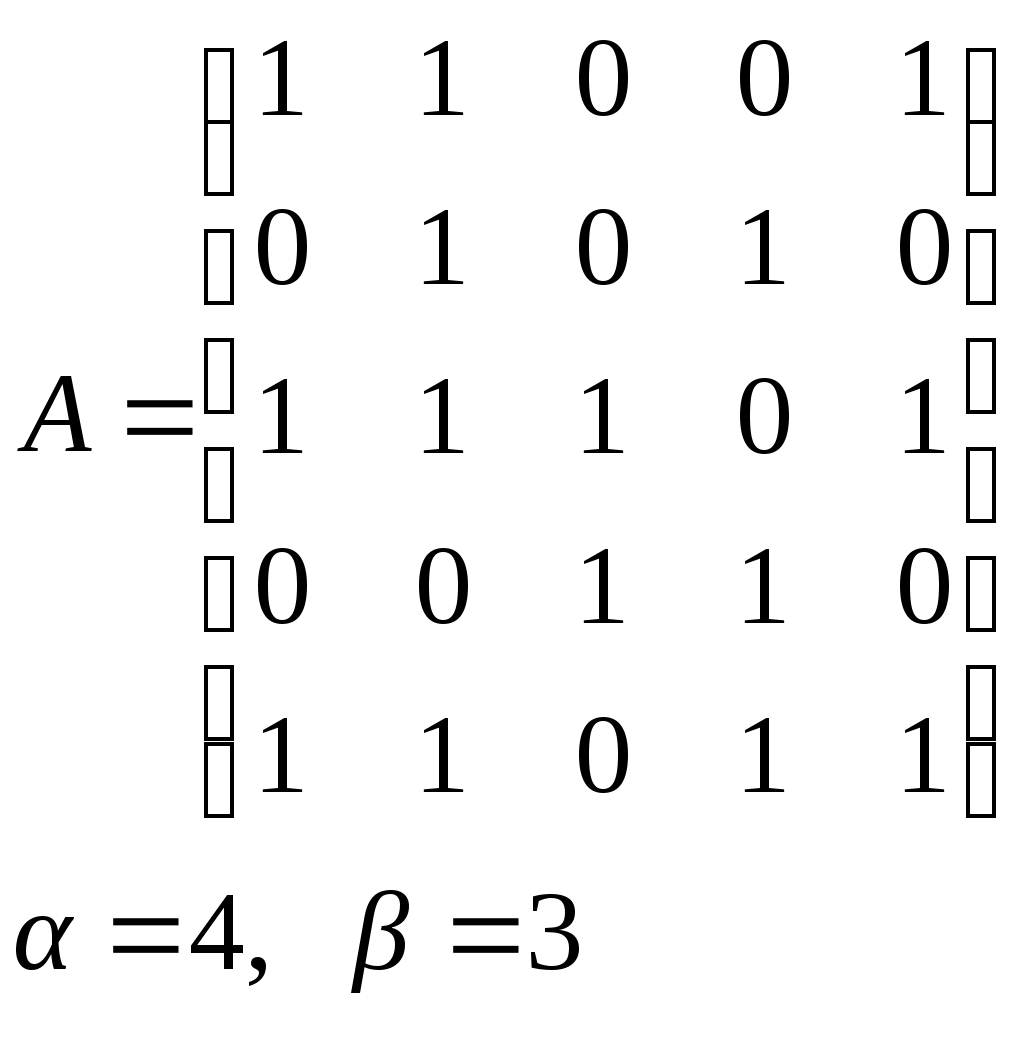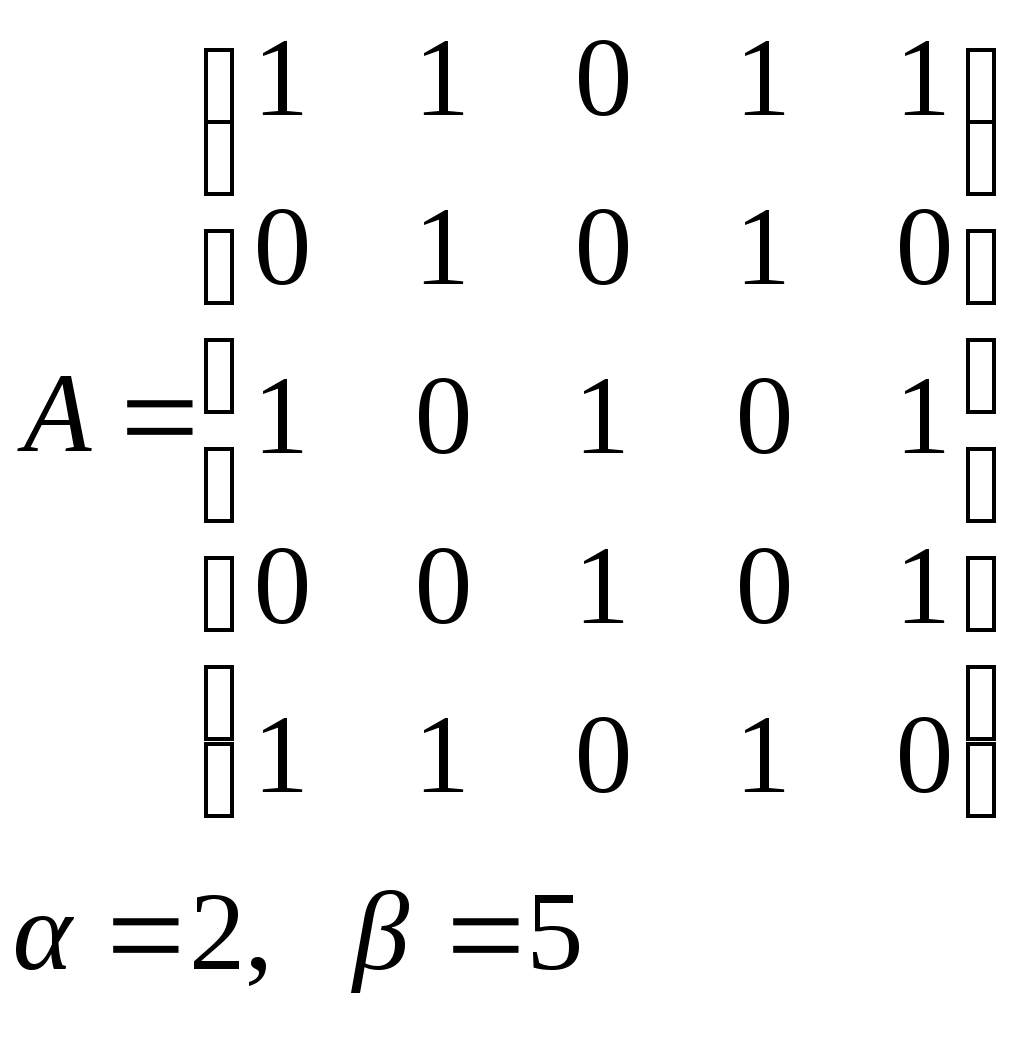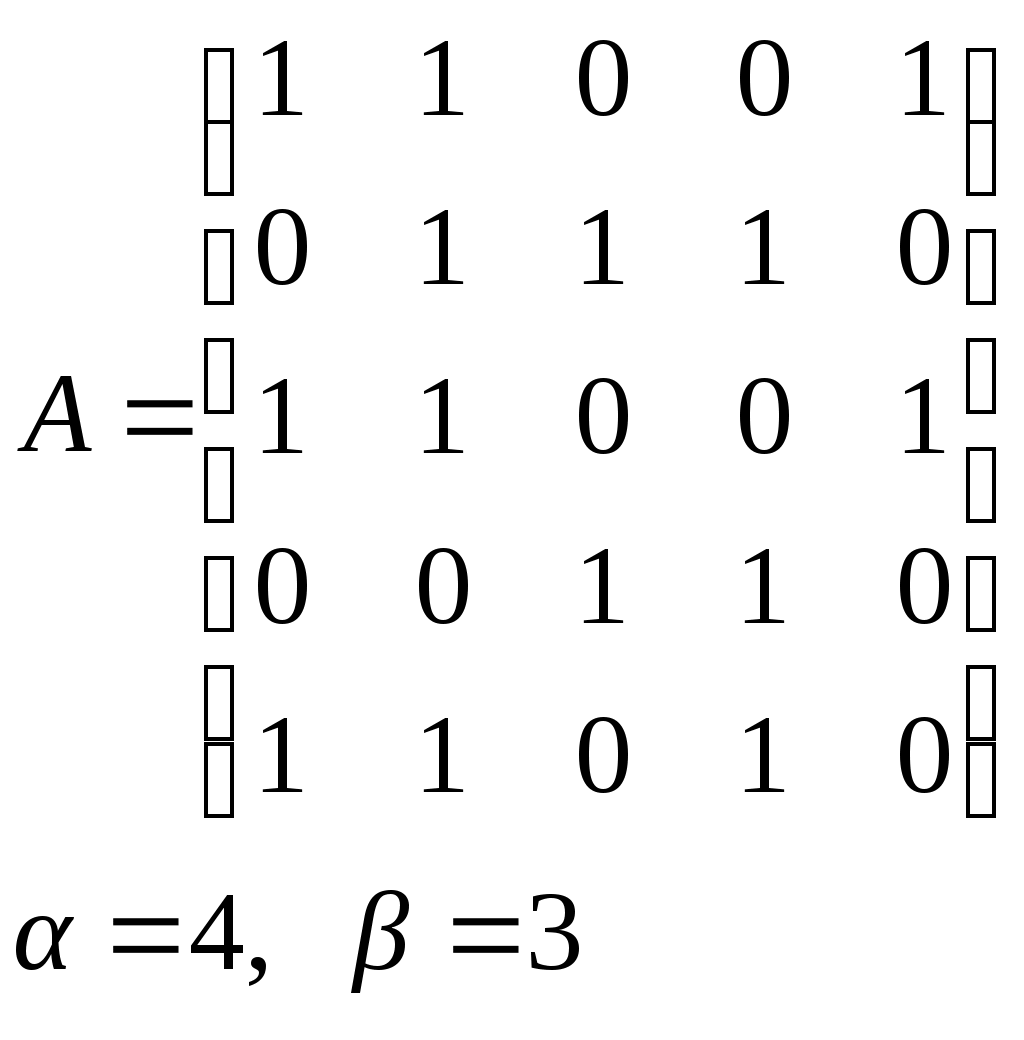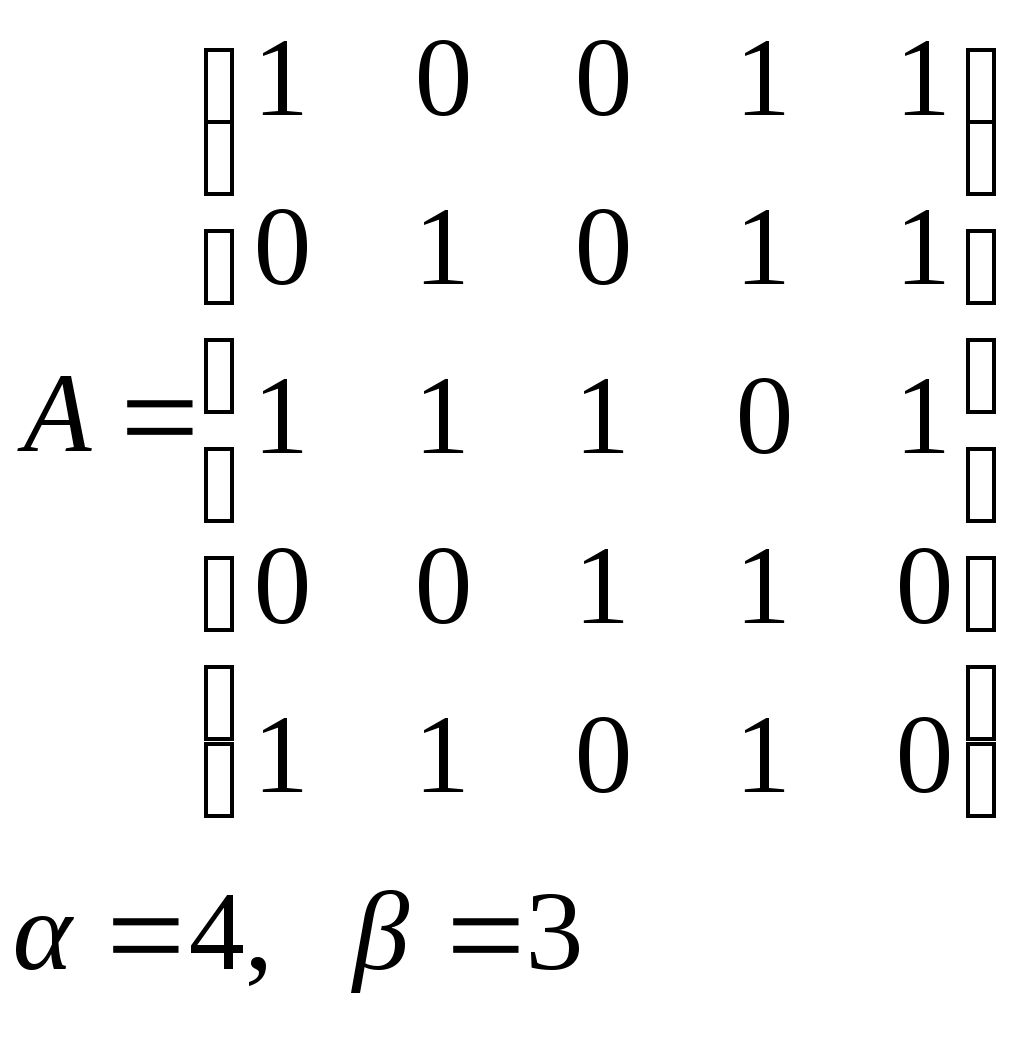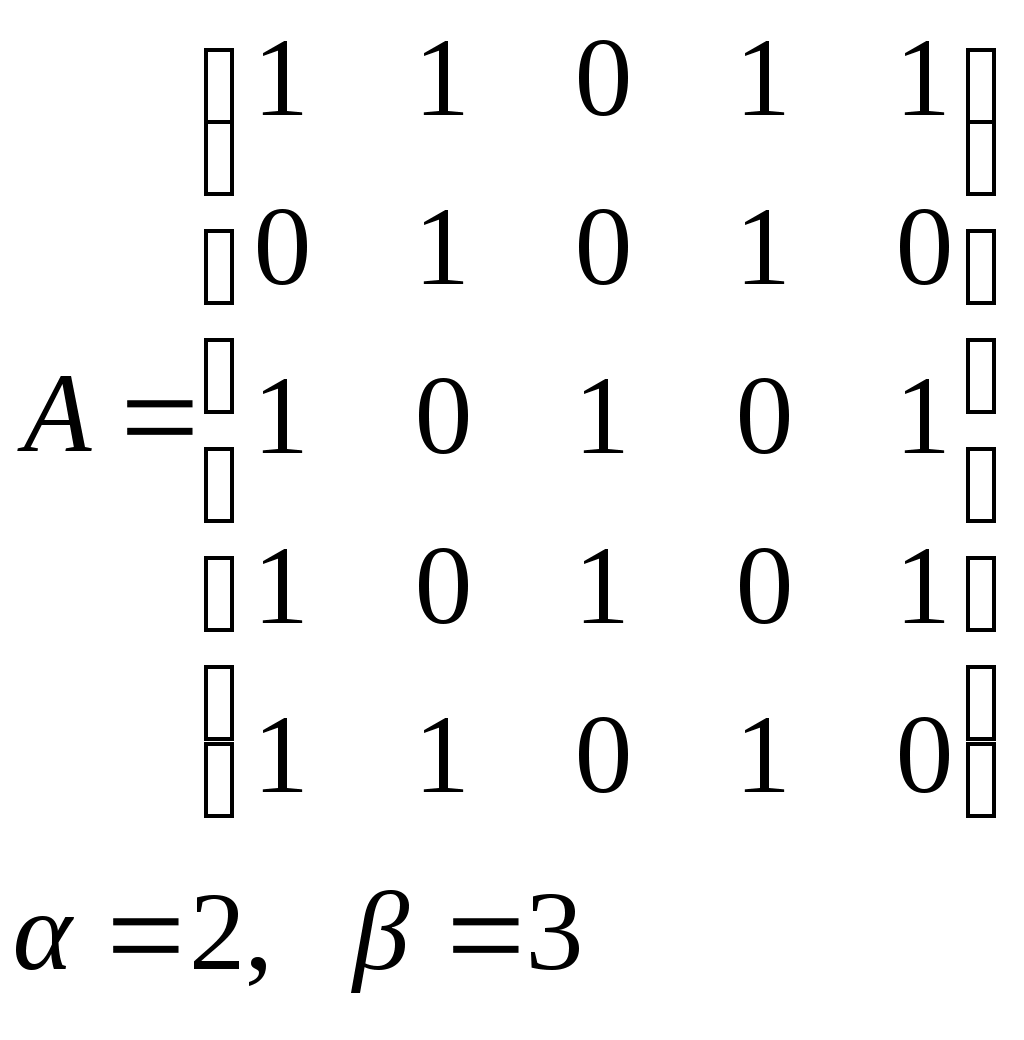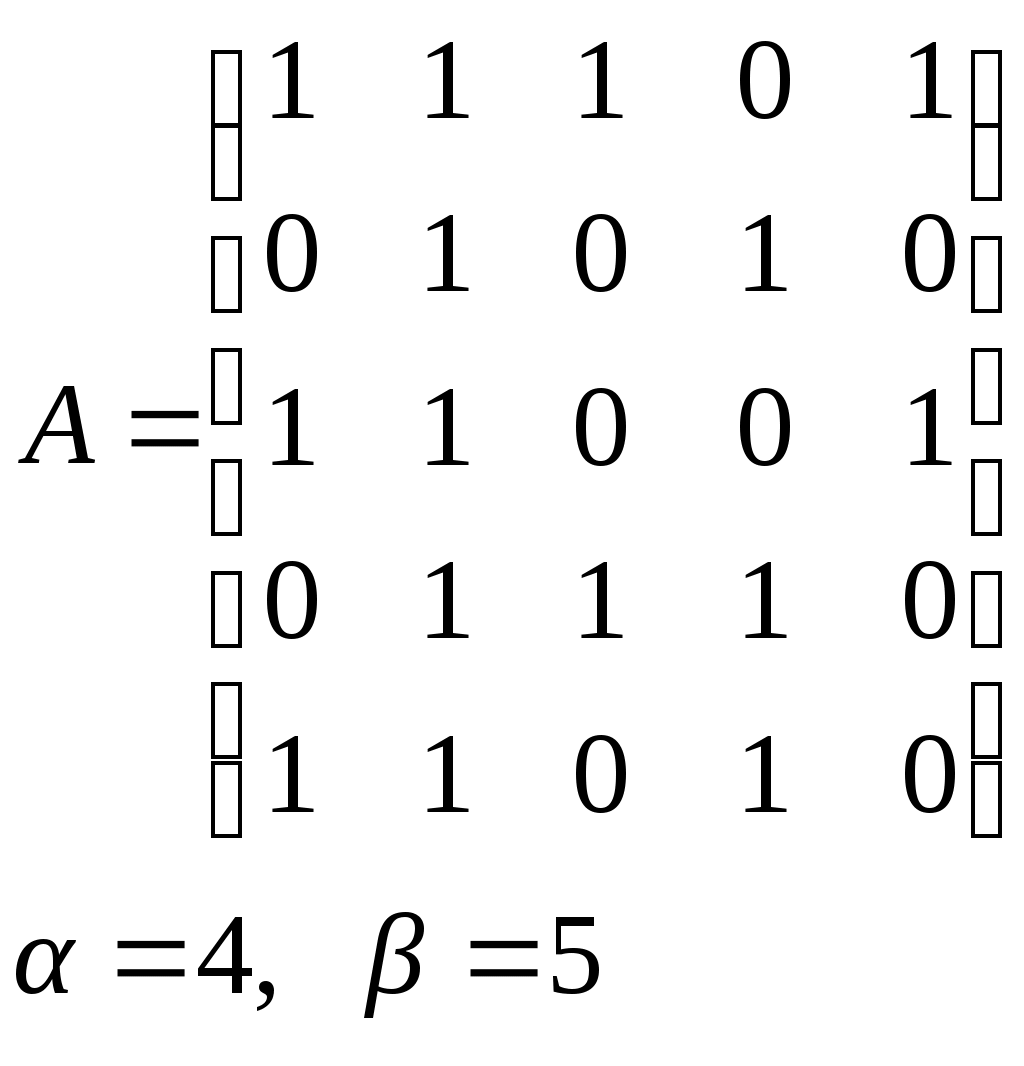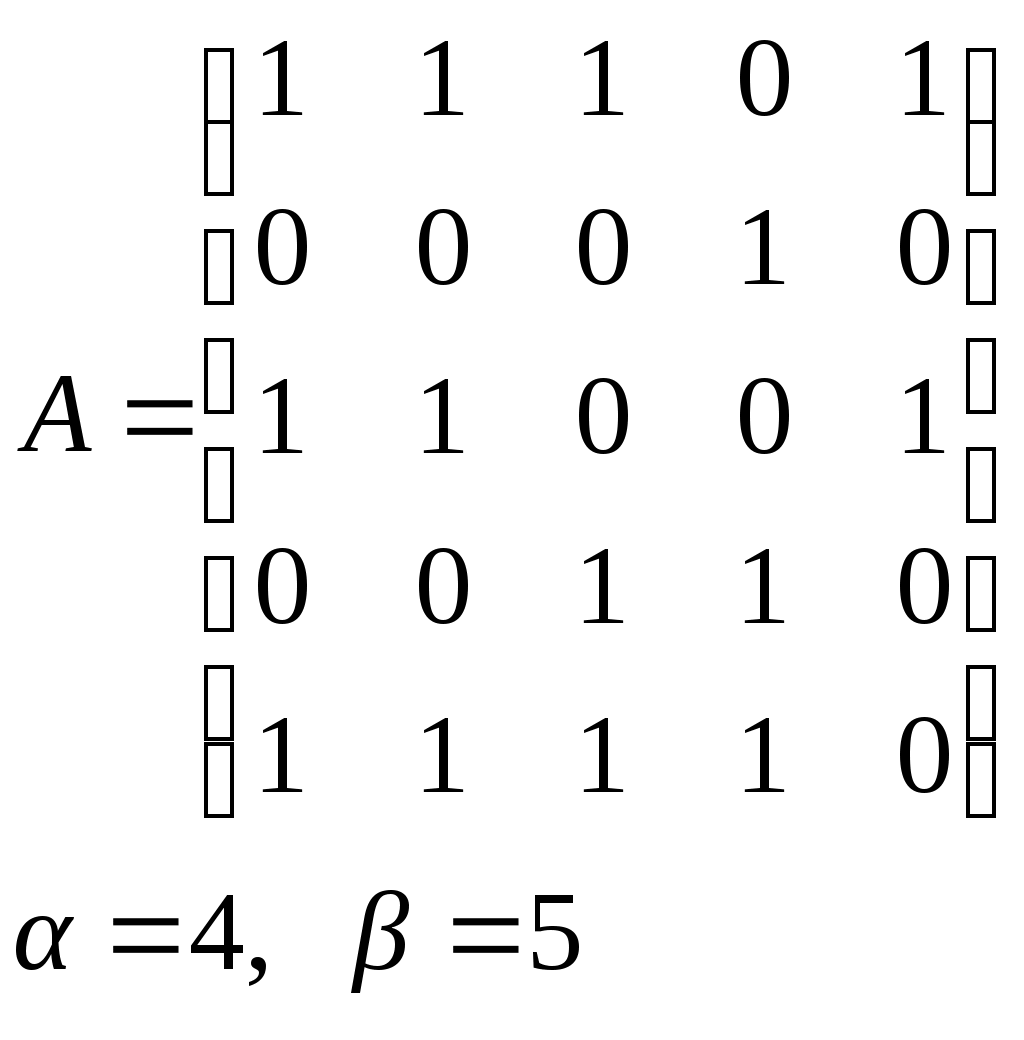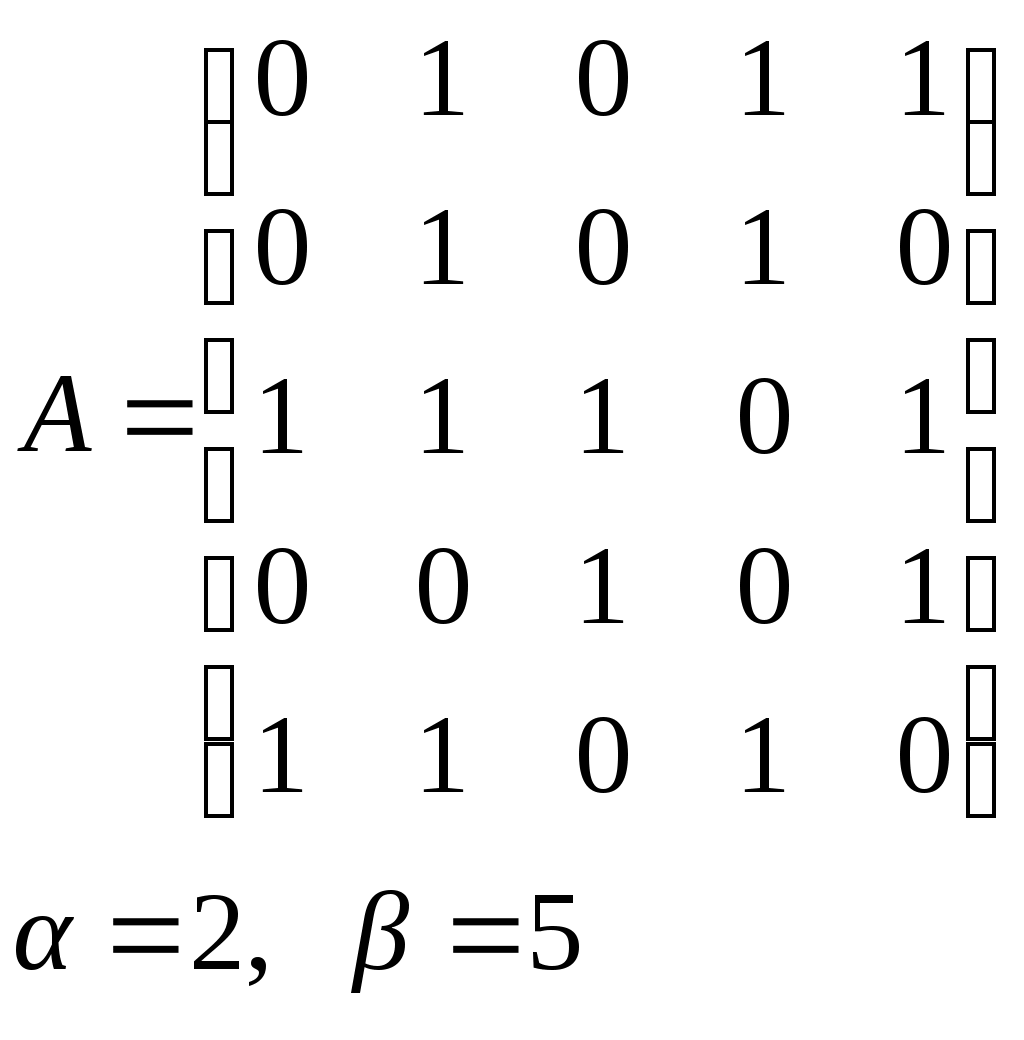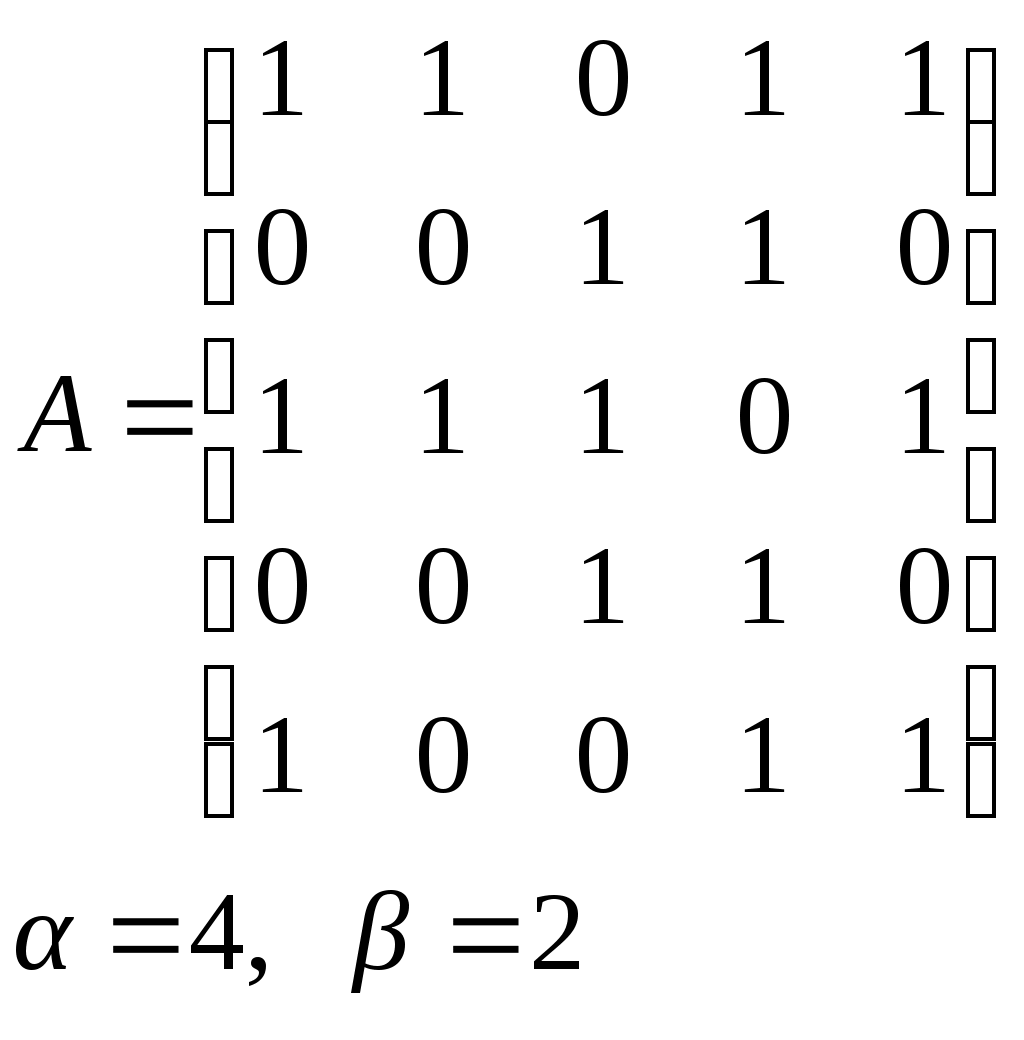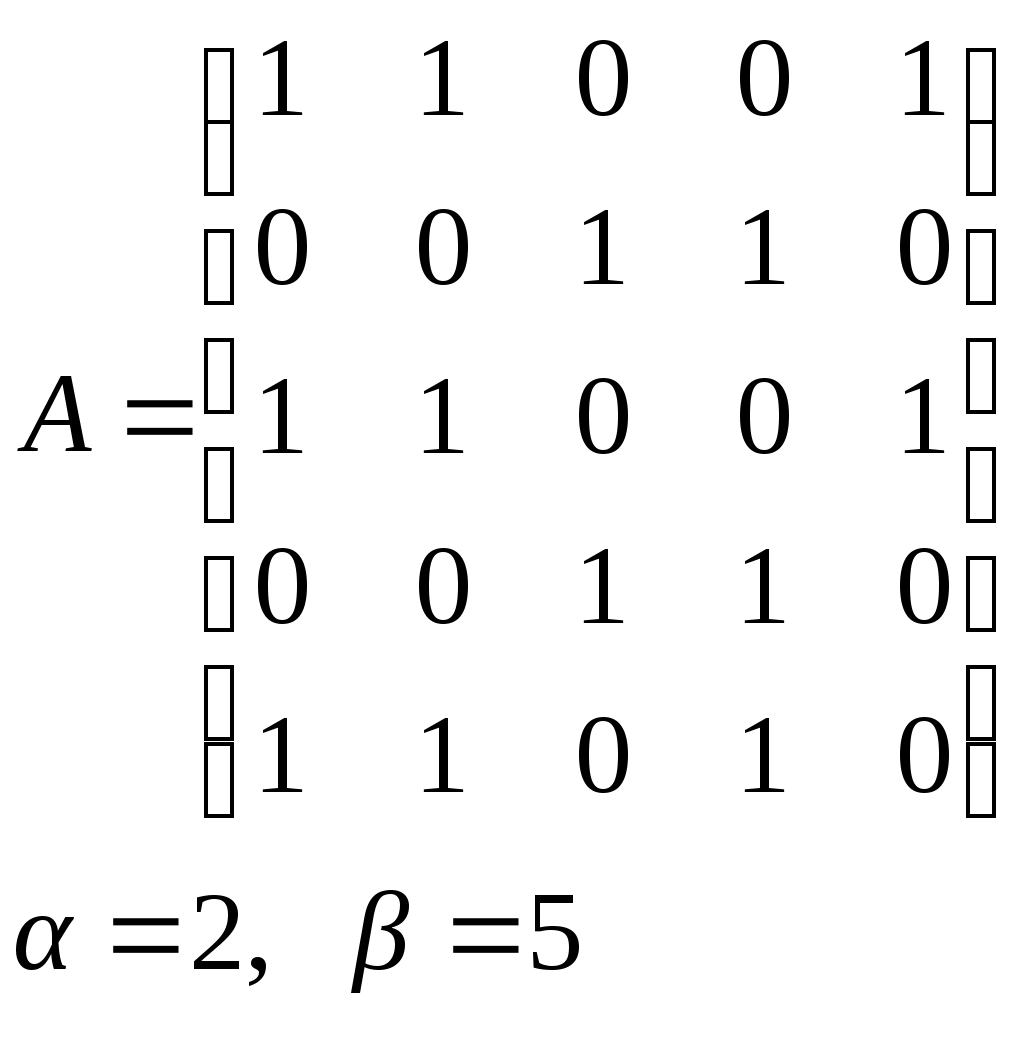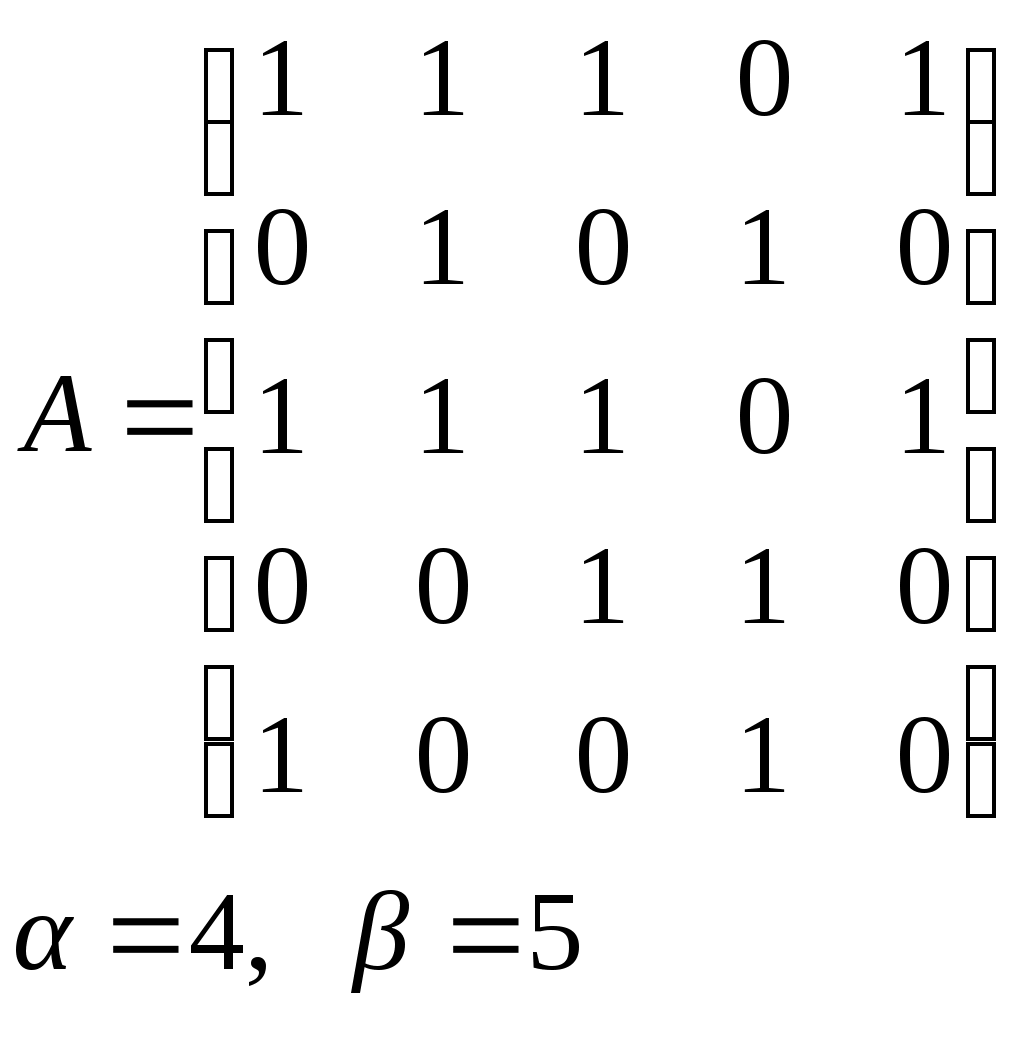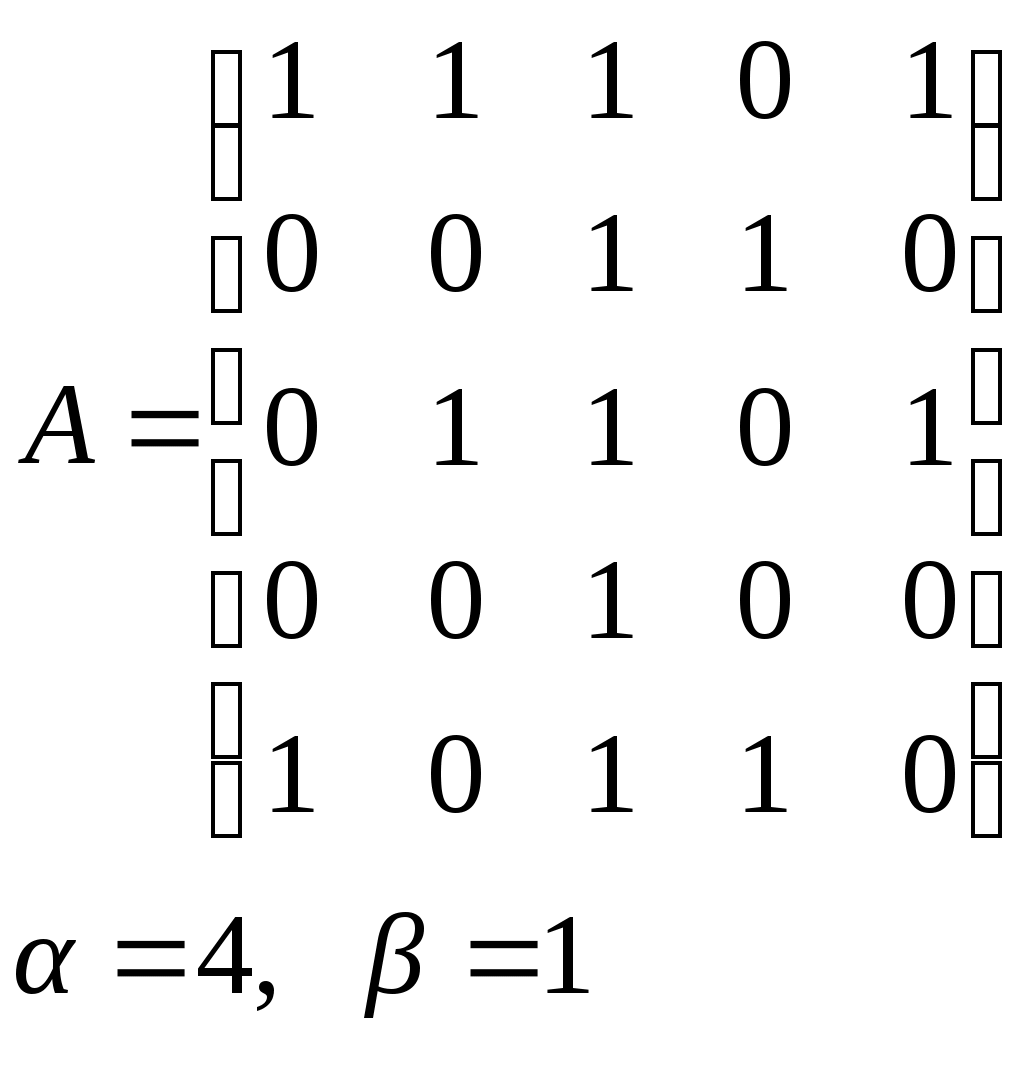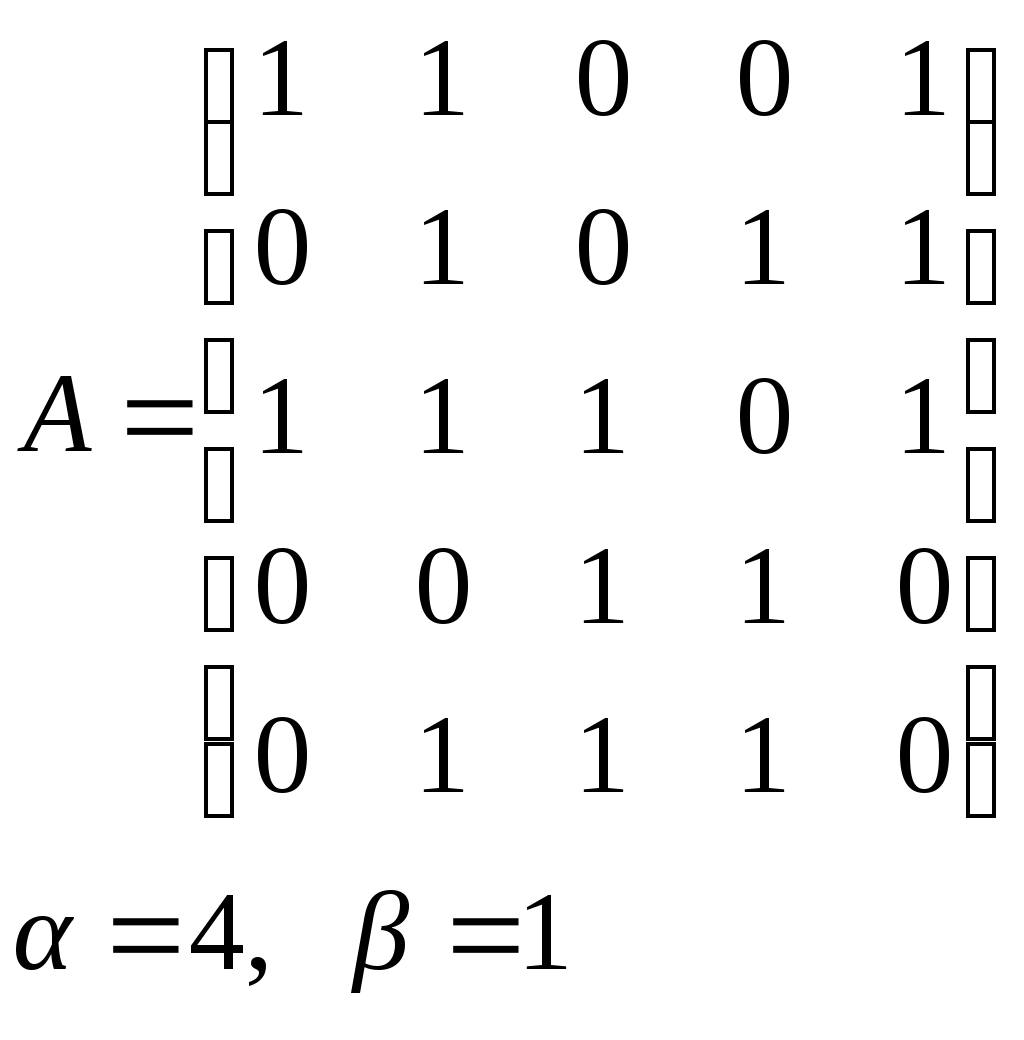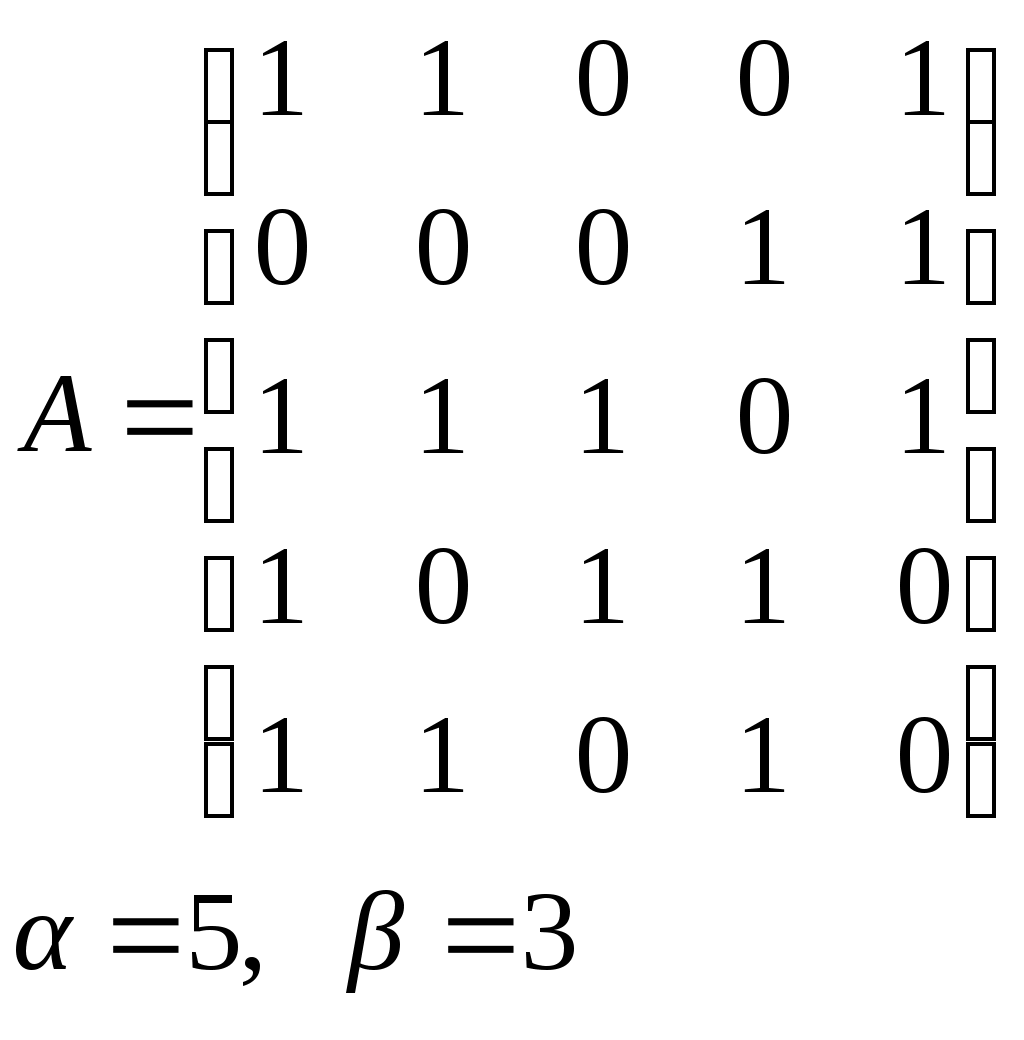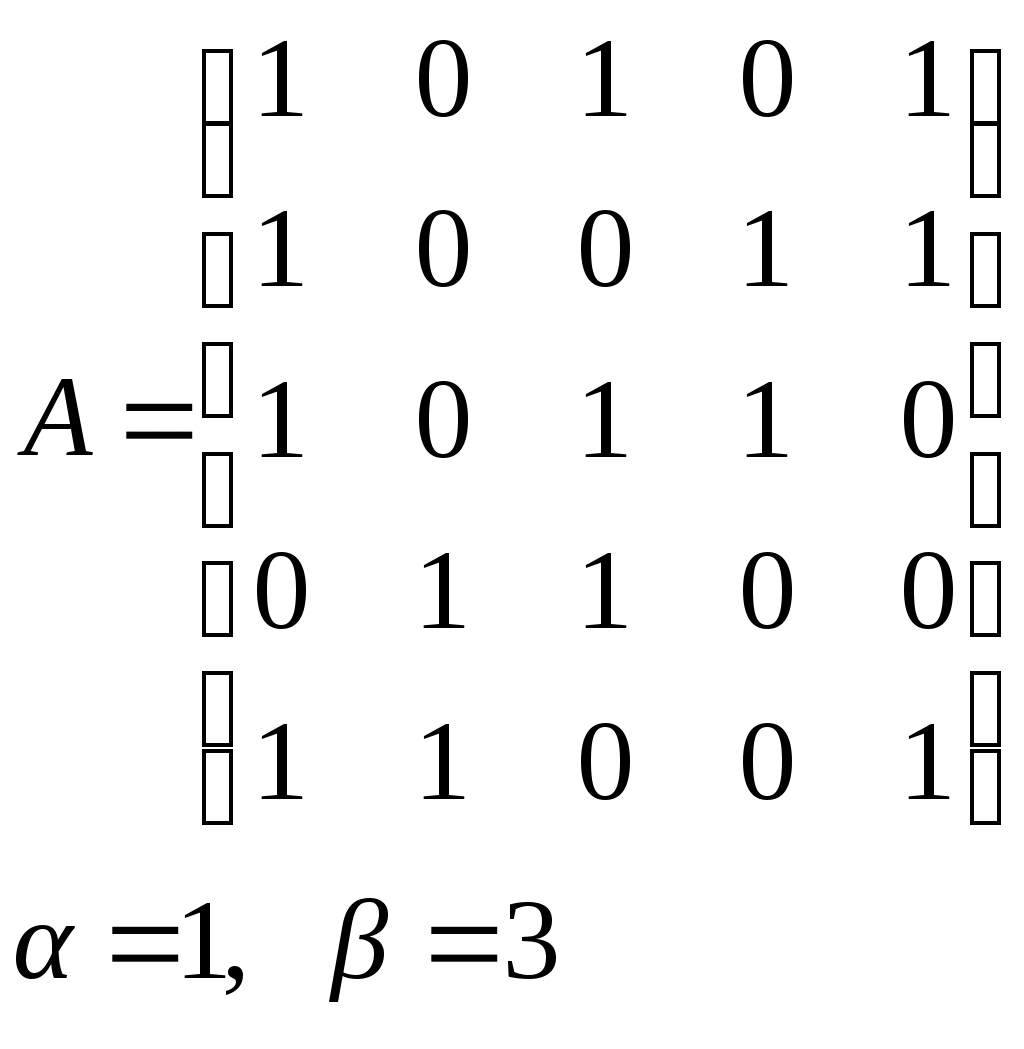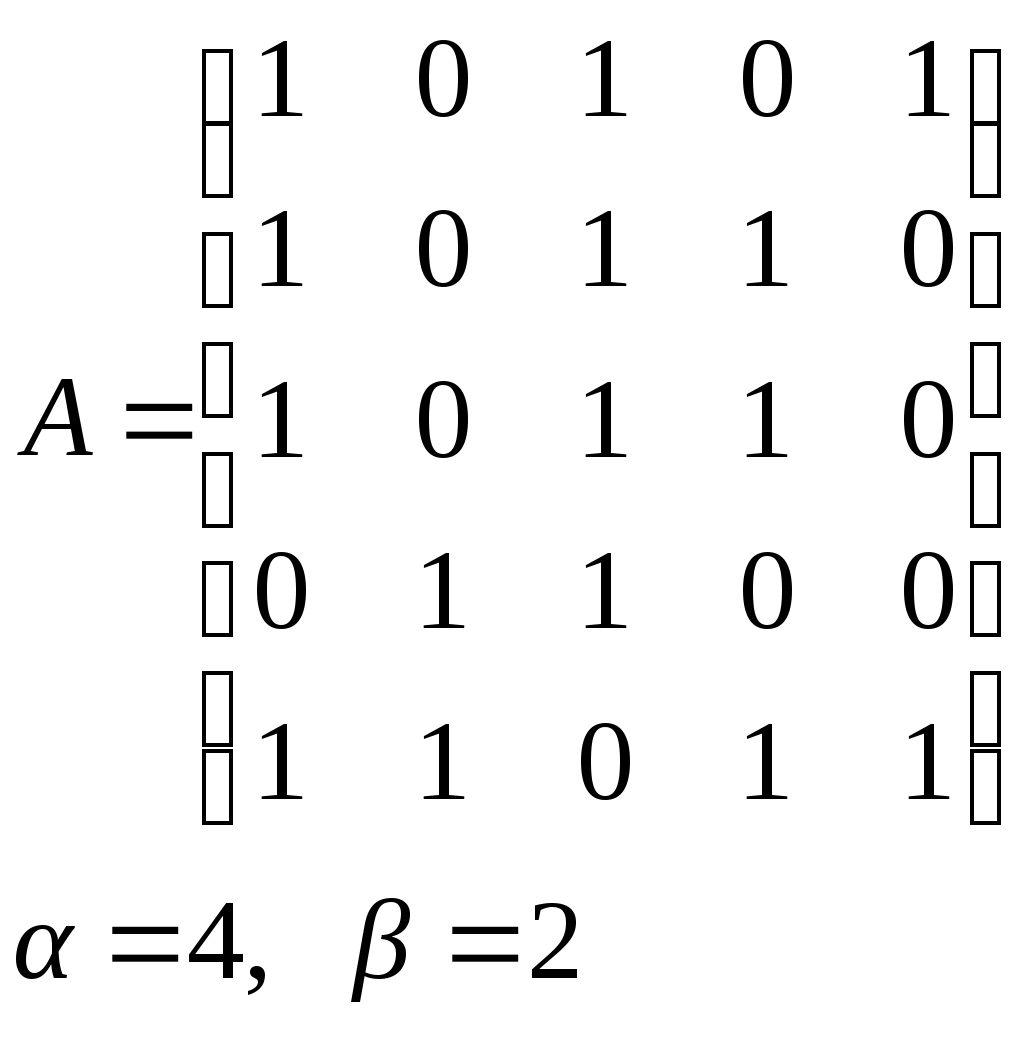Дискретная математика

• Название: Дискретная математика
• Дата: 06.12.2020
• Размер: 0.55 Mb.
• Имя файла: MU_DM_IST (1).doc
• Тип: Методические указания; #157628
• страница: 2 из 3

10. Сколько различных делителей у числа 2520?

11. Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа, которые не содержат одинаковых цифр. Определить количество чисел, в которых цифры 1 и 2 содержатся одновременно.

12. В Стране Чудес построили еще один город – D и несколько дорог – две из A в D и две из D в C. Сколькими способами можно теперь добраться из города A в город C?

13. Сколько диагоналей в выпуклом n – угольнике?

14. Сколько различных делителей имеет число ?

15. Из колоды в 36 карт наудачу без возвращения вынимают по одной карте 3 раза. Сколько существует различных способов получения 3 – х карт, среди которых на первых двух местах – бубна, а на третьем – пика.

16. Автомобильные номера некоторой страны состоят из 3 букв (все буквы различны) и четырех цифр (цифры могут повторяться). Сколько максимально машин может быть в этой стране, если в её алфавите 26 букв?

17. Даны две параллельные прямые. На одной из них имеется 14 точек, а на другой – 20. Сколько существует четырехугольников с вершинами в данных точках?

18. Сколько различных делителей у числа 3640?

19. В классе 15 мальчиков и 15 девочек. Сколькими способами их можно разбить на пары танцевать вальс на концерте?

20. Из колоды в 36 карт наудачу берут 6 карт. Сколькими способами можно взять 6 карт так, чтобы среди них был хотя бы один туз?

21. На полке стоит 12 книг. Сколькими способами можно выбрать из них 5 книг, никакие две из которых не стоят рядом?

22. За пересылку бандероли надо уплатить 18 рублей. Сколькими способами можно оплатить пересылку марками достоинством в 4, 6 и 10 рублей, если два способа, отличающиеся порядком марок, считаются различными (марки наклеиваются в один ряд).

23. На окружности взята 101 синяя и одна красная точка. Сколько существует вписанных в окружность выпуклых многоугольников, одна вершина которых красная, а остальные синие?

24. Сколько различных делителей у числа 2420?

25. Сколькими способами можно выбрать из натуральных чисел от 1 до 30 три числа так, чтобы их сумма была четной?

26. Сколько различных трехзначных чисел, делящихся на 4 можно составить из цифр 1, 2, 3, 4, 5, 6, 7, при условии, что цифры в числе не повторяются?
ЗАДАНИЕ 3

Восстановить орграф по матрице смежности. Записать для полученного орграфа одну из матриц инцидентности, пронумеровав произвольно дуги, и найти количество путей длины 3 из вершины в вершину . Указать эти пути, если они существуют.

Вариант №	Матрица смежности	Вариант №	Матрица смежности
1		14
2		15
3		16
4		17
5		18
6		19
7		20
8		21
9		22
10		23
11		24
12		25
13		26

ЗАДАНИЕ 4

Дано число 800+5n+7k–23r, где n – число букв фамилии, k – номер варианта, r – число букв полного имени.

а) Восстановить граф, считая это число кодом Харари.

б) Проверить, является ли нумерация вершин канонической, то есть, является ли это число действительно кодом Харари?
ЗАДАНИЕ 5

Восстановить дерево по заданному коду Прюфера.

Вариант'>Вариант	Код	Вариант	Код
1	{3,2,1,4,1,2,3,4,7}	14	{3,2,1,4,1,2,8,1,5}
2	{2,2,1,4,1,2,3,3,8}	15	{3,1,1,4,1,2,3,2,4}
3	{1,2,1,4,1,2,3,4,6}	16	{3,4,1,4,1,2,3,7,6}
4	{4,2,1,4,1,2,3,5,5}	17	{3,5,1,4,1,2,3,2,4}
5	{5,2,1,4,1,2,3,7,2}	18	{3,6,1,4,1,2,3,4,7}
6	{6,2,1,4,1,2,3,6,4}	19	{3,7,1,4,1,2,3,5,9}
7	{7,2,1,4,1,2,3,1,1}	20	{3,8,1,4,1,2,3,2,5}
8	{8,2,1,4,1,2,3,2,7}	21	{3,2,3,4,1,2,3,5,7}
9	{3,2,1,4,1,2,2,4,4}	22	{3,2,2,4,1,2,3,4,4}
10	{3,2,1,4,1,2,1,3,3}	23	{3,2,4,4,1,2,3,3,8}
11	{3,2,1,4,1,2,4,5,8}	24	{3,2,5,4,1,2,3,7,6}
12	{3,2,1,4,1,2,5,6,2}	25	{3,2,6,4,1,2,3,8,8}
13	{3,2,1,4,1,2,6,1,8}	26	{3,2,7,4,1,2,3,1,1}

ЗАДАНИЕ 6

Данную формулу преобразовать к виду:

а) СДНФ с помощью алгоритма;

б) СКНФ с помощью двойственности;

в) многочлена Жегалкина.

В пунктах а) и б) ответ проверить с помощью таблицы истинности.

Вариант	f