Дискретная математика
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
3. ПРИМЕР ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ ПО ТЕМЕ «ОСНОВЫ ТЕОРИИ МНОЖЕСТВ И КОМБИНАТОРИКИ» 1. Рассмотрим отображение f: RR, заданное формулой f(x)= cos4x + 6 . Является ли оно биективным отображением? 2. Даны множества A={-2, 0, 3, а}, B{0,1,2,3, а, б}. Найдите множества 3. Сколько различных пятизначных нечетных чисел можно составить из цифр 0, 2, 4, 5, 6, 7, 9 при условии, что цифры в числе не повторяются? 4. На олимпиаде по дискретной математике распределяется три призовых места. Сколькими способами это можно сделать при условии, что в олимпиаде участвовало 25 человек? 5. На карточках написаны буквы Б, А, Р, А, Б, А, Н. Сколько различных семибуквенных наборов из них можно составить? 6. На множестве людей рассмотрим отношение «быть одной группы крови». Является ли оно отношением эквивалентности? Что является классом эквивалентности? 4. ПРИМЕР ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ ПО ТЕМЕ «ГРАФЫ КАК СТРУКТУРА ОБРАБОТКИ ДАННЫХ» Восстановить граф по матрице смежности 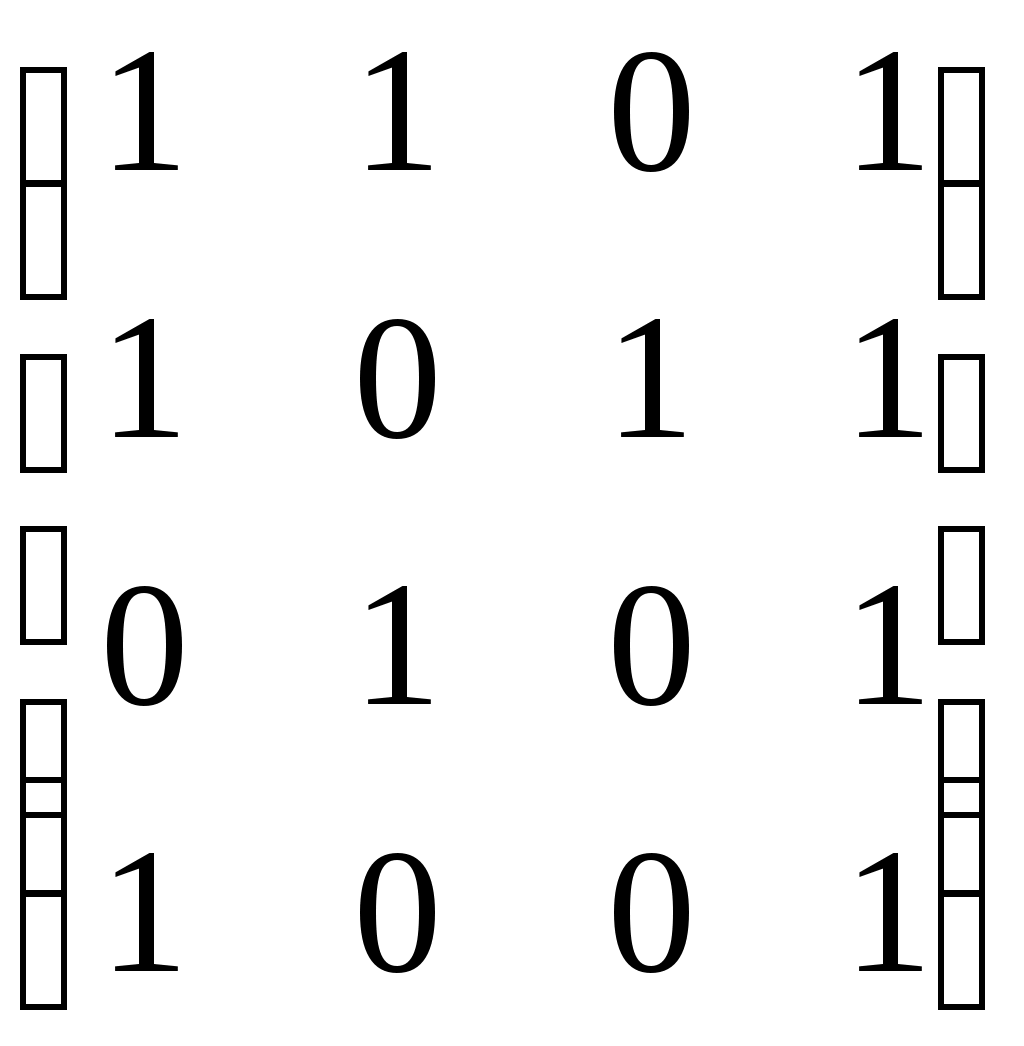 Восстановить граф по матрице инцидентности 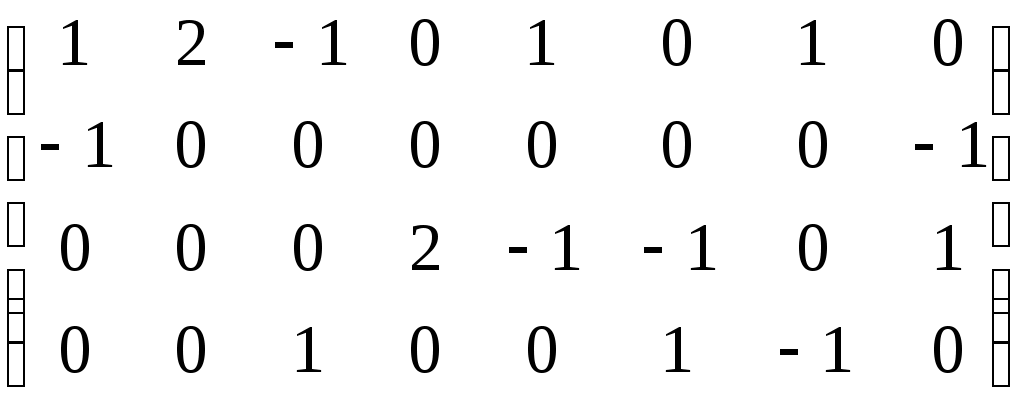 По матрице смежности 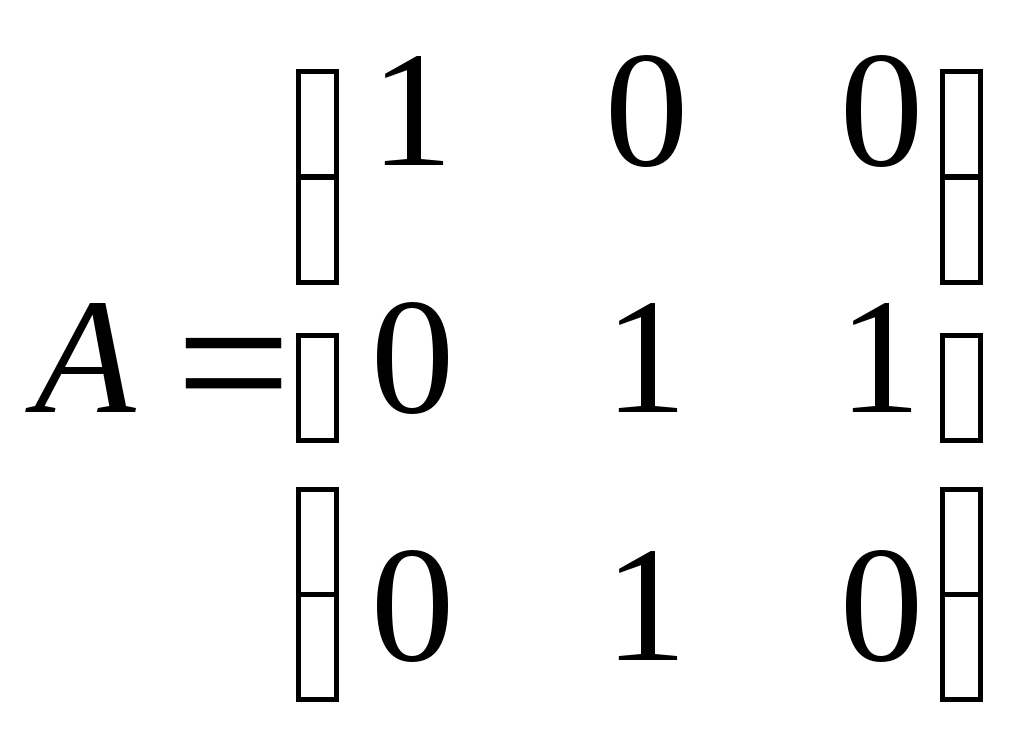 восстановить граф. восстановить граф.Найти число путей длины 3 из первой вершины в третью. Перечислить эти пути. Восстановить дерево по коду Прюфера {3,2,1,4,1,2,3}. Найти СДНФ булевой функции Ответ проверить по таблице истинности. 5. ВОПРОСЫ К ЭКЗАМЕНУ 1. Что называется объединением, пересечением, разностью, симметрической разностью множеств, дополнением множества? 2. Что такое инъективное, сюръективное, биективное отображение (с примерами)? 3. Что такое мощность множества двоичных наборов и мощность множества всех подмножеств данного множества? 4. Что такое правило произведения (с примером)? 5. Что такое перестановки и чему равно число всех перестановок (с примером)? 6. Что такое размещения и чему равно число всех размещений (с примером)? 7. Что такое сочетания и чему равно число всех сочетаний (с примером)? 8. Что такое перестановки с повторениями и чему равно число всех перестановок с повторениями (с примером)? 9. Что такое рефлексивное, симметричное, транзитивное отношение, отношение эквивалентности и каково его основное свойство? 10. Что такое отношение нестрогого порядка, строгого порядка? 11. В чем состоит числовое сравнение двоичных наборов и как сравнить двоичные наборы по Парето? 12. Что такое орграф, граф, вершина, дуга, ребро, путь, цепь, контур, цикл? 13. Каков алгоритм решения задачи о кратчайшем пути в невзвешенном графе? 14. Каков алгоритм решения задачи о кратчайшем пути во взвешенном графе? 15. Что такое эйлерова цепь (цикл), у каких графов они существуют? 16. В чем состоит формула Эйлера и для каких объектов она верна? 17. Как выглядят непланарные графы № 1 и № 2, типов 1 и 2 и в чем состоит теорема Куратовского-Понтрягина? 18. Что такое хроматическое число графа и какова его величина? 19. Что такое хроматический индекс графа и какова его величина? 20. Что такое матрица смежности орграфа и каким свойством обладает матрица смежности неориентированного графа? 21. Что такое матрица инцидентности орграфа? Как по матрице инцидентности восстановить граф? 22. Как строится код Харари? 23. Что называется деревом, ордеревом и как они связаны между собой? 24. Как строится префиксный код бинарного ордерева? 25. Как строится код Прюфера? 26. Назовите три способа обхода бинарного ордерева (с примером)? 27. Что называется атомом, списком и как связаны деревья со списками? 28. Определение булевой функции. Как выглядят таблицы истинности для восьми важнейших булевых функций? 29. Как выразить дополнительные логические операции через три основные: дизъюнкцию, конъюнкцию и отрицание? 30. Что такое ЭК, ДНФ, правильная ЭК, полная ЭК, СДНФ? 31. Как получить СДНФ с помощью таблицы истинности? 32. Каковы основные шаги преобразования формулы в СДНФ? 33. Что такое двойственная булева функция, самодвойственная булева функция, закон двойственности? 34. Как получить СКНФ, используя двойственность? 35. Как получить СКНФ, используя таблицу истинности? 36. Что такое многочлен Жегалкина? Представление булевой функции в виде многочлена Жегалкина. 37. Что такое монотонная булева функция и как это связано с дизъюнкцией и конъюнкцией? 38. Что такое линейная функция, функция, сохраняющая ноль и функция, сохраняющая единицу? 39. В чём состоит теорема Поста? Как практически применить теорему Поста? 40. Понятие абстрактного алфавита и кода, примеры. 41. Двоичные коды. 42. Коды с обнаружением и исправлением ошибок. 43. Коды Хемминга. Построение кодера и декодера (7,4) – кода Хемминга. 44. Коды, исправляющие несколько ошибок. 6. ТЕМАТИКА ЭКЗАМЕНАЦИОННЫХ ЗАДАЧ Множества. Операции над множествами. Отображение множеств. Мощность множества. Основы комбинаторики. Правило произведения. Отношения на множестве. Основные понятия теории графов: ориентированные и неориентированные графы. Пути, маршруты, циклы, связность графов. Задача о кратчайшем пути в графе. Задача Эйлера. Плоские, планарные и непланарные графы Формула Эйлера. Раскраска графа. Хроматическое число и хроматический индекс графа. Матрица смежности. Матрица инцидентности. Код Харари. Деревья и ордеревья. Префиксный код бинарного ордерева. Код Прюфера для деревьев и ордеревьев. Обход дерева. Понятие списка. Деревья и списки. Деревья и арифметические выражения. Коды Хемминга. Булевы функции. Основные логические операции. Построение СДНФ булевой функции. Двойственные булевы функции. Построение СКНФ булевой функции. Основные свойства булевых функций. Функциональная полнота системы булевых функций. Теорема Поста. 7. ПРИМЕРЫ ЭКЗАМЕНАЦИОННЫХ ЗАДАЧ Проиллюстрировать диаграммой Эйлера – Венна формулы: (А∩В) C=(A C) ∩(B C); A\(B C)=(A\B) ∩ (A\C) Доказать методом «включений» формулу (A B) ∩ C=(A∩C) (B∩C) Рассмотрим отображение f:R→R, заданные формулой, f(x)=x3-4x4 ; f(x)=3cos5x ; Является ли оно инъективным, сюръективным, биективным? Даны множества А=(-2;3]; В[-1;5] ; С={4;6} Найти А В; А∩С; В\С; А Δ С; А\В. У ребёнка есть кубики с буквами а,а,а,с,с,у,у,у,у,т,т,т,т,т. Он пытается из них сложить 14-ти буквенное слово. Сколькими способами это можно сделать? В студенческой группе 5 юношей и 15 девушек. Путем жеребьёвки для дежурства выбирается 1 юноша и 2 девушки. Сколькими способами это можно сделать? На студенческой олимпиаде по математике распределяются 1,2,3 места. Пришло поучаствовать 40 студентов. Сколькими способам могут быть распределены призовые места? На множестве людей рассмотрим отношение «жить в одном доме». Является ли оно отношением эквивалентности? На какие классы эквивалентности оно разбивает всё множество людей? На плоскости хОу рассмотрим отношение Г: (х1,у1)Г(х2,у2), если выполнено х1 Найти кратчайший путь из А в В в графе     В ВА 11. Восстановить орграф по матрице смежности 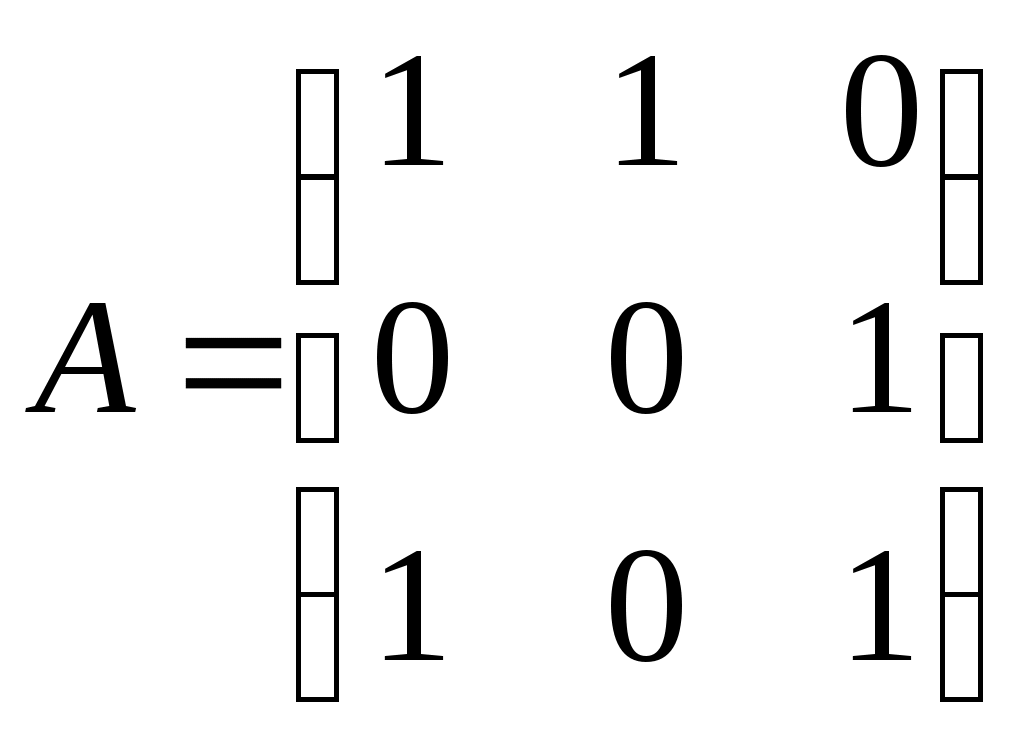 Найти кратчайший путь из А в В во взвешенном графе 6 5 1 2 2 3 1 4          4 3 В 4 3 В    3 9  А 1 5 А 1 52   9  О           бладают ли эйлеровой цепью графы бладают ли эйлеровой цепью графы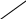  Восстановить граф по матрице смежности 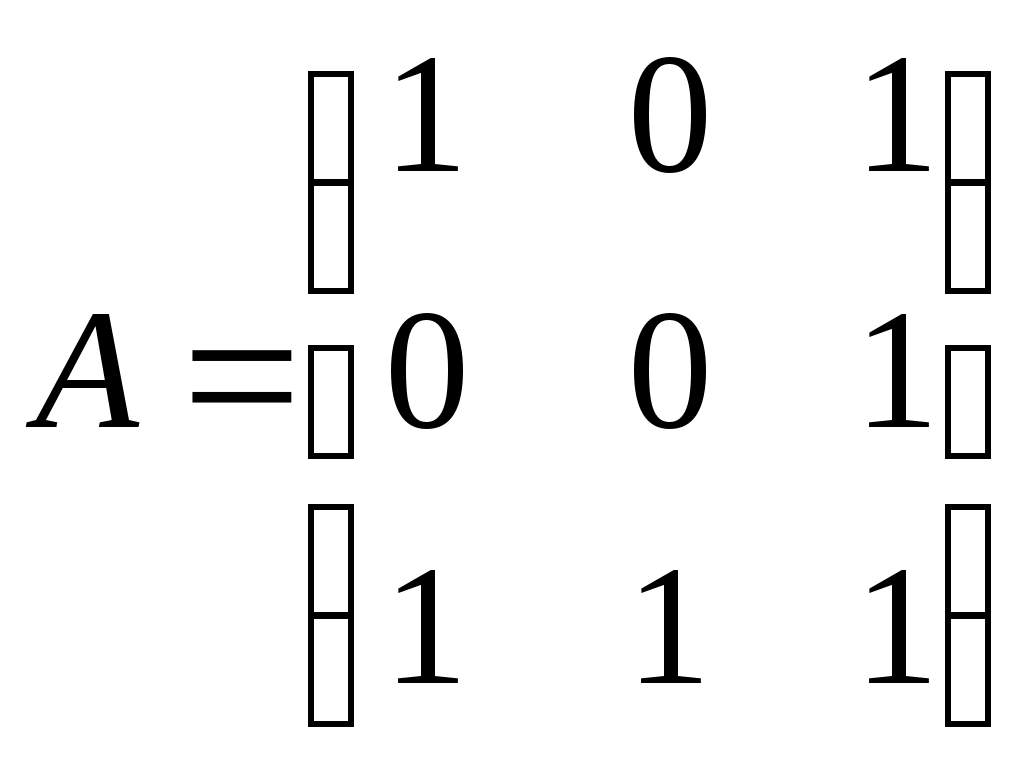 Сколько путей длины три из первой вершины в третью существует у графа, заданного матрицей смежности 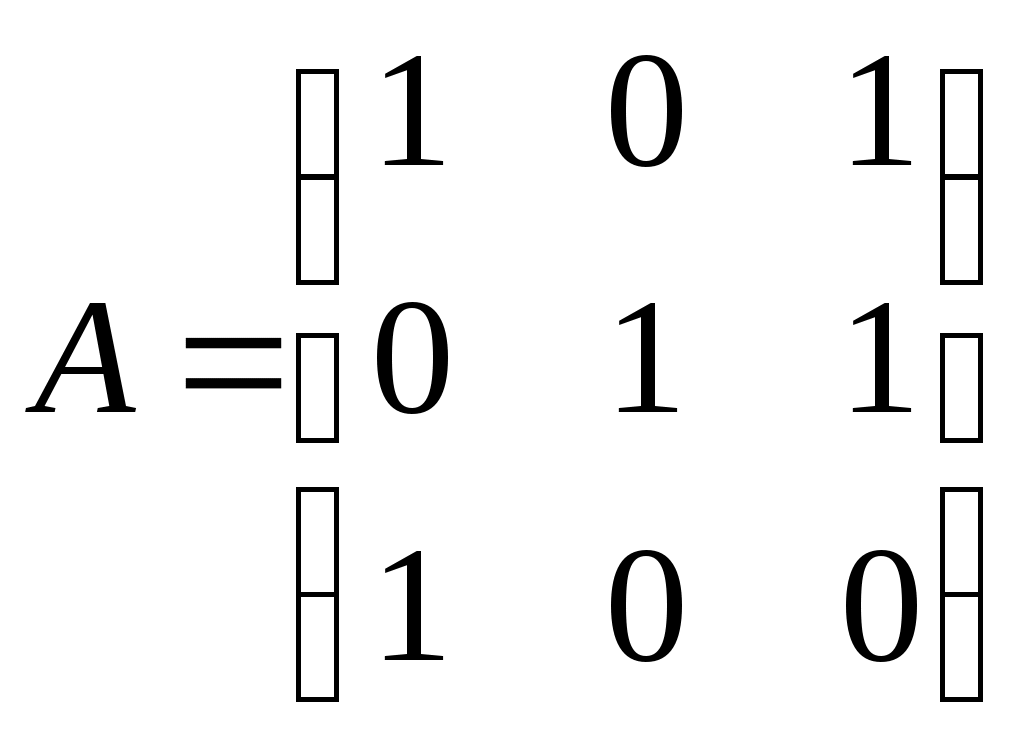 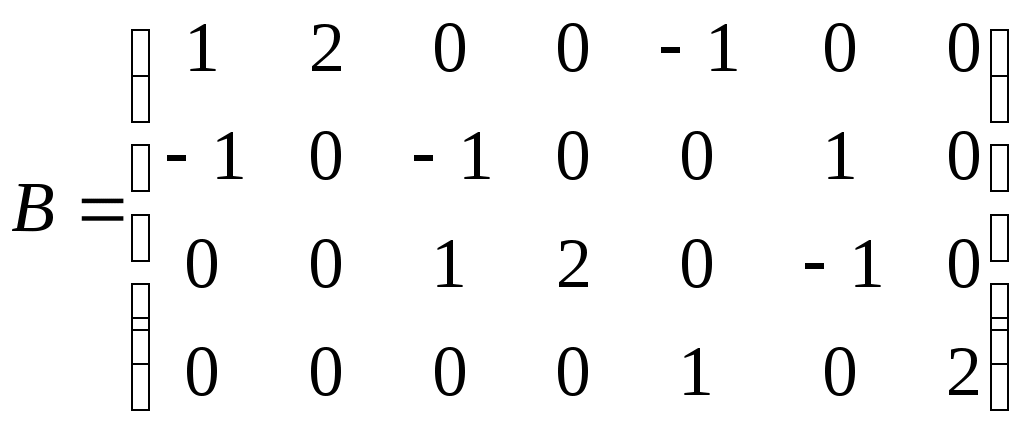 Проверить, является ли число 985 кодом Харари? Восстановить дерево по префиксному коду {001, 010, 0111, 1011, 1101, 1111} Восстановить дерево по коду Прюфера {2, 2,3,3,1,2,4} Написать код Прюфера для данного дерева                 3 34 2   11 12 8 11 12 86      5 7 10 9 5 7 10 9 1 20. Обойти тремя способами бинарное ордерево     а аf   b b    d k s d k sc e u t Нарисовать дерево, соответствующее списку ((а,в,с),(е,(f,i)),g) Написать список висячих вершин данного ордерева             A k s b c d e f Написать СДНФ, СКНФ булевой функции Ответ проверить таблицей истинности. Написать многочлен Жегалкина булевой функции. 25. Проверить на полноту систему булевых функций 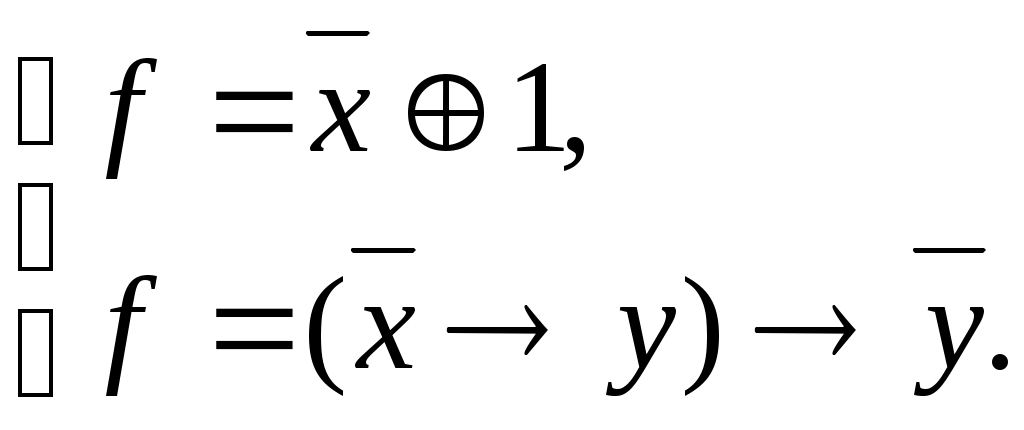 ПЕРЕЧЕНЬ ЗНАНИЙ, НАВЫКОВ И УМЕНИЙ ДЛЯ ПОЛУЧЕНИЯ УДОВЛЕТВОРИТЕЛЬНОЙ ОЦЕНКИ Для получения удовлетворительной оценки студент должен: знать основные понятия, теоремы и формулы, а также уметь применять их при решении типовых задач; усвоить методы решения стандартных задач по следующим разделам дискретной математики: операции над множествами, отношения на множестве, основы комбинаторики, графы, матрица смежности и матрица инцидентности графа, код Харари, деревья, префиксный код ордерева, булевы функции. 9. СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ Андросенко, В.А. Дискретная математика. Методические указания к выполнению практических заданий и задачи для студентов I курса очной формы обучения по направлениям подготовки 230400 «Информационные системы и технологии», 090900 «Информационная безопасность», 040100 «Социология», 090303 «Информационная безопасность автоматизированных систем» II семестр./В.А. Андросенко, К.А. Сенько – Брянск, М.: БГТУ, 2014. – 60с. 2. Асеев, Г. Г. Дискретная математика: учеб. пособие/ Г. Г. Асеев, О. М. Абрамов, Д. Э. Ситников. – Ростов н/Д; Харьков: Феникс: Торсинг, 2003. 3. Гаврилов, Г.П. Задачи и упражнения по дискретной математике/ Г.П. Гаврилов, А.А. Сапоженко. – М.: Физматлит, 2005. 4. Гисин, В.Б. Дискретная математика: учебник и практикум для академического бакалавриата/ В.Б. Гисин. – М.: Издательство Юрайт, 2016. – 383с. 5. Гореленков, А.И. Теория вероятностей и математическая статистика: сб. задач/ А.И. Гореленков, В.М. Кобзев, А.П. Мысютин. – Брянск, БГТУ, 2007. 6. Просветов, Г. И. Дискретная математика: задачи и решения: учебно – практич. пособие/Г. И. Просветов. – М.: Альфа – Пресс, 2013. 7. Пугач, Л. И. Высшая математика. Задачи по дискретной математике, математической логике и теории алгоритмов: метод. указания к практическим занятиям для студентов 1 курса очной формы обучения по специальностям 220400 «Программное обеспечение», 22300 «Системы автоматизированного проектирования» и 075300 «Организация и технология защиты информации»/Л. И. Пугач; БГТУ. – Брянск: Изд – во БГТУ, 2005. Дискретная математика: методические указания к выполнению самостоятельной работы для студентов очной формы обучения по направлениям подготовки 10.03.01 – «Информационная безопасность», 09.03.02 – «Информационные системы и технологии», квалификация «бакалавр», по специальности 10.05.03 – «Информационная безопасность автоматизированных систем», квалификация «специалист». ВАЛЕНТИНА АЛЕКСАНДРОВНА АНДРОСЕНКО Научный редактор В.М. Кобзев Компьютерный набор В.А. Андросенко Темплан 2017г. Подписано в печать 06.04.2017 Формат 6084 1/16. Бумага офсетная Печать офсетная. Усл.печ. л. 1,39 Уч.-изд. л. 1,39. Тираж 1 экз. Брянский государственный технический университет 241035, г. Брянск, бульвар 50 лет Октября, 7, БГТУ Кафедра «Высшая математика», тел. 561477 | |||||||||||
