эконометрика. вариант4. Для анализа зависимости цены автомобиля y от его возраста Х
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Задача 2 Временной ряд В базе данных магазина также содержится информация об объеме ежемесячных продаж автомобилей за прошлый год, представленная в следующей таблице: (таблица 8)
Представить графически ежемесячные объемы продаж автомагазина. На основе визуального анализа построенного графика выдвинуть гипотезу о виде статистической зависимости объема продаж от времени и записать ее математически. Построим график ежемесячных продаж автомагазина: 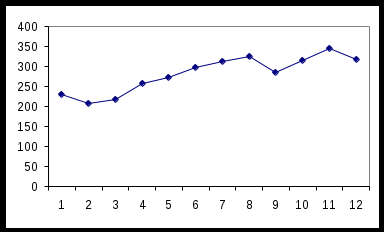 рис. 3 Траектория временного ряда На основе визуального наблюдения ломанной линии динамики продаж можно выдвинуть гипотезу о наличии линейного тренда – устойчивого роста среднего уровня временного ряда. Математически линейная зависимость выразится формулой Методом наименьших квадратов найти оценку уравнения линейного тренда Cоставим вспомогательную таблицу: (таблица 9)
т.к. n=12, то тогда 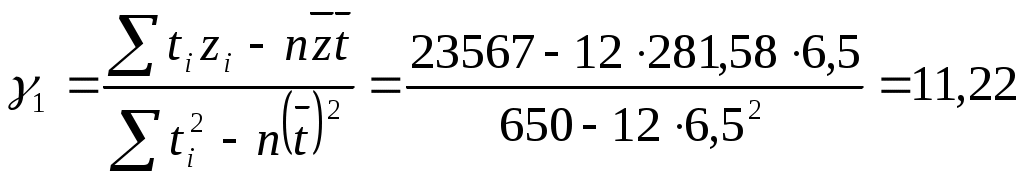 таким образом, получаем уравнение регрессии: 3. Для линии тренда построить доверительную полосу надежности 0,95. Нарисовать ее на графике вместе с линией тренда и исходным временным рядом. Для расчета доверительных интервалов составим следующую таблицу: (таблица 10)
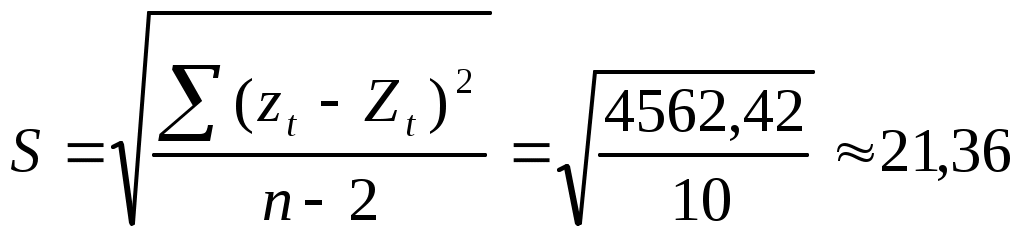 , для каждого ti рассчитаем , для каждого ti рассчитаем 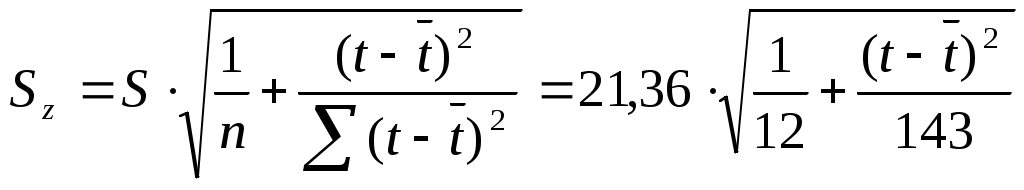 , , Изобразим доверительную полосу (линии Zн и Zв) , линию тренда (Zt), и исходный временной ряд (z t) на графике: (рис. 4) 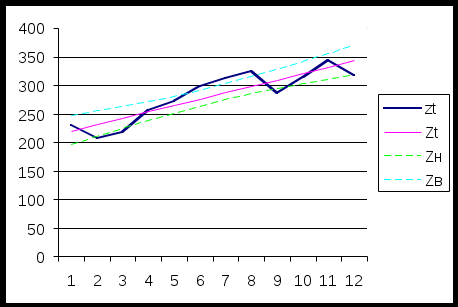 рис. 4 С помощью уравнения тренда найти точечный и интервальный прогноз (надежности 0,95) для среднего объема продаж на конец первого квартала текущего года. В данном случае t = 12+3 = 15. Точечный прогноз: Интервальный прогноз: 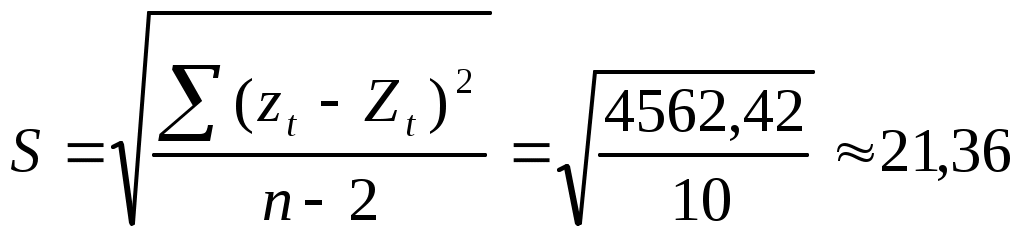 , , 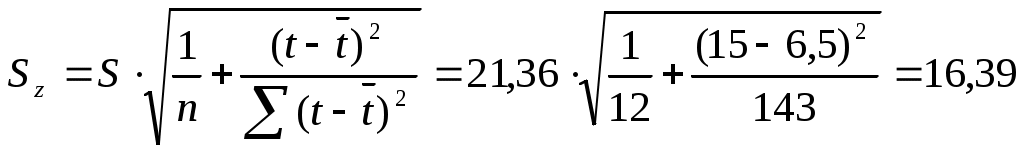 , , Т.е. с надежностью 95% средний объем продаж на конец первого квартала текущего года попадет в интервал (340,4 ; 413,5). Задача 4 Проверка моделей на автокорреляцию и мультиколлинеарность. Для регрессионных моделей Для Вычислим d-статистику Дарбина-Уотсона: 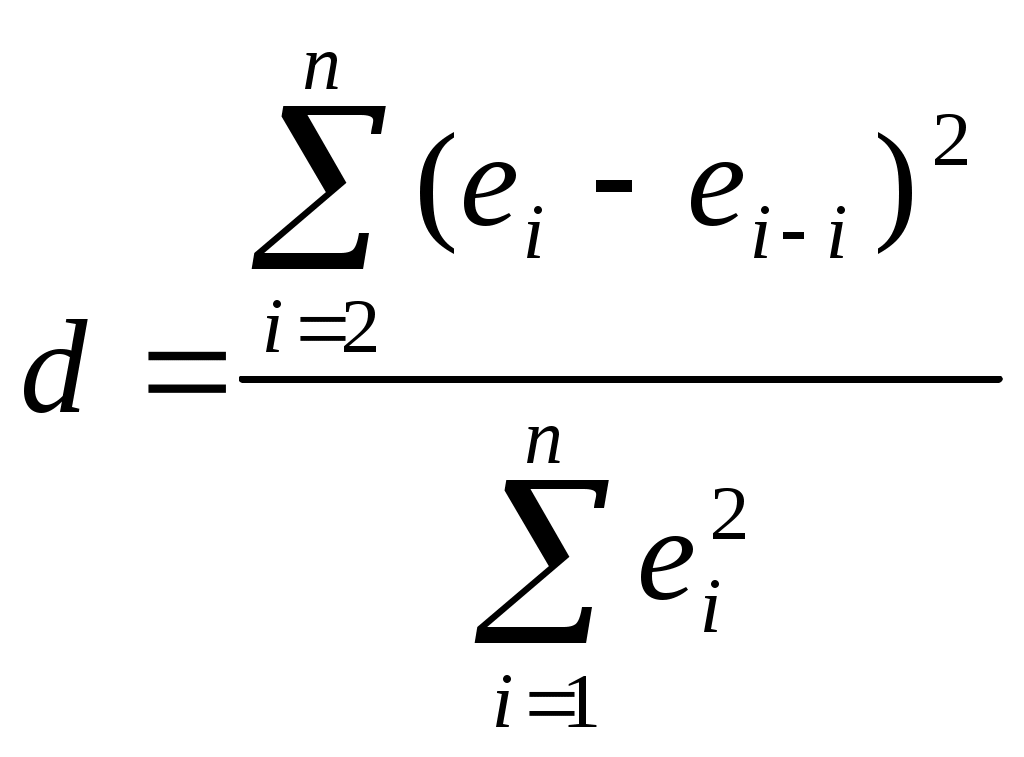 , где , где
Знаменатель нами уже найден, он равен 0,83, тогда |
