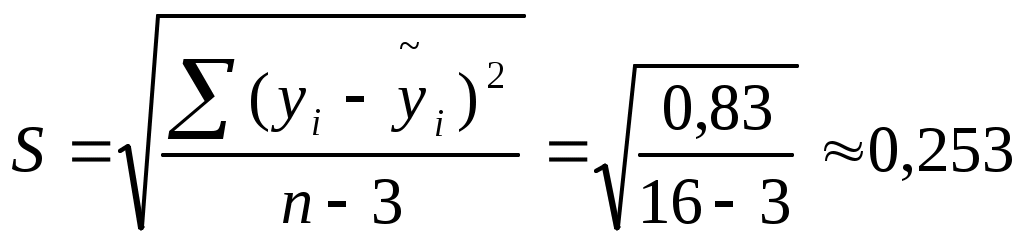2. Множественная зависимость.
2.1. По методу наименьших квадратов найти оценки коэффициентов множественной линейной регрессионной модели 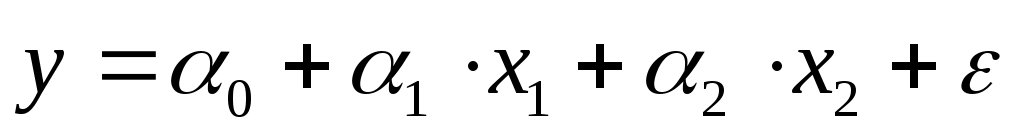
Составим матрицы 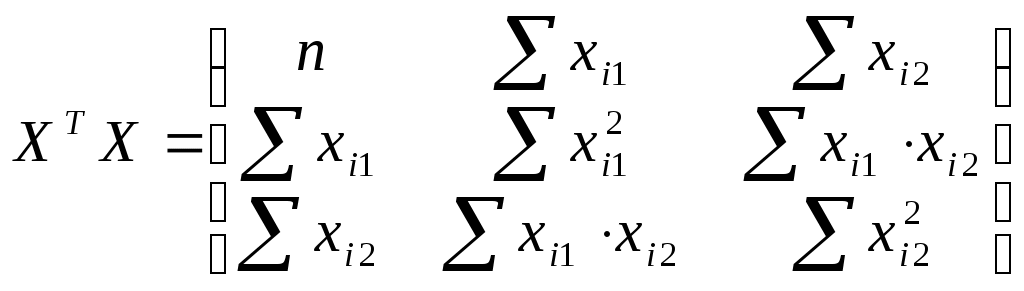 и и 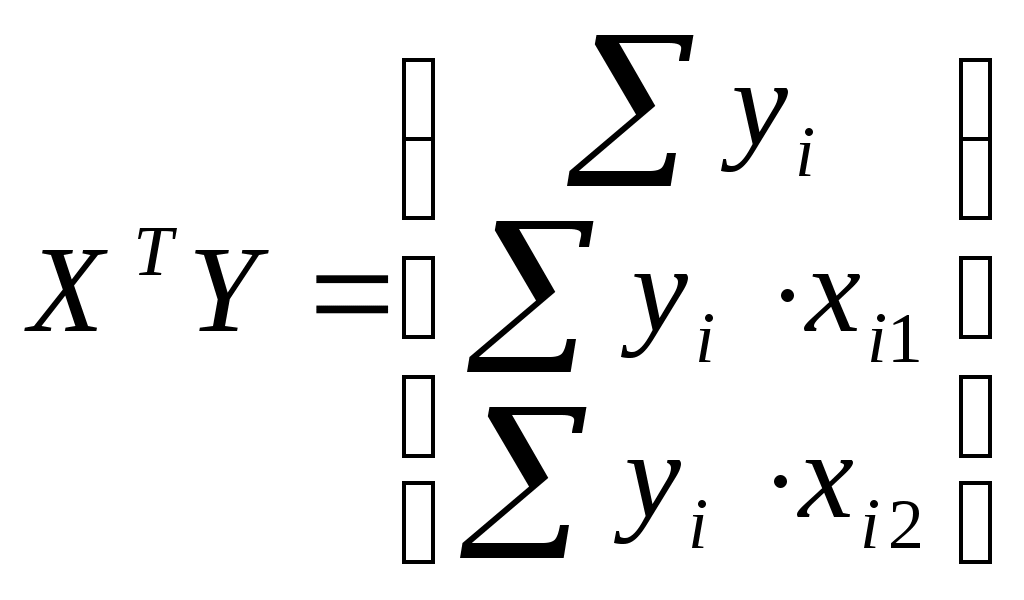
Для этого составим вспомогательную таблицу: (таблица 6)
i
|
yi
|
xi1
|
xi2
|
xi12
|
xi22
|
yi xi1
|
yi xi2
|
xi1xi2
|
1
|
14,4
|
4
|
154
|
16
|
23716
|
57,6
|
2217,6
|
616
|
2
|
16,9
|
2
|
155
|
4
|
24025
|
33,8
|
2619,5
|
310
|
3
|
13
|
5
|
149
|
25
|
22201
|
65
|
1937
|
745
|
4
|
9,6
|
7
|
128
|
49
|
16384
|
67,2
|
1228,8
|
896
|
5
|
9,8
|
7
|
134
|
49
|
17956
|
68,6
|
1313,2
|
938
|
6
|
9,6
|
7
|
127
|
49
|
16129
|
67,2
|
1219,2
|
889
|
7
|
16,8
|
2
|
157
|
4
|
24649
|
33,6
|
2637,6
|
314
|
8
|
14,8
|
4
|
160
|
16
|
25600
|
59,2
|
2368
|
640
|
9
|
9,8
|
7
|
134
|
49
|
17956
|
68,6
|
1313,2
|
938
|
10
|
16,9
|
2
|
154
|
4
|
23716
|
33,8
|
2602,6
|
308
|
11
|
16
|
3
|
161
|
9
|
25921
|
48
|
2576
|
483
|
12
|
17,4
|
2
|
167
|
4
|
27889
|
34,8
|
2905,8
|
334
|
13
|
17,2
|
2
|
163
|
4
|
26569
|
34,4
|
2803,6
|
326
|
14
|
17,4
|
2
|
163
|
4
|
26569
|
34,8
|
2836,2
|
326
|
15
|
15,7
|
3
|
155
|
9
|
24025
|
47,1
|
2433,5
|
465
|
16
|
17,1
|
2
|
162
|
4
|
26244
|
34,2
|
2770,2
|
324
|
Σ
|
232,4
|
61
|
2423
|
299
|
369549
|
787,9
|
35782
|
8852
|
  ; ; 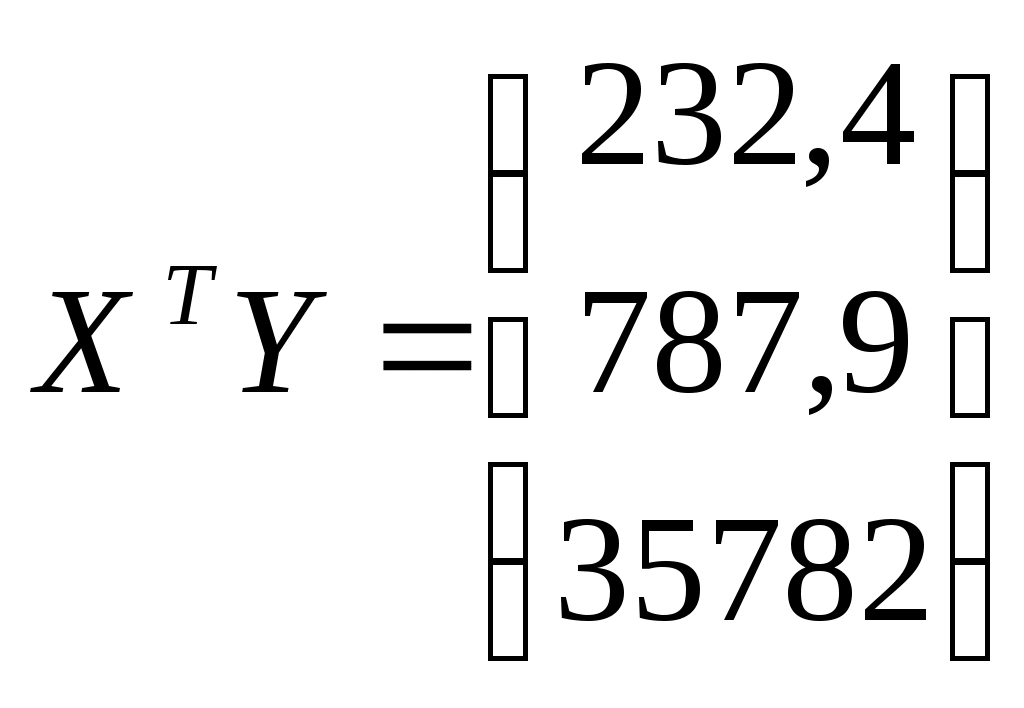
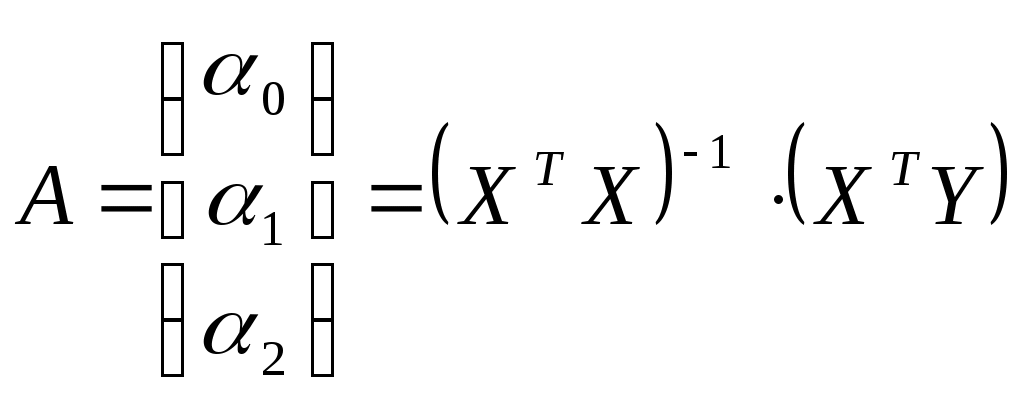
Найдем 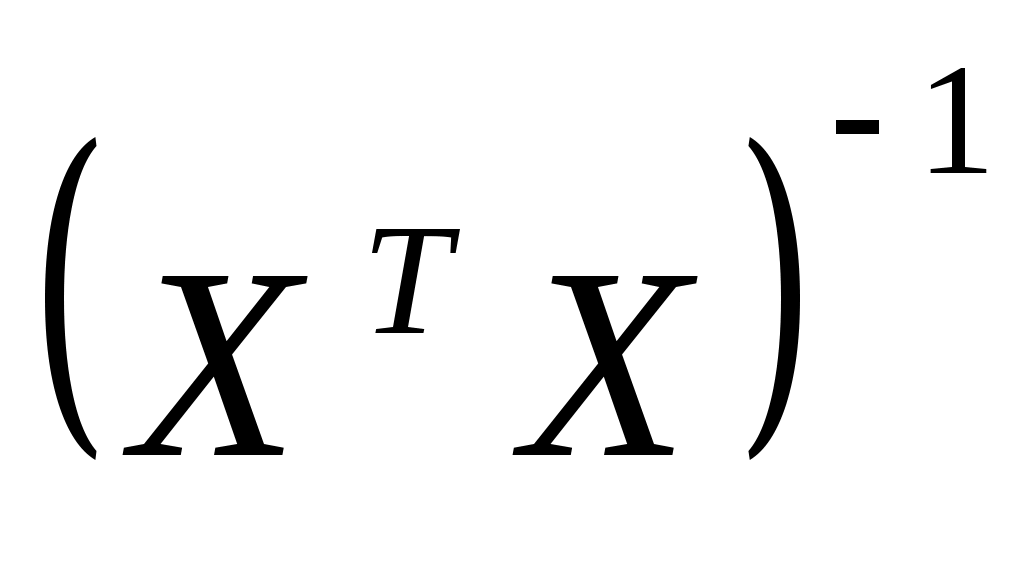 : :
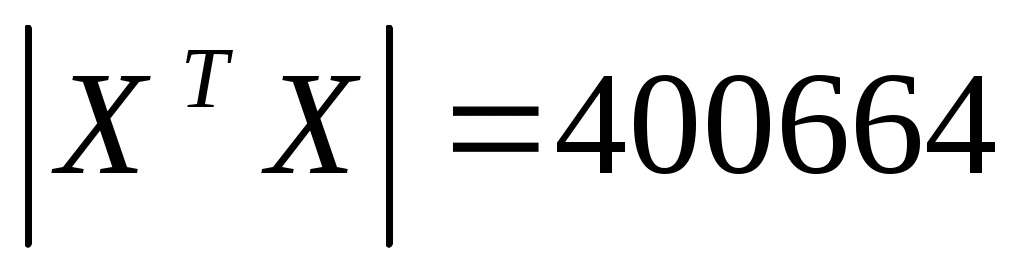
алгебраические дополнения:
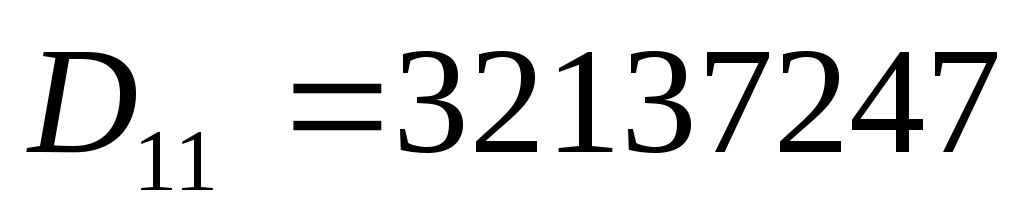 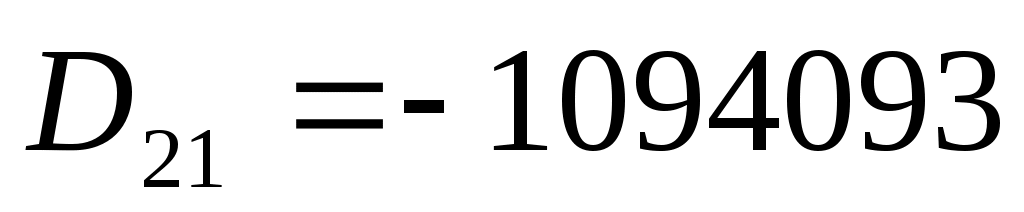 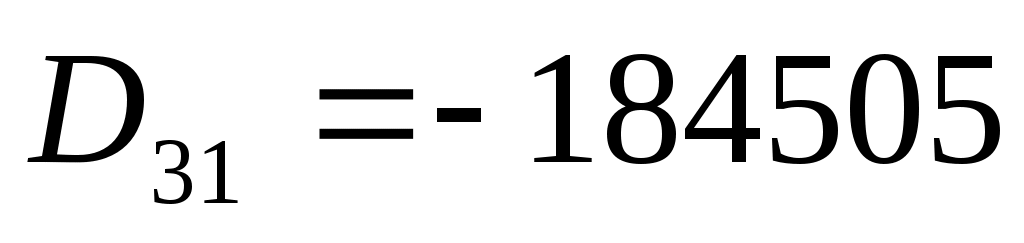
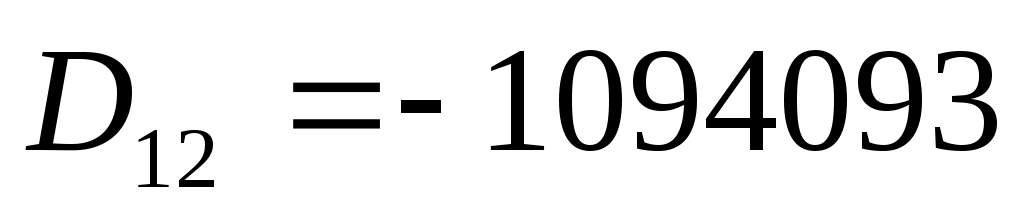 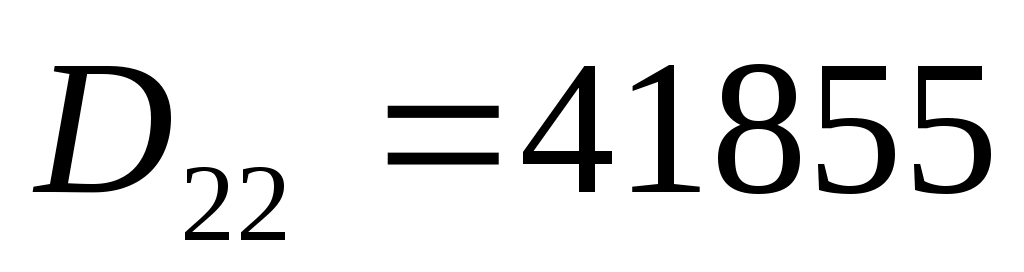 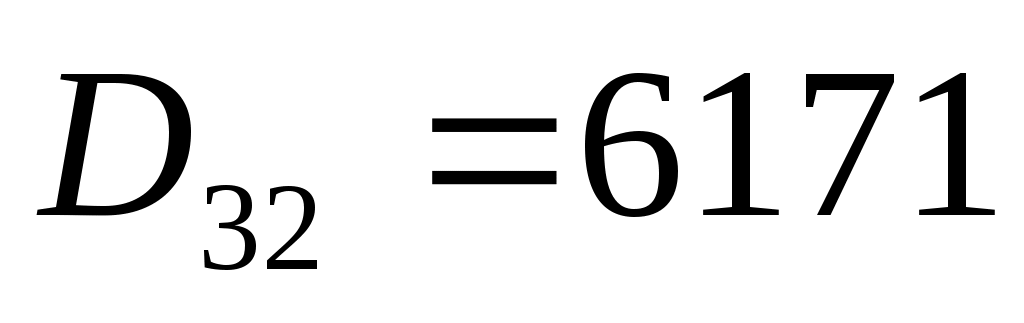
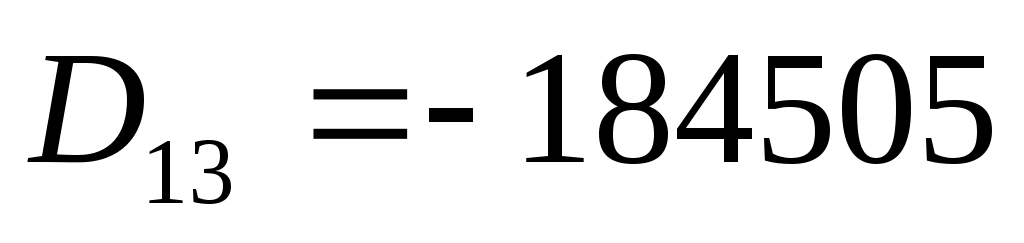 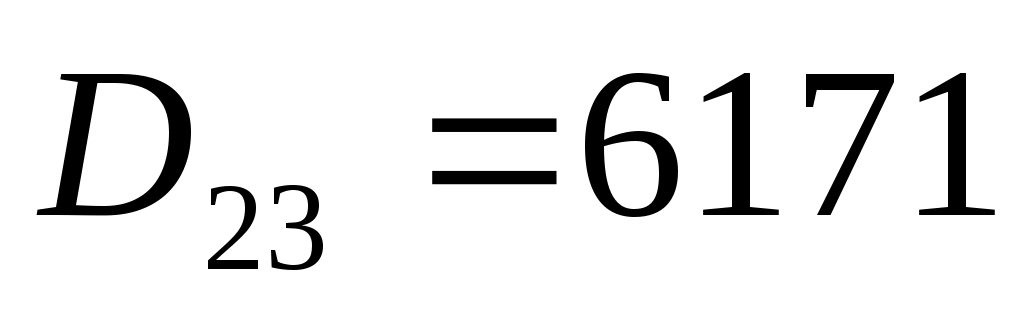 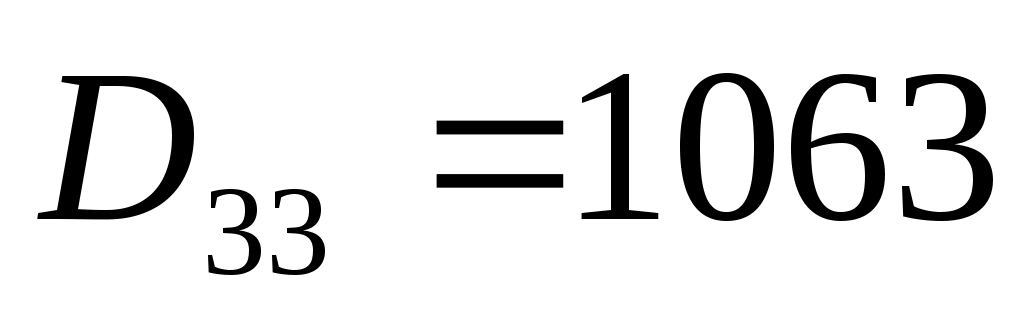
Тогда обратная матрица 
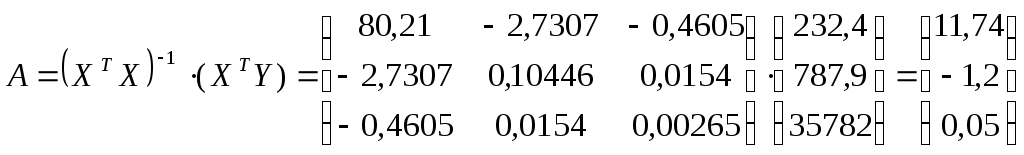 таким образом, получаем уравнение регрессии: таким образом, получаем уравнение регрессии:
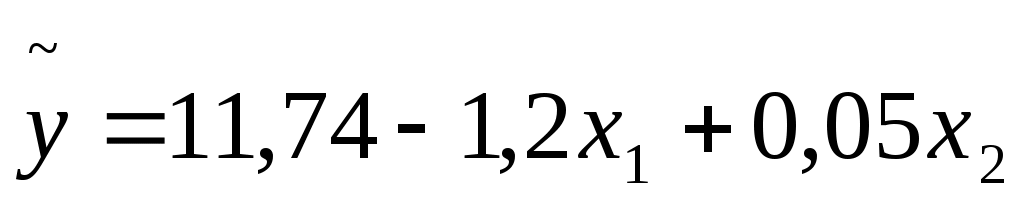 . .
2.2. Проверить статистическую значимость параметров и уравнения множественной регрессии с надежностью 0,9.
Для вычисления коэффициента детерминации составим таблицу: (таблица 7)
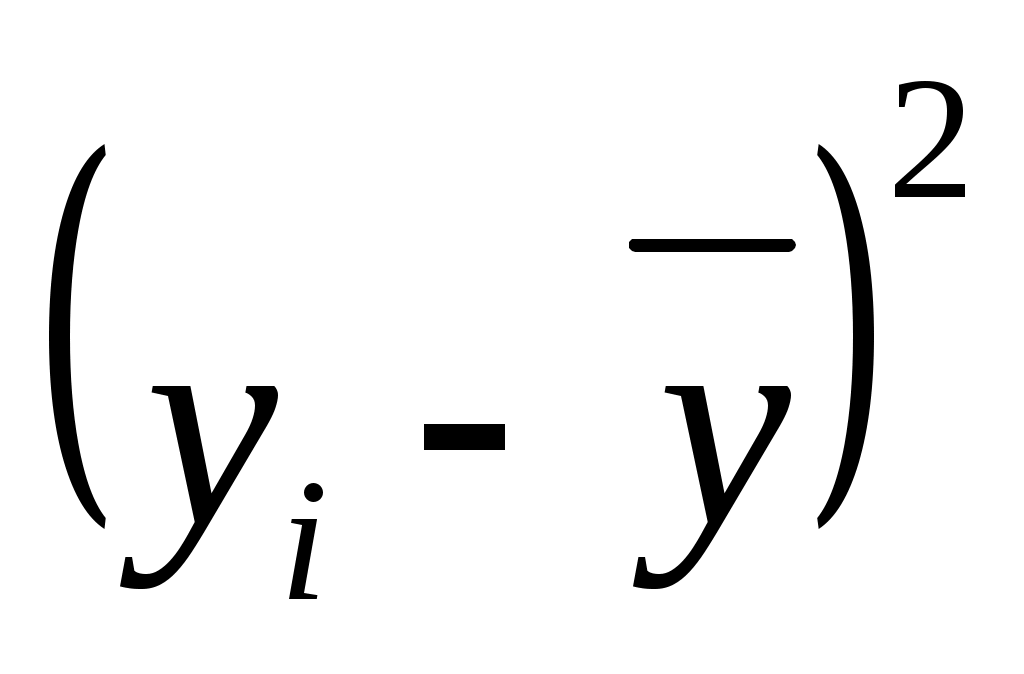
ỹi
|
ỹi -yi
|
(ỹi -yi )2
|
|
14,64
|
0,24
|
0,0576
|
0,015625
|
17,09
|
0,19
|
0,0361
|
5,640625
|
13,19
|
0,19
|
0,0361
|
2,325625
|
9,74
|
0,14
|
0,0196
|
24,25563
|
10,04
|
0,24
|
0,0576
|
22,32563
|
9,69
|
0,09
|
0,0081
|
24,25563
|
17,19
|
0,39
|
0,1521
|
5,175625
|
14,94
|
0,14
|
0,0196
|
0,075625
|
10,04
|
0,24
|
0,0576
|
22,32563
|
17,04
|
0,14
|
0,0196
|
5,640625
|
16,19
|
0,19
|
0,0361
|
2,175625
|
17,69
|
0,29
|
0,0841
|
8,265625
|
17,49
|
0,29
|
0,0841
|
7,155625
|
17,49
|
0,09
|
0,0081
|
8,265625
|
15,89
|
0,19
|
0,0361
|
1,380625
|
17,44
|
0,34
|
0,1156
|
6,630625
|
Σ
|
|
0,83
|
145,91
|
Коэффициент корреляции 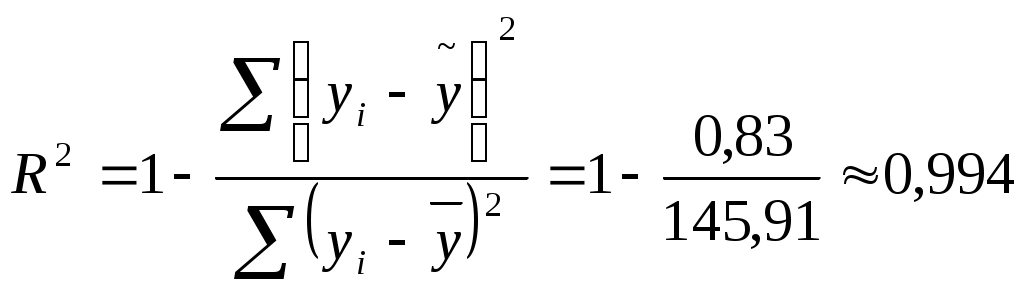
Следовательно, регрессия y на x1 и x 2 объясняет 99,4% колебаний значений у. Это свидетельствует о значительном суммарном влиянии независимых переменных x1 и x 2 на зависимую переменную у.
Качество уравнения множественной регрессии оценим с помощью F-теста, найдем
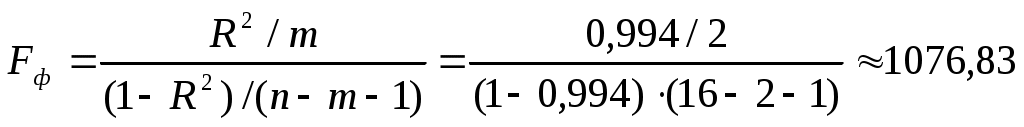
При уровне значимости 0,05 и 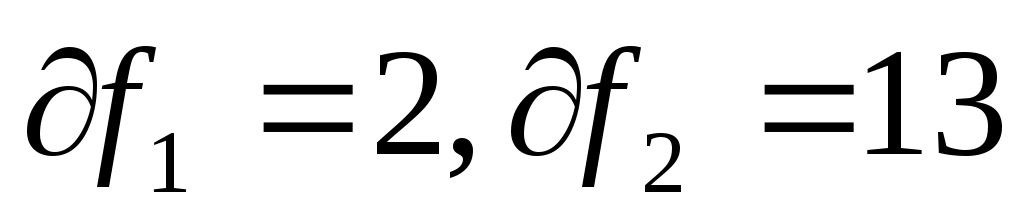 табличное значение Fm=3,81. Неравенство Fmф выполняется, гипотеза о незначимости коэффициентов регрессии отклоняется и признается статистическая значимость уравнения регрессии. табличное значение Fm=3,81. Неравенство Fmф выполняется, гипотеза о незначимости коэффициентов регрессии отклоняется и признается статистическая значимость уравнения регрессии.
2.3. Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей возраста 3 года и мощностью 165 л.с. с доверительной вероятностью 0,9.
Точечный прогноз:
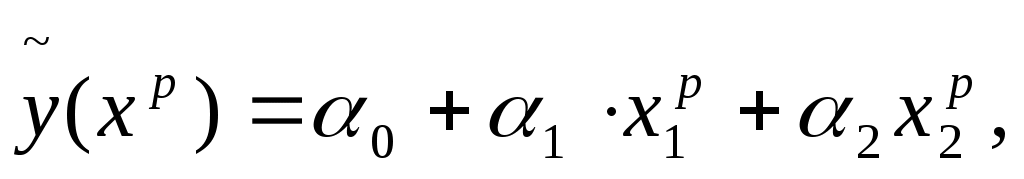 где где 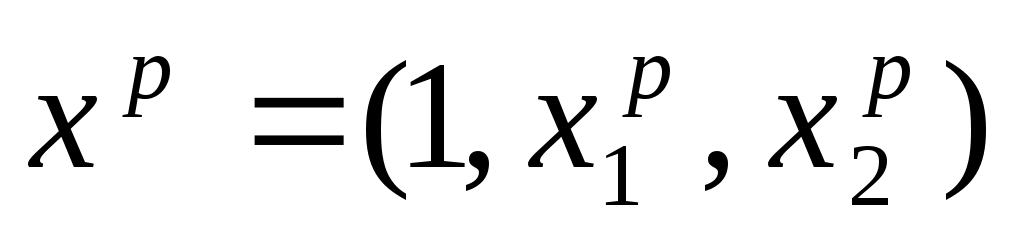 - вектор независимых переменных, для которого определяется прогноз. В нашем случае - вектор независимых переменных, для которого определяется прогноз. В нашем случае 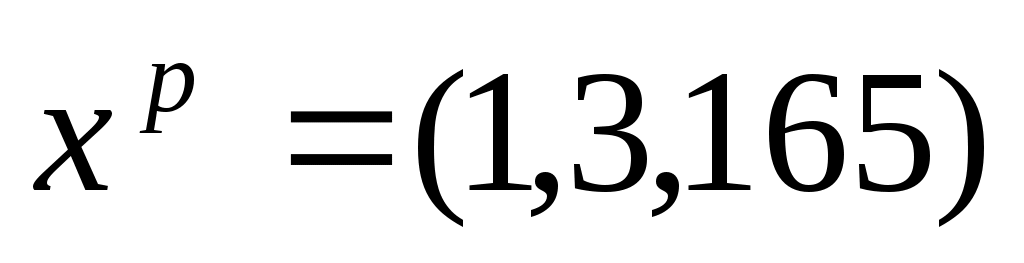
Тогда 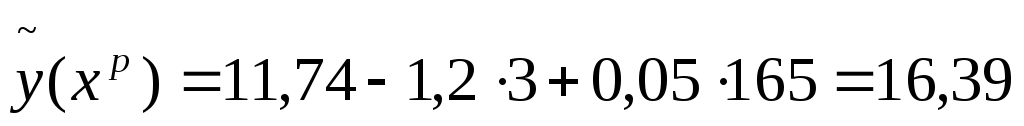
Интервальный прогноз:
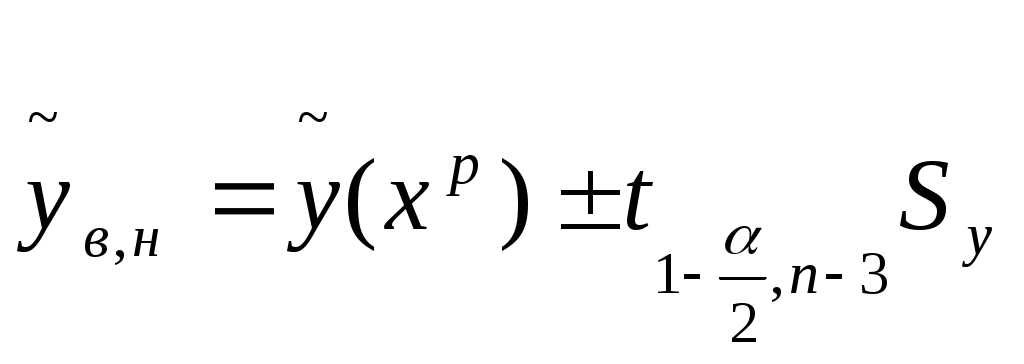 ; ; 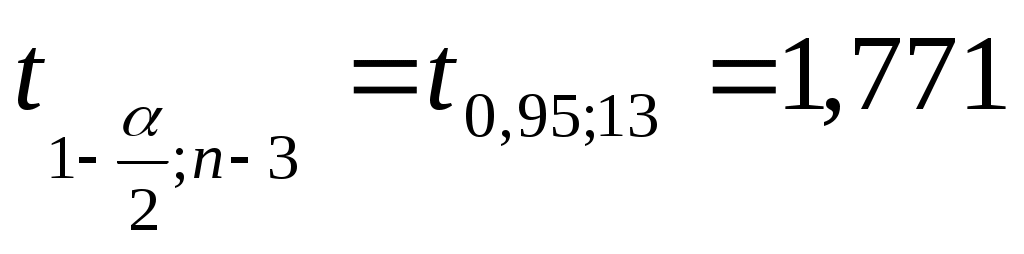
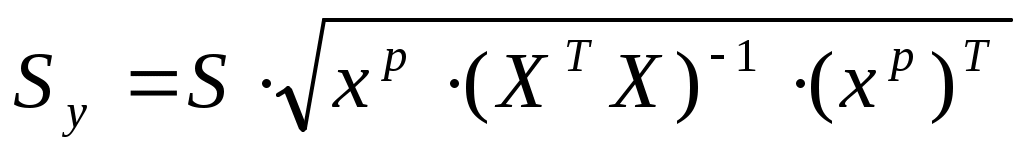 , где , где 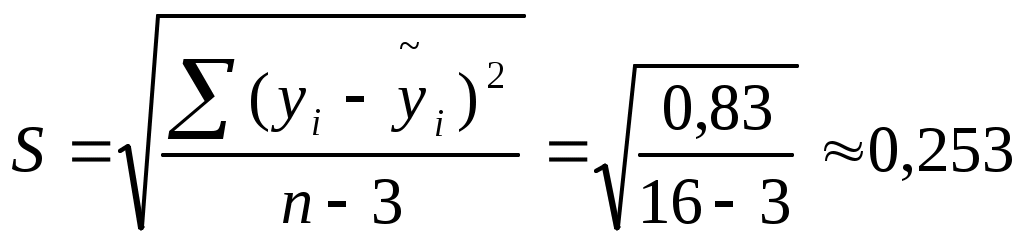
тогда 
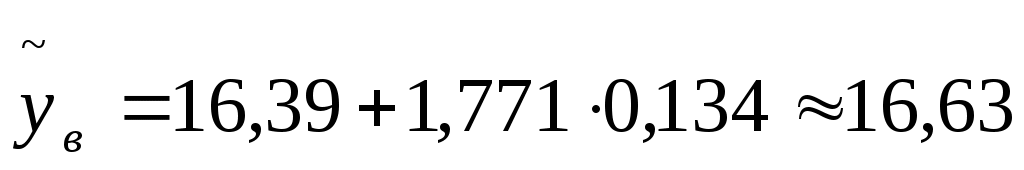
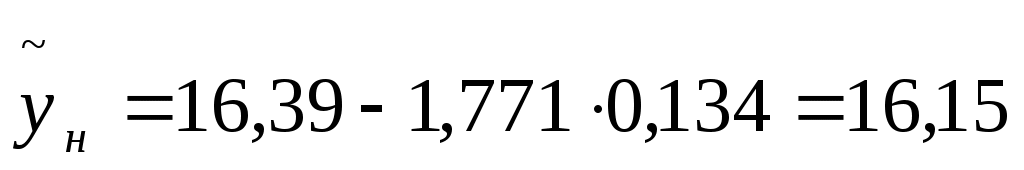
т.е. с надежностью 90% цена на поступившие автомобили попадет в интервал (16,15 ; 16,63).
3. Экономическая интерпретация.
Рассмотрим зависимость цены от возраста:
Так как 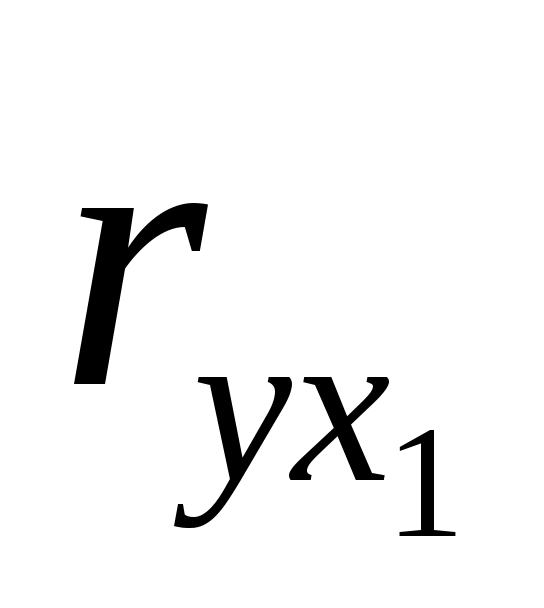 = -0,9966 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная отрицательная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии = -0,9966 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная отрицательная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии  . .
Коэффициент 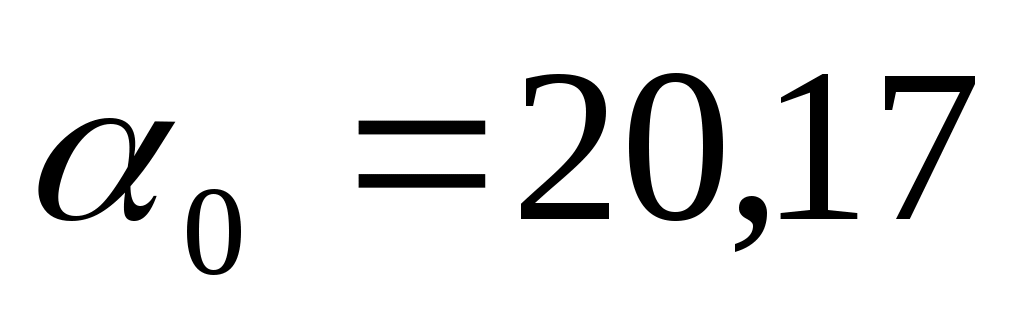 формально определяет цену нового автомобиля, т.е. когда формально определяет цену нового автомобиля, т.е. когда 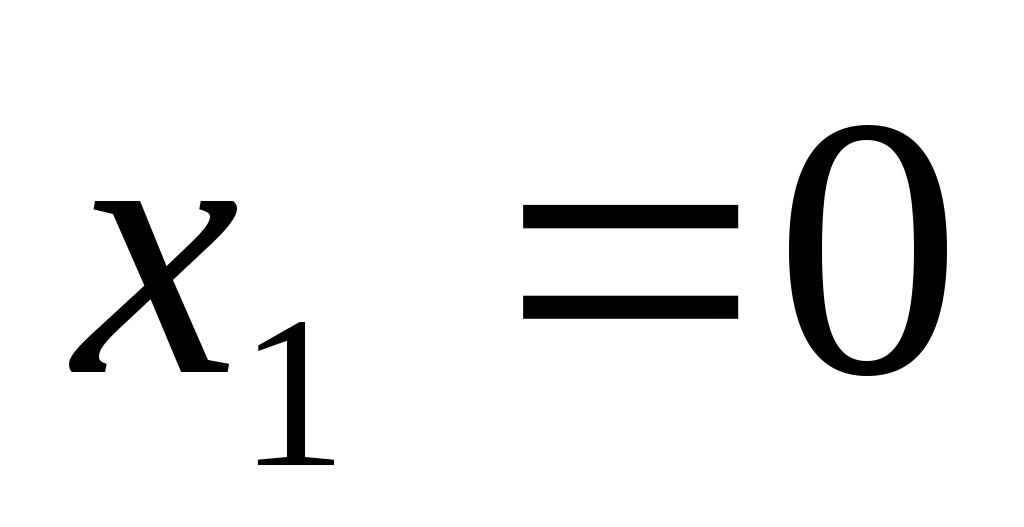 . .
Коэффициент 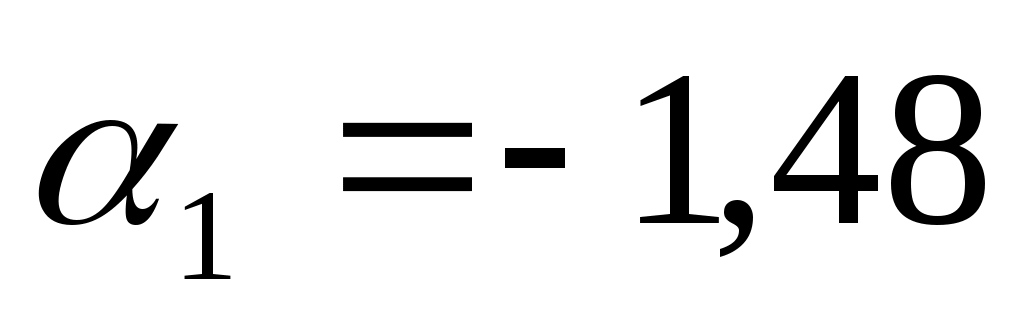 характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении возраста автомобиля на 1 год следует ожидать уменьшения цены на 1,48 тыс. у.е. характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении возраста автомобиля на 1 год следует ожидать уменьшения цены на 1,48 тыс. у.е.
Зависимость цены от мощности:
Так как 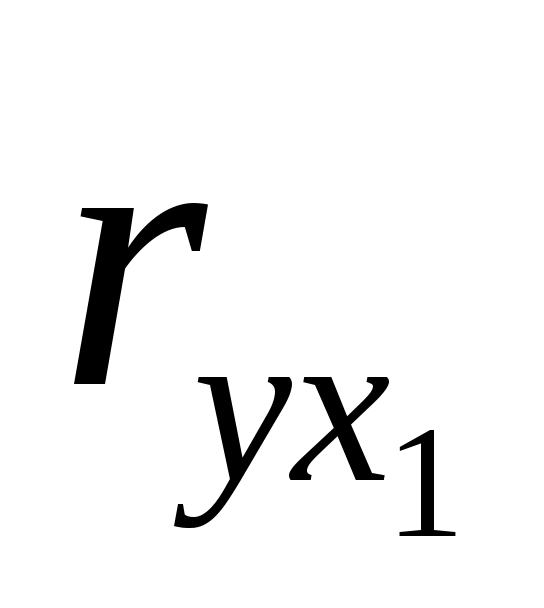 = 0,9516 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии = 0,9516 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии  . .
Коэффициент 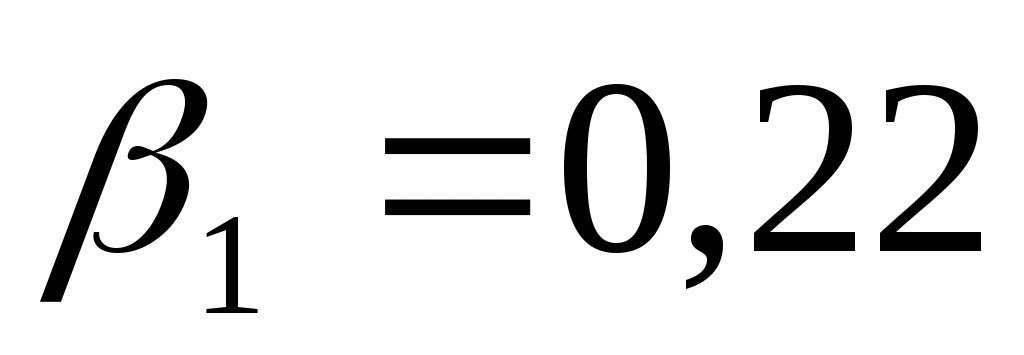 характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении мощности автомобиля на 1 л.с следует ожидать увеличения цены на 0,22 тыс. у.е. характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении мощности автомобиля на 1 л.с следует ожидать увеличения цены на 0,22 тыс. у.е.
В результате исследования зависимости объема цены от двух факторов – возраста и мощности двигателя получено уравнение множественной регрессии 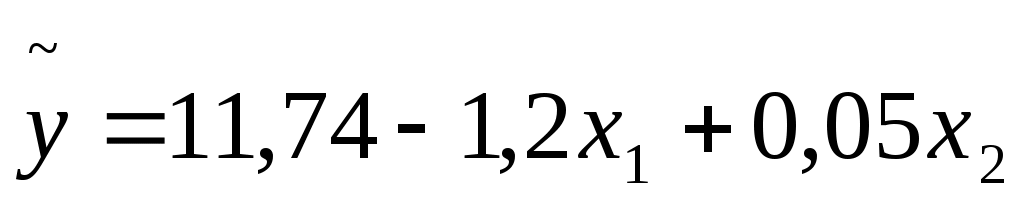
Коэффициент 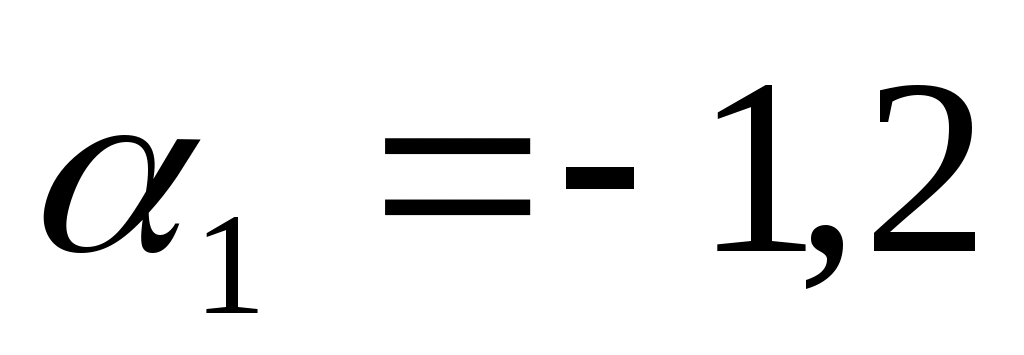 показывает, что при увеличении возраста на 1 год и неизменной мощности двигателя следует ожидать снижения цены автомобиля на 1,2 тыс. у.е. показывает, что при увеличении возраста на 1 год и неизменной мощности двигателя следует ожидать снижения цены автомобиля на 1,2 тыс. у.е.
Коэффициент 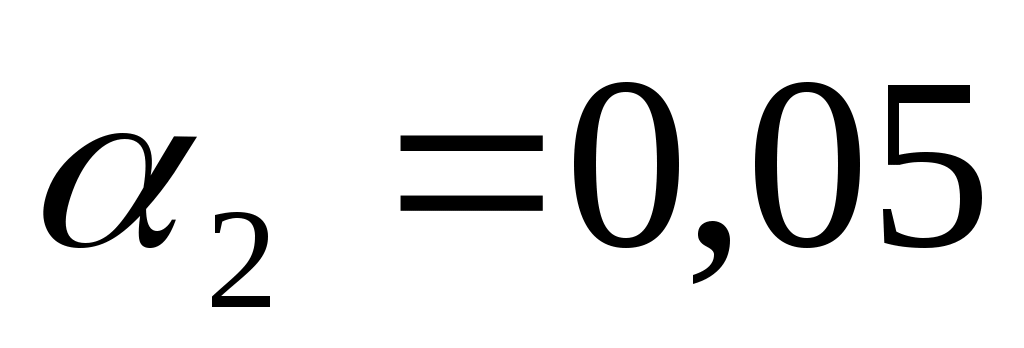 показывает, что при увеличении мощности на 1 л.с и неизменном возрасте следует ожидать увеличения цены автомобиля на 0,05 тыс. у.е. показывает, что при увеличении мощности на 1 л.с и неизменном возрасте следует ожидать увеличения цены автомобиля на 0,05 тыс. у.е.
|
 Скачать 0.63 Mb.
Скачать 0.63 Mb.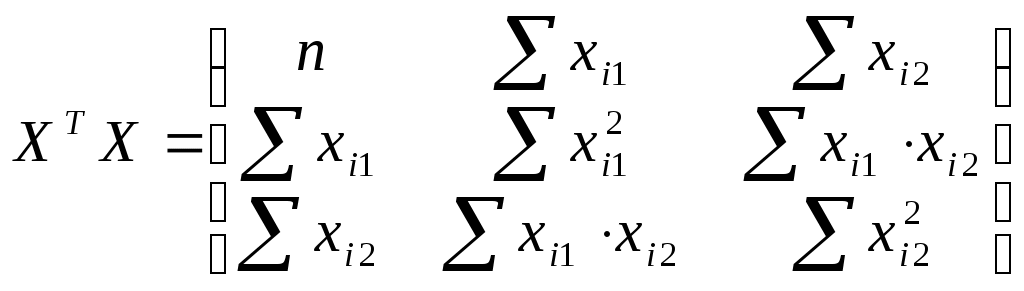 и
и 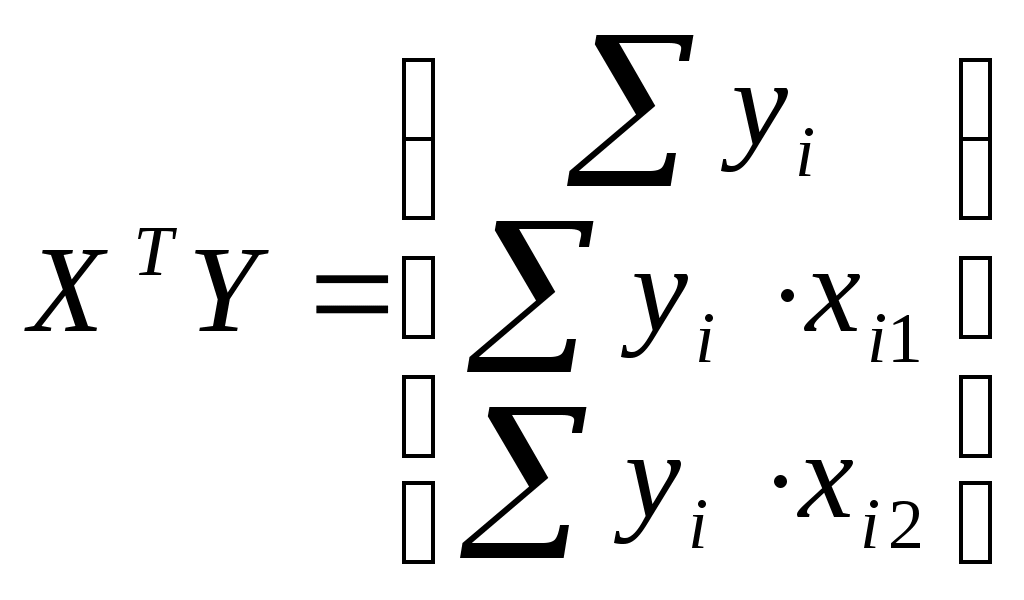
 ;
; 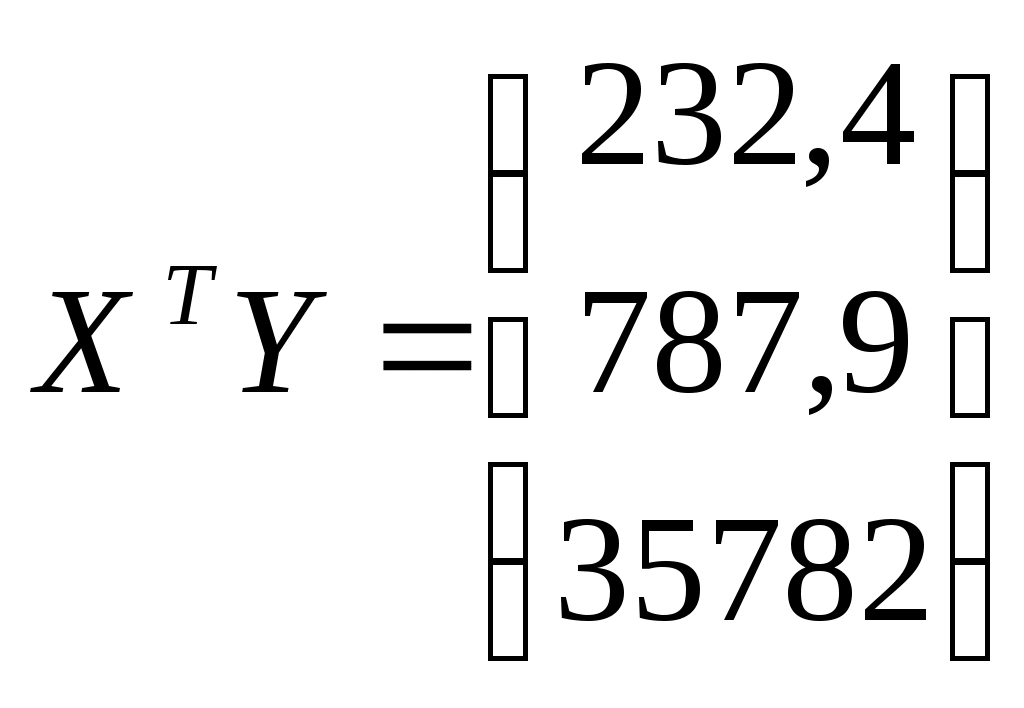
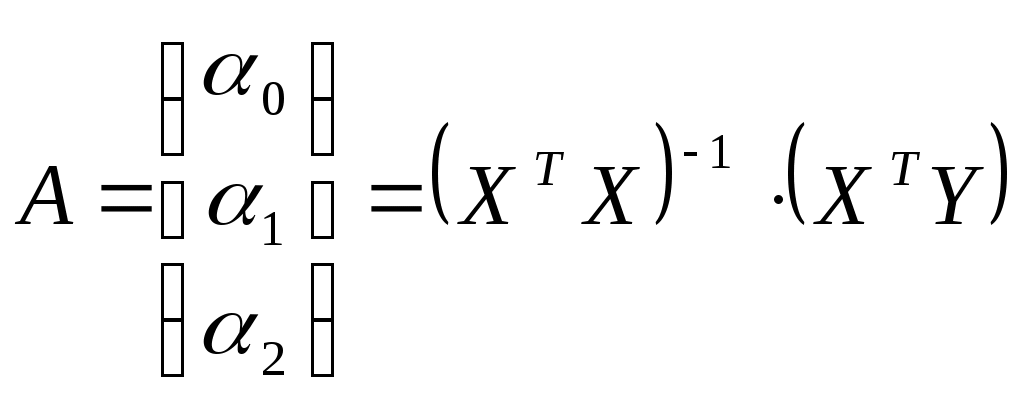
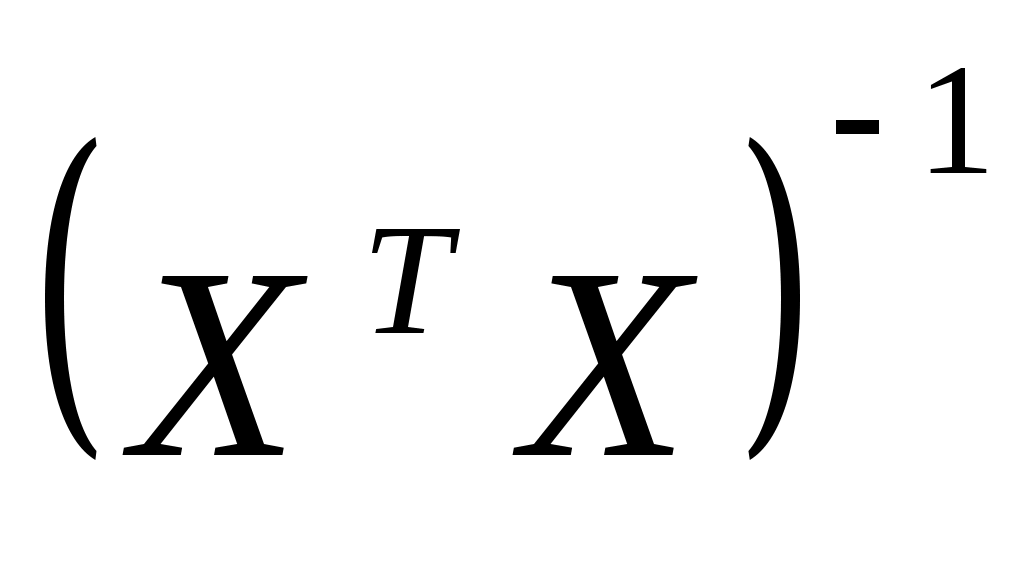 :
:
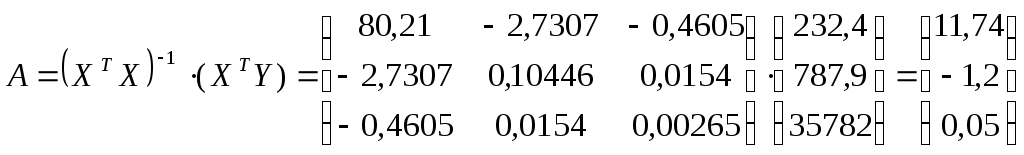 таким образом, получаем уравнение регрессии:
таким образом, получаем уравнение регрессии: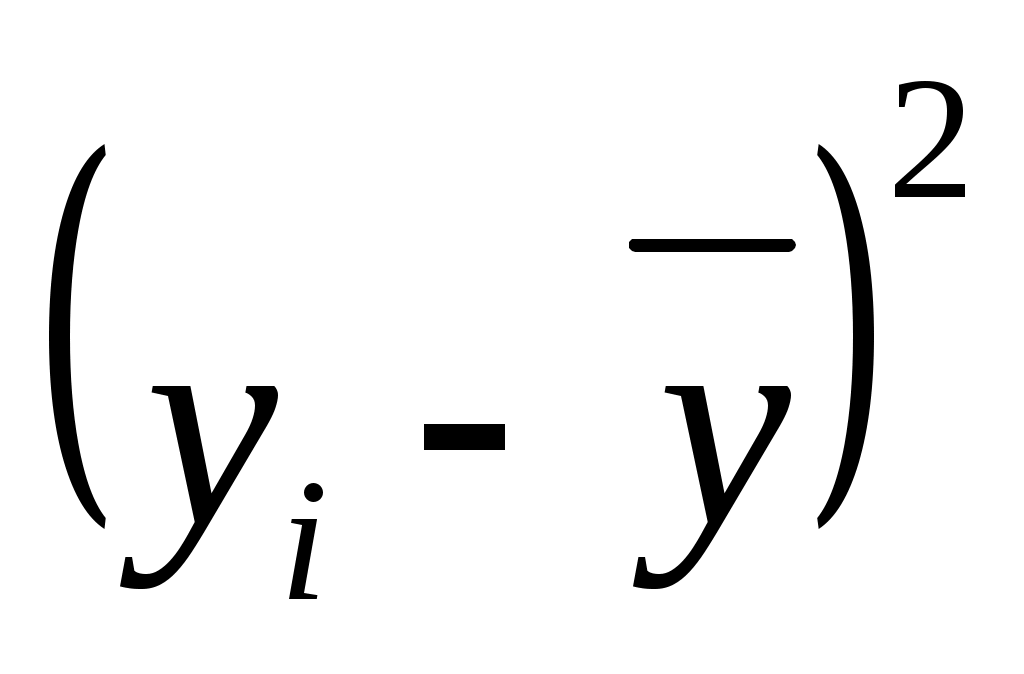
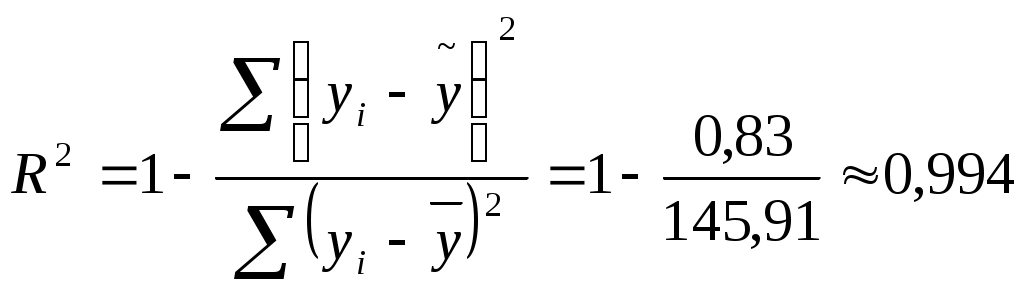
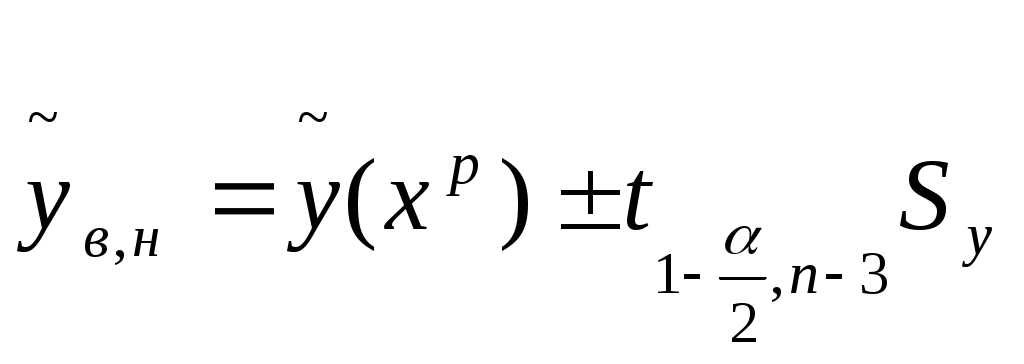 ;
;