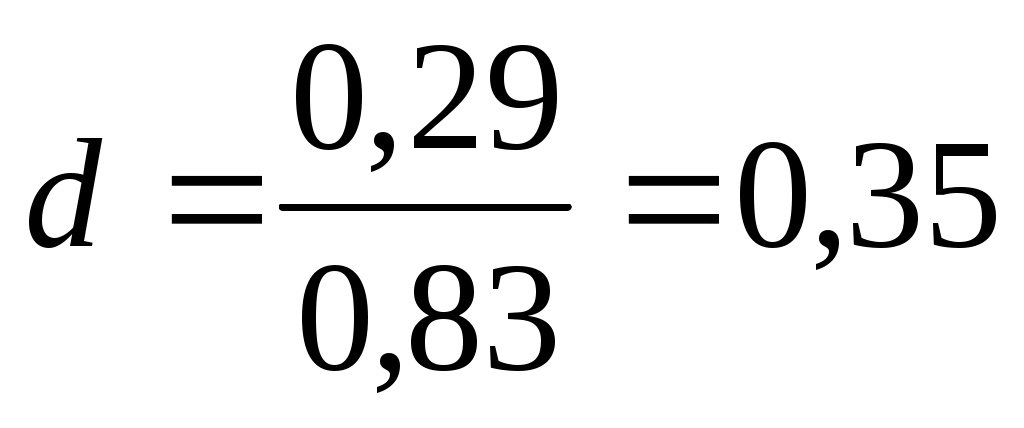 Табличные критические значения для уровня значимости α = 0,01, число наблюдений 16, число независимых переменных 2, равны: Табличные критические значения для уровня значимости α = 0,01, число наблюдений 16, число независимых переменных 2, равны:
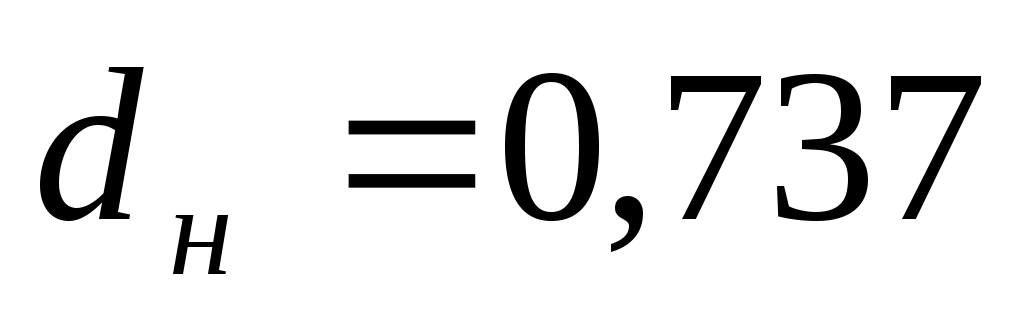 и и 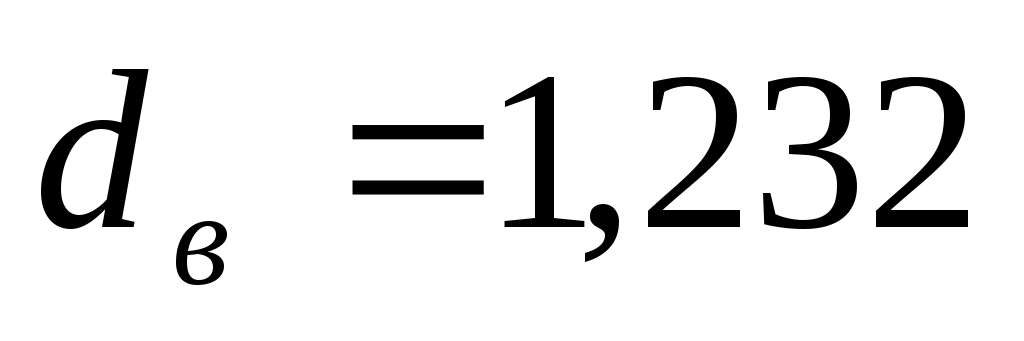 так как так как 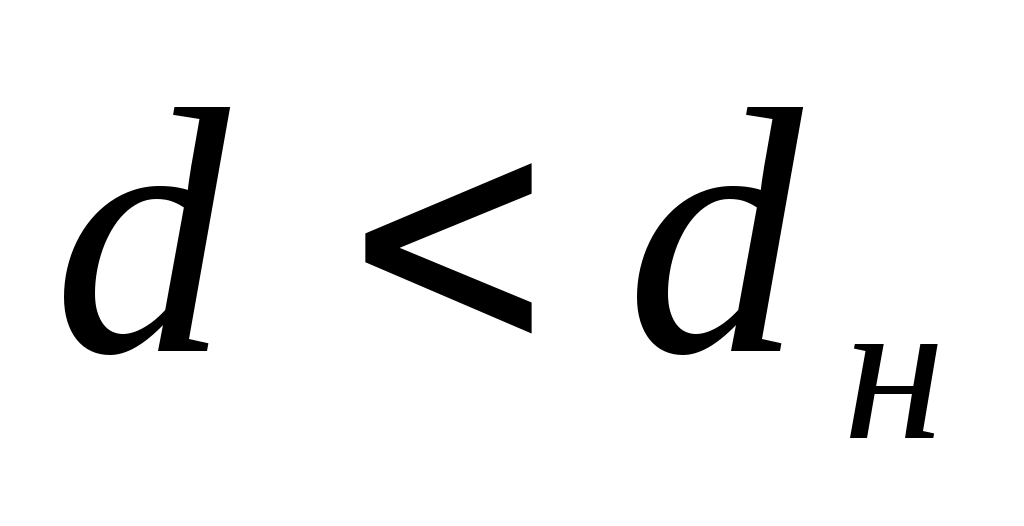 , то делаем вывод о наличии автокорреляции. , то делаем вывод о наличии автокорреляции.
Для 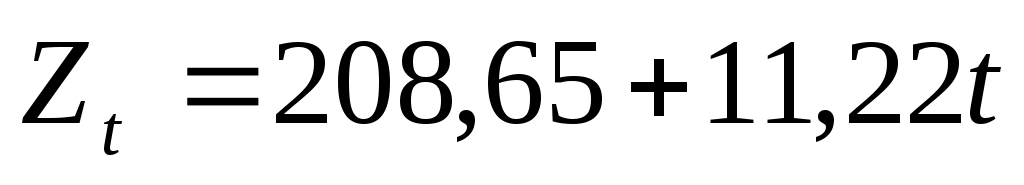 : :
|
(ei –ei-1)2
|
|
1103,568
|
|
1,4884
|
|
828,2884
|
|
14,2884
|
|
218,4484
|
|
14,2884
|
|
0,0484
|
|
2422,608
|
|
281,5684
|
|
352,6884
|
|
1385,328
|
Σ
|
6622,61
|
тогда 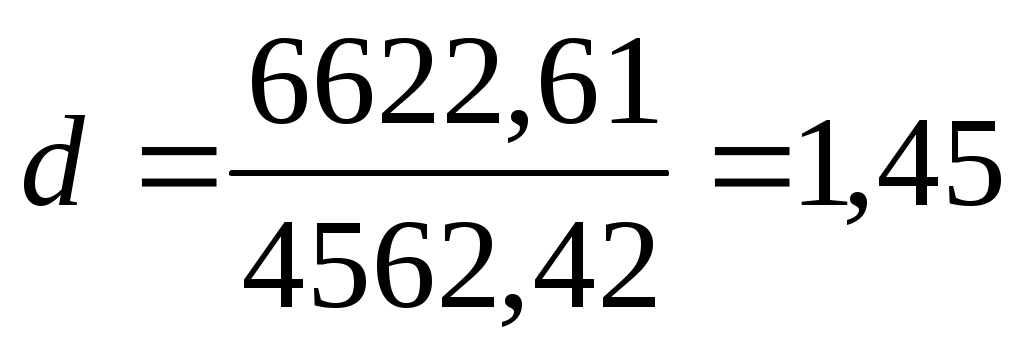 Табличные критические значения для уровня значимости α = 0,01, число наблюдений 12, число независимых переменных 1, равны: Табличные критические значения для уровня значимости α = 0,01, число наблюдений 12, число независимых переменных 1, равны:  и и 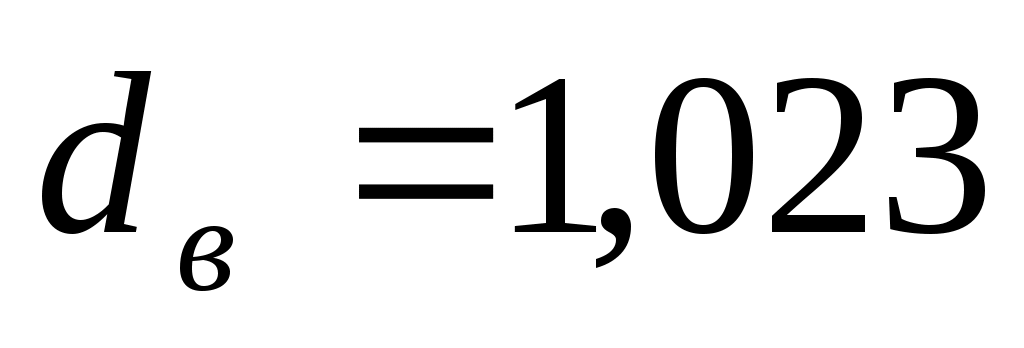 .Так как .Так как 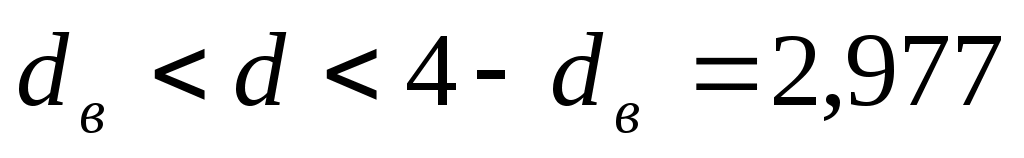 , то делаем вывод об отсутствии автокорреляции. , то делаем вывод об отсутствии автокорреляции.
Для регрессионной модели 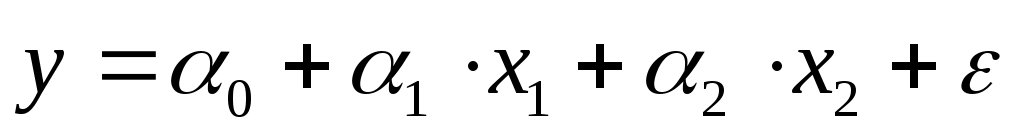 проверить наличие или отсутствие мультиколлинеарности, используя: проверить наличие или отсутствие мультиколлинеарности, используя:
а) парный коэффициент корреляции (приближенно);
б) критерий «хи-квадрат» на уровне значимости α = 0,01.
а). Рассмотрим уравнение регрессии 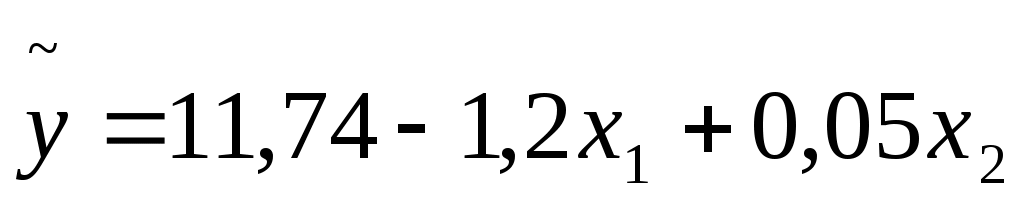
вычислим значение коэффициента корреляции между объясняющими переменными х1 и х2:
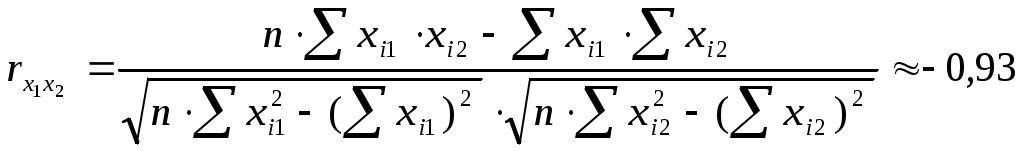 Найдем Найдем
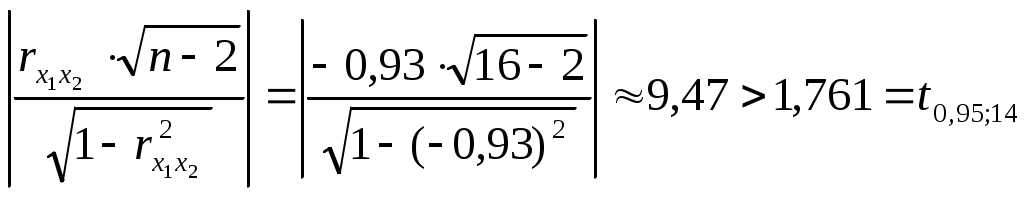 , тогда коэффициент парной корреляции , тогда коэффициент парной корреляции 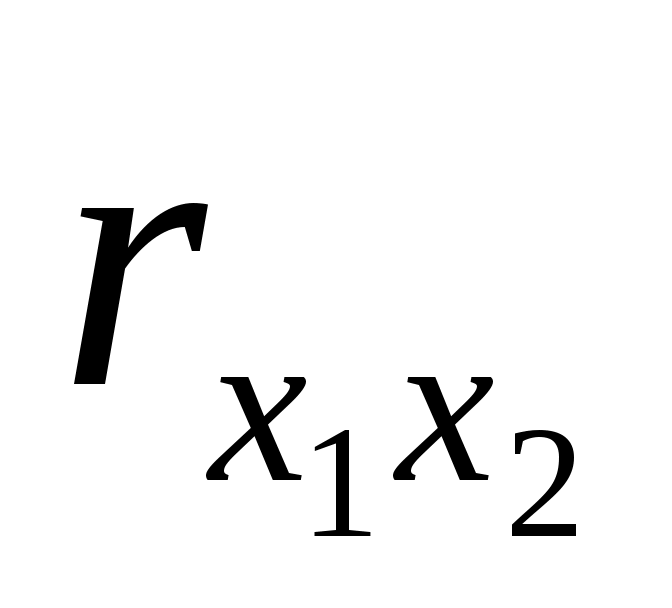 значительно отличается от нуля, т.е. можно считать что переменные значительно отличается от нуля, т.е. можно считать что переменные 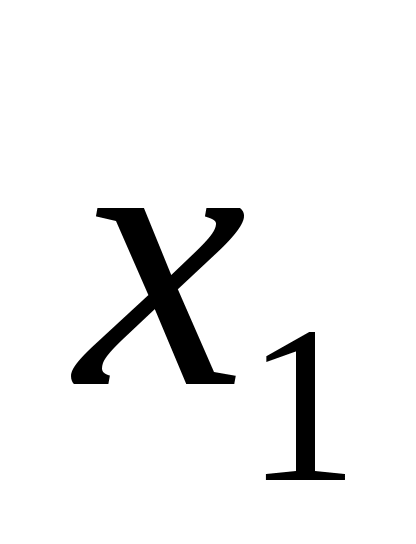 и и 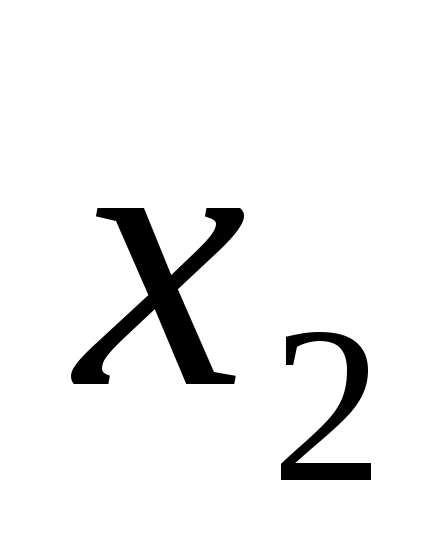 коррелируют между собой и, следовательно, есть мультиколлениарность. коррелируют между собой и, следовательно, есть мультиколлениарность.
б). Рассчитаем определитель матрицы коэффициентов парной корреляции:
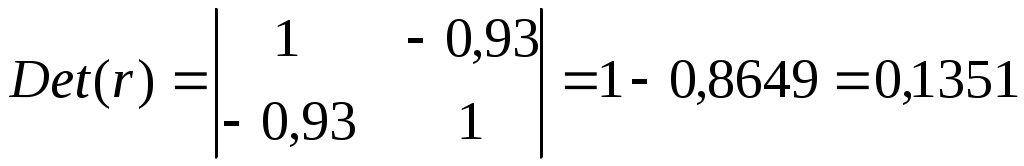
тогда 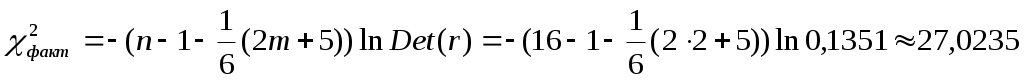
Табличное значение статистики для df = 1 и α = 0,01 равно 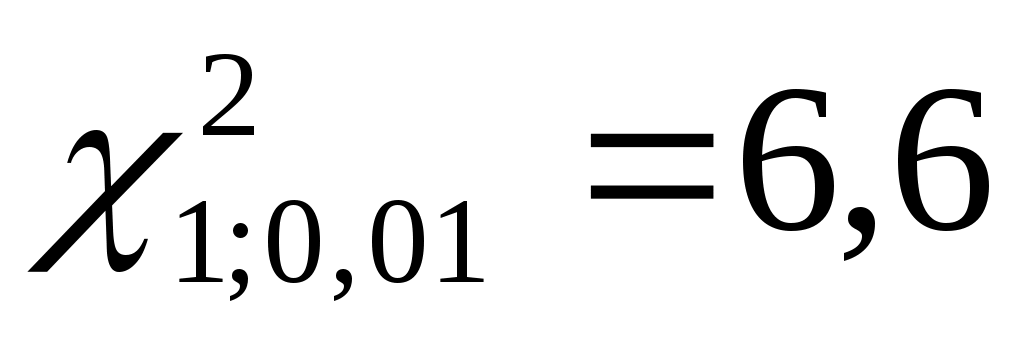 
Так как 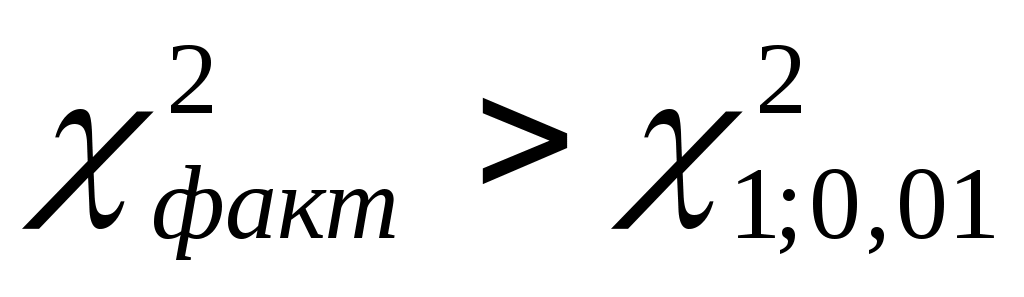 , то подтверждается наличие мультиколлинеарности. , то подтверждается наличие мультиколлинеарности. |
 Скачать 0.63 Mb.
Скачать 0.63 Mb.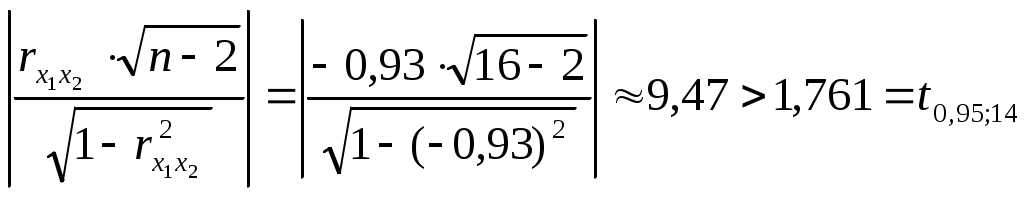 , тогда коэффициент парной корреляции
, тогда коэффициент парной корреляции 