Доклад Математика в природе
 Скачать 469.02 Kb.
|
|
| «Разве ты не заметил, что способный к математике изощрен во всех науках в природе?» (Платон) |
История лесного хозяйства России
Лес есть единство сообщества деревьев, почвы и климата.
Изначально лес для человека был истоком, средой обитания, как океан для рыбы.
В 1832 г. императором Николаем I были утверждены статусы первого в России Общества для поощрения лесного хозяйства, основанного «для поощрения частных владельцев к бережливому сохранению лесов и распространения познаний о правильном лесоводстве». Общество получало казенную субсидию и имело право «давать медаль особого штемпеля». Общество издавало «Лесной журнал».
.Были определены фундаментальные триединые цели лесного хозяйства:
1. охранять леса от истребления;
2. извлекать из них наибольший доход;
3. умножать леса на территориях, в них нуждающихся.
Они остаются неизменными на протяжении более чем 150 лет и только в зависимости от политической и экономической ситуации в стране могли и получали разные приоритеты.
Так выглядел первый лесной журнал.
Математика и природа.
Природа не настолько глупа, чтобы не подчинить всё законам математики
Еще Галилей сказал: «…природа говорит языком математики: буквы этого языка – круги, треугольники и иные математические фигуры». Во времена средних веков, это было более чем ново.
Перечень предметов, исследуемых наукой, с тех пор изменился в сторону увеличения. Математика сложилась на основе наблюдения, операций подсчёта, измерения и описания форм реальных объектов. Если весь существующий мир подчинен одним и тем же законам, то на основе таких наблюдений можно установить хотя бы простейшее из них.
В природе первое, что бросается в глаза, это наличие симметрии. Узнать симметрию исследуемого тела достаточно легко. Для этого требуется взять зеркало, и приложить его посередине исследуемого объекта. Если та часть предмета, что находится на матовой, не отражающей стороне зеркала, тождественна отражению, то объект симметричен (зеркальная симметрия).
Ученый в области хроматографических и масс-спектрометрических методов исследования органических соединений доктор химических наук, профессор И.Г. Зенкевич в своей книге «Эстетика урока математики» утверждает, что «…среди бесконечного разнообразия форм живой и неживой природы в изобилии встречаются такие совершенные образцы, чей вид неизменно привлекает наше внимание: кристаллы, многие животные и растения.
Основу многих форм, созданных природой, составляет симметрия, точнее все её виды – от простейших до самых сложных.
Среди цветов наблюдается поворотная симметрия. Многие цветы обладают характерным свойством: цветок можно повернуть так, что каждый лепесток займёт положение соседнего, цветок совместится с самим собой. Такой цветок обладает поворотной осью симметрии.
В пространстве существуют тела обладающие винтовой симметрией. Винтовая симметрия наблюдается в расположении листьев на стеблях большинства растений. Располагаясь винтом по стеблю, листья как бы раскидываются во все стороны и не заслоняют друг друга от света».
Симметричность обнаруживается в различных структурах, явлениях, также неживой природы, особенно в кристаллах. Кристаллы – это твердые тела, имеющие форму многогранника. Симметрия кристалла является следствием его внутренней симметрии - упорядоченного взаимного расположения в пространстве атомов (молекул), например симметрия сахара, поваренной соли, алмаза, песка, камня, льда, снежинок и так далее. Для каждого вещества существует своя, идеальная форма его кристалла.
По справедливому замечанию немецкого математика, лауреата премии Лобачевского Германа Клауса Гуго Вейля, у истоков симметрии лежит математика.
На геометрические фигуры в существующем мире многие обращали внимание. Так, пчелиные соты являются самым известным природным шестиугольником. Цилиндрическую форму имеют шишки ели.
Спирали очень широко распространены в природе, особенно в биологическом мире (раковины моллюсков, молекулы ДНК, рога баранов, коз, антилоп). По спирали расположены семена в подсолнечнике.
Дальнейшее развитие математики неизбежно охватывает и те направления, на которых лежат более сложные законы все той же единой природы. Рано или поздно разные пути исследований – математических, физических, биологических – вновь пересекаются между собою. Станислав Лем в «Сумме технологий» отмечает: математики стараются охватить все возможные структуры. Именно благодаря такой всеядности на складе математических моделей рано или поздно накапливаются и те, что пригодны для реальности – какова бы эта реальность ни была.
Словом, математика – язык самой природы.
Очень много интересных фактов, математических заданий , задач связаны с нашей природой как для старших школьников так и для самых маленьких. Вот некоторые из них.
Красота природы
Прекрасны наши леса, удивительно хороши деревья. Но милее всех наша береза. Нет, наверное, человека, который не любовался бы нежной белоствольной красавицей. Березовая роща всегда светла, чиста. Русские березы! Как часто мы думаем в дальних путешествиях и мысленно связываемся через них с родной землей, с бескрайними просторами, перелесками, опушками, осенними грибами! Как часто слышим мы от наших знакомых и друзей из разных уголков мира, немного с упреком, немного с раздражением – и что вы нашли в русских березах?! Но с этим мы рождаемся, потому что любовь к березе имеет свою историю и связана с давними традициями русского народа, с его культурой и бытом.
Берестяные грамоты и посуда, березовый сок и березовый веник для бани – все это пришло из далекого славянского прошлого. И лечили березой, и обогревались, и украшали ее на великие языческие праздники, и водили хороводы средь березок и пели о них песни и славили их красоту.
С давних времен береза считается символом России. Почему же именно береза пользовалась на Руси такой популярностью? Береза – это едва ли не самое распространенное дерево в России. Береза всегда
сопутствовала русскому человеку. Летом в тени березы можно было укрыться от солнца, зимой березовые дрова хорошо согревали, на бересте в древности писали, из нее же плели короба и шкатулки, а уж сколько древнеславянских обрядов и обычаев связано с березой, и не пересчитать!
Невозможно представить Россию без берёзы. Берёза – это едва ли не самое распространённое дерево в России, стройное, белое, с раскидистыми ветвями и шелестящими на лёгком ветру листьями. Каждый из нас, любуясь красотой того или иного дерева, интересуется его возрастом. Как же узнать его , не спиливая дерево. Я предлагаю Вам рассмотреть несколько способов определения возраста дерева и выполнить практическую работу.
Д
еревья могут жить очень долго. Порой продолжительность жизни дерева достигает нескольких сотен, а то и тысяч лет. Как определить возраст дерева если дата его высадки неизвестна?Возраст дерева можно определить несколькими способами, все они условно разделены на две группы.
Способы определения возраста дерева:
Не деструктивные – это такие, которые позволяют определить возраст дерева, не нанося ему увечий и не уничтожая его. Сюда мы относим подсчет мутовок, измерение диаметра ствола.
Деструктивные – предполагают, что для определения нужно спилить дерево или нарушить целостность ствола тем самым травмируя растение. Так можно определить возраст дерева по кольцам, а также определить возраст дерева по диаметру ствола.
Д
ля начала определимся, что такое мутовки.Мутовки – это ветви, расположенные веерообразно на стволе дерева.
Такой способ определения возраста дерева подходит в основном для деревьев хвойных пород.
В чем же суть метода? Хвойные деревья образуют новые мутовки каждый год жизни, соответственно посчитая их мы сможем примерно понять сколько лет дереву.
Существует два способа такого подсчета:
Нужно посчитать мутовки, которые находятся выше уровня груди человека и прибавить к ним единицу. (единицу прибавляем, что бы учесть нынешнюю крону дерева);
Нужно посчитать все мутовки, находящиеся на дереве и прибавить к получившемуся числу 3 – если меряете возраст сосны, 4 – если определяете возраст ели, 5 – если нужно узнать возраст пихты и 10 – если речь идет о кедре. Разные цифры прибавляем потому, что первые мутовки на разных хвойных появляться в разном возрасте, например, у сосны не ранее чем в три года и так далее.
Этот способ самый простой, но и результат дает не до конца точный. Зато не требует уничтожения дерева.
Э
то еще один способ определения возраста дерева без нанесения ему вреда. Он более сложный чем предыдущий, так как требует определенных знаний и подготовки, но применять его можно, в отличии от первого, к любой породе дерева.Для того, чтобы определить возраст дерева по диаметру ствола Вам необходимо:
- измерить толщину (обхват) ствола с помощью рулетки. Измерять нужно на уровне не менее одного метра от земли;
- далее необходимо вычислить диаметр ствола (здесь не обойтись без познаний в математике, толщину ствола необходимо разделить на 3,14);
- последний этап - нужно разделить уже вычисленный вами диаметр ствола на средний годовой прирост данной породы дерева. Эту информацию нужно поискать в интернете.
Следует учесть, что прирост дерева зависит от многих факторов, таких как климат, условия, место где растет дерево, потому полученный результат можно оценивать лишь как приблизительный.
Определяем возраст дерева по кольцам.
Это один из наиболее распространённых и достоверных методов определения возраста дерева.
Но подойдет он вам лишь в том случае если определить нужно возраст уже срубленного дерева, так как определяется возраст ствола по спилу. Для этого вам необходимо всего лишь посчитать кольца, которые имеются на спиле ствола дерева. Кольца эти образуются каждый год, потому их и называют годичные кольца соответственно количество колец=возрасту дерева. Определить возраст дерева по кольцам можно даже если самого дерева уже нет, по пню, который от него остался. Начинать подсчет необходимо с цента и двигаться к краям. На спиле вы увидите светлые (образованные весной) и темные кольца (образовавшиеся летом) считать нужно либо только светлые, либо только темные. Следует учесть, что дерево при воздействии на него неблагоприятных факторов окружающей среды, может несколько лет не образовывать годовые кольца, так что результат подсчета тоже будет приблизительным. Ну и если возраст дерева несколько сотен лет, то подсчет займет у вас не мало времени).
Лес – это не только украшение земли. Это ценнейшее сокровище нашей природы. Лес необходим для строительства сел и городов, фабрик и заводов, гидроэлектростанций. Производство бумаги и кинопленки, искусственного волокна и мебели, музыкальных инструментов и спортивного инвентаря не может обойтись без древесины. Древесина служит сырьем для получения массы ценных химических продуктов: спирта, кислот, канифоли. Высококачественный русский лес охотно покупают многие страны.
Что мы сможем сделать, чтобы сохранить наши леса
Бережно относится к учебникам, НЕ менять учебники каждые три года.
НЕ бросать мусор в лесу, и на природе.
Собирать и сдавать макулатуру для вторичной переработки!
По подсчетам экспертов, переработка одной тонны макулатуры не только спасает 10 деревьев, но и экономит 230 кубометров воды, 1500 кВт электроэнергии, ионизированный кислород, достаточный для 30 человек, а также предотвращает выброс 1700 кг СО2. Значит, с начала работы станции на переработке одной только бумаги было спасено 6 750 взрослых сосен, сэкономлено 155 тысяч кубометров воды или 155 триллионов литров, миллион кВт электроэнергии, не сожжен кислород, достаточный для 20 тысяч человек, и предотвращен выброс 1150 тонн СО2.
Сегодня часто приходится слышать о загрязнении окружающей среды и экологических проблемах на разных уголках нашей планеты. Перед всем человечеством встала большая проблема – остановить дальнейшее загрязнение нашей планеты и принять срочные меры по охране природы и окружающей среды. А все это начинается с малого: нам всем, государствам и каждому жителю нашей планеты, и взрослым и детям, нужно постараться сделать окружающую местность чище и благоустроеннее.
В решении данной проблемы играет огромную роль воспитанность каждого человека, передающаяся из поколения в поколение.
Именно с этой целью я предлагаю рассмотреть экологические задачи.
Математика является одним из предметов, который связан с экологией и эти науки тесно переплетаются. Экологизация математики дает возможность проследить процесс развития человеческих знаний во времени и пространстве. В связи с этим актуальность данного исследования не вызывает сомнения.
Предлагаю решить задачи, связанные с бережным отношением к нашей природе.
Математические задачи на тему
экологии и охраны окружающей среды
№1
Дом площадью 48м2 и высотой 3 м во время весеннего паводка был заполнен водой. Сколько кубических метров воды в доме?
№2
В мире ежегодно добывается 1600 млн.м3 древесины, около 20 % всей древесины идет на топливо. Сколько кубических метров древесины ежегодно сжигается?
№3
Одним из способов защиты окружающей среды является рассеивание вредных веществ с помощью строительства высоких труб. Известно, что дымовая труба высотой 100 м дает возможность рассеивать вредные вещества в радиусе 20м. Определить радиус рассеивания веществ, если высота трубы а) 50м, б) 80м.
№4
Из 1 м3 древесины получается 70кг бумаги. Сколько кубических метров древесины сэкономит 1000кг макулатуры?
№5
20 кг макулатуры сохраняет одно крупное дерево, а 1т макулатуры сберегает 0.5га леса среднего возраста. Определите количество леса, который можно сохранить, собрав 20 тонн макулатуры, 50 тонн макулатуры, 100 тонн макулатуры.
№6
Каждая мышь за год затаскивает в свою нору около 1кг зерна. А сова за год уничтожает 1000 мышей. Сколько килограммов зерна сберегут за год две совы?
№7
Пчела с миллиона цветков собирает 80кг мёда. Она за день садится на 10 тысяч цветков. Сколько граммов мёда собирает пчела за день?
№8
Выясните, какое количество речной воды мы теряем ежегодно, если известно, что в год мы сбрасываем в водоемы около 28 км3 неочищенных сточных вод, а 1 км3этих вод делает непригодной к употреблению 60 км3 вод.
№9
Подсчитано, что каждый легковой автомобиль при среднем годовом пробеге 15 тыс.км выдыхает 250кг углекислого газа, 93кг углеводорода, 27 кг окислов азота. Подсчитайте количество выделяемых за год в атмосферу веществ в нашем районе, учитывая, что в г. Навашино около 8000 автомобилей.
№10
Площадь города 10,8 тыс.га. Парки, бульвары, скверы занимают
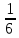часть этой площади. Сколько квадратных метров зеленых насаждений приходится на человека, если считать, что в городе 800000 жителей?№11
В мире в наши дни одна из самых острых проблем - нехватка чистой воды. Айсберг-это крупные обломки ледников, спускающихся с суши к морю. Айсберг представляет собой своеобразное хранилище пресной воды. Вычислить потребность воды на 1 человека в сутки, если ледяная гора толщиной 150м, длинной 2 км и шириной полкилометра содержит в себе столько пресной воды очень хорошего количества, которой бы хватило гигантскому городу Москве с населением 10 млн. человек на целый месяц, если плотность воды β 1000кг/м ?
Из 2 тонн макулатуры можно изготовить столько новой бумаги, сколько из 17 больших деревьев. Сколько можно сохранить деревьев, собрав 10 т макулатуры?
№12
Во время аварийных разливов нефти в мире гибнет около 1.000.000 водоплавающих птиц в год. Сколько птиц может погибнуть за 5 лет?
№13
В сутки через легкие человека проходят около 10000 литров воздуха. Сколько литров воздуха пропускают и очищают легкие за 1 неделю, за 1 месяц, 1год? Что мы называем «зелеными легкими» Земли?№32
Известно, что убытки от выбросов в атмосферу 1 тонны окиси углерода оцениваются от 100 до 500 тенге, 1 тонны нетоксичной пыли – от 450 до 225 тенге. Подсчитайте убытки нашей страны от загрязнения пылью атмосферы, если в 2000 г. ее было выброшено 1 млн. тонн.
№14
Ежегодно в морскую воду выливается около 10 млн.тонн отходов нефти. Если каждый литр отхода нефти загрязняет 1 куб. метров чистой воды, то, сколько тонн воды загрязняют отходы нефть за год?
Я провела свои расчеты выхлопа вредных веществ в г.Навашино, просчитав количество автомащин, проехавших за определенный промежуток времени в районе магазина «Кормилец». Данные приведены в таблице:
. Выводы.
В начале работы я хотела выяснить, может ли математика помочь в решении экологических проблем. Да может. На основе математических вычислений, люди делают выводы о том какую пользу или вред мы наносим природе.
Список использованной литературы
К. Ванов «Математика» 5-класс.
Ш. Карбаева «Естественные и математические науки в современном мире».
Е. Бурмистрова «Использование экологических задач на уроках математики».
Интернет –ресурсы.